背景イメージの変更と、それに伴う見出しやボックスの調整
背景イメージを切り替えても、XPLに薄い色線の枠が必要という結論
– – – – – – – – – – – – – – – – – – – – – – – – –
平均算を学習する中学受験生の方、「面積図が難しそう」「面倒くさい」と思っていませんか？
実は、正しい書き方を少し練習すれば同じ解き方で多くの問題は解けてしまうんですよ。
この記事では東大卒講師歴20年の図解講師「そうちゃ」が平均算の面積図の書き方を分かりやすく説明します。
記事を読みながらすれば平均算がだんだん得意になっていきますよ！
目次の好きなところをクリックするとジャンプできます！
いろいろな平均算
爽茶最後のテスト
何回かテストを受けて最後にもう一回テストを受けるような問題です。使う式はこちら
合計点数＝前回までの合計+最後の点数
=(前回までの平均×前回までの回数)+最後の点数
公式の使い方・図の書き方
一番簡単な問題で公式と図を使う練習
1-1:最後のテストの面積図
解説
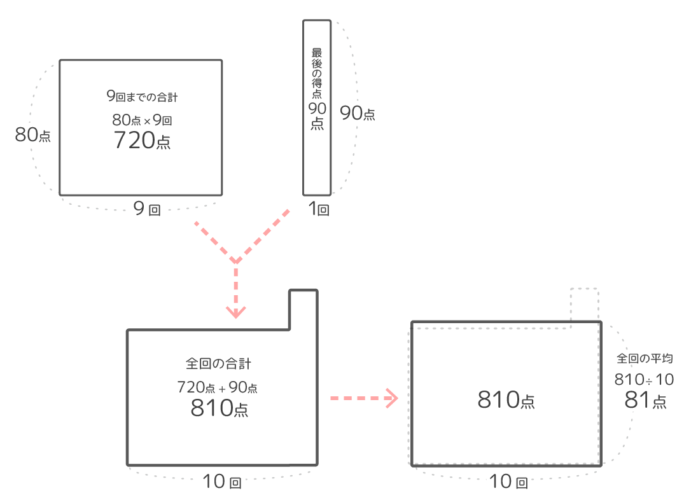
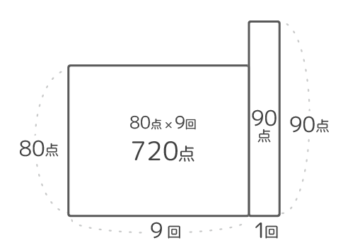
今までの回数と平均から80×9=720の長方形の面積図を書き(図1)。右端に最後のテスト(1×90の長方形)をとりつけます(図2)。この時の合計は80×9+90×1=810点になっています。
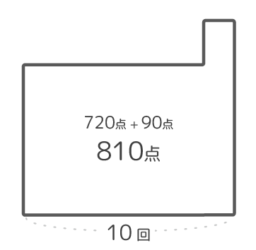
平らにならした高さが全回の平均で、810÷10で81点です。(図3)。
→→→
ならす
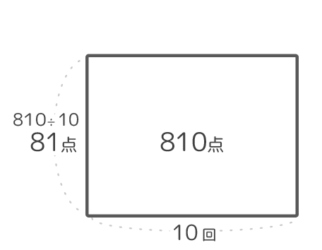
図の書き方の全体像を示します。
実際には最後の絵を書けばOK
難しい問題では、この図が約に立ちます。
簡単な問題
次のような回数が分かっている場合は図を書かなくても解けます。
1-1:サブタイトル
解説
五回全部の合計から四回目までの合計を引いたものが最後の点数です。
四回目までの合計点は70×4＝280点、五回全部の合計点は75×５＝375点なので、375－280＝95点が五回目のテストの点数と分かる。
図にするとこういう感じですね。
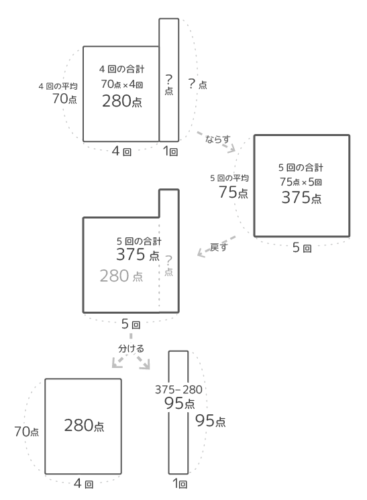
デコボコを一回ならして合計を出してから
もう一度デコボコに戻して
さらにもとの２つの面積図に分けています。
応用問題
次のように、回数が分からない場合は2つの面積図を重ねて解きます。「等しい面積を重ねると、はみ出た部分が等しくなる」のを利用します(詳しい説明は「面積図の重なり」を見て下さい。
1-1:サブタイトル
解説
今までのテストと最後のテストをくっつけた面積図を平らにならします(図1)
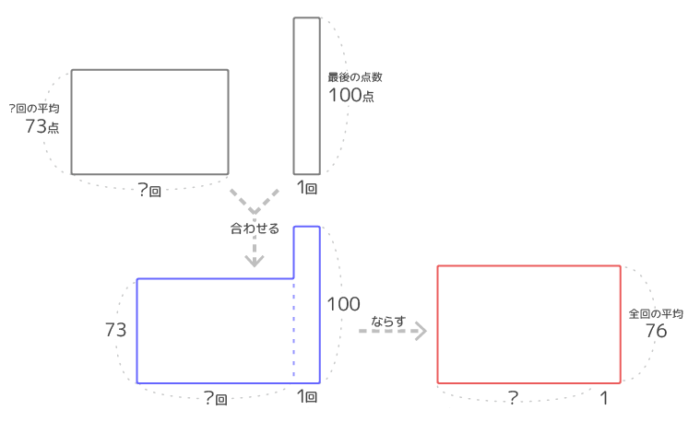
いつものパターンです
「ならす」前の凸凹の青い面積図と「ならした」後の赤い長方形の面積図を重ねると、2つの図は面積が等しいので「はみ出た部分(A,B)」の面積が等しくなります(図2)。
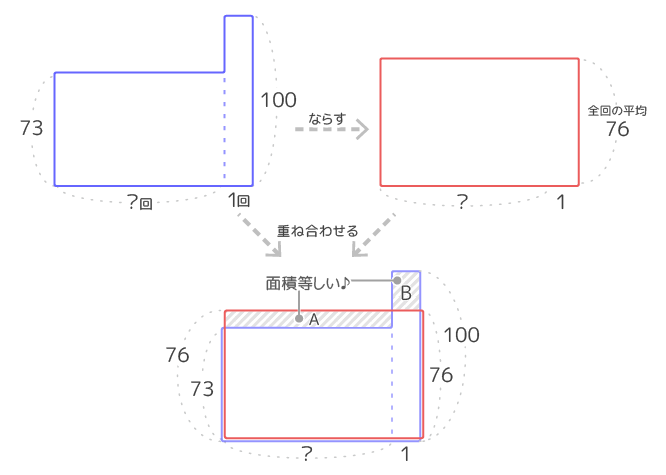
AとBは面積が等しくなる
Bはタテ24ヨコ1なので面積が1×24=24になり、Aの面積は同じく24でタテは3なのでヨコは24÷3=8と分かります。(図3)
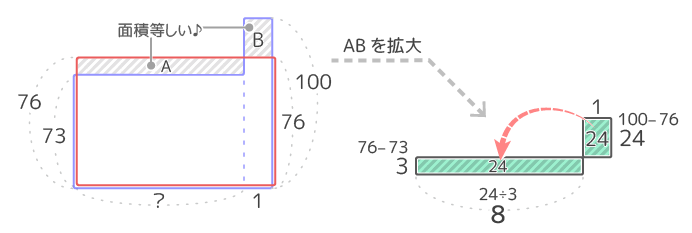
?が分かりました。
図の?=8なので、テストは全部で8+1=9回になります。
確認テスト(1)
何回かテストを受けて平均84点だったが、最後のテストで60点をとってしまい、全体の平均点が80点に下がってしまった。全部で何回テストを受けたか
→( 面積図を重ねて、等しい長方形を比べると、？×(84-80)=1×(80-60)なので、?=5回と分かる。テストは全部で6回 )
2つのグループ
クラスを男子と女子に、受験者を合格者と不合格者に、というように、集団を2つのグループに分け、集団全体とそれぞれグループの平均の関係を考える問題です。
公式/図の書き方
●グループAの合計=Aの平均×Aの人数
●グループBの合計=Bの平均×Bの人数
●全体の合計
=全体の平均×全体の人数(A+B)
=グループAの合計+グループBの合計
例題を解いてみます
1-1:2つのグループ(基本)
実際には最後の図を書けばOK
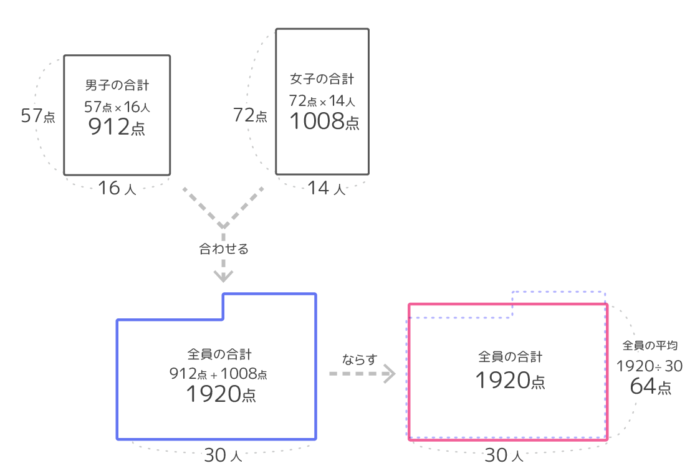
クラス全体の合計点=男子の合計点+女子の合計点です。男子の合計点＝57×16=912点、女子の合計点＝72×14=1008点なので、全体の合計点は912+1008=1920点と分かります(図1)
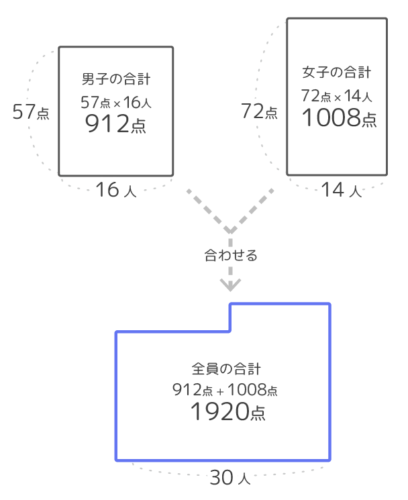
クラスの平均＝クラス全体の合計÷クラスの人数です。全体の合計＝1920、人数は16+14=30人なので、クラスの平均=1920÷30=64点です(図2)。
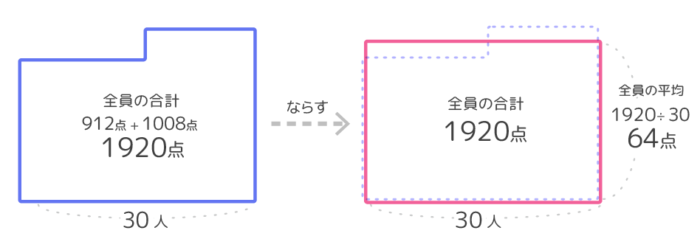
基本問題
人数や平均点が詳しく分かっている場合は面積図を使わなくても公式だけで解けることもあります。
2-1:2つのグループ(基本)
解説
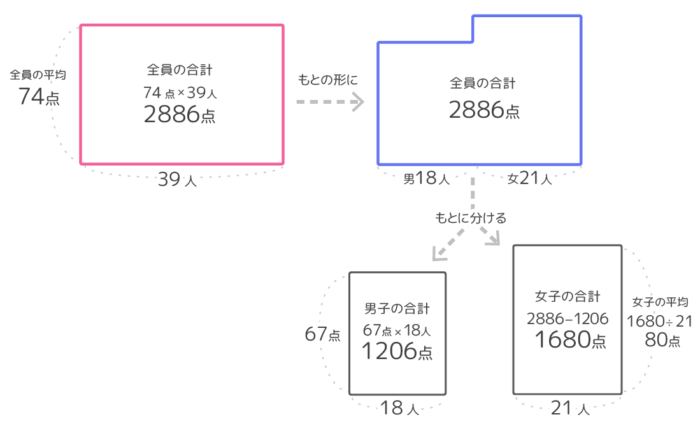
クラス全体の合計=(18+21)×74=2886点、男子の合計=18×67=1206点です。
そして女子の合計=全体の合計2886-男子の合計1206=1680なので、女子の平均は1680÷21=80点です。
さっきの問題と逆向きになっている。
確認テスト(2021.8.20作成中)
応用問題
数値が少なく、計算だけでは解けないな…と感じたらすぐに「重ね合わせ図」を書きます。
2-2-1:2つのグループ(応用)
クラス全体の合計点=45×75=3375点なので、男女別の面積図をあわせたL字形の面積も3375点。
女子の高い部分は縦9横20なので面積は9×20=180点なので、残りの長方形の面積は3375-180=3195点
この長方形は横が45で縦が男子の平均点なので、男子の平均点は3195÷45=71点と分かる。
女子の平均は71+9で80点
さらに具体的な得点が書いてない問題もあります。
2-2-2:2つのグループ(応用)
解説
まず大きさはテキトーで良いので不合格者の面積図と合格者の面積図を合わせた図(青)とならした図(赤)を書きます。この二つの面積は当然同じです。
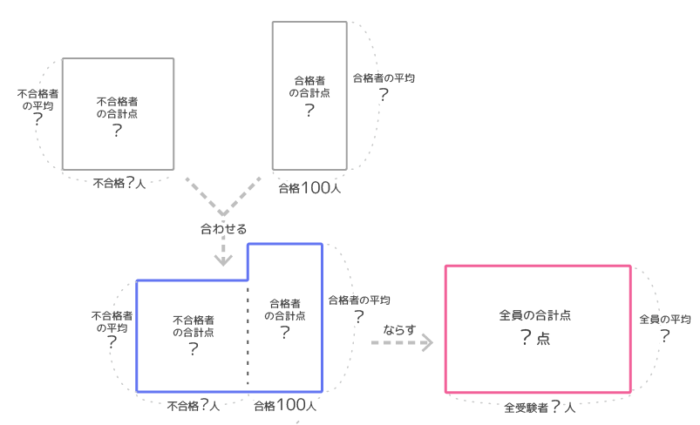
赤と青の面積は等しい
次に2つの面積図が重なった「重ね合わせ図」を作ります(図2)。等しい面積を重ねたので、はみ出たAとBの面積(斜線部分)は等しくなります。
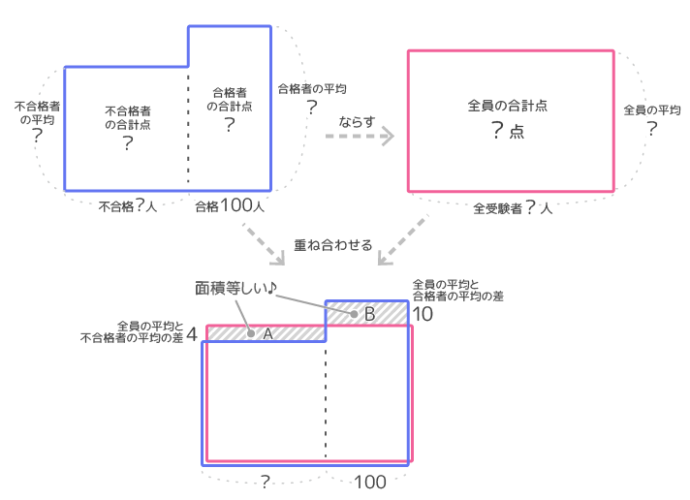
合格者の平均点は受験者全員の平均点より10点高いのでBのタテは10、不合格者の平均が合格者より14点低いのでAのタテは14-10=4です。また合格者の人数が100人なのでBのヨコは100です(図3)。
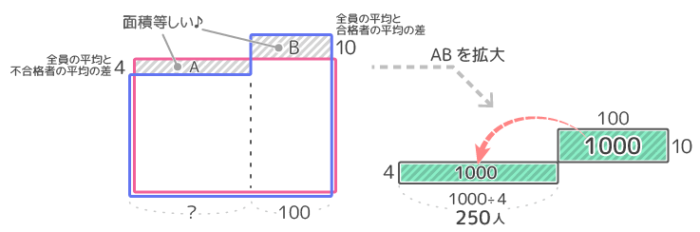
不合格者の人数が分かります
これでBの面積は10×100=1000と分かり、Aの面積も1000です。Aのタテが4なのでヨコは100÷4=250と分かります！これが不合格者の人数です(結局、平均点そのものは最後まで分かりません)。
以上より受験者の人数は、合格者100人+不合格者250人=350人です。
確認テスト(2021.8.20作成中)
段階式の価格
例えば「ある印刷工場では、ポスターを印刷してもらうのに枚数によって値段が変わります。10枚までは1枚○円、11枚以上30枚までは1枚●円、31枚以上は1枚◉円で印刷してもらえます。1枚あたりの値段が◆円以下になるには何枚以上印刷してもらう必要がありますか？」という問題です。
上で見た「2つのグループ」の問題のグループ数が3つ・4つになったような問題です。
(2020.2.17作成中)
度数分布表
表を読み取って解く次のような問題です。
度数分布表の使い方
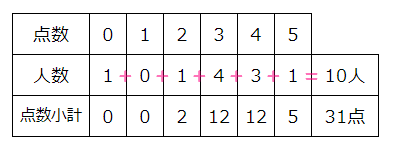
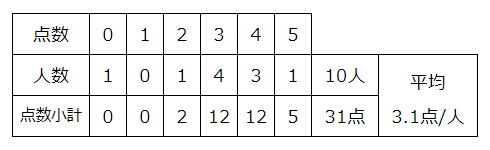
0点から5点までの点数がつくゲームを何人かでプレイした時の点数と人数を表にします(図1)
右から2列目は「4点をとった人数が3人」をあらわしています。
右から2列目は「4点を取ったのは3人」を意味する
この表を使って平均点を出してみましょう。
平均=合計÷人数なので、まず合計を求めます。
右から2列目の4点をとった3人の合計点(小計)は4×3=12点です。これを新しく作った三段目に書き込みます(図2)。同じように三段目を全て計算して、これらを合計すると全員の合計得点(総計)が31点と分かります！
右から2列目の3人の小計は4×3=12点
列ごとの小計を合わせると全員の合計が出る
人数の合計は二段目を合計すれば10人と分かります(図4)。
二段目を合わせると人数の合計が出る
結局、平均点は合計31÷人数10=3.1点と分かります(図5)。
合計点(31)÷人数(10)で平均点(3.1)が出る
基本問題(空欄1個)
次の様に空欄が1個の問題は簡単です。
(2020.2.25作成中)
応用問題(空欄2個)
次のような空欄が2つ以上ある問題は、つるかめ算で解きます。
「下の表は」
(2020.2.25作成中)
その他の応用問題
●単元学習中の小4・小5には定評のある「算数の基本問題(小5)」(日能研)
●サッと復習したい小6受験生には「算数ベストチェック」(日能研)
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評！
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ