「植木算って何?どうやるの?」「中学受験するならやっておいた方がいいの?」という小学三年生や「植木算が意外と難しい…」とお悩みの保護者の方へ。
植木算は受験算数の最初の方に出てくる単元ですが、実は結構難しいのです…なぜなら、植木算では「木」ではなく「間」の計算もしないと答えがでないので、「間」の計算と「木」の計算をまとめて理解しないといけないから。意外と「大きな」単元なのです
でも大丈夫!東大卒講師歴25年の図解講師「そうちゃ」が植木算の基本3パターンから応用問題まで全てを分かりやすく図解します。この記事を読んで真似すれば、あなたは「植木算博士」ですよ♪
目次をクリックするとジャンプできます。また最後に無料プリントがあるのでダウンロードしてご利用下さい。
植木算と学習方法
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
最初に植木算の学び方について軽く触れておきます♪植木算とは
「植木算」とは、ある距離の道に等間隔に木を植えていった時に木が何本必要になるか、などを求める問題です。
道の端にも木を植えるか、道が池などのまわりを一周するとどうなるか、など条件の違いでいくつかのパターンがあります。
この植木算を学ぶ際に意識してほしいことがあります。
植木算の学習のコツ
大事なのは「木」よりも「間」
まっすぐな道に植える植木算の図を見て下さい。
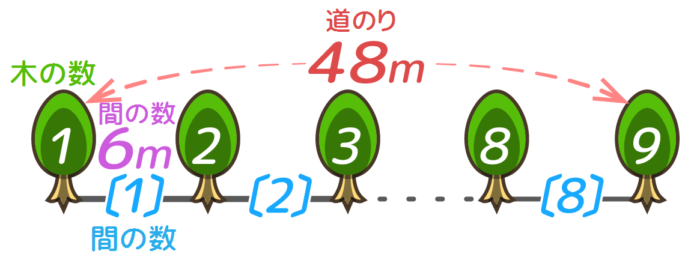
4種類の数字が登場します
「木の数」だけでなく「間(あいだ)の数」が書いてあるのに気づきます。
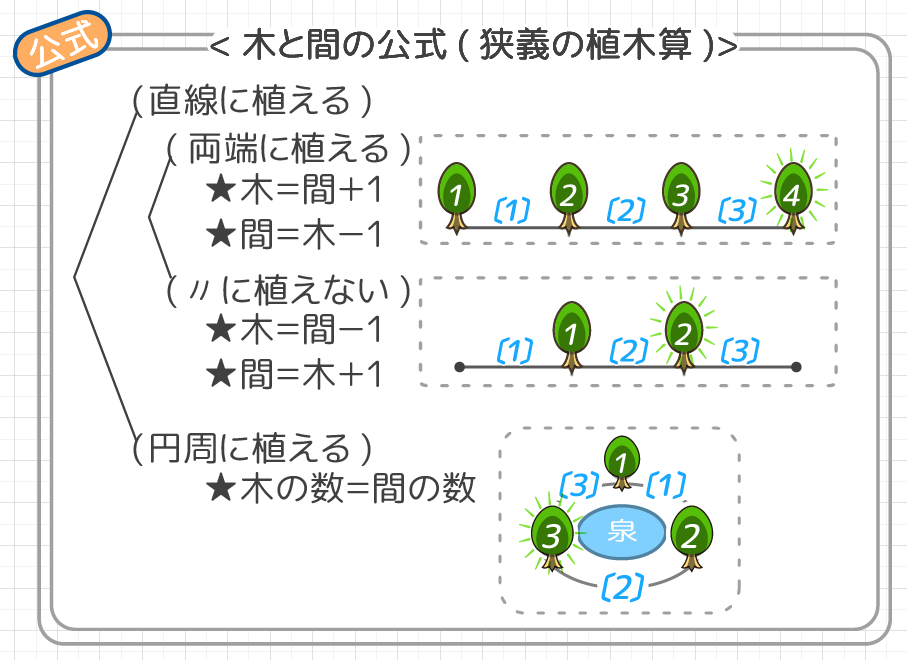
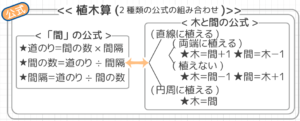
植木算は「間の公式」と「間の数と木の数」の2つの公式を組み合わせて解きます。
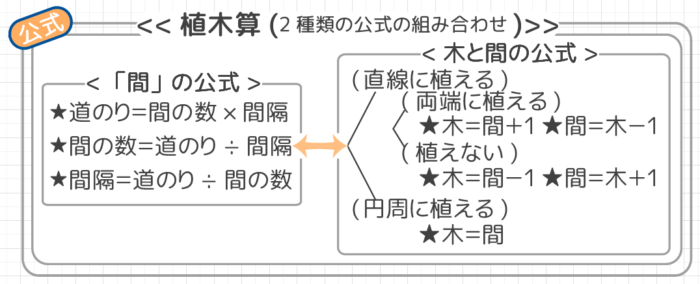
しかも、かけ算わり算など計算を主に行うのは「間の公式」の方です。
つまり「木」よりも「間」の方が重要です!
「間の数→木の数」の順に学ぶ
ですから、「植木算」を学ぶ際は、まず「間の公式」次に「木(の数)と間(の数)の関係」という2ステップで学ぶと分かりやすいです。
(ちなみに、お子さんや生徒さんに教える方法を詳しく知りたい人は「植木算の教え方」を見て下さい)
間(あいだ)の数
上で書いたように「植木算」では「間の数」の計算がメインなので、植木算の前に「間の数」の公式を使えるようにしておきます。
間の公式
ある道を等しい「間かく」で区切ります。このとき、「道のり」「間の数」「間かく」は次のような関係(公式)になります。
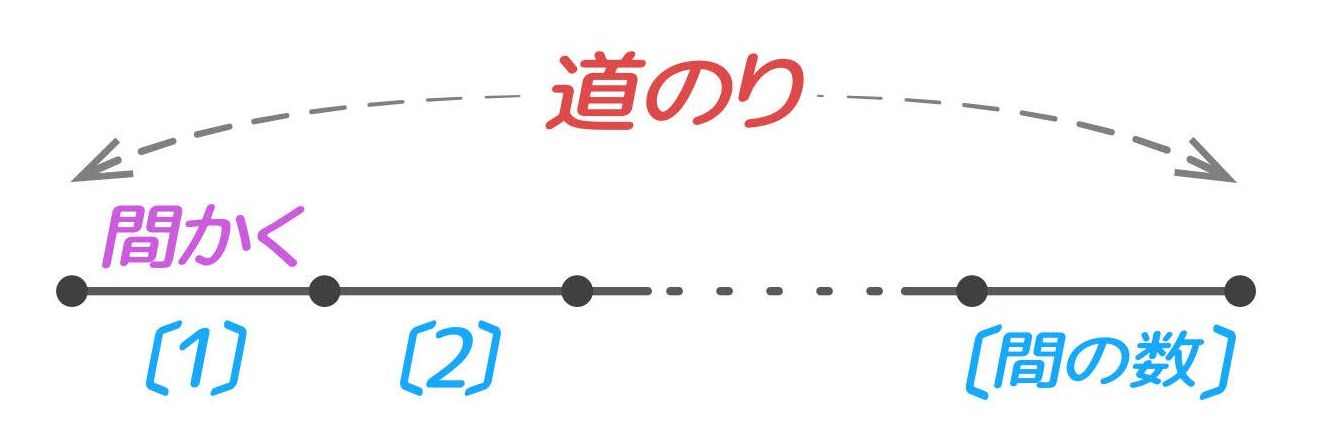
(間の公式)
❶道のり(m)=間かく(mおき)×間の数(個)
❷間の数(個)=道のり(m)÷間かく(mおき)
❸間かく(mおき)=道のり(m)÷間の数(個)
確認テスト
ためしに問題をどうぞ。
10mの道を2mの間かくで区切ると間の数はいくつか?
→( 間の数=10(道のり)÷2(間かく)=5個 )
3mの間かく7個に区切られている道の長さは?
→( 道のり=3(間かく)×7(間の数)=21m )
54mの道を9個に区切ると間かくの長さは?
→( 間かく=54(道のり)÷9(間の数)=6m )
もっと詳しい説明を読みたい人は参考記事「間の数」を見てください。
プリント
記事の一番下でプリントをダウンロードできます。


次は「植木算の基本3パターン」です。
植木算の基本3パターン
3種類の木の植え方
木の植え方によって「間と木の関係」が変わります。(よく「植木算の公式」と言われているのがコレです)
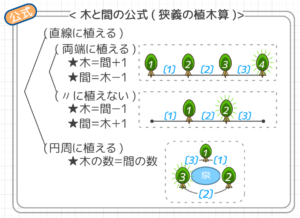
3種類の植え方「A:直線上に両端にも植える」「B:直線上に両端以外に植える」「C:円の周りに植える」この3つが基本パターンです。
問題を読んだら「A:直線(両端あり)」「B:直線(両端なし)」「C:円周」のどれかを考えましょう。
図の書き方
問題文を整理して考えやすくするために、「木の数」はもちろん「間の数」「道のり」「間かく」の合計4種類の数字を書きましょう。木が多いときは、途中を省略して最後の2つを書けば十分です。

4種類の数字を書きましょう
では基本3パターンを順に説明します。
A:直線(両端あり)
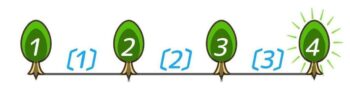
真っ直ぐな道のような直線上に、端から端まで木を植えると、木は間より1つ多く(間は木より1つ少なく)なる。
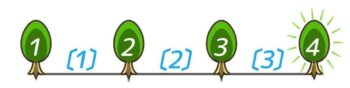
この「木の数が間の数より1つ多い(木=間+1,間=木-1)」と「間の公式」を組み合わせて問題を解きます。

❶道のり(m)=間かく(mおき)×間の数(個)
❷間の数(個)=道のり(m)÷間かく(mおき)
❸間かく(mおき)=道のり(m)÷間の数(個)
例えば「15mの道の端から端までに3mおきに木を植える」場合、
①まず「間の公式」で間の数を 15÷3=5 と計算し
②次に「木と間の公式:直線の両端に植える」で木の数を間の数5+1=6本と計算します。
確認テストをどうぞ。
20mの道の端から端までに2mおきに木を植えると全部で何本か
→( 間の数=20÷2=10個。両端に植えるので木の数が多く、10+1=11本 )
木を8mの間隔で道の両端にも植えたら10本必要。道の長さは何mか?
→( 両端に植えるので木の数が多く、間の数=10-1=9個。道のり=8×9=72m )
60mの道の端から端まで等間隔に11本の木を植える。何mおきに植えればよいか
→( 両端に植えるので木の数が多く、間の数=11-1=10個。間かく=60÷10=6m )
B:直線(両端なし)
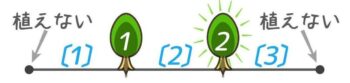
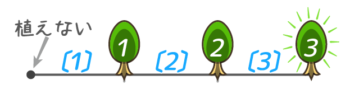
直線の両端(道の始点と終点)に植えない場合、木の数は間の数より1つ少なくなる。
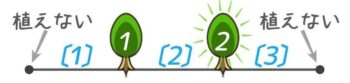
この「木の数が間の数より1つ少ない(木=間-1,間=木+1)」と「間の公式」を組み合わせて問題を解きます。
例えば「15mの道に3mおきに木を植えるが端には木を植えない」場合、
①まず「間の公式」で間の数を 15÷3=5 と計算し
②次に「木と間の公式:直線の両端に植えない」で木の数を間の数5-1=4本と計算します。
確認テストをどうぞ。
20mの道の始点と終点以外に2mおきに木を植えると全部で何本になるか
→( 間の数=20÷2=10個。両端に植えないので木の数が1本少なく、10-1=9本 )
まっすぐな道の両端を除いて8mの間隔で電柱を立てたら10本必要だった。道の長さは何mか?
→( 両端に植えないので木の数が1本少ない=間の数が1本多く10+1=11個。道のり=8×11=88m )
18mの道に8本の木を植える。両端には植えない時、何mおきに植えればよいか
→( 両端に植えないので間の数が多く8+1=9個。間かく=18÷9=2m )
分かりましたか?直線上に植える2つの場合をまとめるとこうなります。
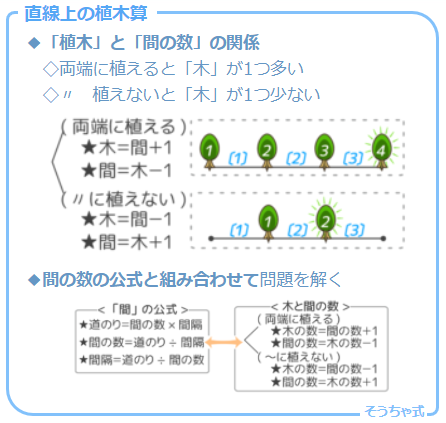
「両端」と「両側」の違い
道を横から見たときの「はじめと終わり」を「両端」と呼びます。一方「両側」は道の上にいる人から見て「左右両側」です。
問題に「両側」と書いていない場合は「片側」つまり「左右のどちらか」にだけ木が並んでいます。
テストで確認してみましょう♪
100mの道の両側に5mおきに旗を立てる。スタートとゴールには旗ではなくゲートを立てるとき、旗は全部で何本必要か?
→( まず片側を考えると、間の数は100÷5=20個、両端に立てないので旗の数は19個。これが左右両側にあるので旗は全部で19×2=38個 )
もっと詳しい説明を読みたい人は参考記事「直線上にならべた植木」を見てください。
問題&解答プリント
記事の一番下でプリントをダウンロードできます。


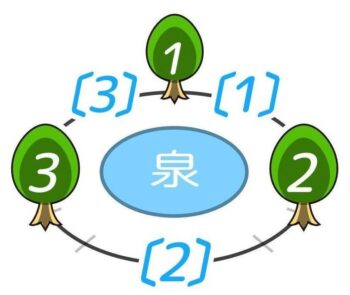
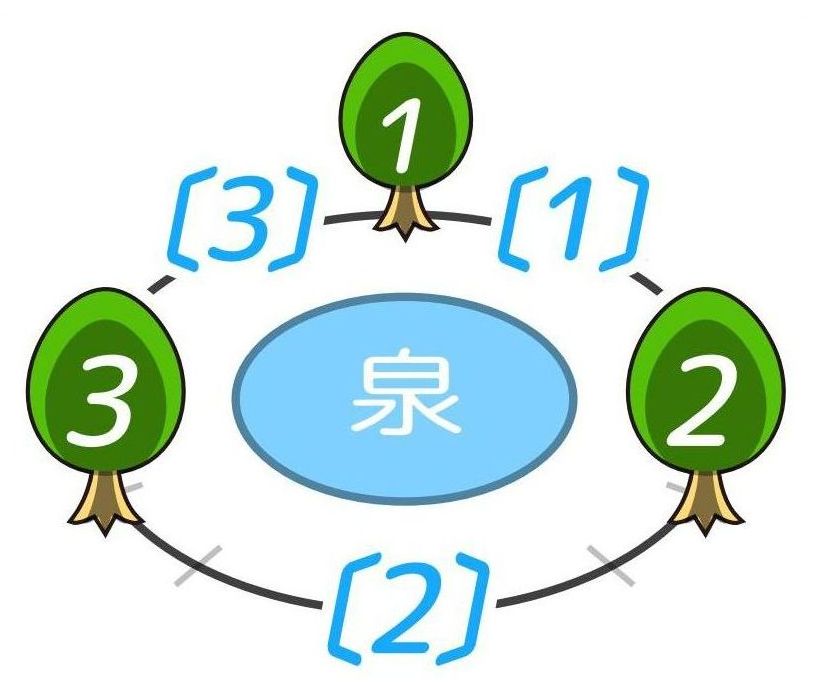
C:円周上の植木
木を円周上に植える場合、間の数と木の数は同じです。
「間の公式」だけを使えば解けるので単純ですね!
試しに問題を解いてみましょう。
池の周りに8本の木を等間隔に植えたらちょうど3mおきになった。一周は何mか?
→( 間隔は木と同じく8個。道のり=3×8=24m )
一周48mの円周上の道に4mおきに木を植えるのに何本必要か
→( 間かくは48÷4=12個。木の数も同じく12個 )
さらに詳しい説明を読みたい人は参考記事「円周上にならべた植木」を見てください。
問題&解答プリント
記事の一番下でプリントをダウンロードできます。


(直線の片端だけ植える)
基本パターンには入れませんが、直線の一方の端だけに植える場合、木の数と間の数は等しくなります。
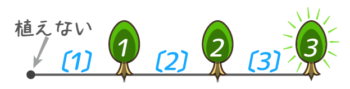
つまり、円周上に並べるのと同じく「間の公式」だけで解けます。便利なので憶えておくとオトクです♪(応用問題(不定形線上の植木算)で特に便利)
★ここまで来ると、3パターンを公式のように憶えるだけでなく、問題文を読んだら簡単な図を書いて状況を理解するのが大切です。
基本パターン総合問題
ここまでの全知識を総動員して解きましょう。
解答プリント
記事の一番下でプリントをダウンロードできます。

 爽茶
爽茶植木算の応用問題
ここからは、植木算の応用問題を紹介します。
不定形植木算
運動会などのイベントで「人文字」を作ることがありますね。アレの立っている人数を求めるような問題です。
円と線に分割する
例えば1mおきに人が立って図のような人文字(頭は周長が12m,首の長さ1m,腕10m,胴4m,脚12m)を作るときに何人が必要か?

カタチが複雑なので、単純な「線」や「円」に分けてみます。その際、線の端に人が立つかどうかを考えるのが大切です。
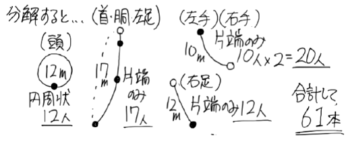
線の端は木が植えてある場合は●で、植えてない場合は○で示してあります。
例えば、首の付け根の部分に立つ人は「頭」として数えて「首・胴・左足」の上端には人が立っていないとします。
これで頭の部分は「円周上」それ以外は「片端のみ」に分解でき、これら2つのパターンは「木の数=間の数」なので、道のり÷間かくで間の数を出せば、それが人の数になります。
線の長さが12+17+10×2+12=61mで間かくが1mなので、間の数=61÷1=61個、人(木)の数も61人ですね。
二次植木算
木と木の間に、さらに木を植える場合です。まず基本の植木算で「間かく」を出した後、間の中で二回目の植木算をおこないます。
ポイントは、二回目の植木算が「両端に植えない」パターンになることです。
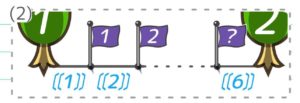
◆木と木の間にさらに木を植える場合
→「両端に植えない」パターンになる
→「木」は間より1少なくなる
(例)木の間12mにさらに2m間かくで旗を立てる
→間の数=12÷2=6個。旗の数=6-1=5本
→それぞれの間には5本の旗が立つ
ためしに解いてみましょう♪
48mの道の端から端まで16mおきに柱を立て、柱の間には2mおきに木を植える。木は全部で何本か
→( 柱の間が48÷16=3個できて、一つの間がさらに16÷2=8個に区切られて、両端に植えないパターンなので7本の木が植えられる。木の数は合計で7×3=21本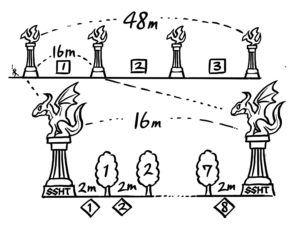 )
)
詳しい説明を読みたい人は参考記事「二次植木算」を見てください。
問題&解答プリント
記事の一番下でプリントをダウンロードできます。
面の植木算
縦・横に木を植える場合です。タテ・ヨコの本数を出してそれをかけ合わせます。
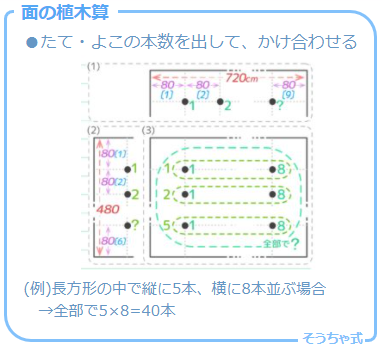
さらに詳しい説明を読みたい人は参考記事「面の植木算」を見てください。
問題&解答プリント
記事の一番下でプリントをダウンロードできます。
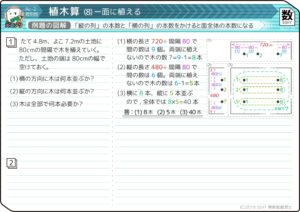
番号付き植木
木に番号がついている問題です。計算は2つの木の番号の差=「番差」で行うのがコツです。

確認テストを解いてみましょう。
98mの道の端から端まで等間隔に50本の木が植えてあり1番から50番までの番号がふってある。
14番の木と62m離れているのは何番の木か?
→( まず間隔を出すと、両端に植えるので木が間より多く、間は全部で50-1=49個で間隔は98÷49=2m )
→( 62m離れた木までの間の数は62÷2=31=番差なので、14+31=45番の木 )
10番の木と68番の木は何m離れているか?
→( 2つの木の番差は68-10=58=間の数なので、道のり=2×58=116m )
問題&解答プリント
記事の一番下でプリントをダウンロードできます。


幅がある植木算
1mの幅がある花壇を3mおきに設置するように幅があるものを一定間隔で置いていく問題です。
(例題1:道幅が分からない)
1m幅の花壇を3mおきに10個設置すると、花壇の端から端まで何mになるか?
花壇が10個で1×10=10m、間の数は「両端に植えるパターン」なので10-1=9個で、間の長さの合計は3×9=27mです。
花壇と間の数の長さの合計は10m+27m=37mです。
(例題2:間かくが分からない)25mの道の端から端まで幅1mの花壇を5個ひとしい間隔に並べたい。何mおきに並べれば良いか?
花壇5個の幅の合計は1×5=5m。道の長さ25-5=20mが間の長さの合計になる。
間の数は5-1=4個なので、一つの間は20÷4=5mです。
(例題3:花壇の幅が分からない)
(例題3:花壇の個数が分からない)
時間の植木算
ここまでは線・面などの「空間」を区切ってきましたが、「時間」を区切るのも同じように考えられます。
基本
単純なものは、例えば「タイマーの音が鳴る」のように、一定時間おきにイベントが起きる問題です。
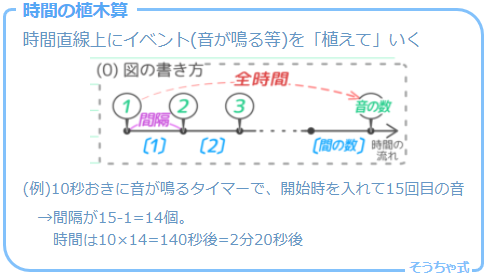
二次時間植木算
上で説明した「二次植木算」を時間の流れの中で行う問題です。
例えば、1時間おきに音楽が流れて音楽の間には10分お気にアラーム音が鳴る時計があって、朝7時に音楽が流れてから夕方5時までにアラーム音は何回鳴るか?
7時から5時までは17-7=10時間で、1時間の間かくは10÷1=10個ある。
そして、この1時間(60分)間かくの中にアラームの10分間かくは60÷10=6個で、両端に植えないパターンでアラームが鳴る回数は5回。
アラームが鳴る回数は全部で、5x10=50回です。
幅のある時間植木算
「幅のある植木算」と合わせると、50分授業を受けたら10分休憩する、のような作業の合間に休憩をはさむような問題になります。
さらに詳しい説明を読みたい人は「時間の植木算」を見てください。
図形をつなぐ問題
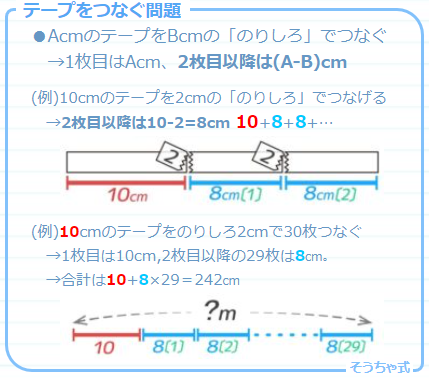
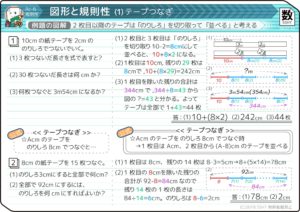
テープつなぎ
同じ長さの紙テープを同じ長さの「のりしろ」でつないでいく問題です。植木算ではなく等差数列風に解くのがラクです。
問題を解いてみましょう♪
12cmのテープを3cmの「のりしろ」で8枚つなぐと何cmになるか?
→( 2枚目からは12-3=9cmになり、これが8-1=7枚あるので、12+9×7=75cm )
上と同じテープとのりしろでつないだら111cmになった。何枚のテープをつないだか?
→( 111cmから1枚目をテープを除いた長さは111-12=99cmで、これは2枚目からのテープの99÷9=11枚分と分かる。テープは全部で1+11=12枚 )
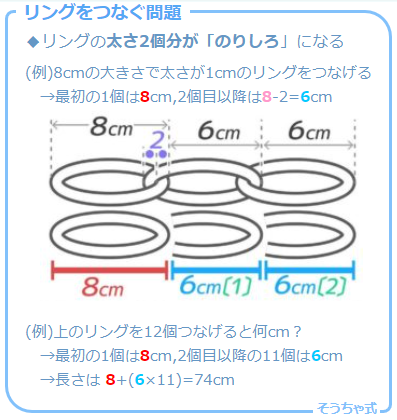
リングつなぎ
リングをつなぐ場合はリングの太さの2倍をのりしろと考えて同様に解きます。
問題を解いてみましょう♪
10cmの大きさで太さが5mmのリングを20個つなぐと何cmになるか?
→( 5mm×2=10mm=1cmがのりしろになるので、2個めからのリングの長さは10-1=9cmになり、これが20-1=19個あるので、全部で10+(9×19)=181cmになる。 )
さらに詳しい説明を読みたい人は参考記事「植木算の応用」内の「テープつなぎの問題」を見てください。
問題&解答プリント
記事の一番下でプリントをダウンロードできます。

プリントダウンロード
このサイトで使用した植木算プリント31枚以上をまとめてダウンロードできます♪
zipファイルの中に問題だけのPDFと解答だけのPDFが入っているのでご利用下さい。
著作権は放棄しておりません。無断転載引用はご遠慮下さい。
ダウンロードにはパスワードが必要です。こちらからDL登録すると自動返信メールでパスワードを受け取れます。
*「パスワードを入れてもダウンロードできない」という方はブラウザや使用機種を変えて再度お試し下さい
植木算のまとめは以上です。お疲れさまでした!
植木算は「規則性」という分野の二番目です。植木算を制覇した人は「数列」に進んでみましょう!また「方陣算」も同じ分野の応用です。
おすすめ教材
 爽茶
爽茶●植木算だけをたくさん解きたいなら「植木算」(サイパーシリーズ)
●受験算数を幅広く復習したい小4受験生には「算数の基本問題4年」(日能研)
●受験準備に特殊算を広く浅くまなびたい低学年には小4まで…和差センス(シグマベスト)
●本格的に受験算数全般を学びたいなら「中学入試 塾技100(算数)」
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ