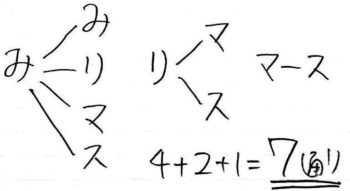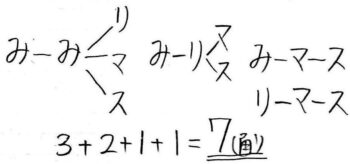●場合の数のまとめ(この記事)
●色玉の問題
●金額の問題
●経路・道順の問題
●地図の塗り分け問題
●試合数の問題
中学受験生で「場合の数」が苦手な方、あなたは「場合の数って色んな問題があって訳が分からない!」と悩んでいませんか?
実は、あなたの感じ方は正解です。「場合の数」は他の分野の問題と比べると、本当に色んな種類の問題・解き方があるんです…
しかし、安心して下さい!問題の種類はたくさんあっても、共通して使う公式は実は3~4個しかないんですよ!
だから、色んな問題の解き方をバラバラに覚えるのではなく、まずは基本公式をしっかり使えるようにして、それから「数字カード」などのタイプ別問題にいきましょう。
そして、それぞれの問題が「どの基本公式を使うのか」が分かるようにしていけば、解ける問題がどんどん増えていくのです。
この記事では東大卒講師歴20年の図解講師「そうちゃ」が基本公式の覚え方から応用問題での使い方までネット上で一番分かりやすく解説します!
記事を読んで公式を憶え、例題を真似して問題を解けば「場合の数」が苦手ではなくなっているでしょう。
この記事は長いので、目次をクリックして読みたい場所に飛んで下さい♪
場合の数の基本ルール
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
はじめに「場合の数」で必ず使う基本的なルールを説明します。基本ルールは2つだけ!(マジ)
2つのルール
場合の数には非常に多くの種類の問題があるが、使うルールは大きく分けてこの2つだけ!
●ならべ方(順列)
(例)〃リレーの選手を走る順に3人決める
●えらび方(組み合わせ)
(例)30人のクラスで掃除当番を3人決める
区別の方法
2つしかないとしても、どちらを使うのかをどうやって区別すればよいかが気になりますね?
この先を読み進めば分かりますが、気になる人は「開く」をクリック
基本的に「順番を気にするかしないか」で区別します
例えば、
数字カードを2枚引いて2ケタの整数を作る場合、「1」「2」と「2」「1」は違います。つまり順番を気にするので→ならべ方
一方、単に数字カードを2枚引く場合、「1」「2」と「2」「1」は同じです。つまり順番を気にしないので→えらび方の問題になります
順番でなく「位置」や「地位」でも同じです。
例えば、
「10人から1等・2等・3等の当選者を決める」場合、当たりくじに「1等」「2等」「3等」という地位があります→ならべ方
一方、「10人から当選者3人を決める」場合、当たりくじに差はありません→「えらび方」の問題になります
それでは2つのルールをみていきましょう
ならべ方
いくつかの物の順番を変える場合の数。
「全部ならべかえ」と「一部ならべかえ」がある。
全部を並べかえる
用意された物や人の全部を並べかえる場合の数
●N個全部を並べかえる
→N×(N-1)×(N-2)×…×1 通り
(例1)5個全部を並べかえる
→5×4×3×2×1=120 通り
確認テストをどうぞ
1-1-1:全部ならべかえ
解説
公式「N×(N-1)×(N-2)×…×1 通り」のNを3にして、3x2x1=6通り
これは1文字目,2文字目,3文字目の場合の数のかけ算で、樹形図を書いても同じ計算になる
解説
公式「N×(N-1)×(N-2)×…×1 通り」のNを4にするので、4x3x2x1=24通り
これは立つ位置を「ア」「イ」「ウ」「エ」としたときの場合の数のかけ算で、樹形図を書いても同じ計算になる
後半を省略して書く
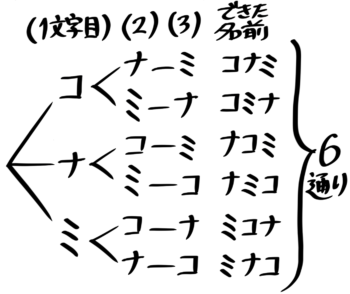
例えば「『コ』『ナ』『ミ』の3文字を並びかえて名前を考えると何通りあるか?」を考えます。
1文字目に使える文字は「コ」「ナ」「ミ」の3通り、1文字目に「コ」を選んだ場合2文字目は「ナ」「ミ」の2通り、1文字目に「コ」2文字目に「ナ」を選んだ場合3文字目は「ミ」の1通りになります。ここまでを図にするとこうなります
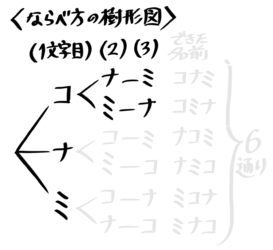
「コナミ」と「コミナ」の2通り
続けて最後まで書くと6通りと分かります
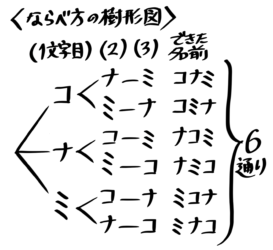
「ミ」にした場合もそれぞれ2通り
これを「並べ方の樹形図」と言います。上で書いた「えらび方の樹形図」と違って一つの大きな図になっているのが特徴です。

大きな1つの樹

だんだん小さくなっていく
樹がいくつか並んでいる
「並べ方の樹形図」を書くときは、項目(この場合は「1文字目」等)を必ず書きましょう
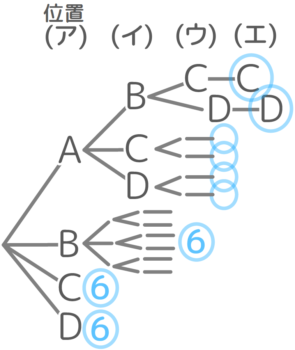
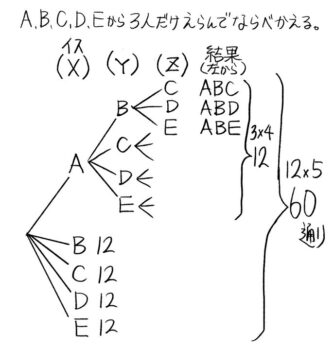
次に「横に並んだ4つのイスにABCD3人が座る場合の並び方は何通りあるか」考えます。イスにWXYZと名前をつけて、図を書いて調べるとこうなります。
((樹形図))
全部で24通りと分かりました。
数が多くなってくると全部書くのが難しくなるので、初めの方だけ丁寧に書き、同じ形が繰り返されるところは省略して数だけ書くと良いです。
図を書かずに計算で出すことも出来ます。
Wに座る人はABCDの4通り、Xに座る人はWに座った誰か以外の3人で3通り、Yに座る人はWXに座った二人以外の2人で2通り、Zに座るのは残った一人で1通りです。
いま出した「4通り」「3通り」「2通り」「1通り」をどうすれば樹形図で調べた答えである「24」通りになるでしょうか?
4×3×2×1=24 でかけ算ですね。つまりN個のもの全部を並べる場合の数は、N×(N-1)×(N-2)×…×1 で求めることができます。
もっと詳しい説明を見たい、いろんな問題を解きたい人は「場合の数の基本ルール」を見て下さい。
一部並び替え
用意された物から何個か選んで並べかえる場合の数です。
●N個からA個えらんで並べかえる
→N×(N-1)×…×(N-A+1) 通り
(例1)5個から2個えらんで並べかえる
w① ②
→5×4=60 通り
(例1)7個から3個えらんで並べかえる
w① ② ③
→7×6×5=210 通り
この公式は形を覚えるというよりも、数字が入った例から式を作れればOKです。
確認テストをどうぞ
1-1-2:一部ならべかえ
解説
5人から3人えらんで並べかえるので
w① ② ③
→5×4×3=60 通り
樹形図を書いても同じ結果になる
後半は省略するのがコツ
解説
20人から2人えらんで並べかえるので
w ① ②
→20×19=380 通り
このような単純な問題は樹形図を書かずに計算で出しても良い
例えば、6人の中から3人選んで3つのイスXYZに座ってもらいます。Xに座る人は6人の誰かで6通り、Yに座る人はXに座った誰か以外の5人で5通り、Zに座るのはXYに座った2人以外の4人で4通りです。
この数字をかけ算した 6×5×4=120通り が答えになります。
((樹形図))
もっと詳しい説明を見たい、いろんな問題を解きたい人は「場合の数の基本ルール」を見て下さい。
えらび方
何種類かの物から選ぶ場合の数。4年生まではこちらができるように
●N個から1個選ぶ→N通り
●N個から2個選ぶ→(N-1)+(N-2)+…+1 通り
●N個からM個選ぶ(裏技)
→N–M=2なら、2個選ぶ公式が使える
5–3=2なので、5個から2個選ぶのと同じ
→4+3+2+1=10通り
5年生以降はこちらを覚えておけば受験もOK
●N個から1個選ぶ→N通り
(例)5種類から1個選ぶ→5通り
●N個から2個選ぶ→N×(N-1)2 × 1
(例)5個から2個選ぶ→5 × 42 × 1=10通り
●N個から3個選ぶ→N×(N-1)×(N-2)3 × 2 × 1
(例)6個から3個選ぶ→6 × 5 × 43 × 2 × 1=20通り
●N個から4個選ぶ→N×(N-1)×(N-2)×(N-3)4 × 3 × 2 × 1
(例)10個から4個選ぶ→10× 9 × 8 × 7 4 × 3 × 2 × 1=210通り
●N個からM個選ぶ→N個から(N–M)個選ぶのと同じ
(例)100個から97個選ぶ→100個から(100–97)=3個選ぶのと同じ
テストで確認♪
1-2-1:えらび方
解説
10個から2個選ぶので、10 × 92 × 1=45通り
4年までの公式では、9+8+7+…+1=45(ちょっと面倒…)
解説
12個から8個選ぶ→12個から(12–8)=4個選ぶのと同じ
12個から4個選ぶ→12× 11 × 10 × 94 × 3 × 2 × 1=495通り
N個から1個選ぶ
当然、N通りあります。
(例)4種類の味のアイスから1種類選ぶ場合は4通りです。
N個から2個選ぶ
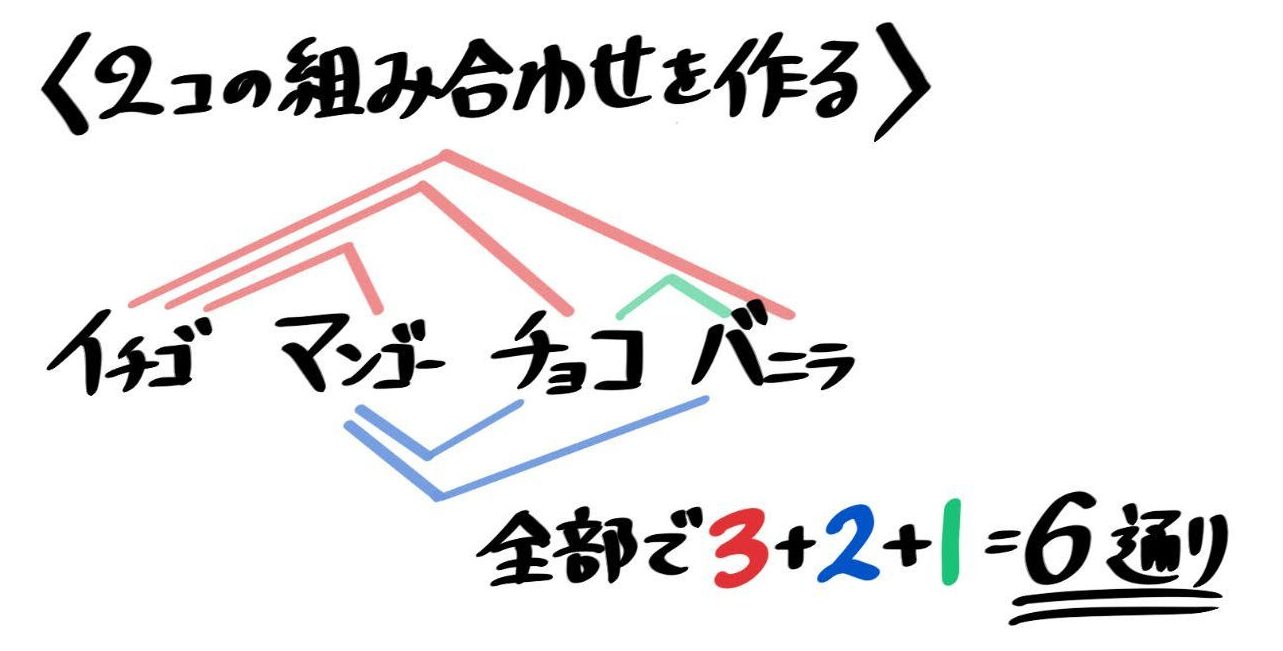
例えば「イチゴ・マンゴー・チョコ・バニラ4種類の味のアイスから2種類選ぶ場合の数はいくつ?」を考えます。
2個づつの「組み合わせ」を作っていきますが、この時「左→右」の順を必ず守って下さい。「イチゴ&マンゴー」はOKですが「マンゴー&イチゴ」はNGです。
これは、同じ組み合わせを2回数えてしまわないための工夫です。(「イチゴ&マンゴー」と「マンゴー&イチゴ」は同じ組み合わせなので2回数えるのは間違い)
図を書いて組み合わせを数えると、3+2+1=6通りと分かります。
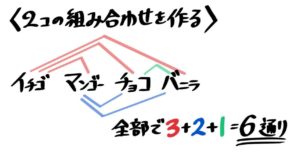
この組み合わせの作り方でOKなのですが、よく使う図は下のような図で「樹形図」と言います。内容は上の図と全く同じです。
「イチゴ・マンゴー・チョコ・バニラ」の頭文字をつなげて「イマチバ」「マチバ」「チバ」の順に書いていきます

こちらの方が書きやすいですね。
このような「だんだん小さくなっていくカタマリが横に並んでいる」図を「えらび方の樹形図」といいます。
今度は「イチゴ・マンゴー・チョコ・バニラ・ミント5種類から2個えらぶ場合」を考えます。
「イマチバミ」「マチバミ」「チバミ」「バミ」と書くと樹形図ができます

4+3+2+1=10通り
4+3+2+1=10通り になります。
公式化する♪
4種類から2種類選ぶと3+2+1=6通り
5種類から2種類選ぶと4+3+2+1=10通り なので
N個から2個選ぶ場合の数は、(N-1)+(N-2)+…+1 になると分かります。
●N個から2個選ぶ
→(N-1)+(N-2)+…+1 通り
(例1)5種類から2種類選ぶ
→4+3+2+1=10通り
(例2)10種類から2種類選ぶ
→9+8+7+…+3+2+1=45通り
N個から3個以上選ぶ
書き出す
2個選ぶ場合と同様に、樹形図を書いて出すことができます
例えば「イチゴ・マンゴー・チョコ・バニラ・ミント5種類から3個えらぶ場合」は、「イマチバミ」の順に3個セットで「イマチ」「イマバ」「イマミ」「イチバ」「イチミ」「イバミ」…と書いていきます。
から3個えらぶ
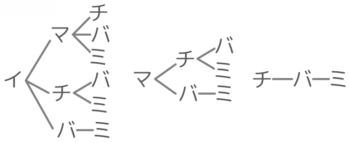
しかし、選ぶもとの数が増えると、樹形図を書くのは大変です。
裏技で出す
実は、先程の「5種類から3個選ぶ」のは選ばない方の2個を選ぶ、つまり「5種類から3個選ぶ」と同じなのです。


これは5個から選ぶときだけでなく、6個から選ぶのも7個から選ぶのでも同じになります。
例えば10個から8個選ぶ場合は、10個から2個選ぶのと同じで 9+8+7+…+1=45通り になります(少し面倒くさいですが…)
●N個から(N-2)個えらぶ場合
→N個から2個選ぶのと同じ
(例1)5個から3個選ぶ場合
→5個から2個選ぶのと同じ
4+3+2+1=10通り
(例2)10個から8個選ぶ場合
→10個から2個選ぶのと同じ
9+8+7+…+1=45通り
公式で出す
今の裏技を使えない場合や、3個に限らず、どういう場合にでも使える便利な公式です(公立では高校に習います)
●N個から2個選ぶ→N×(N-1)2 × 1
(例)5個から2個選ぶ→5 × 42 × 1
●N個から3個選ぶ→N×(N-1)×(N-2)3 × 2 × 1
(例)6個から3個選ぶ→6 × 5 × 43 × 2 × 1
●N個から4個選ぶ→N×(N-1)×(N-2)×(N-3)4 × 3 × 2 × 1
(例)10個から4個選ぶ→10× 9 × 8 × 7 4 × 3 × 2 × 1
この公式は受験学年(6年生)までには覚えましょう
もっと詳しい説明を見たい、いろんな問題を解きたい人は「場合の数の基本ルール」を見て下さい。
場合の数同士の関係(和と積の法則)
問題を解いていて場合の数が2つ出た場合に、2つの数をどうするか。それが「和と積の法則」
場合の数が2つ出てきた場合
●両立しない場合(または)→たし算する
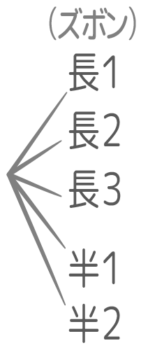
(例)長ズボン3種類と半ズボン2種類
→全部で3+2=5通りのファッション
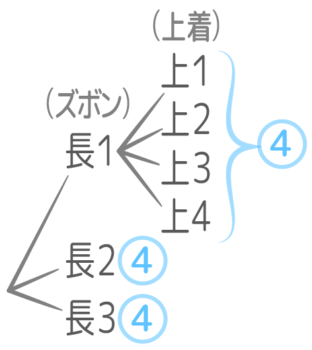
●両立する場合(そして)→かけ算する
(例)長ズボン3種類と上着4種類
→全部で3×4=12通りのファッション
テストで確認して下さい
1-3:和と積の法則
解説
長ズボン3通りと半ズボン2通りは同時に着れないので(和)ズボン全部で2+3=5通り
上着は4通り
ズボンと上着は同時に着れるので(積)、5×4=20通り
ヒント
サングラスには「かけない」という種類もあると考える
解説
ズボンは3+2=5通り、上着は4通り
サングラスは「かけない」「サングラス1」「サングラス2」の3通り
ズボン・上着・サングラスは同時に着れるので(積)、5x4x3=60通り
樹形図をイメージできるとベター
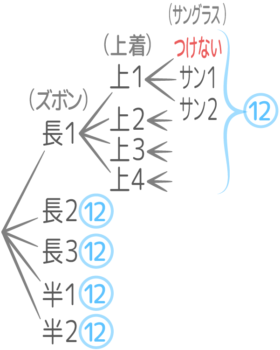
があることに注意する
もっと詳しい説明を見たい、いろんな問題を解きたい人は「場合の数の基本ルール」内の「和と積の法則」を見て下さい。
 爽茶
爽茶並べ方の拡張ルール
基本ルールを少し変えた並べ方
条件にそって並べる
条件を指定された場合、条件に沿うように計算を2回(以上)行って、和積の法則の「積」でかけ算して答えを出します
両端を指定
手順は「(両端を決める→)❶両端を並べかえる→❷残りを並べかえる→❸積を求める」(前後しても同じ)
2-1-1:両端指定
解説
❶両端の並べ替え
両端へのDEの座り方は「D…E」と「E…D」の2通り
❷残りの並べ替え
残り3席へのABCの座り方(3個の全部並べかえ)が3x2x1=6通り。
❸積
全部で2×6=12通り
樹形図はこんな感じ
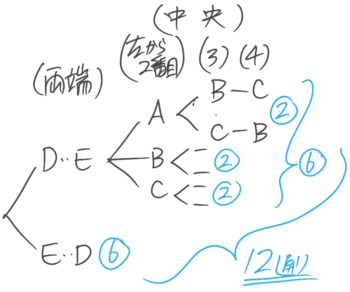
後半は省略して計算で出す
交互に並ぶ
手順は「①2種類の物(男女など)の配置を決める→❷1種類の並べ替え→❸もう1種類の並べ替え→❹積を求める」です。
配置が1通りしか無い場合①は必要なし
2-1-2:交互に並ぶ
解説
①配置
男女の並び方は「男女男女男」しかない
❷1種類目の並べ替え
男3人の並び方(3個の全部並べかえ)が3x2x1=6通り
❸もう1種類の並べ替え
女2人の並び方は2×1=2通り。
❹積
全部で6×2=12通り
ヒント
(1)との違いを考える
解説
①配置
男女の並び方は「男女男女男女」と「女男女男女男」の2通りある
❷1種類目の並べ替え
男3人の並び方(3個の全部並べかえ)が3x2x1=6通り
❸もう1種類の並べ替え
女3人の並び方は3x2x1=6通り。
❹積
全部で2x6x6=72通り
隣り合う
隣り合うよう指定された2人(ペア)を1人と考えるのがコツ
手順は「❶2人を1人と考えて全部並べかえ→❷2人の並び替え→❸積」です
2-1-3:誰かがとなり合う
解説
❶DEをまとめて[X]として「ABCX」4人の並べかえと考えると4x3x2x1=24通り。
❷さらに[X]の中で「DE」と「ED」の2通り
❸合計24×2=48通り
ヒント
ペアを2つ作ると…
解説
❶BDを[X]、CEを[Y]として「AXY」3人の並べかえと考えると3x2x1=6通り。
❷さらに[X]と[Y]の中でそれぞれ2通り
❸合計6x2x2=24通り
となり合わない
並び方には「となり合う並び方」と「となり合わない並び方」のどちらかしかないので、「並び方全部」から「隣り合う並び方」を引けば「となり合わない並び方」が出る
2-1-4:となり合わない
解説
●無条件で5人が並ぶと(5個の全部並べかえ)5x4x3x2x1=120通り
●女子がとなり合う並び方は(4x3x2x1)x2=48通り(上の「練習2-1-3」参照)
●となり合わないのは、120–48=72通り
詳しい解説が読みたい・もっと問題を解きたい人は「並べ方の拡張」を見て下さい
丸く並べる(円順列)
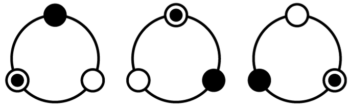
3つのものを丸く並べると
重複が3通りできる
普通の並べかえの答えを重複数で割らないといけない
●N個全部を丸く並べかえる
→N×(N-1)×(N-2)×…×1 ÷N 通り
(例1)5個全部を並べかえる
→5x4×3×2×1÷5=24 通り
●N個からA個えらんで丸く並べかえる
→N×(N-1)×…×(N-A+1)÷A 通り
(例1)7個から3個えらんで丸く並べかえる
w① ② ③
→7×6×5÷3=70 通り
問題をどうぞ
2-2:円順列
解説
6人座る=同じ並びが6通りできるので、6人全部並び替えを6で割ります。
6x5x4x3x2x1÷6=120通り
解説
3人座る=同じ並びが3通りできるので、一部並べかえを3で割ります。
6x5x4÷3=40通り
ヒント
円順列の割り算は1回だけでOK
解説
男子3人を円に並べるのは(3個の円順列)3x2x1÷3=2通り。
男子の間に女子3人を並べるのは3x2x1=6通り(これは円順列ではありません)
合計2×6=12通り
詳しい解説が読みたい・もっと問題を解きたい人は「並べ方の拡張」を見て下さい
丸くつなげる(数珠順列)
石のように裏表がないものを丸くつなげる(数珠のように)場合は、回転と裏返しで同じ並びが円順列の2倍できるので、円順列をさらに÷2する
~反対向きも同じに数える
●N個全部を数珠順列にする
→N×(N-1)×(N-2)×…×1 ÷N÷2 通り
(例1)5個全部を並べかえる
→5x4x3x2x1÷5÷2=12通り
●N個からA個えらんで丸く並べかえる
→N×(N-1)×…×(N-A+1)÷A÷2 通り
(例1)7個から3個えらんで丸く並べかえる
w① ② ③
→7×6×5÷3÷2=35通り
練習問題をどぞ
2-3:数珠順列
解説
7x6x5x4x3x2x1÷7÷2=360通り
解説
10x9x8x7x6÷5÷2=3024通り
詳しい解説が読みたい・もっと問題を解きたい人は「並べ方の拡張」を見て下さい
重複ある場合の数(色玉)
色のついた玉をあれこれする場合は、人間と違って同じものが何個かありますね
そのように重複する場合の選び方と並べ方を学びます
参考:全部違う色の場合
ちなみに、全部の玉の色が違う場合は「基本ルール」で学んだ方法と全く同じになります。(確認したい人は「開く」をクリック)
選び方
●N個から2個選ぶ→N×(N-1)2 × 1
(例)全て色の異なる5個の玉から2個選ぶ
→5 × 42 × 1=10通り
●N個から3個選ぶ→N×(N-1)×(N-2)3 × 2 × 1
(例)全て色の異なる6個の玉から3個選ぶ
→6 × 5 × 43 × 2 × 1=20通り
●N個から4個選ぶ→N×(N-1)×(N-2)×(N-3)4 × 3 × 2 × 1
(例)全て色の異なる10個の玉から4個選ぶ
→10× 9 × 8 × 7 4 × 3 × 2 × 1
=210通り
ならべ方
●N個全部を並べかえる
→N×(N-1)×(N-2)×…×1 通り
(例)異なる色の玉5個全部を並べかえる
→5×4×3×2×1=120 通り
●N個からA個えらんで並べかえる
→N×(N-1)×…×(N-A+1) 通り
(例1)異なる色の玉5個から2個えらんで並べかえ
w① ②
→5×4=60 通り
(例2)異なる色の玉7個から3個えらんで並べかえ
w① ② ③
→7×6×5=210 通り
重複のえらび方
同じ色が何回か使える場合に注意しながら、えらび方の「小さくなっていく数本の樹形図」を書いて調べる
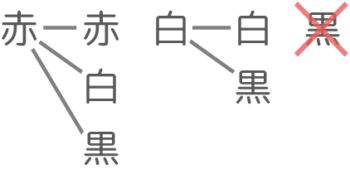
例1:赤玉3つ,白玉2つ,黒玉1つから2つの玉をえらぶ
例2:みかん2個,りんご1個,マンゴー1個,スイカ1個から2個えらぶ
例3:赤玉3つ,白玉2つ,黒玉1つから3つの玉をえらぶ
例4:みかん2個,りんご1個,マンゴー1個,スイカ1個から3個えらぶ
重複のならべ方
重複全部並べ
玉を置く穴が横一列に並んでいる板のようなものをイメージして…
((図))
個数が少ない色から置く位置を選んで、積の法則で合計を出す
例1:赤玉2個,白玉1個を並べかえる
穴が3つ横に並んだ板をイメージします。その3つの穴のうち白玉を置く穴を1つ選べば、残り2つは自動的に赤玉が入ると決まります
3つの穴から1つ選ぶのは=3個から1個選ぶので3通り(樹形図を書いても良い)
例2:赤玉7個,白玉3個を並べかえる
穴が7+3=10個並んだ板をイメージします。10個の穴のうち白玉を置く穴を3つ選べば、残りは自動的に赤玉に決まります
=10個から3個選ぶので、10 x 9 x 83 x 2 x 1=120通り
例3:赤玉2個,白玉3個,黒玉1個を並べかえる
全6穴のうち黒玉を置く穴1つを選ぶのに6通り、
残り5穴のうち赤が入る2つを選ぶのに5 x 42 x 1=10通り
残りの穴には自動で白が入る(1通り)。
合計(積)6x10x1=60通り
例4:赤玉2個,白玉3個,黒玉5個,青玉1個を並べかえる
全11穴のうち青玉が入る1つの穴を選ぶのに11通り
残り11-1=10穴のうち赤玉が入る2つの穴を選ぶのに10 x 92 x 1=45通り
残り10-2=8穴のうち白玉が入る3個を選ぶのに8 x 7 x 63 x 2 x 1=56通り
残り8-3=5穴は自動で黒玉に決まる(1通り)。
合計11x45x56x1=27720通り
重複一部並べ
一番面倒くさいパターン!
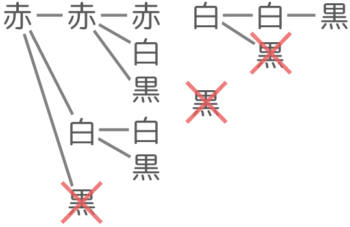
例1:赤玉3つ,白玉2つ,黒玉1つから3つの玉をえらんで並べかえる方法
まず、重複選び方の樹形図を書いて選び方が何通りあるか調べます(それぞれにA~Fまで名前をつけました)
A(赤赤赤),B(赤赤白),C(赤赤黒),D(赤白白),E(赤白黒),F(白白黒) と6通りの組み合わせがありました。
この組み合わせをそれぞれ並べ替える
Eは色の異なる3つの玉の並べ替え→3x2x1=6通り
BCDFは色が異なる1個の玉の位置が3通り→3通り
Aは並べ替えられません→1通り
これらの数値を合計して、6+(3×4)+1=19通りが答えです。
例2:みかん2個,りんご1個,マンゴー1個,スイカ1個から3個をえらんで並べかえる方法
同様に、まず選び方(組み合わせ)を調べると
A(みみり),B(みみマ),C(みみス),D(みりマ),E(みりス)
,F(みマス),G(りマス)の7通つの組み合わせがある
DEFGは単純な全部並べかえ→3x2x1=6通り
ABCは色が違う1個の玉の位置が3通り→3通り
合計して、(6×4)+(3×3)=33通り です
 爽茶
爽茶[作成中]図形の問題
図形のえらび方
点を選んで図形を作る問題
線を選んで三角形を作る問題
図形のならべ方
図形の数え方
 爽茶
爽茶数字カードの問題
数字が書かれたカードをあれこれする問題
カードのえらび方
和指定
「1から9まで書かれた数字カード9枚から和が7になるようなカードを2枚選べ」など
規則正しく数え上げていくと、(1,6)(2,5)(3,4)の3通り
「1から5まで書かれた数字カード9枚から和が3の倍数になるものを3枚選ぶ」だと(1,2,3)(1,3,5)(2,3,4)の3通り。これは「整数を作る問題」の「3の倍数を作る問題」で使います。
積指定
「1から6まで書かれた数字カードから積が6の倍数になるようなカードを2枚選べ」など
これも規則正しく数えていくと(1,6)(2,3)(2,6)(3,4)(3,6)(4,6)(5,6)の7通り。
「1から6まで書かれた数字カードから積が奇数になるようなカードを2枚選べ」のように偶数・奇数が条件の場合、かけ算の中に一つでも偶数が交じると答えも偶数になるのに注意します。
よって積が奇数になるには「1」「3」「5」だけでかけ算を作らないといけないので(1,3)(1,5)(3,5)の3通りと分かります。
「積が偶数になる」という条件の場合は、6枚のカードから2枚えらんで出来る組み合わせの合計(5+4+3+2+1=)15通りから奇数だけでできる3通りを引いて12通りと求めます。
カードのならべ方(整数を作る問題)
数字カードを選んで並べ替えることで整数を作ります。「1」と「3」を選んでも、順番によって「31」「13」二種類の整数が出来ます。
単純なパターン
「1から5の数字カードから3枚えらんで3ケタの整数を作る」などの問題は5個から3個えらんで並びかえるだけなので「選んで並べかえる公式」そのままで5×4×3=60 通りと解けますが、樹形図も書いてみます。
((樹形図))
整数を作る時は(百)(十)(一)と位を項目として必ず書きましょう。
番目の問題
「1から5の数字カードから3枚えらんで3ケタの整数を作るとき、小さい方から(大きい方から)3番目を求めよ」のように番目を指定された問題
個数の問題
「1から5の数字カードから3枚えらんで3ケタの整数を作るとき、300より大きい(小さい)数は何個あるか」のように個数を求める問題
「0」カードがある場合
「0から5の数字カードから3枚えらんで3ケタの整数を作る」のように「0」がある場合は要注意です。
百の位には「0」が来れないので5通り、十の位には百の位で使った数以外の5通り…と考えると5×5×4=100通りと分かりますが、慣れるまでは樹形図を書いて確かめましょう。
((樹形図))
ダブりのカードがある場合
同じ数のカードが2枚以上ある場合は単純な計算で求めるのは難しいです。サッと樹形図を書いて調べましょう。
「1,1,2,3,4」から3枚選んで3ケタの整数を作る場合はこうなります。
((樹形図))
これに「0」のカードが入ってくるとややこしくなるので落ち着いて調べましょう。
偶数・奇数を作る
偶数か奇数かは一の位で決まるので、まず一の位から考えます。
例えば「1から5の数字カード5枚から3枚えらんで3ケタの偶数を作る」場合は、まず一の位に来るのは2か4の2通り、百の位は一の位に使った数以外の4通り、十の位にくるのは残りの3通りなので2×4×3=24通りです。
この場合も「0」のカードが入ると面倒くさくなります。樹形図を書いて調べましょう。樹形図の項目は(百)(十)(一)ではなく(一)(百)(十)とします。
「0から5の数字カード6枚から3枚えらんで3ケタの偶数を作る」場合はこうなります。
((樹形図))
中学受験生は4年生のうちに書けるようにしておきましょう。
3の倍数を作る
3の倍数になる条件は「各位の和が3の倍数になる」なので、数の並べ替えをする前に「各位の和が3の倍数になる」組み合わせを選ばないといけません。
従って2ステップで解くことになります。
①和が3の倍数になる組み合わせを選ぶ
②選んだ組み合わせそれぞれで整数を作って合計
「1から5の数字カード5枚から3枚えらんで3ケタの3の倍数を作る」場合はこうなります。
①1から5の数字カード5枚のうち、和が3の倍数になる3つの数の組み合わせは(1,2,3)(1,3,5)(2,3,4)(3,4,5)の4つです。
②4つの組み合わせはそれぞれ並べ替えで3×2×1=6通りの整数ができるので、6通り×4つの組み合わせ=24通りです。
0が入ると多少面倒くさくなりますが、はじめの2つか3つの組み合わせを試すと後は数えなくても予想ができます。
「0から4の数字カード5枚から3枚えらんで3ケタの3の倍数を作る」場合はこうなります。
①和が3の倍数になる3つの数の組み合わせは(0,1,2)(0,2,4)(1,2,3)(2,3,4)の4つです。
②(1,2,3)(2,3,4)は3数の並べ替えで3×2×1=6通りの整数が作れますが、(0,1,2)(0,2,4)は0があるので2×2×1=4つしか整数を作れません。合計すると6+6+4+4=20通りです。
6の倍数を作る
6の倍数は2の倍数(一の位が偶数)と3の倍数(各位の和が3の倍数)の2つの条件を満たさないといけません。
問題を解く時は2ステップで解きます。
①和が3の倍数になる組み合わせを選ぶ
②選んだ組み合わせそれぞれで偶数を作って合計
「0から4の数字カード5枚から3枚えらんで3ケタの6の倍数を作る」場合はこうなります。
①和が3の倍数になる3つの数の組み合わせは(0,1,2)(0,2,4)(1,2,3)(2,3,4)の4つです。
②4つの組み合わせそれぞれで出来る偶数を数え上げます。(0,1,2)で出来る偶数は「102」「120」「210」の3つ、(0,2,4)で出来る偶数は「204」「240」「402」「420」の4つ、(1,2,3)で出来る偶数は「132」「312」の2つ、(2,3,4)で出来る偶数は「234」「324」「342」「432」の4つ、これらを合計すると3424=13通りです。
いや~面倒くさいですね(汗)
カードの並べ方(小数を作る問題)
小数点のカードが混じっている場合、小数も作れます。
関連記事「小数の応用問題」中の「小数点のあるカードの並べ替え」を見て下さい。
 爽茶
爽茶[作成中]「ゲーム」の問題
サイコロ・コイン・ジャンケンなどの場合の数
サイコロ
2つ以上のサイコロを振って出る目で条件に合う場合の数を数えます。
2つの場合
注意するのは、2つのサイコロの目を区別することです。
例えば「大小2つのサイコロを振って目の和が4になるのは何通りか」の場合、(1,3)(2,2)の2通りではなく、「大1,小3」「大2,小2」「大3,小1」の3通りになります。
6×6表の利用
サイコロ2つの問題では数え上げる以外にも「6×6の表(ひょう)」がオススメです。
((6×6表))
大小2つのサイコロを振って目の和が4になるのは何通りか上の問題の場合はこうなります。
((書き込んだ6×6表))
6表を書くことに慣れれば、数え上げるよりも早く確実に解けますよ。
3つの場合
サイコロの数が3つ以上の場合は、上で見た「数字カードで3の倍数の整数を作る」問題のように、❶まず組み合わせを求めて❷それぞれを並べ替える、という2ステップで解きます。
例えば「大中小3つのサイコロを振って目の和が6になるのは何通りか」の場合
❶和が6になる組み合わせは(1,1,4)(1,2,3)(2,2,2)です。
❷それぞれの組み合わせを大中小に並べ替えると、(1,1,4)からは「大1,中1,小4」「大1,中4,小1」「大4,中1,小1」の3通り、(1,2,3)からは3つの並び替えで6通り、(2,2,2)からは「大2,中2,小2」のみ1通りが出来るので、これを合計して3+6+1=10通りになります。
ゲームの問題
すごろくのように、サイコロの目でコマをすすめるような問題。
かなり複雑な問題もあります。
(作成中)
コイン
「少なくとも~」
よく出題される形式で注意するものは「少なくとも1枚は表」「少なくとも1枚は裏」というような条件指定です。これらの場合は「全部裏の場合」や「全部表の場合」が何通りか出して使います。
例えば「ABCDE5枚のコインを投げて少なくとも1枚は表が出ているのは何通りか」の場合は「全部裏の場合」を使います。
5枚のコインが全部裏になるのは1通りです。5枚のコインを投げた場合の数は全部で2×2×2×2×2=32通りなので、この32通りから「全部裏」の1通りを引いた31通りが答えになります。
「少なくとも2枚が表」の場合は全ての場合から「全部裏」の場合と「1枚だけ裏」の場合を引けば答えになります。
(作成中)
ジャンケン
2人以上でジャンケンをした勝ち負けの場合の数を求めます。
注意するのは3人のアイコの場合です。「全員が同じ手(全員グー,全員チョキ,全員パー)」の場合以外に「全員が違う手(グーとチョキとパー)」を数え忘れないことです。
(問題作成中)
「道」の問題
経路の問題
3地点以上を結ぶ様々な経路を考えて行き方や往復の仕方を計算する問題で、それぞれの経路の道の数をかけ合わせると答えになります。
基本
「A町→B町→C町と移動する。AB間には道が3つ、BC間には道が2つある場合、全部で何通りの行き方があるか」という問題の場合、3×2=6通りです。
往復の仕方の数
大抵の問題で「行きに使った道は通れない」という制限があります。そういう場合、帰りは道の数が-1されます。
「A町→B町→C町→B町→A町と往復する。AB間には道が3つ、BC間には道が2つある場合、全部で何通りの行き方があるか。ただし行きに通った道は帰りには使えない」という問題の場合、3(行きのAB)×2(行きのBC)×2(帰りのCB)×1(帰りのBA)=12通りです。
複雑な経路の問題
途中で二又に別れたり、別れた先で又別れたりという複雑な経路の場合は、道に名前をつけて樹形図を書くのが確実です。
(問題作成中)
道順(格子)の問題

スタート地点から碁盤の目のような町(条坊制の平城京・平安京をイメージ)を通ってゴールまで行く道順が何通りあるか数える問題
基本的な考え方
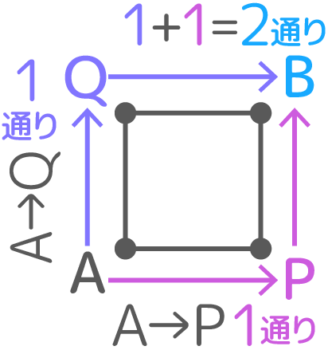
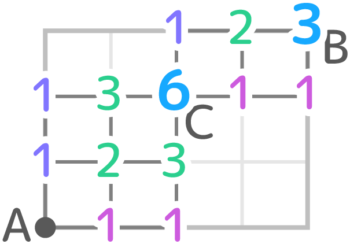
一番単純な正方形で左下のA地点から右上のB地点まで行く方法が何通りあるか考えます。
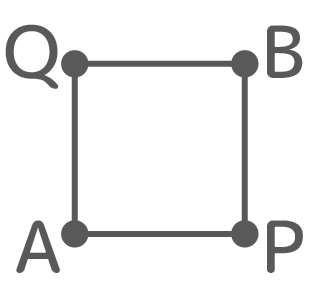
Bに行くにはA→P→BとA→Q→Bの2つの経路しかありません。
そしてA→P、P→B、A→Q、Q→B全部道は1つしかありません。ここで、上で見た経路の問題を思い出すと、A→P→Bは1×1=1通り、A→Q→Bも1×1=1通りしか無いことが分かります。
この2つを足してAからBへの行き方は1+1=2通りになります。
今の考え方をもっと単純に分かりやすく書くとこうなります。
まず左上の点Xと右下の点Yへの行き方はそれぞれ1通りしかないので「1」と書きます
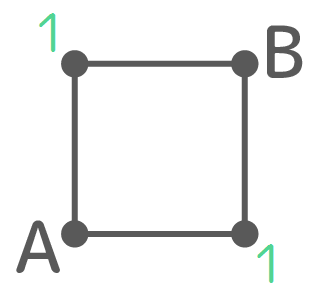
この2つの「1」を右と上にBに向けて合わせると1+1=2になります。これがAからBへの行き方の個数になります。

単純な形
今の考え方でもう少し大きな町を移動してみます。
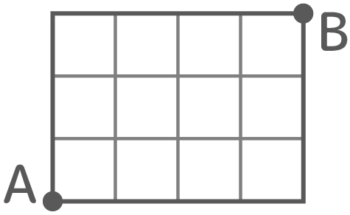
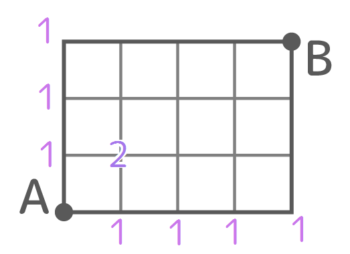
まずAから右と上に真っ直ぐ行った点は全て1通りなので「1」と書きます
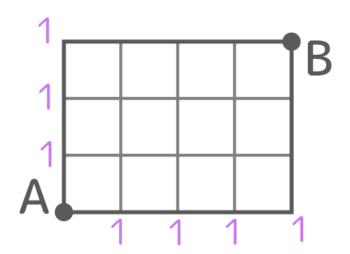
次に、さっきの正方形の右上にあたる点へ左と下から1を2つ合流させて1+1=2の「2」を記入します。
さらに、今書いた「2」を1と合流させて1+2=3の「3」を記入します
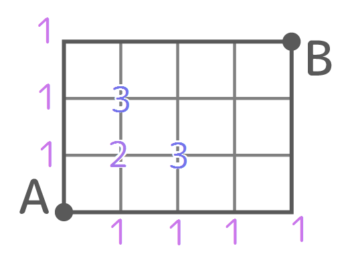
これを繰り返してBまで数字を記入します
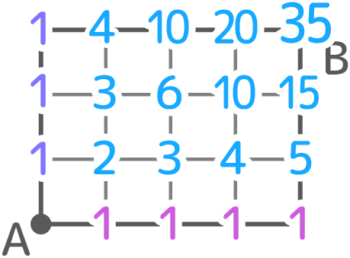
35通りと分かりました。
ゲーム感覚で面白く解けると思います。
不規則な形

一部が欠けたり…
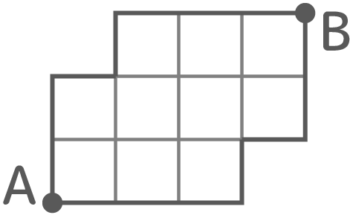
一部の区画が大きかったり…
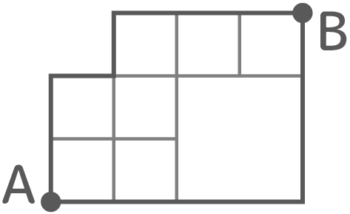
上のような不規則な形でも同じルールで出せます。
試しにやってみましょう(答えだけ示します)。
欠け形

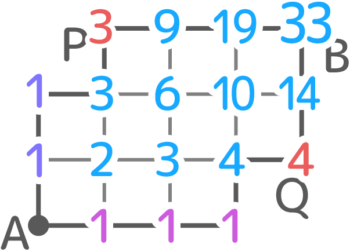
答えは33通り
不均等形

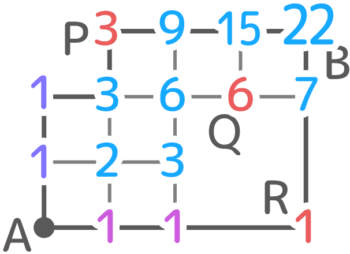
答えは22通り
中継地の指定
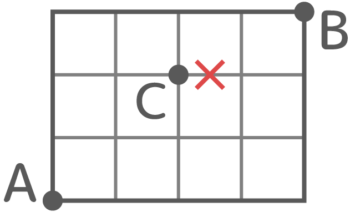
今まではAからBに行く全ての方法を出していましたが、「Cを通って行く方法を求めなさい」というような指定がある場合です。
ここでも経路の問題と同じ考えを使えば解けますね。A→Cの行き方とC→Bの行き方を求めて、かけ合わせれば良いのです。
A→C→B:6×3=18通り
A→Cが6通り、C→Bが3通りなので、A→C→Bは6×3=18通りです
通行禁止地点
例えば、「AからBまで図のXを通らずに行く方法は何通りか」という場合です。
上の方の「コイン」の問題(「少なくとも1枚が表」)で使った「全部の場合の数ー反対の条件の場合の数」の考え方を使います。
つまり、全部の場合からXを通る場合の数を引いて答えを出すのです。
Xを通る行き方はA→C→D→Bになります。
そしてA→Cは6通り(図1)、P→Cは1通り、D→Bは2通り(図2)なので、A→C→D→Bは6×1×2=12通りと分かります。
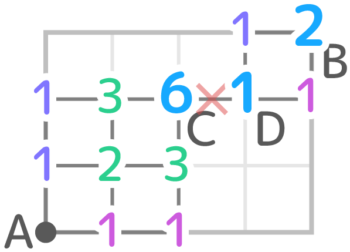
全部の場合の数は35通りなので、35ー12=23通りが答えになります。


三次元格子の道順

棒で作った立方体の骨組みの上を移動するような問題です。一見複雑そうですが、理屈は上で見た「条坊制」の問題と同じなので安心して下さい。
基本的な考え方
棒で作った立方体の骨組みのような立体を「三次元の格子」と呼びます。この三次元格子上の1点から1点へ行く道順を求めます
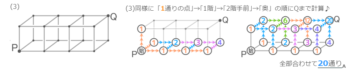
例えば
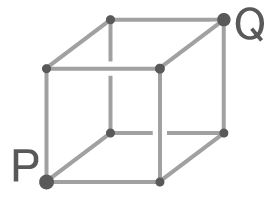
図のPからQまで行く道順は何通りか求める問題で、上で解いた条坊制と同じ作業を三次元で行います
Pから直接行けるのは3箇所(A,B,C)です
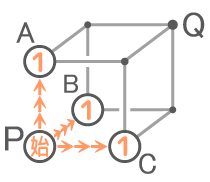
ABCを経由して行ける点をD,E,Fとすると、Dへの行き方は「P→A→D」と「P→B→D」の2通りで、E,Fへの行き方も同じく2通りです。
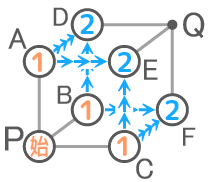
これは「条坊制」と同じく1+1=2という計算です。
さらに目的地QへはD,E,Fの3方向から行けるので、D,E,Fへの行き方を合計して2+2+2=6通りになります
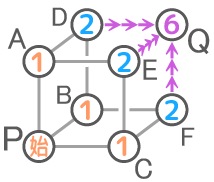
このQのような「3方向から行ける」点があるのが三次元の特徴になります。
一方向への延長
この考え方を使って、三次元の格子を奥(右方向)に増やしたカタチでのPからQへの行き方を考えると
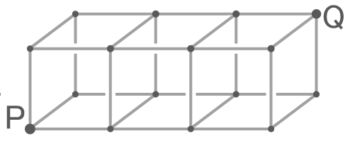
それぞれ、こうなります(答えのみしめします)。
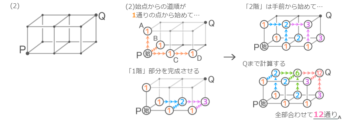
2,3方向への延長
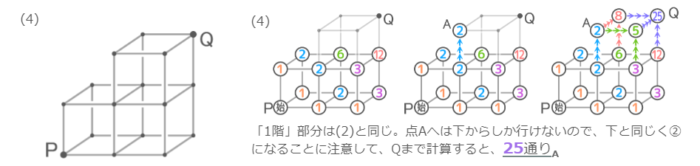
さらに「2階」を作るように縦方向にも延長してみます

「1階」部分は先程と同様です

「2階」部分は手前左側の点(A)から求めます。左,前,下3方向のうちいくつから行けるかを考えて合計します(答えのみしめします)
塗り分け問題
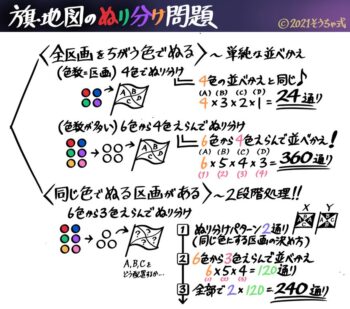
旗や地図を2色3色で塗り分ける場合の数を出す問題。今までの知識を総動員して解く問題です。
考えることが多くて頭がゴチャゴチャするので、考える手順を決めておくと安心して解けます。
塗り分けのルール
大きく2つの場合に分けて考えます
全区画をちがう色で塗り分ける場合
区画数と準備した色数が等しい
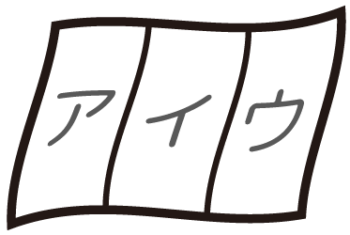
まず、旗の区画(色を塗る場所)と準備した色の数が全く同じ場合、例えば「図のような旗を青,白,赤の3色で塗り分ける方法は全部で何通りあるか」を考えましょう。
これは3つの色を並びかえる場合の数(「全部の並べかえ」)と同じですね。
●N個全部を並べかえる
→N×(N-1)×(N-2)×…×1 通り
(例1)5個全部を並べかえる
→5×4×3×2×1=120 通り
この問題ではN=3なので、3×2×1=6通りになります。

3 x 2 x 1 =6 通り
色の数が多い場合
色の数が区画の数より多い場合、例えば「図のような旗を青,白、赤,黒のうち3色で塗り分ける方法は全部で何通りあるか」を考えます。

4色のうち3色を選んで塗るので、これは4個から3個を選んで並びかえることになります。
●N個からA個えらんで並べかえる
→N×(N-1)×…×(N-A+1) 通り
(例1)5個から2個えらんで並べかえる
w① ②
→5×4=60 通り
(例1)7個から3個えらんで並べかえる
w① ② ③
→7×6×5=210 通り
この問題はN=4,A=3なので、4×3×2=24通りです。
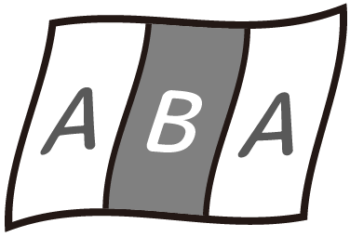
同じ色で塗る区画がある場合
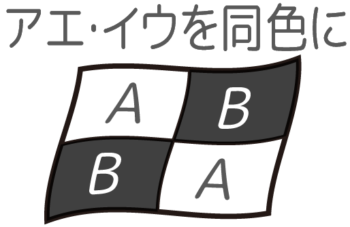
今までは区画を全部違う色で塗っていましたが、いくつかの区画を同じ色で塗らないといけない場合、例えば「図のような旗を赤・青・緑・紫のうち3色で塗り分ける方法は全部で何通りあるか」を考えます。
2区画は同じ色で塗ることになる。
この場合は2段階で処理をするのがポイントです。
まず、4つの区画を3色で塗るので同じ色で塗る区画をどこにするか(配色パターン)が何通りあるか考えます。
この旗の場合は「上下を同じ色で塗り左右は別の色にする」のと「左右を同じ色で塗り上下は別の色にする」の2通りあります。
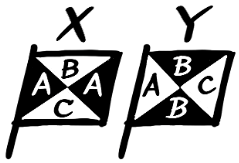
次に準備した4色から使う3色を決めて塗り分けます。これは4個から3個えらんで並べかえなので、4×3×2=24通りです。
配色パターンが2通りで塗り分けが24通りなので、合計で2×24=48通りになります。
これで塗り分け問題の解き方が分かってきましたね。色数が少ない場合2ステップになります。
- 同じ色で塗る区画がある場合は、塗り分けパターン(配色パターン)を決める
- 実際に塗り分ける
(「選んで並べかえ」か「全部並べかえ」) - ➀と②の数をかけ合わせる
では、このルールを使って旗や地図を塗り分けていきましょう
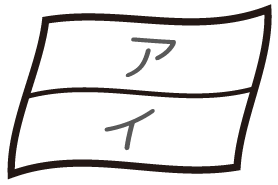
2区画の旗や地図

2区画の場合、同じ色で塗る区画はないので、単純な並べ方の計算一発で答えが出る
2色で塗り分け
例えば、赤と白の2色で並べ変える場合、2個の全部並べ替えなので、2×1=2通り
3色以上で塗り分け
3色の場合、3色から2色選んで並べ替えなので、3×2=6通り
4色の場合、4色から2色選んで並べ替えなので、4×3=通り
3区画の旗や地図
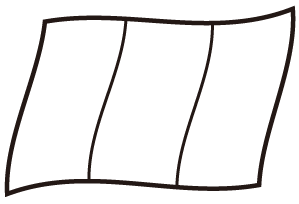
2色で塗る(同じ色で塗る区画がある)場合は、2段階の計算になる。
川の字形
上の例で出したいわゆる「三色旗」
与えられた3色で塗る
例えば、赤・青・白の3色で塗る場合は、基本ルールの「全部並べ替え」なので3x2x1=6通り

3 x 2 x 1 =6 通り
多色から3色選んで塗る
例えば、赤・青・白・黒の4色から3色選んで塗る場合は、基本ルールの「選んで並べ替え」で4x3x2=24通り
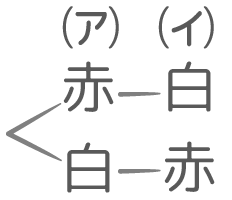
与えられた2色で塗る
例えば「赤」「白」二色で塗る場合
区画の数(3)より少ない色(2)で塗るので、同じ色で塗る区画があり、2段階の計算をしないといけない。
①まず同じ色で塗る区画のデザインが何通りあるか考えます。この場合は1通りしかありません
というパターンしかない
②赤と白2色の並べ替えは2×1=2通り
➂ ①と②を掛け合わせて1x2=2通りと分かります


多色から2色選んで塗る
この場合も2段階の計算をする
例えば「赤」「青」「白」3色から2色選んで塗る場合
①まず同じ色で塗る区画のデザインは1通り


②さらに3色から2色えらんで並べ替えは3×2=6通り
①と②をかけ合わせて1x6=6通り
4色から2色選んで塗る場合は、①同色にする区画は同じく1通り、②4色から2色を選んで並べ替えに4×3=12通り、➂掛け合わせて1x12=12通り
5色から2色選んで塗る場合は、1x(5×4)=20通り
Tの字形
((画像))
Tの字のような旗は3色でないと塗り分けられないので、同じ色で塗る区画を考えることはないのでラクチンです
多色から3色選んで塗る
例えば4色から3色選んで塗る場合は、基本ルールの「選んで並べ替え」で4x3x2=24通り
5色から3色選んで塗る場合は5x4x3=60通り
6色から3色選んで塗る場合は6x5x4=120通り
与えられた3色で塗る
基本ルールの「全部並べかえ」で3x2x1=6通り
変則形
2色で塗り分けられる(同じ色で塗る区画がある)場合は「川」と同じ計算に、3色必要な場合は「T」と同じ計算になる。
(例1)
例えば、このような旗は2色では塗り分けられないので「Tの字」と同じ計算になります。
(例2)
このような旗は2色で塗り分けられるので「川の字」と同じ計算になります。
ここから先も考え方は同じです。区画が増えると「同じ色で塗る区画のデザイン」が増えるのが面倒くさいです…
4区画の旗や地図
同色区画のパターン数が増えて複雑になってきます
十字形
十字で分けたような旗。
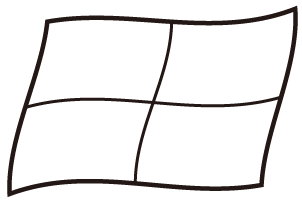

4色で塗る
4つ全部並べかえなので4x3x2x1=24通り
多色から4色選んで塗る
例えば5色から4色選んで塗るときは、5個から4個選んで並べかえと同じなので、5x4x3x2=120通り
3色で塗る
区画(4)より塗る色(3)が少ないので2段階で解く
①同色にする区画のパターンは2つ
同色区画のパターン

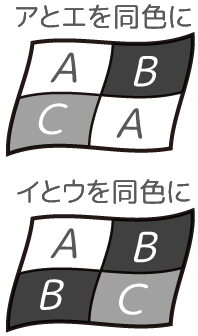
②3色を並べかえるので、3x2x1=6通り
➂ ①と②をかけ合わせて2×6=12通り
多色から3色選んで塗る
例えば5色から3色選んで塗り分ける場合
①同色区画のパターンは2通り②5色から3色えらぶのに5x4x3=60通り➂かけ合わせて2×60=120通り
2色で塗る
区画数より塗色数が少ないので2段階で解く
①同色区画のパターンは1通り
同色区画のパターン

②2色の並べかえは2×1=2通り
➂掛け合わせて1×2=2通り
多色から2色選んで塗る
例えば5色から2色選んで塗り分ける場合
①同色区画のパターンは1通り②5色から2色えらんで並べかえに5×4=20通り➂掛け合わせて1×20=20通り
川形
川+α形
変則形
5区画以上の旗や地図
同色パターンがさらに増えて面倒になります
確認テスト(2020.5.9作成中)
分ける問題
組分け問題
人を部屋(組)に分ける、物を山分けするなど
2つに分ける
不均等に分ける場合
単純な選び方の問題になる
例えば、5人の生徒ABCDEを2人部屋と3人部屋に分ける場合。5人から2人部屋に行く生徒2人を選べばよいので、5個から2個のえらび方になる。
4+3+2+1=10通り。または5×42×1=10通り
均等に分ける場合
この場合、単純な選び方だと同じ分け方を2回数えてしまっている。
例えば4人の生徒ABCDを2部屋に分ける場合、(A,B)を選ぶ場合と(C,D)を選ぶ場合は変わらないはずなのに2通りと数えているので正しい答えの2倍になっている。
そこで、(4個から2個選ぶ場合の数)÷2=(3+2+1)÷2=3通り が答えになる。
3つに分ける
完全に不均等に分ける場合
単純にえらび方を積にすればOK
例えば6人の生徒ABCDEFを3人部屋、2人部屋、1人部屋に分ける場合。一人部屋に泊まる生徒のえらび方が6通り、二人部屋に泊まる生徒の選び方が残り5人から2人を選ぶので 4+3+2+1=10通り、残りは自動で3人部屋に泊まるので1通り。この3つの場合の数をかけ合わせて(積の法則)、6×10×1=60通り
一部不均等に分ける場合
単純なえらび方の積だと2倍多く数えてしまう
例えば5人の生徒ABCDEを2人部屋、2人部屋、1人部屋に分ける場合。一人部屋に泊まる生徒のえらび方が5通り、二人部屋に泊まる生徒の選び方が4人から2人を選ぶので 3+2+1=6通り、残りは自動でもう1つの二人部屋に泊まるので1通り…だが、4人から2人を選ぶ時に同じ選び方を2回数えている(例えばABCDの(A,B)と(C,D))ので、選び方の積を÷2しないと正しい答えにならないので、5×6×1÷2=15通り
均等に選ぶ場合
単純なえらび方の積だと6倍も多く数えてしまう
例えば6人の生徒ABCDEFを2人部屋、2人部屋、2人部屋に分ける場合。えらび方の積は、6人から2人選ぶ(15通り)×4人から2人えらぶ(6通り)×2人から2人えらぶ(1通り)になるが、これだと同じ分け方例えば(A,B)(C,D)(E,F)を6通り数えてしまっている。
(A,B)(C,D)(E,F)、(A,B)(E,F)(C,D)、(C,D)(A,B)(E,F)、(C,D)(E,F)(A,B)、(E,F)(A,B)(C,D)、(E,F)(C,D)(A,B)
よって、えらび方の積を÷6しないと正しい答えにならないので、15×6×1÷6=15通り になる。
整数の分解
和に分解
連続する整数の和に分解
例えば、6=1+2+3のように、ある整数を連続する数の和に分解する問題
→ある数Aが奇数の約数(1とその数自体を除く)を
N個持つ場合、「連続する数の和」に分解する方法もN通りある
(例1)15を「連続する数の和」に分解する方法
→奇数の約数(1と15自体を除く)は3,5の2個
→「連続数の和」に分解する方法も2通りある
(例2)8を「連続する数の和」に分解する方法
→奇数の約数が無いので0通り
実際の分解の様子など詳しくは関連記事「整数を連続する数の和に分解する」を見て下さい
金額の問題(作成中)
お金が好きな人は多いでしょう♪
決まった金額を作る問題
例えばこんな問題です。
作れる金額を求める問題
選んで使う場合
全て使う場合
例えばこんな問題です。
試合の数
多くのチームで試合をして順位を決めるには、大きく分けて2つの形式がある。
リーグ戦(総当り戦)…サッカーのワールドカップの予選
トーナメント戦(勝ち抜き戦)…ワールドカップの決勝大会
リーグ戦
Nチームでのリーグ戦(総当り戦)の試合数=N個から2個のえらび方
5チームのリーグ戦なら、5個から2個のえらび方
→4+3+2+1=10 または 5C2=5×42×1=10試合
トーナメント戦
Nチームでのトーナメント戦(勝ち抜き)の試合数=N-1
1試合するごとに1チーム消えて、これを残り1チームまで行うから
16チームでのトーナメント戦なら、16-1=15試合
●A人(チーム)のリーグ戦
(A人から2人を選ぶ場合の数)
→(A-1)+(A-2)+…+1 または AC2=A×(A-1)2×1
(例)5チームのリーグ戦
→4+3+2+1=10 または 5C2=5×42×1=10試合
●A人のトーナメント戦
(1試合で1人が消える)
→ (A-1)試合
(例)16人のトーナメント戦→16-1=15試合
問題を解いてみましょう
X-1:試合数を求める
予選はリーグ戦で、ABC地区では4チームから2チームが、D地区では6チームから3チームが選ばれる。
本戦は各地区の代表がトーナメントで戦う。優勝が決まるまで全部で何試合あるか(引き分けや再試合は無かったとする)
ヒント
あせらず予選の試合数と決勝の試合数を出しましょう♪
解説
ABC地区の予選リーグは、4チームから2チームの選び方で3+2+1=6試合ずつ。D地区では6チームから2チームの選び方で5+4+3+2+1=15試合。予選の合計試合数は6×3+15=33試合。
決勝トーナメントは2+2+2+3=9チームでのトーナメントなので、9-1=8試合
合計して33+8=41試合
確からしさ(確率)
確からしさとは
「全部の場合」に対する「条件を満たす場合」の割合を「確からしさ」と言う
例えば、サイコロを1個振った時に偶数の目が出る確からしさ(確率)
サイコロを1個振るとき場合の数は全部で「1」「2」「3」「4」「5」「6」の6通りあります。
そのうち、問題文の条件「偶数」を満たす場合の数は「2」「4」「6」の3通りです。
したがって、サイコロを1個降った時に偶数の目が出る確からしさは36約分して12になります。(百分率にすると12×100=50%です。)
このように「確からしさ」とは「全部の場合の数」を分母に、「条件を満たす場合の数」を分子にした分数になります。
~全部の場合に対する条件を満たす場合の割合
=条件を満たす場合の数全部の場合の数
(例)サイコロを1個ふった時に偶数の目が出る確からしさ
→全部の場合は6通り、条件を満たすのは3通り
→確からしさは36=12
問題を解いてみましょう
X-1:試合数を求める
解説
コインを3枚投げて出る目の全部の場合の数は(表、表)(表、裏)(裏、表)(裏、裏)の4通り
「確からしさ」では「えらび方」と違って(表、裏)と(裏、表)を別々に数えます
一方、条件を満たすのは(裏、裏)の1通り
よって確からしさは14
ヒント
(ここにヒントが入ります)
解説
少なくとも1枚表が出るのは(表、表)(表、裏)(裏、表)の3通り
よって確からしさは34
別解
「少なくとも」と言われたら、全部の場合からダメな場合を引いても同じです。
この場合、全部の場合4通りからダメな場合(裏、裏)の1通りを引いても 4-1=3通り と同じになりました♪
このやり方だと、全部の場合の数が多いときがラクに答えが出せるのでオススメです
次はコインを増やしましょう
X-1:確からしさ(コイン)
解説
全部の場合は、(数え上げても良いですが)計算で出すとコインAが表と裏の2通りxコインBも2通りxCも2通り=8通りになる
条件を満たすのは(表、表、裏)(表、裏、表)(裏、表、表)の3通り
よって確からしさは38になる
ヒント
「少なくとも」と言われたら?
解説
「条件を満たす場合」を「全部の場合」から「ダメな場合」を引いて求める。
「ダメな場合」は全部裏の(裏、裏、裏)の1通りなので、条件を満たすのは8-1=7通り
よって確からしさは78になる
ヒント
問題文の前半の条件で「全部の場合」が減ります
解説
「表が出ているとき」なので全部裏の1通りを除いた7通りが「全部の場合」になる
さらに「裏も出ている」という条件は「少なくとも1枚は裏」と同じなので、全部の場合7通りからダメな場合(全部表)1通りを引いた6通りが「条件を満たす場合」になる
「全部の場合」が7,「条件を満たす場合」が6なので、確からしさは67になる
その他の問題
オススメ教材
 爽茶
爽茶分かりやすい!と評判のスタディサプリにも「場合の数」の授業動画がありますよ。今なら14日間無料。興味がある人は「先取りや予習・復習に! スタディサプリ そうちゃ式のオススメ利用法」へ
●場合の数だけを解きたい場合は「場合の数①」・
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題」シリーズ(日能研)
●小6受験生には「算数ベストチェック」(日能研)
お知らせ
2022年春
解答解説にミスがございました。大変失礼致しました!コチラです。
誤:「15×6×1÷2=45通り」→正:「15×6×1÷6=15通り」
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ