「面積図って何?」難しそう…」という小学生と保護者の方へ。
面積図自体は難しくありませんよ!うまく使うと「頭」で考えても分からない問題を「目」で解けるようになる便利な道具です。
東大卒講師歴20年の図解講師「そうちゃ」が分かりやすくまとめました。
面積図の基本
面積図の意味
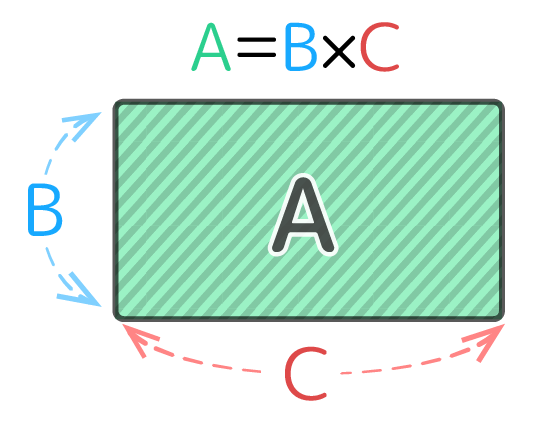
3つの数量A,B,Cが「A=B×C」の関係にある時は、長方形の面積の公式「面積=たて×よこ」と同じ関係なので、「面積をA、たてをB、よこをC」にした図ができます。
受験算数ではこの図を「面積図」と呼んでいます。
詳しくは「単純な面積図」を見て下さい。
L字形の面積図(つるかめ算)
2種類のモノを扱う場合、それぞれの種類に関する単純な面積図をくっつけた「L字形の面積図」を使います。有名なつるかめ算の面積図はこれです。
例えば「1個100円のアンパンと1個120円のクリームパンを合わせて10個買ったら、1080円になった」の場合、面積図は下のようになります。
((図))
この図から「●」または「○」の大きさを求めます
くわしくは「L字型の面積図」を見て下さい。つるかめ算の問題は「つるかめ算を面積図で解く」を見て下さい。
重なる面積図
→面積が同じ形が重なっているとき、
重なっていない部分(はみ出し部分)
の面積も等しくなる
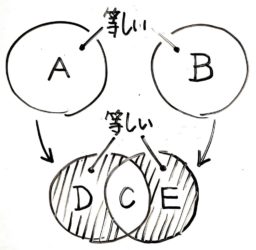
合同な図形の重なり
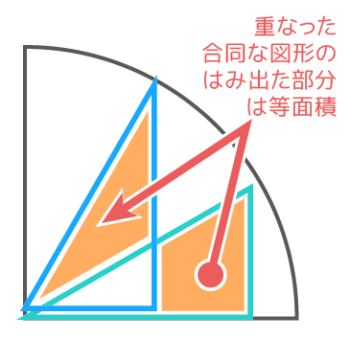
全く同じ図形AとBを重ね、重なっている部分をC、はみ出した部分をDEとすると、Dの面積=Eの面積となりますね。
なんとなく直感で分かると思いますが、A=B=10cm2、C=3cm2とすると、D=10-3=7cm2=E で等しくなります。
この考え方は、扇形の中にある三角形の面積が小さなおうぎ形と等しいとして計算する問題で使います(入試に頻出)
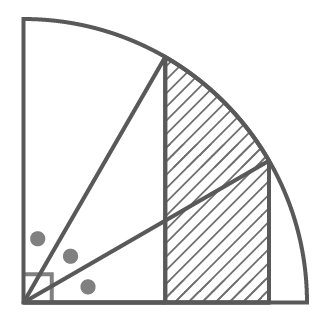
斜線部の面積を
を求める
等しいので
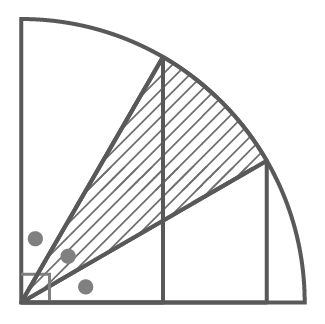
おうぎ形の
面積になる
右の扇形の面積と等しくなる
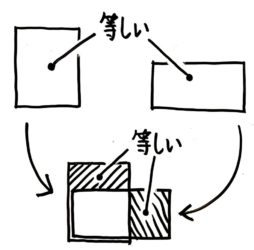
面積が同じ長方形の重なり
今度は形が違うけれど面積は同じである二つの長方形を左下角をピッタリ重ねます。この場合も上と同じ理屈ではみ出した部分は等しくなります。
面積が同じ長方形とL字形の重なり
重ならない部分
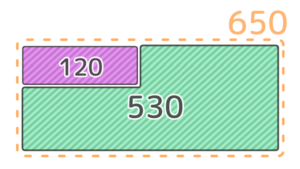
片方がL字型の場合は「長方形からハミ出た部分(A)」と「長方形とのすき間(B)」の面積が等しくなります。
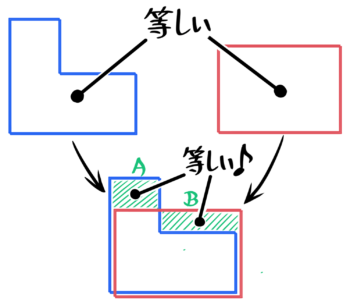
AとBの縦・横の合わせて4つの長さのうち1つが分からなくても、面積が等しくなる性質を利用して求めることができます。
例えばAの縦が4で横が6、Bの縦が3で横が分からない(?)場合、4×6=3x? なので、?=4×6÷3=8と分かりますね
この形は「平均算」などで使います。
比の学習後
比を学習した後は「面積が等しい2つの長方形の縦の比と横の比は逆になる」性質を使って、長さが2つしか分からない場合にも問題を解くことはできます。
例えばL全体の横の長さが39、Aの縦が9、Bの縦が4 の場合、AとBの縦の比は9:4なので横の比は4:9になります。AB合わせた全体の横が39なので、Aの横は39x44+9=12、Bの横は39-12=27と分かります
同じ面積を加える
重ならない部分に同じ面積を加えても面積は等しいままです
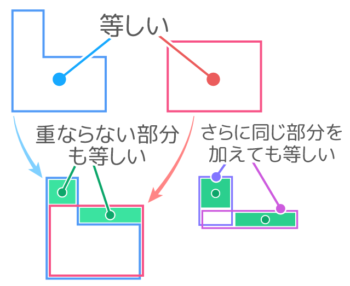
さらに同じものを加えても等しいまま
この考え方を利用すると、比を使わなくても解ける問題が増えます
面積が同じL形の重なり
横幅(合計個数)が同じL形を重ねた場合にも、重ならない部分の面積は等しくなる
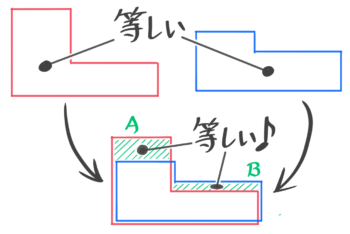
重なる面積の「差」
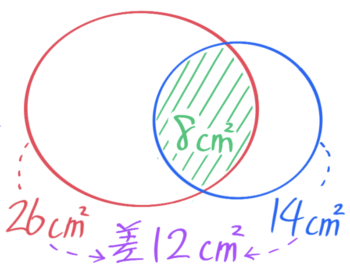
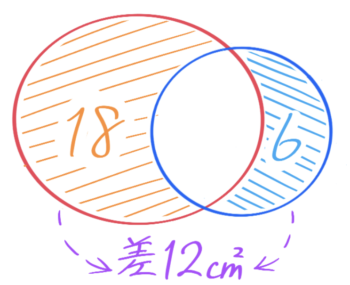
2つの図形が重なる場合、はみ出た2つの部分の差は元の図形の差と等しくなります。
例えば、面積26cm2の図形と14cm2の図形が8cm2重なっている場合、面積の差は26-14=12cm2です。
そして、はみ出た2つの部分の面積は26-8=18cm2と14-8=6cm2なのでこちらの差も18-6=12cm2で、等しくなりました♪
けっこう使うことが多いルールなので、図と日本語で記憶して下さい。
面積図を使った解法の例
平均算
平均算の中でも難しい問題は面積図を使って解きます。
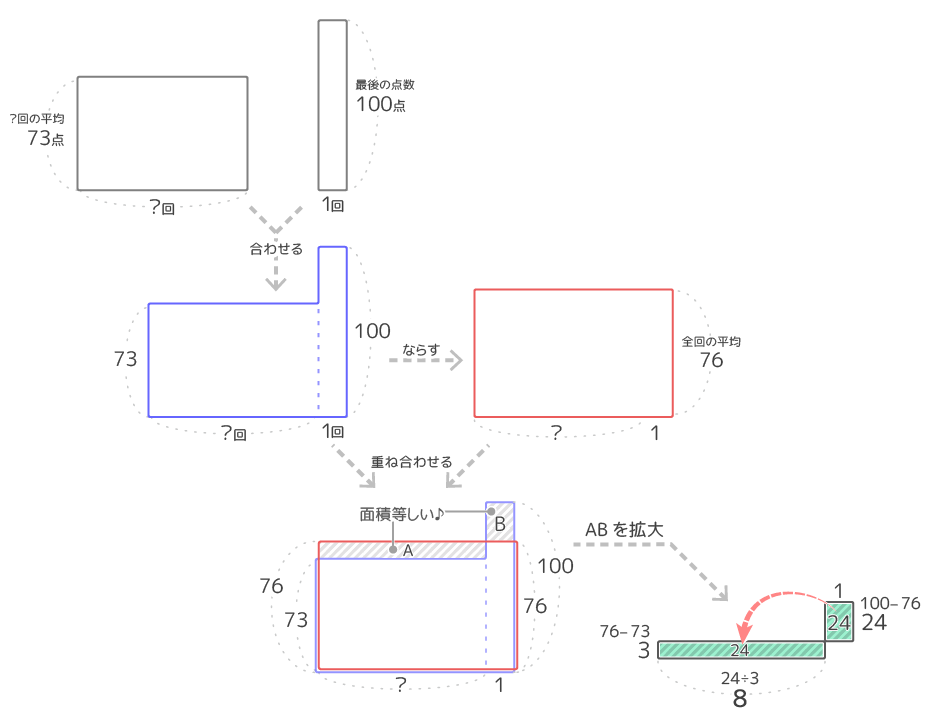
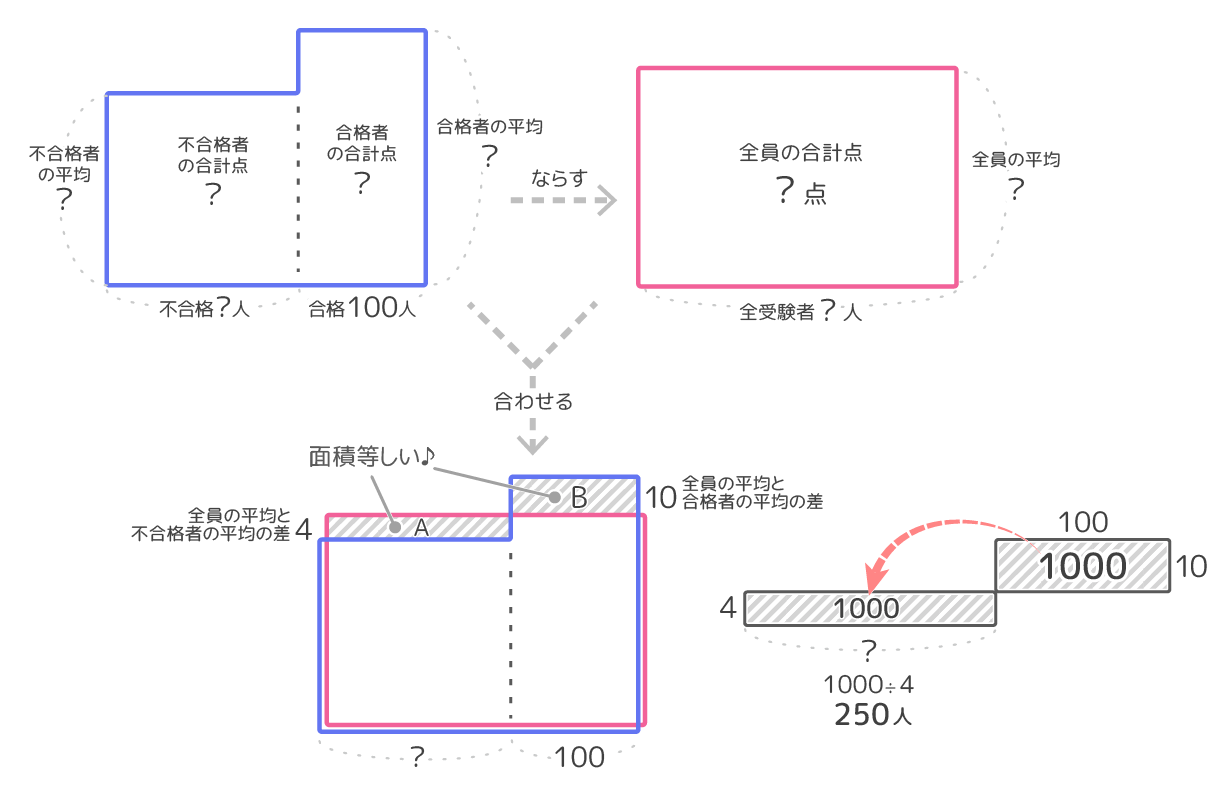
詳しくは参考記事「平均算」を見て下さい。
つるかめ算
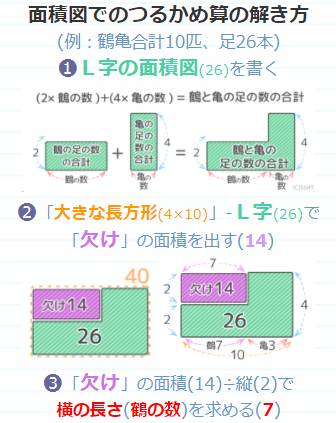
過不足算
複数の売買計算
仕事算
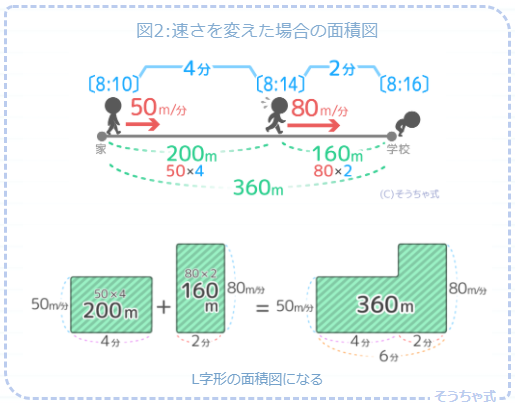
速さの変化
次のステップへ
最後まで読んでいただきありがとうございました。この記事があなたの役に立てたなら嬉しいです。