「周期算って何?」という小学校低学年から「周期算を復習したい」という中学受験生の方、おまかせ下さい。
東大卒講師歴20年の図解講師「そうちゃ」が分かりやすくまとめました。
確認問題で定着を図れるので、記事を読めば周期算はもう大丈夫ですよ!
周期算の基本
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
はじめに「周期算」の簡単な紹介・説明をします周期算は、同じパターンが繰り返し出てくる物や数の並びについての問題です。
例えば、白と黒の石が図のように並んでいる場合
○○●●○○●●○○●…
よく見ると石が4個ずつの並び(周期=パターン)を繰り返しているのが分かる。
○○●●/○○●●/○○●…
また、数字が図のように並んでいる場合も
3,1,4,3,1,4,3,1,4,…
数字が3個ずつの並びを繰り返している。
3,1,4,/3,1,4,/3,1,4,…
このパターン(周期)を利用するのが周期算です。並びを見たら周期に区切れないか考えて区切ってみましょう。
確認問題をどうぞ
●○○○●●○○○●●○…
→( ●○○○●/●○○○●/●○…で5個ずつの周期 )
3212321232…
→( 3212/3212/32…なので4個ずつの周期 )
ご石の並び
上で上げた碁石の並びで9番目の石が何色か考えます。
➀②➂④
➄⑥⑦⑧
⑨⑩⑪⑫
実際に数えて色を見ると…白です。
これを計算で出すにはどうすればよいか考えましょう
位置を探る
まず9番目の石が周期との関係でどのような位置にあるのかを求めます。
9番目までに「○●●○」の周期がいくつ出てくるか割り算で計算すると9÷4=2…1なので、「○●●○」の周期が2個出てきます。余りの「1」は、2周期の後に1個あるという意味で、これが9番目になります。
➀②➂④/
○●●○/
➀②➂④/
➀②➂④/
○●●○/
➄⑥⑦⑧/
➀②➂④/
○●●○/
⑨⑩⑪⑫/
第3グループの1番目と分かる
つまり9番目の石は第3グループの1番目です。そして、どのグループでも1番目は白なので9番も白と分かります。
このように周期算で何番目かを指定されたら、まず割り算で位置を探ります。
では100番目の石は?
100÷4=25…0なので、100番目の石は25周期の後の0番目、つまり25周期の最後の石です。
➀②➂④/
○●●○/
➀②➂④/
/➀②➂④/
/○●●○/
/⑨⑨⑩100/
第25グループの最後
どのグループでも最後の石は白なので、100番目の石は白と分かります。(つまり、余りが0の場合は周期の最後になる。)
公式としてまとめるとこうなります。
●1周期A個の時、最初からN番目の数の位置
N÷A=B…C の時
第B周期の後のC個目=第(B+1)周期のC番目
(C=0の時は、第B周期の最後)
(例)1周期5個の、最初から34番目の数の位置?
→34÷5=6…4
→ 第6周期の後の4個目=第7周期の4番目
確認テストをどうぞ
1周期が3個の時、最初から43番目の位置は?
→( 52÷3=17…1より18(17+1)周期の1番目 )
1周期が5個の時、最初から70番目の位置は?
→( 70÷5=14…0より14周期の最後(5番目) )
三種類の番号
このように、周期算の計算では三種類の番号が出てきます(色をつけていました)。

これがラクに解くコツです。
A通し番号~初めから連続して数える番号
B周期番号~周期(グループ)の番号
C周期内番号~周期の中で数える番号
この三種類の番号を意識すると、石の位置が分かりやすくなります。
色別の石の数合計
位置を探ることができれば色んな問題を解けます。
例えば、50番目までの石すべてを取ると黒石は何個あるでしょうか?
まず50番目の石の位置を探ります。
50÷4=12…2 なので12周期の後の2個目つまり第13周期の2番目です。
➀②➂④/
○●●○/
➀②➂④/
/➀②➂④/
/○●●○/
/㊽㊽㊽㊽/
➀②
○●
㊾㊿
第13グループの2番目
ここで、一つの周期(グループ)の中に黒い石は2個ずつあるので、第12周期までの黒い石は全部で2×12=24個あるのが分かります。
さらに第13周期は2番目までしか石が無く黒い石は1個しかありません。
➀②➂④/
○●●○/
黒石2個 /
/➀②➂④/
/○●●○/
/ 黒石2個 /
➀②
○●
黒石1個
これを合計して、黒い石は24+1=25あると分かりました!
確認テスト
65番目までの石すべてを取ると黒石は何個あるか?
→( 65番目の位置を求めると、65÷4=16…1なので、17周期の1番目の白石 )
→( 各周期の●を計算すると、1周期に●は2個あるので、16周期までに黒石は2×16個、17周期は1番目の白石で終わるので黒石は出てこない )
→(合計すると、2×16+0=32個 )
100番目までの石すべてを取ると白石は何個あるか?
→( 100÷4=25…0なので、100番目の石は25周期の最後(4番目))
→( 1周期に白石は2個あるので全部で2×25=50個 )
色別の順番から通番を求める
上の問題とは逆向きの問題も解けます。
例えば「黒い石だけを集めた時に16番目になる黒い石は、はじめから何番目か」
黒い石は1周期に2個づつあるので、黒い石だけを考えれば1周期2個の周期算と考えれば良いですね。
16番目の黒い石の位置を探ると、16÷2=8…0なので8周期の「最後の黒い石」と分かります。
➀②➂④/
○●●○/
➀②➂④/
/➀②➂④/
/○●●○/
/㊽㊽㊽㉘/
➀②➂
○●●
㉙㉚㉛
8周期の「最後の黒い石」と分かる。
そして8周期の「最後の黒い石」は…白い石も混ぜて数えた時は8周期の3番目(7周期の後の3個目)なので、はじめから数えると(4×7)+3=31番目になります。
確認テスト
色の差の問題
今度は周期を変えてみます。
((図))
この周期の 番目までの石を足すと、黒石と白石の数の差は何個になるでしょうか?
1周期に含まれる黒石は3個、白石は2個なので、1周期ごとに黒石が1個多くなっていきます。
そして、 番目の石は ÷ = … で、第 グループの 番目にあります。
((図))
グループの合計では1× = 個だけ黒石が多くなっていて、最後の グループでは黒石が 多いので、結局黒石が 個多いと分かりました。
((図))
周期算の公式
ここまでで何度も出てきた計算(公式)を確認します。
➀はじめから何番目→何周期の何番目
➁何周期の何番目→はじめから何番目
この2つです。
1つの周期にAコの数が入っている時
◆最初からN番目の数の位置は?
→N÷A=B…C の時
→第B周期の後のC個目=第(B+1)周期のC番目
→C=0の時は第B周期の最後
(例1)1つの周期に5個の数がある時、最初から34番目の数の位置?
→34÷5=6…4 → 第6周期の後の4個目=第7周期の4番目
(例2)1つの周期に6個の数がある時、最初から30番目の数の位置?
→30÷6=5…0 → 第5周期の最後(余り0は最後)
◆第P周期のQ番目の数は最初から何番目?
→(P-1)×A+Q 番目
(例3)1つの周期に5個の数がある時、第8周期の2番目は最初から何番目?
→(8-1)×5+2=37番目
(例4)1つの周期に6個の数がある時、第4周期の後ろから2番目の数は最初から何番目?
→後ろから2番目は後ろに1個あるので前から6-1=5番目
→(4-1)×6+5=23番目
ご石の並びの利用
自動点滅ランプ
自動で数秒間点灯した後に数秒間消えて、また点灯して…を繰り替えす電球の状態を計算する問題
スイッチを入れると自動で「2秒ついて3秒消える」を繰り返す電球を考える。
1秒間ごとに点灯を○、消灯を●と考えれば、
○○●●●○○●●●○○●●●…と「○○●●●」の5つを周期とするご石の問題と同じように考えることができる
注意1:1つ目の○は0秒から1秒まで(時間)の状態を表し、点灯する瞬間の時刻ではありません。点灯する時刻は0秒後になります。
注意2:点灯が1秒しかなく、点灯する瞬間の時刻を聞かれる問題は点灯する時刻を使った倍数の問題として解くのが簡単です
例題
スイッチを入れると自動で「2秒ついて3秒消える」を繰り返す電球がある。
(1)スイッチを入れてから60秒間で電球がついている時間は何秒間か
(2)電球がついている時間が111秒間になるのはスイッチを入れてから何秒後か
(1)60÷5=12…0 より60秒間は12周期ちょうど
1周期で点灯している時間は2秒間なので、2×12=24秒間点灯していると分かる
(2)111÷2=55…1より55周期と1秒間で111秒点灯したことになる。
55周期は5×55=275秒間、残りの1秒間は周期はじめの1秒間なので、276秒間つまりスイッチを入れてから276秒後に111秒点灯したことになる。
記号・文字の並び
ここまでは白石黒石の2種類しか並んでいませんでしたが、記号や文字を使うと3種類以上になって少し面倒くさいですが、やり方は変わりません。
例として、5文字のアルファベット「CYCLE」を並べた周期算を考えてみましょう(cycleは英語で周期の意味)。
CYCLE/CYCLE/CYCLE…
1周期にCが2個入っている
Q1.初めから82個目の文字は何か?
→82÷5=16…2より、初めから84個目の文字は第16周期の後の2個目(第17周期の2番目)。
→各周期の2個目はいつも「Y」なので、84個目も「Y」
Q2.82個目の文字までの中に「C」は何個あるか?
→82個目の文字は第16周期の後の2個目(第17周期の2番目)の「Y」
→1周期に「C」は2個あり、第16周期までに2×16=32個あるが、最後の第17周期は2番目で終わっているので「C」は1個だけ。
→合計で「C」は32+1=33個ある
Q3.23個目の「C」は初めから数えると何番目か?
→23÷2=11…1なので、23個目の「C」は第11周期の後1つ目の「C」(12周期の1つ目の「C」)
→周期の1つ目の「C」は他の文字を混ぜても周期の1番目の文字
→第11周期の後1つ目の「C」は初めから数えると5×11+1=56番目になる。
➀②➂④➄/
C Y C L E/
➀②➂④➄/
/➀②➂④➄/
/C Y C L E/
/㊽㊽㊽55/
➀
C
56
12周期の1番目の「C」
確認テスト
2021.1.22作成中
数字の並び
数字の並びも考え方は同じですが、数字同士を計算できるので複雑な問題も出題されます。
N番目の数を求める
碁石の「N番目の石の色を求める」のと同じやり方です。
例えば「269269…」という数字の並びの17番目の数を求める場合、1周期の個数が3個なので、17÷3=5…2 で位置を探って第6周期の2番目と分かります。
周期の2番目なので「6」になります。
(例)「2,6,9,2,6,9…」の17番目を求める
→1周期に3個の数があるので17÷3=5…2で、5周期の後の2個目(第6周期の2番目)と分かる。
→周期の2番目なので「6」
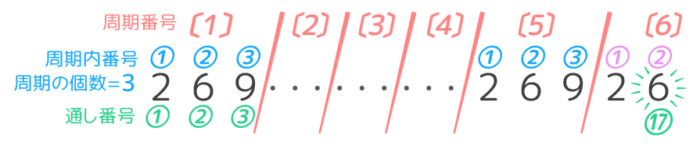
→Nを1周期の個数(A)で割った答えがB,余りCの時、N番目の数はB個の周期が出た後のC個目=第(B+1)周期のC番目。
N番目までの合計を求める
碁石や記号には無かった問題です。
例えば「269269…」という数字の並びを17番目まで合計したらいくつになるか?
まず17番目の数字の位置を探って、17÷3=5…2 で第6周期の2番目。
この問題では1周期の合計は17です。そして第1周期から第5周期の合計が17×5=85になります。
第6周期は「⑯2」と「⑰6」の2個しかないので合計は8です。
全部を合計すると85+8=93になります
(例)「269269…」を17番目まで合計すると?
→1周期「2,6,9」の合計が17
→17番目の数の位置は 17÷3=5…2 で5周期の後の2番目
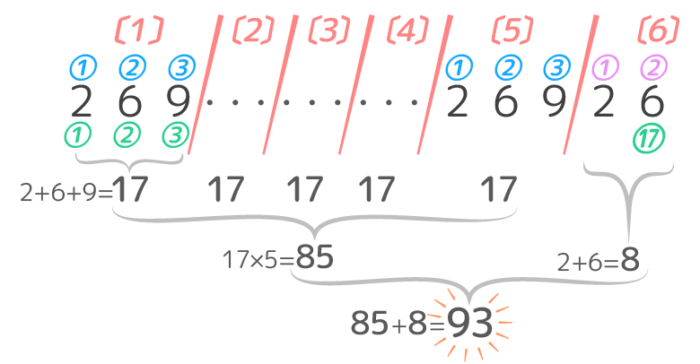 →5周期までの合計は17×5=85
→5周期までの合計は17×5=85
→6周期の合計は⑯2+⑰6=8
→合計は85+8=93
(問題を解く手順)
- 1周期の合計を出しておく(S)
- N番目の数の位置(第B周期の後C個目)を探る。
- 第B周期までの合計をS×Bで求める
- 最後の周期の合計を足し算で求める
- 全部を合計する
合計からN番を求める
上とは反対の問題で、例えば「269269…」という数字の並びをはじめから合計して になるのは何番目か?
数字の並びの応用
循環小数の並び
1÷3を計算すると(または13を小数に直すと)、割り切れずに「0.333…」と同じ数が並びます。
また1÷7を計算すると(または17を小数に直すと)「0.142857142857…」と「142857」という6個の数字が繰り返し並びます。
このような数を「循環小数」といいます。この数の並びを使った周期算の確認問題をどうぞ。
1÷7を計算をした時、小数第32位の数字は何ですか?
→( 1÷7=0.142857142857…でこれは1周期に6個の数を含む数の並びになっている。)
→( 32番目の数は、32÷6=5…2なので5周期の後の2個目、つまり6周期の2番目の数「4」と分かる。)
累乗の一の位の並び
3、3×3、3×3×3、3×3×3、3×3×3×3、3×3×3×3×3 という数の並びを計算して並べ直すと、3,9,27,81,243,729 になります。
さらに一の位だけを並べ直すと、3,9,7,1,3,9…と「3971」という4個の数字が繰り返し並びます。この数の並びも周期算として出題されます。
ちなみに、3×3×3のように同じ数を何回かかけた数を「累乗」と言います。この問題は「3の累乗の一の位の周期算」です。
8を2014回かけた数の一の位は?
→( 8,4,2,6,8,4,2,6…という4個周期になるので、
2014番目は 2014÷8=504…2より、505周期の後の2番目と分かるから「4」)
参考までに1ケタの整数の累乗の1の位を整理するとこうなります。
1の累乗→1,1,1,1,1…ずっと1(当然)
2の累乗→2,4,8,6/2,4,8,6…
3の累乗→3,9,7,1,/3,9,7,1…
4の累乗→4,6,/4,6…
5の累乗→5,/5,/5…ずっと5
6の累乗→6,/6,/6…ずっと6
7の累乗→7,9,3,1,/7,9,3,1…
8の累乗→8,4,2,6,/8,4,2,6…
9の累乗→9,1,/9,1…
累乗の元になる数
ある数Aを 回掛け合わせると一の位が になる。Aを求めよ。
番号順の当番
日付の並び(カレンダー)
日付は一週間7日を周期とした並びになっています。これを利用して周期算の問題が作れます。
ここで気を付けてほしいのは、日にちの数え方には二種類あると言うこと
◆「日後」=(間の数)=「日目」-1
◇「日目」=(木の数)=「日後」+1
●2つを互いに変えられるようにする
今日から10日目=今日の9日後
今日の7日(一週間)後=今日から8日目
植木算の前後の「数え方」の単元でカレンダーの問題を学んだ時は○「日後」を使いました。(日付の計算は「日後」を使ったほうが簡単なので。詳しくは「日歴算の解き方」を見てください。)
ところが単なる日付計算でなく「曜日ごとに異なった作業があるような問題」では周期算で「日目」を使うほうが簡単です。
算数が得意な人は、この機会に「日目」のやり方に統一しても良いでしょう。
例題1
Aさんは130ページの問題集を買ってきて、9/1(月)から月・木には3ページ、土曜日には5ページ進めていきます。
(1)9/10には何ページ進んでいますか?
→1週間に3+3+5=11ページ進みます。
→9/10は9/1から数えて、10-1=9日後=10日目です。
→10日目の周期上の位置は10÷7=1…3 より1週間の後の3日目つまり水曜日
→1週間で11ページ進み、さらに水曜日までに月曜の3ページ進むので、合計11+3=14ページ進んでいる(先が長い!…)
(2)50ページが終わるのは何月何日の何曜日ですか?
→50÷11=4…6なので、4週で44ページ終わらせた次の週に6ページ終わらせれば良い。
→6ページ終わらせるには月・木の3+3でちょうど終わるので、50ページが終わるのは4週の後の木曜日。
→4週の後の木曜日は、7×4+月花水木の4=32日目=31日後
→9/1の31日後の日付を求める。9月の残りが29日なので31-29=2より、10/2と分かり、これは木曜日であった。
(3)問題集が終わるのは何月何日の何曜日ですか?
→130÷11=11…9より、11週の翌週の土曜日に終わるのが分かる。
→11週の翌週の土曜日は7×11+6=83日目=82日後
→9/1の82日後は、82=29+31+22 より11/22(土)と分かる
例題2
Aさんの倉庫は工場で出来た製品を保管しています。月曜から金曜は1日8個の製品が倉庫に入ってきます。水曜に16個、金曜日に20個の製品を販売店に出荷します。現在のの日付は4月6日の月曜日で、倉庫の中は空っぽです。
Q1.来週の月曜日の朝には倉庫に製品が何個ありますか?
→倉庫には、1週間で8×5=40個の製品が入ってきて、16+20=36個の製品が出ていくので、40-36=4個の製品がたまっていきます。
→来週の月曜の「朝」はまだ製品が来ていないので、今週増えた4個の製品が倉庫にあります。
Q2.4/30に倉庫には製品が何個ありますか?
→今日が4/1なので4/30は30日目。
→30日目の周期上の位置を探ると、30÷7=4…2より5週目の2日目(つまり火曜日)と分かる。
→4個づつ4週荷物が増えるので5周目のはじめには荷物が16個たまっている。
→5周目の月曜と火曜は8個づつ製品が入ってくる(出荷はしない)ので16個増える。
→合計して16+16=32個が倉庫の中にあると分かる
Q3.このペースで行くと、倉庫の中の製品が50個になるのは何月何日の何曜日ですか?
並列する周期
2つの異なる周期が同時にスタートする場合
さらに大きな周期を考える
例えば、2つの異なる周期で点滅する電球
スイッチを入れてから2秒点灯して1秒消え、また2秒点灯して1秒消える電球Aと、スイッチを入れてから1秒点灯して3秒消え、また1秒点灯して3秒消える電球Aがある。同時にスイッチを入れる
1秒間の点灯状態を○・消灯状態を●とすると、Aは「○○●」3つを1周期とし、Bは「○●●●」4つを1周期とすると考えられる。
(注意:ABともに1秒しか点灯しない場合は、点灯する瞬間の時刻を使って単なる公倍数の問題として解くのが手軽です)
ABの周期を並べて書き出してみると、
A:○○●○○●○○●○○●○○●…
B:○●●●○●●●○●●●○●●●…
ABを混ぜて書き、Aだけ点灯を「●」Bだけ点灯を「●」AB同時に点灯を「●」とすると、
A&B:●●●●●●●●●●●●/●●●●●…
3と4の公倍数12を1周期とするさらに大きな周期を発見できた。
この考え方を使って問題を解きましょう
Q1同時に点灯している時間(秒)
Q2 Aだけが点灯している時間
Q3 Bだけが点灯している時間
Q4 ABどちらかが点灯している時間
Q5 ABどちらかも消えている時間
 爽茶
爽茶●周期算だけを練習したい場合は「周期算」(サイパー算数)
●周期算だけでなく算数全体の復習をしたい場合、小4受験生には「算数の基本問題4年」(日能研)
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
