「暦・カレンダーを使った問題が苦手！」な中学受験生の方へ
確かに月の日数が色々変わったりして面倒なんですが、主なルールは「大の月・小の月」と「うるう年」の2つだけ。また曜日の計算は7で割って余りを出すだけ。
これらのルールとやり方を自分のペースで良いので確実に理解練習すれば、必ずできるようになりますよ！
この記事では、暦のルールから日暦算の解き方まで東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
この記事を読んで例題がとけるようになれば日歴算が得意になっているかも?!
「日目」と「日後」の違い
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
2023年度の生徒さん募集中です
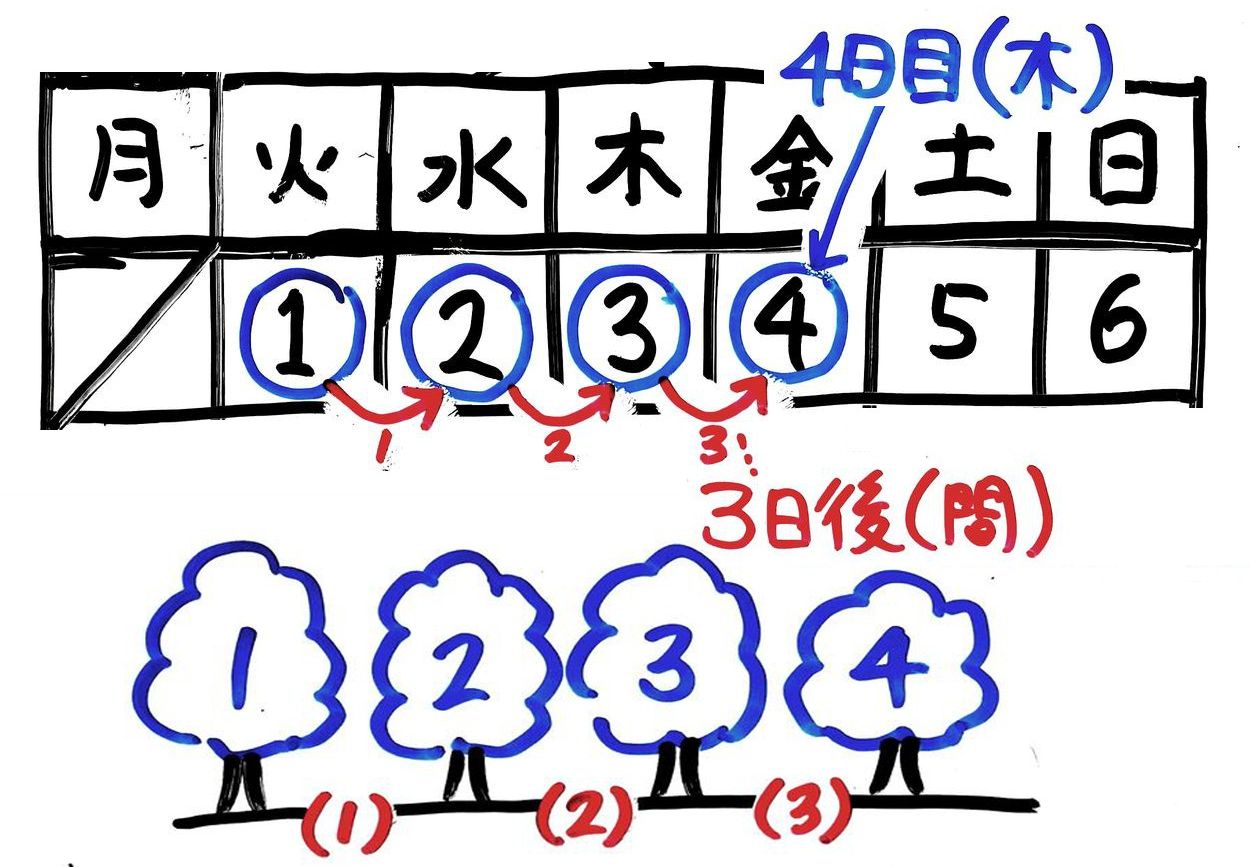
この2つの数え方の違いは「当日」を入れるかどうか！
「日目」は当日(今日)を入れて数えるのに対して、「日後」は当日を入れません。
例えば、今日が火曜日として今週の木曜日は「4日目」で「3日後」になります
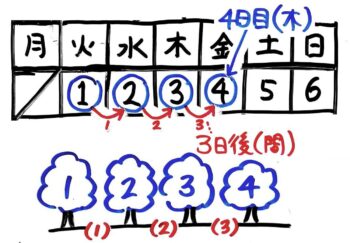
そのため「日後」は「日目」より1小さくなります。
●「日目」は当日を数えるが「日後」は数えない
●「日後」は「日目」より1小さくなる。
(例)4日目=3日後
念の為、確認テストをどうぞ
1-1:「日目」と「日後」
解説
日後は日目より1小さくなるので、4日目=4-1=3日後
解説
「日目」は「日後」より1大きくなるので、10日後=10+1=11日目
ヒント
一週間は何日？
解説
一週間は7日なので、一週間後=7日後
「日目」は「日後」より1大きくなるので、7日後=7+1=8日目
「日目」と「日後」は植木算(両端に木を植える場合)の「木の数」「間の数」と同じ関係です。(知らない・分からない・忘れた人は関連記事「植木算まとめ」を見て下さい)
◆「日目」(木の数)
＝「日後」+1
◆「日後」(間の数)
=「日目」-1
(相互に変換する)
今日から10日目＝今日の9日後
今日の7日(一週間)後＝今日から8日目
番号を数えるときの「番目」「番差」も似ていますね
直線状に両端にも植えるタイプの植木算と似ている
「番目(木の数)」＝「番差(間の数)」+1
「番差(間の数)」＝「番目(木の数)」－1
●計算は「番目」を「番差」に直して(-1)行う。
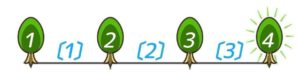
(例)左から1番目の木から数えて4番目の木の番号
→4番目＝3番差なので、1番目+3番差=4番目
ちなみに私の授業で最初に学習する際(小3～4年)には、「日後」で計算を行うよう指導しています。
「7日後が同じ曜日」というのが日常生活での用法に近く、直感的に理解しやすいからです。
ただし、曜日ごとの作業を考えるような問題では「日目」の考え方を使います。(関連記事「周期算」内「カレンダー」を見て下さい)
暦の特別ルール
爽茶もともと自然の世界には半端な数があって当たり前ですが、それを人間が無理やりきっちりした数(整数)の暦(カレンダー)にしたので、どうしても余りや不足が出てきます。
そこで特別なルールで調整する必要があるのです。
大の月・小の月・2月
暦上の「月」を2種類に分けます。
31日まである月を「大の月」、31日まで無い月を「小の月」と言います。
小の月は2月,4月,6月,9月,11月で、「西向く侍(にしむくさむらい)」とおぼえます。
サムライ=武「士」で、「士」がじゅういちと読めるので、「に・し・む・く・じゅういち」で「2,4,6,9,11」になるというわけです。
さらに、2月は28日までしかありません。
●大の月→31日まである月
(1,3,5,7,8,10,12)
●小の月→31日までない月
○4,6,9,11月は30日まで
○2月は28日まで(*うるう年は29日まで)
★小の月の覚え方
「西向く侍(に・し・む・く・さむらい)」
＝2・4・6・9・11(十一=「士」武士)
うるう年
一日多い年
普通の年の2月は「28日」までですが、4年に一回「うるう年」では2月が1日増えて「29日」までになります。
この結果、普通の1年が365日なのに対して「うるう年」は1年が366日になります。
うるう年の判定
ちょっとだけ面倒です…
原則
「うるう年」は、4の倍数の年です。
4の倍数かどうかは下2ケタ(十の位と一の位を数字として読む)が4で割り切れるかどうかで識別します。
(倍数の識別を知らない・忘れた人は参考記事「倍数の識別法」を見て下さい)
例えば、「2004」や「712(大宝律令)」は下2ケタが4の倍数なので「うるう年」ですが、「2011」や「239(卑弥呼の遣魏使)」は下2ケタが4の倍数でないので「うるう年」ではありません。
例外
ただ、下2ケタが「00」の場合は、400の倍数でないと「うるう年」にはなりません。つまり、その上の2ケタが4で割り切れないといけません
例えば、「400」や「1600(関ヶ原の戦い)」は下2ケタが「00」ですが、その上の数二桁が4の倍数なので「うるう年」です。
一方、「1500」や「300」は下2ケタが「00」で、その上の二桁が4の倍数でないので「うるう年」ではありません。
＝4年に一度、2月が29日までになる
→1年が365日から366日になる
●判定法(原則)
4の倍数の年=下2ケタが4の倍数の年
○例外
100の倍数の年=下2ケタが00の年→うるう年で無い
(例)100,200,1900,
○再例外
400の倍数の年=下2ケタより上が4の倍数
→うるう年になる
(例)400,1600,2000
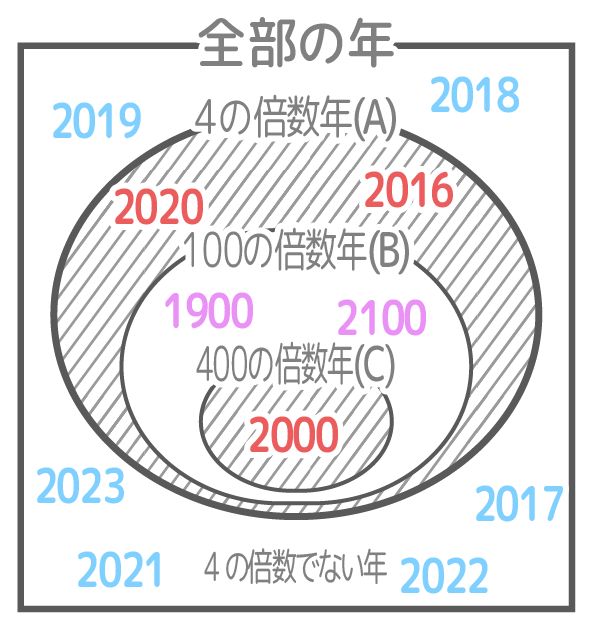
分かりづらいので、図にしてみました。
練習問題をどうぞ
2-1:うるう年の判別
解説
下2ケタ「20」が4の倍数なので「うるう年」です!
解説
下2ケタ「18」が4の倍数でないので「うるう年」ではありません
解説
下2ケタが「00」なので、その上の数が4の倍数か考える
上のケタ「19」が4の倍数でないので「うるう年」ではありません
解説
下2ケタが「00」なので、その上の数が4の倍数か考える
上のケタ「20」が4の倍数なので「うるう年」です！
解説
今年は2022年で、下2ケタ「22」が4の倍数でないので、うるう年ではありません
これで、ある年が「うるう年」かどうかは判断できるようになりました♪
うるう年の回数計算
爽茶ルールが複雑なので迷わないように公式にしておきましょう
もう一度、うるう年の判別をベン図に表すとこうなります。
基本的な「うるう年」は4の倍数(図のAの内部)
そのうち、100の倍数は「うるう年」ではない(図のBの内部)
しかし、そのうち400の倍数は「うるう年」になる(Cの内部)
結局、うるう年になるのはA-B+Cの部分です(斜線の部分)
あとは、年数を1から続く数と考えて倍数の個数の問題と考えれば計算できるでしょう
●1からNまでの間にあるAの倍数の個数
→N÷A個(余りは無視)
→100÷3=33…1→33 個
●NからMまでの間にあるAの倍数の個数
→(M÷A)-((N-1)÷A) 個(余りは無視)
*N-1になる事に注意！
→(100÷3)-((50-1)÷3)=33-16=17個
習っていない・忘れた・分からない人は参考記事「公倍約数まとめ」内の「倍数の個数」を見て下さい。
では、練習問題で試してみましょう♪
2-3:期間内のうるう年の回数
解説
A(1から500まで数のうち、4の倍数の個数):500÷4=125回
B(1から500まで数のうち、100の倍数の個数):500÷100=5回(100,200,300,400,500の5回)
C(1から500まで数のうち、400の倍数の個数):500÷400=1回(400のみ)
うるう年の回数=A+B-C=125-5+1=121回です！
ヒント
1868から2022までの間にある4の倍数の個数は(2022÷4)-{(1868-1)÷4}=(2022÷4)-(1867÷4)です。1868-1にするのに注意！
解説
A(4の倍数の個数):(2022÷4)-(1867÷4)=505-466=39個
B(100の倍数の個数):(2022÷100)-(1867÷100)=20-18=2個(1900年と2000年)
C(400の倍数の個数):(2022÷400)-(1867÷400)=5-4=1(2000年)
うるう年の回数=A+B-C=39-2+1=38回です！
分かりましたか？
4の倍数の年
→2月が29日まである(A)
ただし100の倍数の年
→うるう年ではない(B)
さらに400の倍数の年
→うるう年になる(C)
●うるう年の回数
→A-B+Cで決まる
(例)1868年から2022年までに、うるう年は何回あったか
A:(2022÷4)-(1867÷4)=505-466=39回
B:(2022÷100)-(1867÷100)=20-18=2回
C:(2022÷400)-(1867÷400)=5-4=1回
→A-B+C=39-2+1=38回
ここまでで暦(カレンダー)のルールが理解できました。
いよいよ日暦算(カレンダー計算)の問題を解いていきます
2つの日付を用いる問題
日暦算には大きく分けると2つのタイプがあります
●2つの日付を使った問題
(例)2001年1月1日から数えると2001年12月25日は何日後ですか？
(例)2001年1月1日が月曜日だとすると、2001年の12月25日は何曜日ですか？
●1つの日付(起算日)に日数を加える問題
(例)2001年1月1日の100日後は何月何日何曜日ですか
この章では、はじめのタイプを説明します
○/○は何日後か
基本的計算手順
日前の計算
日目で答える
1年以上離れた日付
○/○は何曜日か
曜日の計算方法
日付→日数・曜日
○回目の□曜日
○/○は何日後か
爽茶はじめは、日付Aを基準に日付Bが何日後(前)かを求める問題です
基本的な計算手順
最初に誘導に乗って例題を解いてみましょう
3-1:日後計算
解説
❶5月の残り日数は？
5月は大の月なので、残りは 31-27=4日
❷5月と8月の間の月の日数は？
5月と8月の間は6月と7月です
6月は小の月(+30)、7月は大の月(+31)なので、合計すると 30+31=61日
❸8月の日数は？
8/15なので15日
❶～❸を合計すると？
4+61+15=80日後 が答え
このように、日後の計算は3ステップで行います。
❶始まり日付の月の残り日数
❷間の月の日数
❸終わり日付 を求めて…
❶❷❸を合計する
(例)5/27から数えて8/15は何日後か？
❶31-27=4
❷30(6月)+31(7月)=61
❸15
→4+61+15=80日後
分かりましたか？誘導なしの練習問題をどうぞ
3-1:日後計算
解説
→❶9月は小の月なので、9月の残り30-1=29日
❷間は10月(+31),11月(+30)で合計61日
❸12/25の25日を足して、29+61+25=115日後 が答え
ヒント
翌年がどんな年か考えて下さいね
解説
❶11月は小の月なので、11月の残りは30-1=29日
❷12月は大の月(+31)、翌2020年はうるう年で、1月は+31、2月は+29
❸3月の11日を足して、29+31+31+29=120日後
分かりましたね？
日「前」の計算
AはBの何日前かを計算する場合、何日後かの計算の逆になります。
3-2:日前計算
解説
❶8/15の15日に
❷間の6月は小の月(+30)、7月は大の月(+31)なので、30+31=61日
❸さらに5月の残りが31-27=4日
合計して 15+61+4=80日前 が答え
気づいた人もいるでしょうが、これは例題2-1「5/27から数えて8/15は何日後か？」と答えは同じで、途中計算も❶～❸が逆になっているだけです。
ですので「○日前」の計算は(日付を入れ替えて)「○日後」の計算をすれば良いのですね
「AはBの何日前か」=「BはAの何日後か」を計算すれば良い
(例)5/27は8/15の何日前か=8/15は5/27の何日後か
→(31-27)+31+15=90日前(後)
念の為、練習してみましょうか
3-3:日前計算
解説
11月末は11/30なので、11/30が6/17の何日後かを求めて、答えるときに「後」ではなく「前」にすれば良い。
❶6月の残りが 30-17=13日
❷間の月は 7(+31),8(+31),9(+30),10月(+31) の小計123日
❸11/30の30日
以上を合計して 13+123+30=163日「前」 が答え
分かりましたね？
日目で答える
何日目ですか？と聞かれたら、「日目(木)=日後(間)+1」の関係を思い出して、+1して答えれば良い
試しに、上の方で解いた例題
3-1:日後計算
これの最後の部分を変えた問題を解いて下さい
3-4:日目計算
解説
日後計算は4+30+31+15=80日後
80日後=80+1=81日目
分かりましたね？
1年以上離れた日付
爽茶1年以上離れた日付の日数を聞かれる問題です
3-4:離れた日付の日数計算
これを今までの「月ごとの日数を合計する」方法で解くのは気が遠くなりますね…
そこで、(うるう年の2月が含まれない場合)1年=365日なので「1年後の同じ日付は365日後」ことを利用します。
通常の年だけの場合
例題で解法を理解して下さい
3-4a:離れた日付の日数計算
解説
2004年5月27日から3年後の2007年8月15日までに「うるう年」の2月29日はあるか？
ありません(2004年2月29日の次は2008年2月29日)
❶ちょうど3年後の2007年5月27日は何日後か？
1年=365日なので、ちょうど3年後の2007年5月27日は365×3=1095日後
❷2007年5月27日から数えて2007年8月15日は何日後か？
例題2-1と同じ計算で4(5月の残り)+61(6月,7月)+15(8月)=80日後
❶と❷を合計して答えを出すと？
1095+80=1175日ですね
うるう年を含む場合
うるう年の2月29日を含んでいる場合は、日数が1日増えます。
計算途中で365を366に変えるのが分かりやすいですが、慣れてきたら「うるう年」の回数をメモしておき、計算の最後で加えても良いでしょう。
例題をどうぞ
3-4b:離れた日付の日数計算
解説
●2004年5月27日から10年後の2014年8月15日までの間に「うるう年」の2/29は何日あるか？
2004/2/29の後は、2008と2012の2回ある。計算の最後に2を足すことを忘れずに！
❶2004年5月27日からちょうど10年後の2014年5月27日は何日後か
1年=365日なので、365×10=3650日後
❷2014年5月27日から2014年8月15日は何日後か
例題2-1と同じ計算で4(5月の残り)+61(6月,7月)+15(8月)=80日後
●と❶と❷を合計して答えを出すと？
3650+80+2=3732日ですね(2を足すのを忘れずに！)
では誘導なしの練習問題を解いてみましょう
(2022.8.1作成中)
○/○は何曜日か
爽茶曜日の計算方法
「7日後が同じ曜日」というのはよく使います。同じように14日後、21日後…というように7の倍数日後は同じ曜日です。
7の倍数＝7で割り切れる数なので、「日後」の数を7で割りきれる場合は同じ曜日、1余る場合は次の曜日、2余る場合は次の次の曜日…と分かります。
例えば今日が月曜日だとして、100日目(=99日後)の曜日は「99÷7=14余り1なので火曜日」と計算します。
N÷7の余りが0なら今日と同じ曜日
今日が月曜日だとして…
余りが0…月
余りが1…火
余りが2…水
…
余りが6…日
では問題で試してみましょう
4-1:日後と曜日
解説
÷7の余り0が木曜日になります。
86÷7＝12…2 より、木(0)・金(1)・土(2)で土曜日と分かりました。
日付→日数・曜日
後の日付と曜日
今日より後の日付の曜日を聞かれる問題です。例題をどうぞ
4-2:後の日付と曜日
解説
6月13日は3月3日の何日後ですか？
3月の残り(31-3=28日)+4月(30日)+5月(31日)+6月(13日)=102日後
では、何曜日になりますか？
102÷7=14…4 より
木(0),金(1),土(2),日(3),月(4) で月曜日
このように指定された日付の曜日は2ステップで求めます。
❶指定日付が起算日の何日後か計算する
❷÷7して余りを調べる
余りが0なら起算日と同じ曜日になる
(例)3/3が木曜日のとき６/13は何曜日か？
❶6月13日は3月3日の
(31-3)+30+31+13=102日後
❷102÷7=14…4 より
木(0)金(1)土(2)日(3)月(4) で月
雑学として有名な「3/3と5/5と7/7は同じ曜日になる」のもこれらの日付の間の日数が7の倍数(ともに63日)で余りがゼロになるからです。
前の日付と曜日
前の場合は、余りが0なら同じ曜日、余りが１なら前の曜日という具合に「前に戻る」ことに注意します。
N÷7の余りが0なら今日と同じ曜日
今日が月曜日だとして…
余りが0…月
余りが1…日
余りが2…土
…
余りが6…火
練習してみましょう
4-3:前の日付と曜日
解説
●2022年はうるう年ではない
➊7月21日は1月1日の 21(7月)+30(6月)+31(5月)+30(4月)+31(3月)+28(2月)+30(1月)=201日前
❷201÷7=28…5 より 木(0),水(1),火(2),月(3),日(4),土(5) で土曜日です♪
分かりましたか？
離れた日付(○年後の○/○)の曜日
平年は1年=365日なので、365÷7=52…1より、翌年の同日は曜日が1個後ろにずれる
うるう年は1年=366日なので、366÷7=52…2より、翌年の同日は曜日が2個後ろにずれる
●平年(365日)
→365÷7=52…1 より 1つ後にずれる
●うるう年(366日)
→366÷7=52…2 より 2つ後にずれる
これを利用すると○年後の同日の曜日は簡単に出せるので、計算が大幅にラクになりますね。
例題をどうぞ
5-1a:離れた日付の曜日計算
解説
2004年5月27日から3年後の2007年8月15日までに「うるう年」の2月29日はあるか？
ありません(2004年2月29日の次は2008年2月29日)
❶ちょうど3年後の2007年5月27日は何曜日か？
1年で曜日が後ろに1つずれるので、3年では3つずれて(木→金→土→日)、日曜日
❷2007年8月15日は2007年5月27日の何日後か？
4(5月の残り)+61(6月,7月)+15(8月)=80日後
❸2007年8月15日は何曜日か？
80÷7=11…3より2007年5月27日(日曜日)より3つ後にずれて(日→月→火→水)、水曜日
うるう年を含む場合
うるう年の2月29日を含んでいる場合は、日数が1日増えるので、曜日がさらに1つ後にずれます。
例題をどうぞ
5-1b:離れた日付の曜日計算
解説
●2004年5月27日から10年後の2014年8月15日までの間に「うるう年」の2/29は何日あるか？
2004/2/29の後は、2008と2012の2回ある。曜日を更に2日後ろにずらすことを忘れずに！
❶2004年5月27日(木)からちょうど10年後の2014年5月27日は何曜日か
10年後なので、平年分の10日とうるう年の2日の計12日後ろにずらして(12÷7=1…5より5日ずらすのと同じ)木→金→土→日→月→火で火曜日
❷2014年5月27日(火)から2014年8月15日は何日後か
4(5月の残り)+61(6月,7月)+15(8月)=80日後
●2014年8月15日は何曜日か？
80÷7=11…3より2014年5月27日(火)から3つ後ろにずらして(火→水→木→金)金曜日
誘導なしの練習問題を解いてみましょう
(2022.8.11作成中)
はるか未来
数百年後の未来の曜日を計算
例題
2022年2月21日が月曜日のとき次の日付は何曜日か？
(1)100年後(2122年)の2月21日
100年後でもうるう年を書き出してもよいでしょうが、計算で出してみましょう
→土曜日
(2)1000年後(3022年)の2月21日
1000年にもなると計算するほうがラクになります。
→木曜日
西暦3000年はどんな世界になっているのか、想像もつきませんが…(アーサー・C・クラーク「3001年終局への旅」」)
1つの日付と日数の問題
この章では、日暦算の2つのタイプのうち
●2つの日付を使った問題
(例)2001年1月1日から数えると2001年12月25日は何日後ですか？
(例)2001年1月1日が月曜日だとすると、2001年の12月25日は何曜日ですか？
●1つの日付(起算日)に日数を加える問題
(例)2001年1月1日の100日後は何月何日何曜日ですか
2番目のタイプを説明します
○日後は何月何日か
日付を求める計算
大きい日数の場合
○日後は何曜日か
日数→日付・曜日
大きい日数
○回目の□曜日
○日後は何月何日か
爽茶日付を求める計算
たとえばこんな問題です
6-1:日付を求める
日数を求める場合は月の日数を足していきましたが、今度は反対に日数を分解していきます。
6-1:日付を求める
解説
4月の残りが30-17=13日
つまり4/17の13日後は4月末日の4/30です
次の5月は大の月なので、プラス31して13+31=44日後が5/31です
これを、目標の87日を越えないギリギリまで続けます。
13(4月)+31(5月)=44 ←44日後は5/31
13(4月)+31(5月)+30(6月)=74 ←74日後は6/30
13(4月)+31(5月)+30(6月)+31(7月)=105 ←105日後は7/31
7月末まで足すと87を越えてしまうので、最後の7月は合計が87になる数13を足して…
87=13(4月)+31(5月)+30(6月)+13(7月) となります。
これは、4/17の87日後は 7月13日 であることを意味します♪
別解
「分解する」のが分かりにくい場合は「数を引いていく」と考えても良いでしょう。
87-13(4月の残り)=74
74-31(5月)=43
43-30(6月)=13
31より小さくなったので引き算をストップ
6月まで引いたので、この13は7月の日数で、7月13日
この日付計算は正直言って面倒くさいですが、単純な計算なので慣れて得点源にしてしまいましょう！
→Nから
「今月の残り日数」
「次の月の日数」
「その次の日数」…
を残りが31(次が大の月)か30(次が小の月)
以下になるまで引いていって、
残った日数MがN日後の日付
(例)4/17の87日後は何月何日か
→❶4月の残り30-17=13日を87日から引いて
残り74日
→❷次の5月の31日・6月の30日を74日から引いて残り13日
31(次の7月が大の月)以下なので引き算をストップ
→❸次の月が7月なので、N(87)日後の日付は7月13日
練習問題をどうぞ
6-1:日付計算
ヒント
西暦が書いてあるということは…
解説
1月の残りは31-16=25日
また2020は4の倍数なのでうるう年になり2020年の2月は29日あります
以上の2点に気をつけて、残りが31以下になるまで146から引き算をしていきます。
146-25(1月)=121
121-29(2月)=92
92-31(3月)=61
61-30(4月)=31
残りが31になり次の5月は大の月なので、引き算をストップします
1/6の146日後は、5月31日と分かります
大きい日数の場合
「500日後」「1000日後」のような非常に大きい日数を加える場合は「月ごとに分解する」方法では面倒臭すぎます。
そこで、(うるう年の2月が含まれない場合)1年=365日なので「365日後は同じ日付になる」ことを利用します。
普通の年しか無い場合
例題で解き方を理解しましょう
6-2:大きい日数後の日付
ヒント
368日=365+いくつでしょうか？
解説
366÷365=1…3 つまり368=365+3なので、368日後は1年と3日後と考えられる
1年後は翌2002年1月1日で、その3日後は2002年1月4日です
分かりましたか？では練習問題をどうぞ
6-2-1:大きい日数後の日付
解説
500÷365=1…135 より1年と135日後(3年後までうるう年なし)
翌2022年2月14日の135日後は 14(2月)+31(3月)+30(4月)
+31(5月)+29(6月) より6月29日。
うるう年を含む場合
うるう年の2月を含む場合は、1年=366日になるのに注意します。
例題を解いてみましょう
6-2-2:大きい日数後の日付
解説
368÷365=1…3 ですが、うるう年の2004年の2月29日を含むため、1年=366日になるので、368=366+2 と分解して、1年と2日後と考えます。
よって、1年後は2005年1月1日で、その2日後の2005年1月3日が答えです。
分かりましたね？もっと大きな日数で練習問題をどうぞ
6-2-2:大きい日数後の日付
解説
翌々2020年がうるう年です。
1000÷365=2…270 なので2年と270日なのですが、270日を分割するのは面倒です。
そこで、1000=365×3-95=365+366+365-96 より3年と96日前を求めると簡単ですね。
3年後2021年3月14日の96日前は 14(3月)+28(2月)+31(1月)+23(前年12月) 31-23=8より2020年12月8日です
分かりましたか？
○日後は何曜日か
爽茶日数→日付・曜日
日数を指定された場合、曜日は÷7の余りで出せるので、さらに日付計算を行い合わせて答えます。
7-1:日付と曜日計算
解説
87日後は、87÷7=12…3 なので、金(余り0),土(1),日(2),月(3)より月曜日と分かります
さらに、4月の残りが30-17=13日 で、87=13(4月)+31(5月)+30(6月)+13(7月) と分解できるので4/17の87日後は 7/13
合わせて7/13(月)と分かりました♪
この日付計算が面倒くさいのはしょうがないですね…
(日付の計算)
→Nから「今月の残り日数」「次の月の日数」「その次の日数」…
を残りが31(次が大の月)か30(次が小の月)以下になるまで引き、
残った日数MがN日後の日付
(曜日計算)
→N÷7の余りが0なら今日と同じ曜日
(例)4/17(月)の87日後は何月何日何曜日か
(日付計算)
❶4月の残り30-17=13日を87日から引いて
残り74日
→❷次の5月の31日・6月の30日を74日から引いて残り13日
31(次の7月が大の月)以下なので引き算をストップ
→❸次の月が7月なので、N(87)日後の日付は7月13日
(曜日計算)
87÷7=12…3 より0(月),1(火),2(水),3(木)
→木曜日
(解答)
7月13日木曜日
練習問題をどうぞ
7-1:日付と曜日計算
ヒント
西暦が書いてあるので…
解説
113日後は113÷7=16…1より、月(余り0),火(1)なので火曜日です
さらに、翌2020年はうるう年なので2月が29日まであるのに注意して113を分解すると
113=19(11月)+31(12月)+31(1月)+29(2月)+3(3月) なので3/3です
合わせて3/3(火)と分かりました。
大きい日数
365より大きい日数は、上で見たように「365または366+余りの数」の形に分解して計算をラクにしましょう
練習問題として、上で解いた練習6-2
6-2:大きい日数後の日付
この続きとして曜日を求めてみましょう
7-2:大きい日数後の日付
解説
500÷365=1…135 より1年と135日後(3年後までうるう年なし)
翌2022年2月14日の135日後は 14(2月)+31(3月)+30(4月)
+31(5月)+29(6月) より6月29日。
また500÷7=71…3より
500日後は0日→1月→2火→3水。
合わせて2022年6月29日(水)
解説
翌々2020年がうるう年。
1000=365×3-95=365+366+365-96 より3年と96日前を求める。
3年後2021年3月14日の96日前は 14(3月)+28(2月)+31(1月)+23(前年12月) 31-23=8より2020年12月8日。
また1000÷7=142…6 より1000日後は0水→1木→2金→3土→4日→5月→6火曜日。
合わせて2020年12月8日(火曜日)
曜日と回数の問題
日付を出す
「何日後」という数ではなく、「○曜日」と指定された日付を出すこんな問題です。
8-1:曜日指定の日付計算
1回目の水曜日は簡単に出せそうです。
そして、7日後、14日後…と7の倍数日後は同じ曜日になるので、10回目の水曜日は1回目の水曜日の何日後かも分かりそう
あとは日付計算で出来そうですね？
では、解いてみましょう
8-1:曜日指定の日付計算
解説
1回目の水曜日の日付は？
1回めの水曜日は1(月)→2(火)→3(水)で1/3
10回目の水曜日は、その何日後？
2回目の水曜日は1/3の7×1=7日後、3回目は7×2=14日後…10回目の水曜日は1/3の7x9=63日後になります。(10回目がx9なのは植木算の木と間の数の関係と同じです)
その日付は？
ここからは日付計算で63を分解すると、63=28(1月)+28(2月)+7(3月)よって10回目の水曜日は3/7と分かります
→1回目の○曜日の(N-1)回後
=7x(N-1)日後
(例)1/1が月曜日の10回目の水曜日
→1回目の水曜日1月3日の7x(10-1)=63日後
63=28+28+7より3月7日
誘導なしの練習問題をどうぞ(2022.8.21作成中)
回数を出す
反対に日付から回数を出すこういう問題もあります
8-2:日付の曜日と回数
まず5/20が何曜日か求めてから、その曜日のはじめの日付を出す、という順番で解きましょう
8-2:日付の曜日と番目
解説
5/20は1/1の何日後で何曜日ですか？
30(1月残り)+28(2月)+31(3月)+30(4月)+20(5月)=139日後
139÷7=19…6 より 金(0)→土(1)→…木曜日(6)
その曜日の最初の日はいつで、5/20はその何日後ですか？
この年の最初の木曜日は1/1(金)→1/2(土)→…1/7(木)
1/7は1/1の6日後なので、5/20は1/7の 139－6=133日後
以上より答えは？
133=7×19なので、5/20は最初の木曜日である1/7の19週間後で20回目(植木算の木と間の関係)
誘導なしの練習問題をどうぞ(2022.8.21作成中)
日付自体の問題
爽茶合計を求める
同じ曜日になる日付を合計したりする、こんな問題です
9-1:日付自体の問題
ある月において同じ曜日になる日付は、最初の日付から7づつ増えて行きます。
例えば、ある月の4日が最初の月曜日なら、次の(二番目の)月曜日は4+7=11日、三番目は11+7=18日、最後の四番目は18+7=25日になります(25+7=32になってしまうので、この問題では5番目はありません)
この性質を利用して例題を解いてみましょう
9-1:日付自体の問題
解説
土曜日の日付は1,8,15,23,31
日付の合計は1+8+15+23+31=80
ヒント
最初の水曜日をまず出してしまう
解説
1(土),2(日),3(月),4(火),5(水)より、最初の水曜日は10/5
日付の合計は5+12+19+26=62
このように、同じ曜日は4日の場合と5日の場合があることに気をつけましょう。
(最初の日付をNとしたとき…)
●同じ曜日が4日の場合
N+(N+7)+(N+7+7)+(N+7+7+7)
=(Nx4)+(7×6)
●同じ曜日が5日の場合
N+(N+7)+(N+7+7)+(N+7+7+7)+(N+7+7+7+7)
=(Nx5)+(7×10)
合計を利用する
逆に合計が与えられる問題はこうなります
ある月の日曜日の日付の合計が58だとすると1日は何曜日か
この場合日曜日が何日あるか分からないので、4回だと思って「(Nx4)+(7×6)=合計」の逆算を解いてみましょう
(例題)
(1)ある月の日曜日の日付の合計が58だとすると1日は何曜日か
最初の日曜の日付をNとしてNx4+(7×6)=58 の逆算を解くとN=4日
4日が日曜日なので、さかのぼると4(日)→3(土)→2(金)→1(木)で、1日は木曜日
練習問題をどうぞ
練習
ある月の火曜日の日付の合計が80だとすると1日は何曜日か
最初の火曜の日付をNとしてNx4+42=80 の逆算を解くとN=9.5でオカシイ!
月5回としてNx5+70=80 の逆算を解くとN=2。さかのぼって1日は月曜日
忘れたくない！という方へ
この長い記事を最後まで理解できた方は素晴らしいです！
ただ…一旦理解しても、他の分野を学習している間に記憶が薄れてしまいます。特に算数が苦手な方は「忘れて」しまうのも珍しくありません。
(参考)なぜ「忘れてしまう」のか？
実は、「忘れてしまう」と言っても頭の中から消えるわけではありません
誰でも、何かを学ぶ=新しい知識を「頭の棚」に入れると古い知識はちょっと奥に隠れますが、算数が得意な人は無意識に「頭の棚」を整理して古い知識も取り出せるようにしているので「忘れる」ことがありません。
一方、算数が苦手な人は整理が出来ないまま知識を詰め込むので古い知識はどんどん奥に追いやられ、時間が立つと取り出せくなる=「忘れてしまう」のですね…
だから、算数が苦手な人は、新しく学ぶだけでなく、意識的に頭を整理しないといけません。でも、どうやって整理すればいいのか？それが「復習」なのですね
今まで学んだ知識を広く取り出すことで、知識が取り出しやすいように頭が整理されて「取り出せない！」=「忘れた」ということが無くなっていくのです♪
こういうわけで、算数が苦手な人は新しい知識を学ぶだけでなく、定期的に復習しないといけないのです！
とはいえ、塾や習い事で忙しくて復習の時間がとれないし、復習に何を使えばいいの？。という人も多いでしょう。
そこで東大卒講師歴20年の図解講師「そうちゃ」が生徒さんの復習用に作成している教材を再構成デジタル化して「そうちゃ式 復プリ」として提供します♪(→復プリの紹介記事)
この記事のプリント「日暦算まとめ」は / まで無料でダウンロードできます。
「そうちゃ式復プリ販売所」でダウンロードして下さい。
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!