○つるかめ算まとめ(この記事)
◆個数の取り違え
◆マイナスあり(弁償算)
◆三量のつるかめ算(拘束式)
◇いもづる算
◆三量のつるかめ算(非拘束式)
「つるかめ算って何?」どうやるの?」という小学校低学年の方から、「受験に向けて応用問題を解きたい」という中学受験生の方まで、全員お任せ下さい。
つるかめ算は他の分野にもつながる「解法の宝庫」で、マスターすれば受験算数全体の実力アップ間違いなし
この「まとめ記事」では、東大卒講師歴20年の図解講師「そうちゃ」がつるかめ算の基礎から応用まで分かりやすく説明します。
この記事は非常に長いです。目次をクリックして好きな箇所から読んでも良いでしょう。
例題X-3(拘束型の3量つるかめ)の問題・解答が誤っておりました。大変失礼しました。以後このようなことが無いよう注意致します…
(dom様にご指摘いただきました。ありがとうございました)
つるかめ算とは
どういう問題か
ニ種類以上の物の単価と合計個数・合計金額から、各種類(品目)ごとの個数を求める問題です。(参考:ウィキペディアの説明)
0-0:つるかめ算の例
肉まんとピザまんをそれぞれ何個ずつ買ったか?
ここでは「肉まん」「ピザまん」という2品目の単価「80円」「100円」と合計個数「20個」と合計金額「1860円」という4つの数値から、「肉まん」「ピザまん」それぞれの個数を求めます。
2つの解法
つるかめ算の解き方には大きく2つ「面積図を使う」と「面積図を使わない=置き換え(おきかえ)法」があります。
見た目が違いますが中身は同じなので計算式は全く同じです。
「面積図」が有名なのですが「置き換え法」も重要なので、中学受験生は両方できるようにして下さい
どちらの解法が良い?
「置き換え法」の方が使いやすく8割以上の問題を解くことができます。
一方「面積図」は描くのが少し難しいですが、「置き換え法」では難しい問題を解くことができます。
そこで、はじめて見る問題を考える際は「まず置き換え法で考え、だめな場合は面積図(それでもダメなら後回し・捨て問)」というのが良いでしょう
小まとめ
●ニ種類以上の物の単価と合計個数・合計金額から、各種類(品目)ごとの個数を求める問題
(例)1個80円の肉まんと1個100円のピザまんを合計20個買ったら合計金額が1860円だった。肉まんを何個買ったか?
まず「置き換え法」から見ていきます
基本解法1:置換え法
表を用いたりして解く方法。
実質的に「差集め算」の考え方を用いている。
AB二種類の品物を買うときの手順
- 全部Aとして「仮の合計」を計算する
- 仮の合計と実際の合計との「合計の差」を出す
- AとBの「1個の差」を出す
- 「合計の差」を「1個の差」で割ってBの数を求める
例題をどうぞ
1-1:つるかめ算(置き換え法)
ピザまんと肉まんをそれぞれ何個ずつ買ったか
解説
➊「仮の合計」を出す
20個全部が肉まんだとすると100×20=2000円(仮の合計)になるはず
| 全て肉まん | … | 実際 | ||
| ピザまん (金額) |
0個 (0円) |
? | ||
| 肉まん (金額) |
20個 (2000円) |
20-? | ||
| 合計金額 | 2000円 (仮の合計) |
1860円 |
➋「合計との差」を出す
実際は1860円なので2000-1860=140円の差(合計の差)がある
➌「一個の差」を出す
ここで肉まん20個のうち1個をピザまんに変えると100-80=20円安くなる(1個の差)ので、合計も2000円から20円安くなって1980円になる。
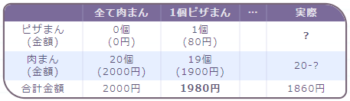
| 全て肉まん | 1個ピザまん | … | 実際 | |
| ピザまん (金額) |
0個 (0円) |
1個 (80円) |
? | |
| 肉まん (金額) |
20個 (2000円) |
19個 (1900円) |
20-? | |
| 合計金額 | 2000円 | 1980円 | 1860円 |
❹「何個取り替えるか」を出す
何個ピザまんに変えれば良いか考えると、合計の差140円を1個の差20円で割った7個と分かる。
つまりピザまんが7個で肉まんは20-7=13個になる。
| 全て肉まん | 1個ピザまん | … | 実際 | |
| ピザまん (金額) |
0個 (0円) |
1個 (80円) |
7個 (560円) |
|
| 肉まん (金額) |
20個 (2000円) |
19個 (1900円) |
13個 (1300円) |
|
| 合計金額 | 2000円 | 1980円 | 1860円 |
実際に計算して確かめると、ピザまん80円×7個+肉まん100円×13個=560円+1300円=1860円になっている。
「つるかめ表」
コンパクトな計算表「つるかめ表」を作ってみた。
単価の差
20円
↘
(80円)
(100円)
金額
肉まん
(0円)
(2000円)
2000円
買い方
()
()
1860円
140円
テスト版
| つるかめ表 | 全て 肉まん |
実際の 買い方 |
|
|
↗ |
ピザまん 80円 |
0個 (0円) |
?個 合計の差 ÷ 単価の差 |
| 肉まん 100円 |
20個 (2000円) |
20-?個 | |
| 合計 代金 |
仮の 合計 2000円 |
実際の 合計 1860円 |
|
| ↖合計の差↗ 140円 |
|||
確認テストをどうぞ
1-1:つるかめ(置き換え)
ヒント
①仮の合計」→②実際の合計との差→③1人の差→②÷③ の手順で♪
解説
11人全員が子供だと花火の合計は5×11=55個になるはず(仮の合計)
実際は43個なので55-43=12個の差がある(合計の差)
子供を1人だけ大人に変えると花火の数は5-2=3個少なくなる(1人の差)
合計の差12を一人の差3で割ると12÷3=4なので、4人大人に変えれば良い。
つまり、11人のうち大人は4人と分かる。
詳しくは「面積図を使わずにつるかめ算を解く」を見て下さい。
基本解法2:面積図
「L字型の面積図」を用います。
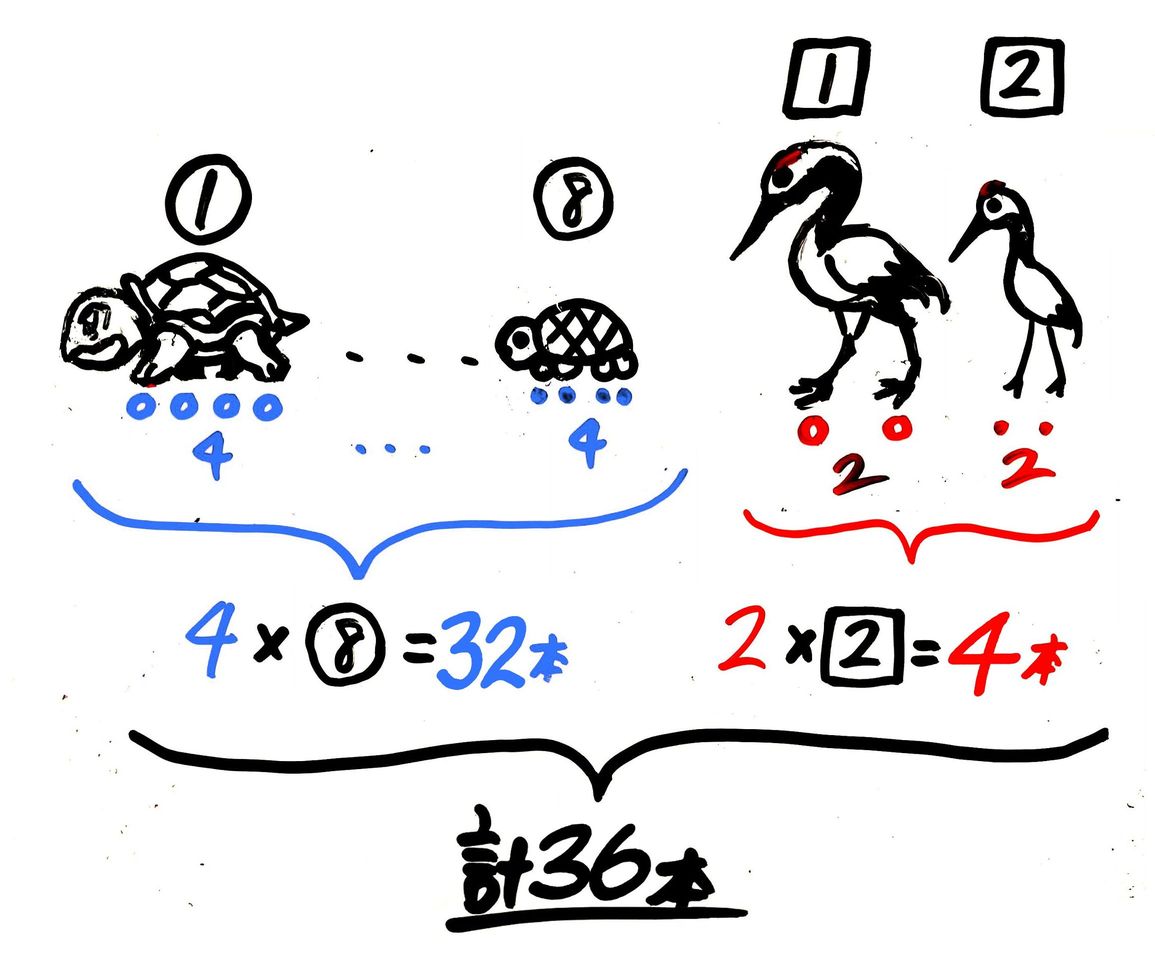
(例)鶴と亀が合わせて10匹、足が合計26本の時、
亀は何匹いるか?
- L字の面積図を書き、大きな長方形の面積を出す
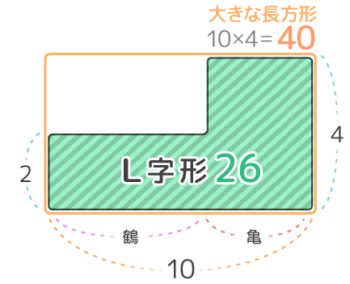
- 長方形–L字で欠けの面積を出す
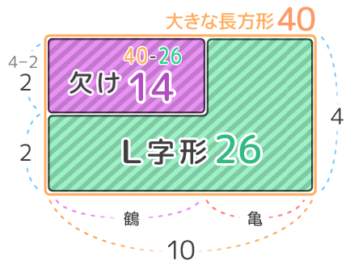
- 欠けの面積÷縦で横の長さを求め
問いに答える(終了)
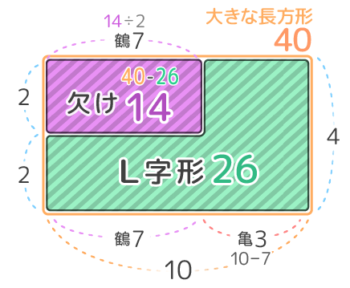
計算そのものは面積図を使わない解法と全く同じです。
確認テストをどうぞ
詳しくは「面積図でつるかめ算を解く」を見て下さい。
他の分野でのつるかめ算の利用
面積図を使う問題はつるかめ算の考え方で解けることがあります
平均とつるかめ算
度数分布表の問題
仕事算とつるかめ算
途中で「ペース」を変える問題
図形とつるかめ算
台形を分割する問題
X-1:図形とつるかめ
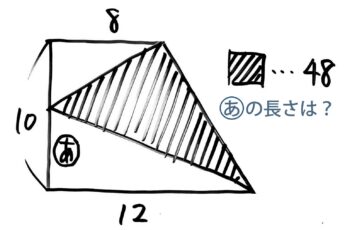
解説
練習問題
速さとつるかめ算
途中で速さを変える場合はつるかめ算で解けます
 爽茶
爽茶差(代金差)のつるかめ算
合計代金ではなく品目ごとの代金の差が示される、こんな問題です
5-1:差のつるかめ算
合計代金が分からず、品目ごとの代金差が分かります(だから「代金差のつるかめ算」です)
どのように解いて良いか分からない場合は、基本の「置き換え法」で解きましょう
5-1:差のつるかめ算
解説
一番最初の置き換え法を思い出して、全部アンパンの場合の品目ごとの金額の差を出してみると
アンパンの代金:80×20=1600\
クリームパン〃:100×0=0\
代金の差は1600\ と分かります(仮の代金差)
次にアンパン1個をクリームパンに変えると、アンパンの代金が80円減ってクリームパンの代金が100円増えるので、代金の差は180円減少して1420円になります。
このように、クリームパンを1個増やすと代金差は180円減るので、仮の代金差1600円から実際の代金差700円へと900円減らすためには900÷180=5個クリームパンにすれば良いと分かります。
15個,クリームパン5個
以上の解き方をまとめるとこうなります。
→AB二種類の品物を買ったときの、
品目の代金差が示される問題
(例)80円のAと100円のBを合計20個買ったら
Aの代金が700円高かった
- 全部Aとして「仮の代金差」を計算する
(例)80×20-100×0=1600 - 仮の代金差と実際の代金差との「代金差の差」を出す
(例)1600-700=900 - 「Aの単価+Bの単価」を出す
(例)80+100=180 - 「代金差の差」を「Aの単価+Bの単価」で割ると
Bの数が求められる
(例)900÷180=5→Bは5個
確認テストをどうぞ(2022.7.2作成中)
マイナスがある場合(弁償算)
AB二種類の品物を買うときの手順
- 全部プラスとして「仮の合計」を計算する
- 仮の合計と実際の合計との「合計の差」を出す
- プラスとマイナスの「1個の差」を出す
- 「合計の差」を「1個の差」で割って
マイナスの数を求める
仕組みと解き方
「クイズに正解するとお金をもらえるが、不正解だと罰金をとられる」というようにプラスとマイナスがある場合。
正解した場合と不正解の場合の「差」を考えます。
例えば500円持っているA君がクイズに正解すると100円もらえるが不正解だと30円の罰金を取られる(!)場合
1問目を正解すると500+100=600円になりますが、不正解だと500-50=470円になります。
したがって正解と不正解では、600-470=130円の差が生まれます。100-30ではなく100+30になるということです。
あとは「置き換え法=差集め算」の考えで、全部正解(プラス)の場合の仮の合計を出し、実際の合計との合計の差を出す。
それをプラスとマイナスの1個の差で割るとマイナスの個数が出る。
実際に問題を解いてみます。
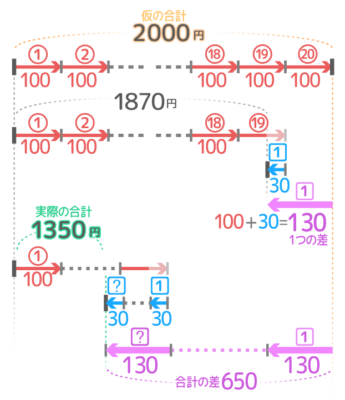
3-1:弁償算(マイナスつるかめ)
❶仮の合計を出す
全問正解の場合100×20=2000円になり(仮の合計)
❷仮合計と実際の差を出す
仮合計(2000円)と実際(1350円)との合計の差は650円。
❸プラスとマイナスの1個の差を出す
このクイズでは正解(プラス100)と不正解(マイナス30)との1個の差が100+30=130円の差がある(100-30でないことに注意)
❹マイナスの個数を求める
合計の差650÷1個の差130=5で不正解(マイナス)は5問と分かる。
確認テストをどうぞ
所持金1000円のA君が、正解すると200円の賞金がもらえ不正解だと50円の罰金を取られる30問のクイズに参加したところ、所持金は5250円になった♪何問正解したか
→( ❶仮の合計は200×30=6000円プラス )
→( ❷実際は5250-1000=4250円プラスなので、合計の差は6000-4250=1750円 )
→( ❸プラス(正解)とマイナス(不正解)の1つの差は200+50=250円 )
→( ❹マイナスの個数は1750÷250=7個 )
→( 正解したのは30-7=23問 )
所持金3000円のB君が、正解すると200円の賞金がもらえ不正解だと500円の(!)罰金を取られる10問のクイズに参加したところ、所持金は2900円に減って(!)しまった。何問間違えたか
→( ❶仮の合計は200×10=2000円プラス )
→( ❷実際は3000-2900=100円マイナスなので、合計の差は2000+100=2100円 )
→( ❸プラス(正解)とマイナス(不正解)の1つの差は200+500=700円 )
→( ❹マイナスの個数は2100÷700=3個。間違えたのは3問 )
2倍弁償算
2人でゲームをして、勝った方は得点し負けた方は失点する場合の2人の点差を考えます。
3-2:2倍弁償算
弁償算と同じように「50回全部をAが勝った場合」の点差と「Aが1回負けた場合」の点差を出して考えます
単純な弁償算と比べて、2人の「点差」は1回の勝ち負けで「勝ち点(3)」+「負け点(1)」=4段x2=8段の違いが生まれます。(だから「2倍」弁償算と名付けました)
練習問題(2022.7.2作成中)
次は「個数の取り違え」です
個数の取り違え
2品目を買うのに個数を逆にしてしまった、次のような場合です。
4-1:個数取り違えの例
90円のピザまんと120円の肉まんを合計20個買うのに、ピザまんと肉まんの買う個数を予定と逆にしてしまったので、予定よりも180円高くなってしまった。
ピザまんと肉まんをそれぞれ何個ずつ買う予定だったか
代金差が発生する仕組み
まず、取り違えで代金に差が発生する仕組みを理解して下さい。
2品目を同じ数買う場合、例えば30円のガム10個と50円のアメ10個を買う場合は「取り違え」が起きません。
取り違えが起きるのは、買う個数に違いがあるからです。よってアメとガムの個数の違い(差)に注目する必要があります。
例えば、30円アメ12個と50円のガム8個を買う予定で、個数を逆にしてしまった場合を考えます。
下のような線分図にしてみます。
個数が等しい(アメ8個とガム8個の)部分は、個数を逆にしても(アメ8個とガム8個なので)値段は変わりません。
個数が多いアメ4個の部分がチョコに変わることで、アメとチョコの1個の値段差20円×個数が多い4個分=80円の代金の差が発生します。
つまり、個数の違う部分で代金の差が発生します。
公式化
個数の違う部分で代金の差が発生するので、「予定と実際の代金の差」は「単価の差」×「個数の差」と等しくなります。(「置き換え法=差集め算」的に考えています)
公式にすると次のようになります。一番上を憶えましょう。
→個数の差で「予定と実際の代金の差」が発生する
●予定と実際の代金の差=個数の差×単価の差
(例)30円アメ12個と50円のガム8個を買うつもりが
個数を逆にしてしまった場合
→個数の差(12-8)×単価の差(50-30)
=4×20=予定と実際で代金に80円の差が生じる
○個数の差=代金の差÷単価の差
○単価の差=代金の差÷個数の差
一番上の式から、予定と実際の合計差を単価の差で割ると個数の差が出ると分かります。
また問題文に「合計○個」の形で書いてある個数の和と合わせて、個数の和と差が分かります。
この「和と差」を使って「和差算」でそれぞれの個数を出します。
以上より、取り違え問題を解く手順は次のようになります。
- 予定の合計代金と実際の合計代金の「合計の差」を出す
- AとBの「単価の差」を出す
- 「合計の差」÷「単価の差」でAとBの「個数の差」が出る(和は問題に書いてある)
- AとBの個数の「差」と「和」で和差算を行う
この手順で問題を解いてみます。
例題で確認♪
4-1:つるかめ取り違え
ピザまんと肉まんをそれぞれ何個ずつ買う予定だったか
➊合計代金の差を出す
予定と実際の合計代金差は180円
➋単価の差を出す
ピザまんと肉まんの単価の差は30円(1つ取り違えると30円の差がでる)。
➌個数の差を出す
180÷30=6でピザまんと肉まんの個数の差は4個。
また、予定よりも高くなっているのは、予定では単価が低い方=ピザまんの方が多かったから。
問題文に合計は20個と書いてあるので、和が20個、差が6個(ピザまんの方が多い)です。
➍和差算を行う
和20差6で和差算を行い、ピザまん13個,肉まん7個
6個
小(肉まん)=(和20ー差6)÷2=7 と分かる
練習問題で定着!
確認テストをどうぞ
35円の桜アメと50円の梅アメを合計23個買い、レジに行って1000円札を出した。おつりが5円もらえる予定だったが、アメの個数を逆にしてしまったので40円足りなくなってしまった。それぞれ何個ずつ買う予定だったか
→( 予定と実際の代金の差は5+40=45円 )
→( 桜と梅の単価の差は15円 )
→( 桜と梅の個数の差は45÷15=3個(実際が高くなったので予定では安い桜が多い)、和は23個 )
→( 和23差3の和差算を解いて、小(梅)=10,大(桜)=13 )
くわしい解説を読みたい・もっと問題を解きたい人は個別記事「つるかめ算個数取り違えの問題」を見て下さい。
偽の3量のつるかめ算
3量のつるかめには2種類ある
今まで扱っていた品物は「あんまんと肉まん」「ガムとアメ」のように二種類でした。これを三種類!にするのが「3量のつるかめ算」です
「3量のつるかめ算」には、「偽の3量のつるかめ」と「真の~」のニ種類あります。
「偽の~」とは3種類の個数がバラバラに決まるのでなく条件がついている場合(拘束式)で、普通の(二量の)つるかめ算に直して解けますが、「真の~」は特別な解き方をしないといけません。
●偽の3量のつるかめ算
→2量のつるかめ算に直せる
●真の3量のつるかめ算
→直せない
「真の3量つるかめ」はこの記事の一番最後にあります。
4年の間に「偽の~」を、5年の間に「真の~」を解けるようになれば大丈夫です。
比(倍)の条件
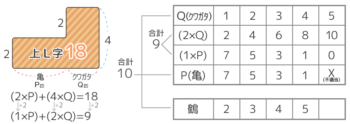
「偽の~」にはいくつかのタイプがあります。最初に比または倍の条件の場合を見てみましょう
このタイプは「平均算の面積図」の考え方を使います。
X-1:偽の3量鶴亀(比)
解説
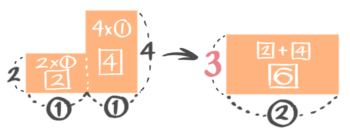
まず単純に図を書くと「3段のL字形」ができます。
このうち左のL字形の部分を平均の考え方で平らにならします。
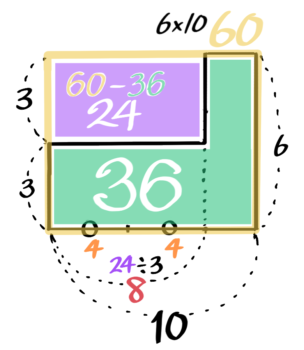
左のL字の合計を比の数字(➀:➀)を使って求めると、➀×2+➀×4=⑥です。これを長方形にすると全体の面積⑥÷横幅の②=3が高さになります。
これで三段だったL字形を二段に変えることが出来ます。
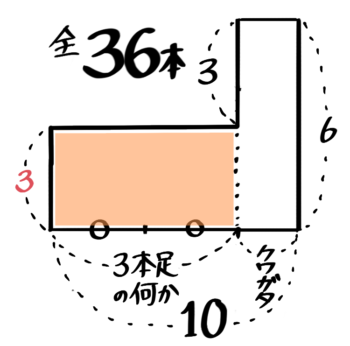
これで出来た面積図は「3本足の何かとクワガタが合計10匹で足の合計は36本」のつるかめ算になっています。
つるかめ算の面積図法でを解くと「3本足の何か」は8匹と分かります(この半分の4が鶴と亀の数)
欠けのヨコ=24÷3=8(「三本足の何か」の数)
始めの3段L字形に戻すと、鶴亀クワガタの数が全部分かりました。
他の例
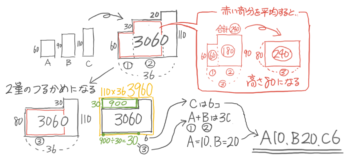
X-2:偽の3量鶴亀(比)
解説
単純に図を書くと全体が三段のL字型になってしまします。
しかし、平均の考え方でAとBの二段のL字型を長方形に直すと、全体が二段のL字型になるので、つるかめ算で解くことが出来ます。
つるかめ算を解いたらAとBも求めて、A10,B20,C6と分かります。
練習問題をどうぞ
爽くんは40円のA,50円のB,70円のCの3種類の品物をそれぞれ1個以上合わせて50個買って2720円払った。
AとBの個数の比が3:2のとき、Cを何個買ったか
ABのL字形を長方形にならすと高さ44になります
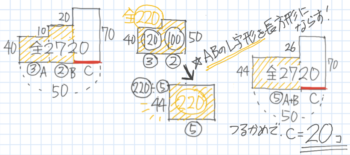
これで「44円の品物と70円の品物Cを合わせて50個買ったら合計が2720円になった」という2量のつるかめに直せました。
Cの個数を出すと、{2720-(50×70)}÷(70-44)=20個と分かります
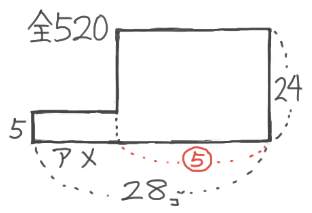
差の条件
3品目のうち2品目に差の条件が書いてある場合は、差の部分を削り取って全部の個数と全部の合計を減らします。
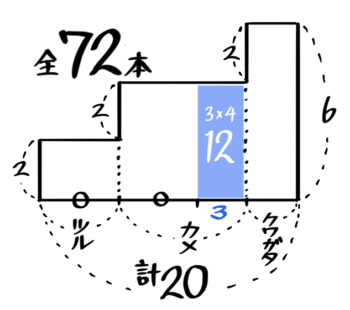
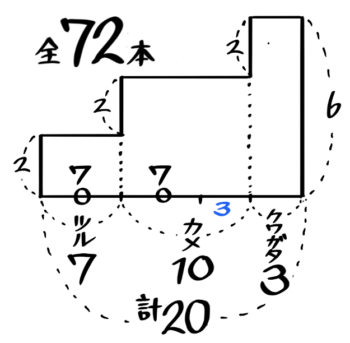
X-3:3量のつるかめ(拘束型)
解説
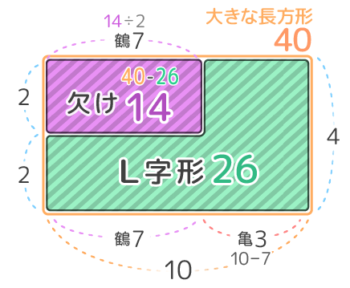
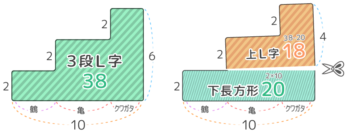
図を書くと三段のL字型になっていますが
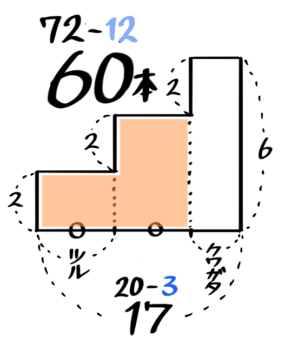
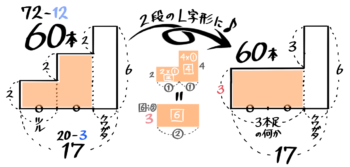
三段のL字型の図の横の長さが「3」となっている部分(面積3×4=12)をそっくり削り取り
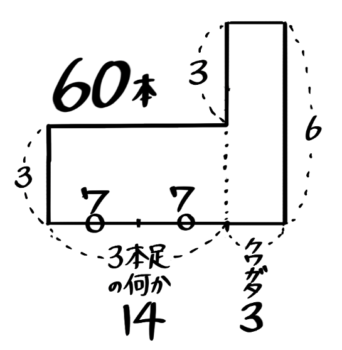
オレンジ色の2段Lを平均して長方形にすると、「3本足の何か」とクワガタが合計17匹、足の数の合計60本という通常のつるかめ算と同じになります。
これを解くと、クワガタ3匹、3本足の何か14匹とわかります。
これを最初の3段L字形に戻すと、鶴は7匹、亀は7+3=10匹と分かります♪
以上より、鶴7,亀10,クワガタ3と分かりました
練習問題をどうぞ
比(倍)と差の組み合わせ
上の2つの解き方を組み合わせます。
合計の条件(受験5年夏以降)
2つの品目それぞれの代金が等しいという条件がある場合は「逆比」を使って解きます。
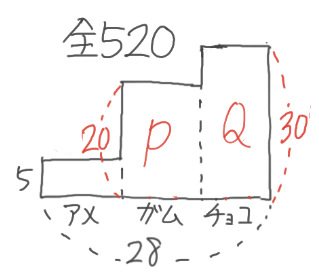
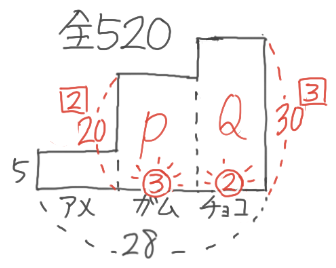
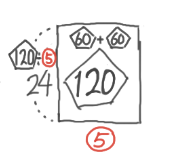
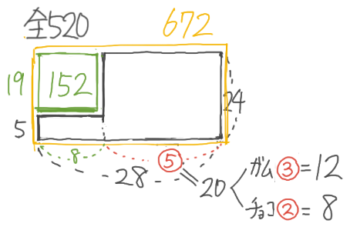
X-5:3量のつるかめ(拘束型)
解説
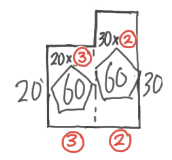
3段のL字形を書きます。ガムとチョコの代金が等しいので、PとQの面積が等しくなります
ここで、面積が等しい2つの長方形の縦の比と横の比は逆になるので、縦の比が200:300=2:3より横の比は➂:➁になると分かります。
これを利用して、ガムとチョコの部分を平らにならすと、横⑤、縦24円の長方形になり
2段のつるかめで解くことが出来ます。
アメが8個なので、⑤=20個になり、ガム➂=12個、チョコ➁=8個と分かりました。
偽の(拘束型の)3量のつるかめ算は以上です。
→3量のうち2量が特別な関係にある場合は
普通のつるかめ算に直せる
例:つる,かめ,クワガタが合計10匹、足の数は合計36本
で、つるとかめの数は同じ(←特別な関係)
- 全体を3段のL字形の面積図で書く
- 特別な関係がある2量のL字形を長方形にして
全体を2段のL字形に直す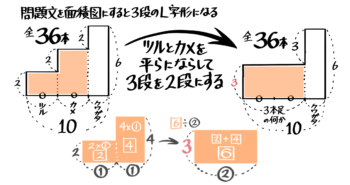 つるとかめのL字を長方形に
つるとかめのL字を長方形に - 普通のつるかめ算として解く
- 元の3段に戻して、問いに答える
➂
 →④
→④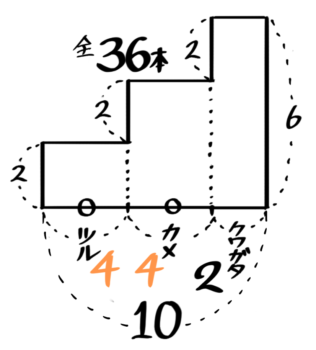 大きな長方形(60)-L字形(24)で出した欠け(24)
大きな長方形(60)-L字形(24)で出した欠け(24)
の横の長さ(8)が半分がツルとカメの数になる
真の3量のつるかめ算
真の(非拘束型の)3量つるかめ算はつるかめ算の最終形態。三種類の個数がバラバラに決まる場合です。
面積図と「いもづる算」を使って解き、答えが何通りかあることも多い面倒な問題。
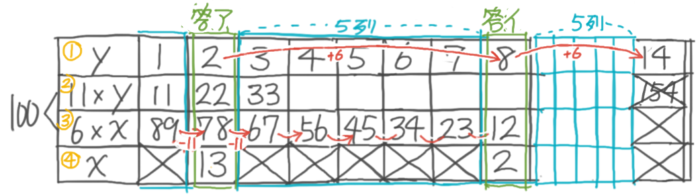
いもづる算
3量のつるかめを解く前に、下のような「いもづる算」が解けるようにならないといけない。
Y-1:いもづる算
一見すると「つるかめ算」のようですが、みかんとりんごの個数が合計が分かりません。
このような問題を「いもづる算」と言います。
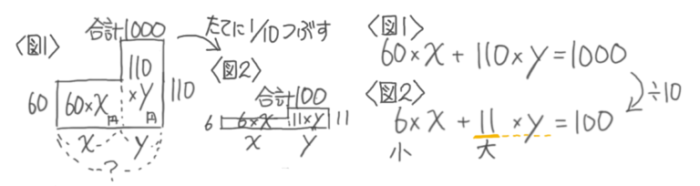
まず、みかんをx個、りんごをy個買ったとして、関係を式にすると「60x+110y=1000」になります。
この式の数字を全部10で割る(0をとる)と「6x+11y=100」になります。
この式「6x+11y=100」が成立するようなxとyを見つければ答えになります。
これらは計算でサッと出すことはできません…表を書いて、ありえる組み合わせを全部見つけます(面倒くさいですが…)。
この表は、かけられる数が多い文字(ここではy)に数字を1から順に入れたときにxが決まるかを調べる作業をそのまま項目にしています。
左から2番目の列は、y=1の時に11y=11になるので、これと合わせて100になる6x=89と分かりますが、その場合x=14.~という小数になってしまい不適切」ということを表しています。
y=2の時も同様に考えるとx=13が見つかりますが、その後はy=8まで答えが見つかりません。
ここで表全体を眺めると、y=2からy=8までの間に5列があるのが見えます。これは次の5列も答えが見つからないことを示してくれています。
したがって、その後はy=9を調べずに、5列を間にしたy=14を調べます。これが不適切なので調べは終了でs.
結局(x=13,y=2)(x=2,y=8)という2つの組み合わせが見つかり、これが答えになります。
この「いもづる算」は調べないと分からないので、受験算数でも一番面倒くさい部類に入ります。
- 個数をPQとして、関係式を作る
- 関係式の数字を同じ数で割れるなら
割って簡単にする - 表を作り、数が大きい文字から
1,2,3…と入れていく - もう一方の文字が自然数で出たら
それが解答セット - 設問に答える形で解答する
いもづる算が出来るようになったら、やっと「真の3量のつるかめ算」へ!
3量のつるかめ算へ
面積図を切り取って「いもづる算」にして解きます。
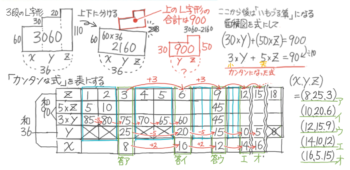
Z-1:真の3量のつるかめ算
解説
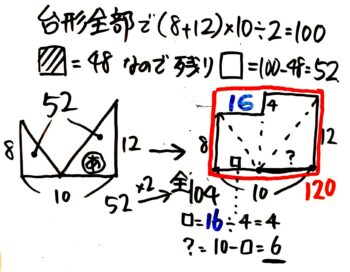
まず問題文をそのまま面積図にすると、幅が10の3段のL字形ができます(図1左)。
この3段L字で、高さが2より低い長方形(面積は2×10=20)を切り落として、亀とクワガタだけのL字型(左右の高さは2と4になる)を取り出します(図1→)。
このL字型の面積は38-210=18になるので、亀の数をP,クワガタの数をQとすると、「2×P+4×Q=18」という式が成り立つ。L字形の横幅は分からないので、ここからはさっきの「いもづる算」と同じになります。
まず「2×P+4×Q=18」の全体を2で割って簡単にすると「1×P+2×Q=9」になる。このあとは足の数が多いクワガタが1,2,3…と調べて表にしていく。
Q(クワガタ)=1の時のP(亀)を求めてみると「1×P+2×1=9」よりPは7、鶴は10-(1+7)=2
Q(クワガタ)=2の時は「1×P+2×2=9」よりP(亀)は5、鶴は10-(2+5)=3
Q(クワガタ)=3の時は「1×P+2×3=9」よりP(亀)は3、鶴は10-(3+3)=4
Q(クワガタ)=4の時は「1×P+2×4=9」よりP(亀)は1、鶴は10-(4+1)=5
Q(クワガタ)=5の時は「1×P+2×5=9」よりP(亀)は0になって不適当で、ここで調べ終了
答えは鶴は2,3,4,5の3通り(面倒くさい!)
もう一つの例
Z-2:真の3量のつるかめ算
解説
三段のL字型の下を横幅いっぱいの長方形の形で切り取り、二段のL字型にすると、二量のいもづる算になる。
表を書いて調べると、(X,Y,Z)の組み合わせは5通りあると分かります。
確認テストをどうぞ
(2021.3.17作成中)
 爽茶
爽茶●「つるかめ算」(サイパー)
●「算数の基本問題4年」(日能研)
●小4まで…和差センス(シグマベスト)
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ