「つるかめ算って面積図?を使わないと解けないの?」という小学生・保護者の方へ。
確かに面積図が有名なのですが実は面積図を使わない方法が基本なんですよ!
この記事では東大卒講師歴20年の図解講師「そうちゃ」が表を使った「置き換え法」を分かりやすく説明します。豊富な例題で定着を図れますよ!
なお、面積図を使った解き方を見たい人は「L字型の面積図を使った『つるかめ算』の解法」を見て下さい。
下の目次をクリックすると好きなところにジャンプできます。
つるかめ算とは?
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
つるかめ算と言えば、面積図を使った解法が有名ですが、実は!面積図では解きにくい問題も多いのです。
私自身、面積図を使わない解き方を最初に教えています。
まず、はじめにつるかめ算について説明すると、つるかめ算は、以下のような問題というかクイズ!です。
鶴と亀が合わせて10匹いる。
鶴と亀の足の数を合計すると26本になる時、鶴と亀はそれぞれ何匹いるか?
中学以降の数学では「連立方程式」を使って簡単に解けますが、「連立方程式」を使えない小学生は「置き換え法」を使います。
「置き換え法」には「表(ひょう)を使う」「線分図を使う(差集め算)」の2つの方法があります。中学受験をする場合、2つとも理解できると良いでしょう。
表でつるかめ算を解く
はじめに「表(ひょう)を使った置き換え法」です。もう一度問題を見ましょう。
例題1(つるかめ算)
鶴の足の数と亀の足の数を合計すると26本になる時、
鶴と亀はそれぞれ何匹いるか求めよ。
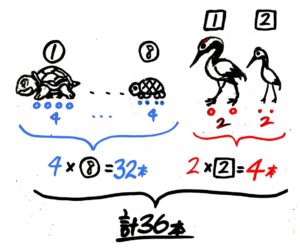
パッと答えが出ない問題に当たったら、状況を整理するのが肝心です。ここでは、10匹のうち鶴と亀の数の変化によって足の数がどう変化するのか整理してみましょう。単純なのは、10匹全部が亀(Aとします)、その反対に10匹全部が鶴(Bとします)、鶴と亀が半々(Cとします)。この3つの場合でしょう。
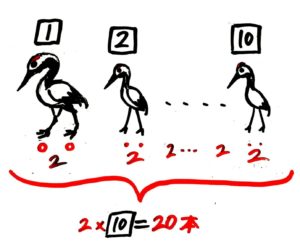
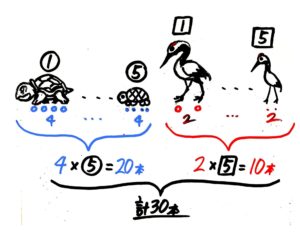
この3つの場合を表にしてみます。
| Aの場合 | … | Cの場合 | … | Bの場合 | |
| 亀の数 (足の数) |
10匹 (40本) |
… | 5匹 (20本) |
… | 0匹 (0本) |
| 鶴の数 (足の数) |
0匹 (0本) |
… | 5匹 (10本) |
… | 10匹 (20本) |
| 足の合計 | 40本 | … | 30本 | … | 20本 |
ざっと眺めると、亀が10匹から5匹、0匹と減ると合計の足の数も減っていくのがわかります。
これで状況が理解できたので、いよいよ問題を解いていきましょう。
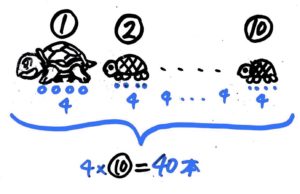
さて、はじめは答えの見当がつかないので、10匹全部が亀だとします(A)鶴としても良いですが、足の数が多い方にするのが普通です
すると足の数の合計は4×10で40本になります

ここで10匹の亀のうち1匹を鶴に取り替えたら足の数の合計はどうなるでしょうか?(このように取り替えることを「置き換え」といいます
亀4×9=36本 + 鶴2×1=2本 で合計38本になります。

↓
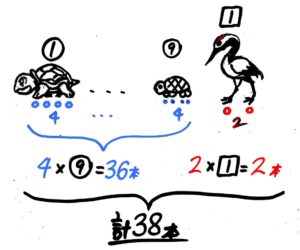
Aの場合より合計が2本減りました。表にするとこうなります。
| Aの場合 | 1匹 置き換え |
正しい 場合 |
|||
| 亀の数 (足の数) |
10匹 (40本) |
9匹 (36本) |
… | … | |
| 鶴の数 (足の数) |
0匹 (0本) |
1匹 (2本) |
… | … | |
| 足の合計 | 40本 | 38本 | … | … | 26本 |
どうして「2」本減るのかというと…亀と鶴一匹の足の差が4-2=2だからですね。
では、さらにもう1匹鶴に置き換えて亀8,鶴2にするとどうなるでしょうか
こうなります
亀4×8=32本 に 鶴2×2=4本 で合計36本。やはり合計が2本減ります。
| Aの場合 | 1匹 置き換え |
2匹 置き換え |
正しい 場合 |
||
| 亀の数 (足の数) |
10匹 (40本) |
9匹 (36本) |
8匹 (32本) |
… | |
| 鶴の数 (足の数) |
0匹 (0本) |
1匹 (2本) |
2匹 (4本) |
… | |
| 足の合計 | 40本 | 38本 | 36本 | … | 26本 |
このように、亀を1匹鶴に置き換えるたびに40,38,36,34…と足の合計は2本づつ減っていきます。
この問題では足の合計は26本なので、40,38,36,34,32…と合計が26本になるまで、鶴に置き換えてもいいですが、
ちょっとラクをしましょう!!
(^_^;)
はじめに計算したAの場合(合計40本)と問題の数字(合計26本)では、40-26=14本の違いがあります。
そして亀から鶴に1匹置き換えるごとに2本減るのですから、14÷2=7匹置き換えれば(つまり鶴7匹、亀3匹になる)いいんじゃないでしょうか?
( ・Θ・)
計算して確かめると…亀4×3=12本 に 鶴2×7=14本 で合計26本になりました!!
(^O^)
| Aの場合 | 1匹 置換 |
2匹 置換 |
7匹 置換 |
||
| 亀の数 (足の数) |
10匹 (40本) |
9匹 (36本) |
8匹 (32本) |
… | 3匹 (12本) |
| 鶴の数 (足の数) |
0匹 (0本) |
1匹 (2本) |
2匹 (4本) |
… | 7匹 (14本) |
| 足の合計 | 40本 | 38本 | 36本 | … | 26本 |
これで、答えは鶴7匹、亀3匹と分かりました!!
このように、「どちらか一方だけにした合計(40)」と「問題文に書いてある合計(26)」の合計の差(14)を出しておいて
足の数「亀(4)」と「鶴(2)」の一匹の差(2)で割ると、何匹置き換えればよいのかが分かります。
この解法を「置き換え法」と呼びましょう。置き換え法は4ステップで解いています。
- 全部亀として仮の合計を計算する
- 仮の合計と実際の合計との「合計の差」を出す
- 鶴と亀の「一匹の差」を出す
- 「合計の差」を「一匹の差」で割って鶴の数を求める
次に「線分図を使った置き換え」を紹介します。これは「差集め算」の一種です。
線分図を使って解く
今度は「鶴と亀」ではなく「中華まん」にしましょう。
例えば「1個80円のピザまんと1個100円の肉まんを合わせて20個買ったら1860円だった時、ピザまんを何個買ったか」考えます。
全部が肉まんだとすると合計は100×20=2000円です。これが「仮の合計金額」になります
(全部が肉まんの場合)
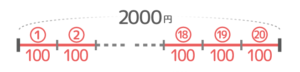
肉まんとピザまんの単価の差は100-80=20円なので、肉まんを1個ピザまんに変えると合計金額も20円安くなります。
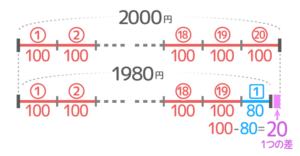
合計金額が20円安くなる。
実際の合計金額は1860円で、仮の合計2000とは2000-1860=140円の差があります(合計の差)
この合計の差140円は単価の差20円×ピザまんの個数と等しくなります。
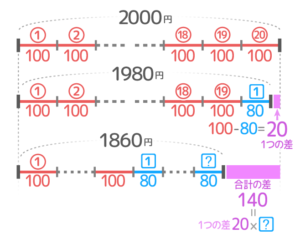
を利用すれば?が分かる
したがってピザまんの数は140÷20=7個と分かります。
今のやり方をまとめるとこうなります(表を使った場合と計算は全く同じですね)
- 全部肉まんとして仮の合計を計算する
- 仮の合計と実際の合計との「合計の差」を出す
- 肉まんとピザまんの「一個の差」を出す
- 「合計の差」を「一個の差」で割ってピザまんの数を求める
では「置き換え法」を使って問題を解いてみましょう。
つるかめ算の練習問題
表や線分図で理屈を理解できたら、ここからは計算だけで答えを出してみましょう。
例題2(置き換え法)
80円のチョコと100円のチョコを合わせて10個買ったら、代金の合計が880円だった。以下の問いに答えなさい。
- 10個全部が100円のチョコだとすると、合計代金はいくらになるか。また実際の代金の合計とは何円の差があるか?
- 100円のチョコ1個を80円のチョコに置き換えると合計代金は何円変化するか?
- 合計代金を880円にするには、何個80円のチョコに置き換えればよいか。
結局、80円のチョコと100円のチョコはそれぞれ何個か
例題と比べると「1匹で足2本」の鶴が「1個で80円」のチョコに、「1匹で足4本」の亀が「1個で100円」のチョコに変わりましたが、解き方は変わりません♪
(*^ー゚)b
先程の公式の言葉だけ変えて、こうなります。
- 全部100円チョコとして仮の合計を計算する
- 仮の合計と実際の合計との「合計の差」を出す
- 100円チョコと80円チョコの「一個の差」を出す
- 「合計の差」を「一個の差」で割って80円チョコの数を求める
それでは、順番に「合計の差」と「一つの差」を出していきましょう。
●例題2-(1)
10個全部が100円のチョコだとすると、合計代金はいくらになるか。また実際の代金の合計とは何円の差があるか?
10個全部が100円のチョコだとすると、合計代金は100×10=1000円になりますね(❶)。
そして実際の代金が880だったので、実際の合計代金との差は1000-880=120円になります(❷)。
答(1): 代金1000円,差120円
●例題2-(2)
80円のチョコに1個置き換えるごとに、100-80で、合計代金は20円変化します(❸)。
答: 20円
これで置き換え法の準備ができました。
●例題2-(3)
結局、80円のチョコと100円のチョコはそれぞれ何個か
合計の差が120で、ひとつあたりの差が20なので
120÷20=6で、80円のチョコに6個置き換えれば良い(❹)。
80円のチョコは6個、10-6 で100円のチョコは4個
答(3): 80円 6個,100円 4個
できましたか?
今度は小問の誘導なしで解いてみましょう!
(*^ー゚)b
類題2-1
❶15枚全部がメダルBだとすると重さは230×15=345gで
❷実際の重さとの差は3450-3300=15g
❸23gのメダルBを20gメダルAに1枚置き換えると、23-20で3g変化する
❹合計を3450から3300にするには、15g÷3g=5 なので、メダルAに5枚置き換えれば良い。メダルAが5枚、15-5でメダルBは10枚
答: A5枚,B10枚
類題2-2
❶20枚全部が50円玉だとすると、合計金額は50×20=1000円 なので
❷実際の合計金額との差は1000-320=680円
ずいぶん差がありますね(^_^;)
❸50円玉を10円玉に1枚置き換えると、50-10で40円変化する
❹合計を1000円から320円にするには、680÷40=17 で10円玉に17枚置き換えれば良い。10円玉が17枚 20-17で50円玉は3枚になります。
答: 10円玉17枚,50円玉3枚
ほとんどが10円玉だったんですね
(T_T)
これで面積図を使わない「つるかめ算」の解法は終了です。お疲れ様でした。
まとめとプリント

プリントダウンロード
解答/解説プリントは画像を保存できます。著作権は放棄しておりません。無断転載引用はご遠慮ください。
最初に書いたように、つるかめ算の基本問題は「置き換え法」で十分解けるので、通っている(通う予定の)塾が面積図を標準解法にしていないならば、まずは「置き換え法」で基本問題を速く正確に解けるように練習しましょう。
実際、面積図を使った場合も計算式自体は全く変わらないので、置き換え法をきちんとマスターすれば面積図を使った方法もすぐ理解出来るはずです。ご安心下さい。
 爽茶
爽茶●「つるかめ算」(サイパー)
●「算数の基本問題4年」(日能研)
●小4まで…和差センス(シグマベスト)
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ