場合の数の基本ルール「えらび方」と「ならべ方」

中学受験生で「場合の数がわからない…」という方へ。

確かに、場合の数には非常に多くの種類の問題がありますね。しかし共通して使う「基本ルール」は3個ほどしかありません！

この基本ルールをしっかり憶えてから、各種の問題に取り組めば「場合の数がわからない！」ということはなくなります。

この記事では東大卒講師歴20年の図解講師「そうちゃ」が場合の数で使う基本ルールを分かりやすく説明します。

記事を真似して例題を解けば基本ルールを定着できますよ♪

場合の数には二種類ある

場合の数には非常に多くの種類の問題がありますが、使うルールは大きく分けてこの２つです。

問題を解く時は「えらび方」か「ならべ方」かを考えれば計算方法も決まります。

確認テスト
「ならべ方」か「えらび方」のどちらか答えなさい

(2021.3.28作成中)

構成を根本的に変えようか？・例を統一する「ABCDE5人」・説明する順番は「ABCDE全員並べかえ」→「ABCDEから3人選んで並べかえ」「ABCDEから3人選ぶだけ」。これが公式を説明しやすい小山田さんの体験で、試してみるか…(30分)

ならべ方

全員を並べかえる

何人かを並びかえるやり方が何通りあるか考えます。

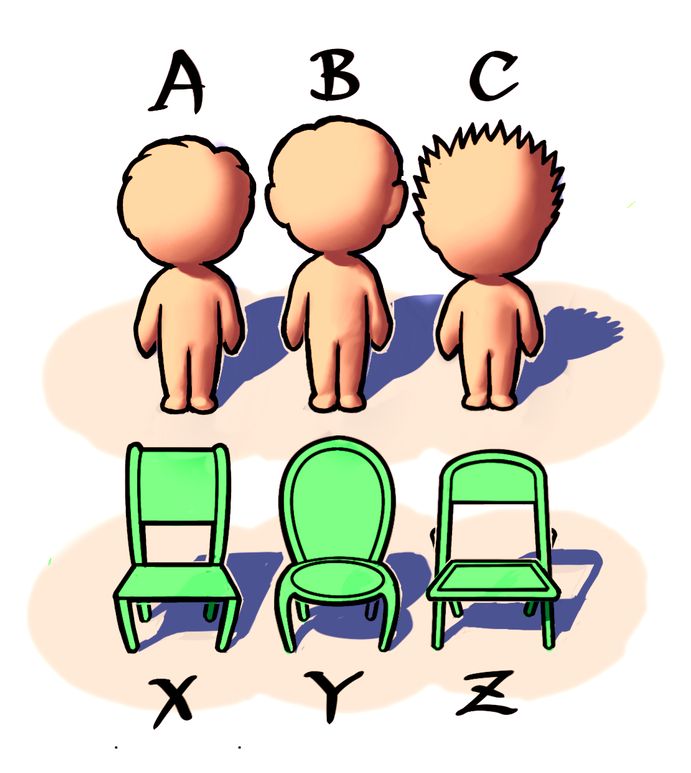
例えば、横に並んだイスXYZにABC3人を座らせる場合を考えます

書き出して調べる(樹形図)

XYZの順に誰が座るかを書き出して調べるやり方。

Xに座るのはABC3人のうち誰かなので3つの場合があります。

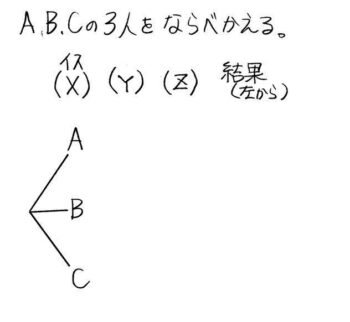
XにAが座った場合、Yに座るのはBCのどちらかです。

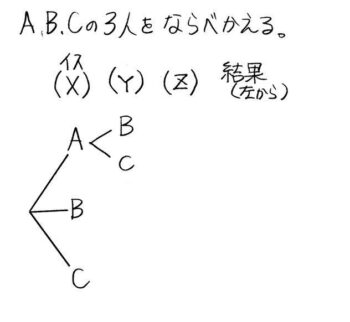
YにBが座った場合Zには自動的にCが座ります。

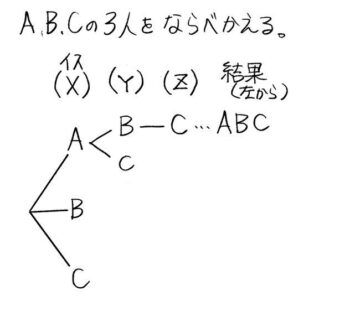
一番上に、「ABC」と並んでおり、これは「XにA,YにB,ZにC」と座ったことを意味しています。

また一番上の段にイスの名が(X)(Y)(Z)と書いてあります。これを「項目名」と呼びます。この項目を書くのを忘れないようにして下さい。

同じ様に残りを全部書くとこうなります

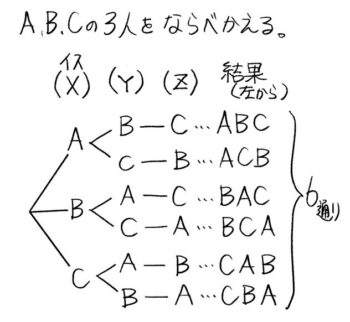
右端の「枝」の数が何通りかを示します。この場合は6通りです。

計算で出す

計算で出すこともできます。さっきの樹形図の「項目」ごとに何通りあるかを考えて、かけ算します。

Xに座るのはA,B,Cのいずれかで3通り、Yに座るのはXに座らなかった2人のいずれかで2通り、Zに座るのはXにもYにも座らなかった人で1通り

以上より、3×2×1=6通りです(樹形図と同じになりました)

小まとめ

一部をならびかえる

さっきは全員を並び替えましたが、今度は何人かをえらんで並びかえます。

例えば、横に並んだイスXYZにABCDE5人から3人を座らせる場合を考えます

樹形図

項目を書いてXから書いていきます

一番上が出来ました。

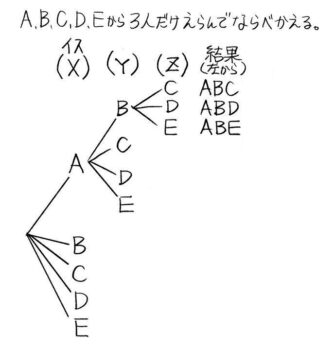
途中を省略する

同じ形と予想がつくので、人は書かずに枝の形だけを書きます。

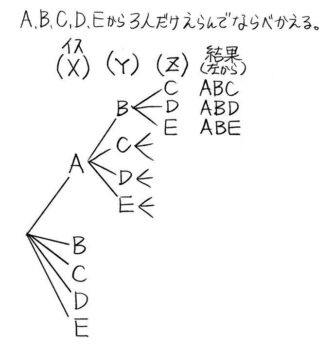
これで太い枝Aから出る細い枝は12本と分かるので、小計として12と書いておきます。

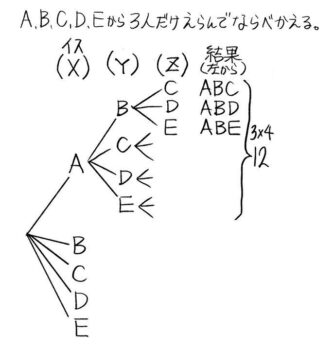
Bの下はAを同じだろうと想像がつくので、枝の形すら書かずに小計だけを書きます。

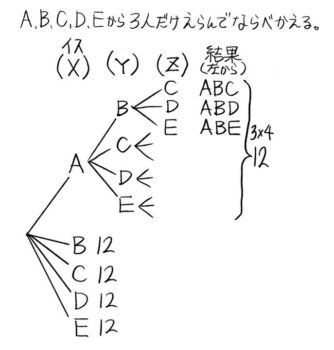
大きなカタマリが5つあって、それぞれに12本の枝があるのが分かります。

したがって12×5=60通り

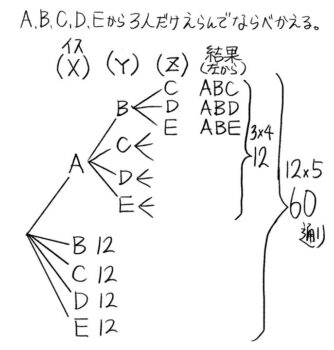
計算

5×4×3=60通り

小まとめ

ここまでのならべ方の求め方をまとめておきます。

練習問題で定着♪

作成中

えらび方

今度はABCDE5人がイスでなくカーペットで休憩します。座る場所は自由なので、誰が座るかをえらべばOKです。

他の例。帽子をかぶる。

このように場所による区別や順番が無い場合が「えらび方」です。

1人選ぶ

1人だけ座れる場合、5通り

2人選ぶ

2人座れる場合

今度は「A」「B」「C」「D」「E」5人から2人を選ぶ場合を考えます。

左から右に向かって2人を選んでいきます(「A-B」はOKですが「B-A」はダメ!です)

4+3+2+1=10通り になります。

ここまでの公式化

4種類から2種類選ぶと3+2+1=6通り
5種類から2種類選ぶと4+3+2+1=10通り なので

N個から2個選ぶ場合の数は、(N-1)+(N-2)+…+1 になると分かります。

3人以上選ぶ(裏技)

数え上げ

ABCDE5人から3人を選ぶ場合、同じように左から右へ選んでいきます(ABCは良いが、ACBやBCAはダメ)

((図))

大変ですね。

裏技

ちょっとした裏技が使える場合があります。

上の例で答えが10通りでしたが、これは「5人から2人を選ぶ」問題と答えが同じになっていました。

((図))

つまり「5人から休憩する3人を選ぶ」のと「5人から休憩しない2人を選ぶ」のは同じということです。

同様に「10人から6人選ぶ」と「10人から4人選ぶ」、「100人から99人選ぶ」と「100人から1人選ぶ」は等しくなるので、選ぶ人数が少ない方を求めれば良いのです。

この裏技を使えば、「3個以上を選ぶ」問題を「2個を選ぶ」問題にできることが結構あります。

確認テスト
8人から6人選ぶのは何通りあるか？
→( 「8人から6人選ぶ」は8-6=2なので「8人から2人選ぶ」と等しい )
→( 7+6+5+4+3+2+1=28通り )

小まとめ

ここまでの「えらび方」をまとめておきます。小4受験生まではこれだけでも良いでしょう。

3人以上選ぶ(計算)

上の裏技が使えない場合に計算で出す方法です。

例えばABCDEF6人から3人を座らせる場合です。

並べかえとの違い

ここで「一部ならべかえ」の公式を思い出します。こうでした。

この公式は使えません。

なぜなら60個のうち、同じ「組み合わせ」が入っているからです。

たとえば「ABC」の組み合わせを「ABC」「ACB」「BAC」「BCA」「CAB」「CBA」と6回数えています。

(図)

他の組み合わせも同じなので、結局「一部ならべかえ」は「えらび方」は6倍も数えてしまっている。

÷6すればよい。60を÷6した10通りが答えになります。

これは5人から2人を選ぶ場合も同様です。

5人から2人をえらんで並び替える「一部並び替え」は5×4=20通りですが

これは同じ組み合わせを2回ずつ数えている。

((図))

20÷2=10通りが正しい答え。

このように、

重複カウントの回数

重複カウントは「全部ならびかえ」の答えと同じになります。

例えば2個選ぶ場合は、重複カウントは2個全部のならびかえの数なので、2×1=2回 です。

3個選ぶ場合は、重複カウントは3×2×1=6回

4個選ぶ場合は、重複カウントは4×3×2×1=24回

これらの数が公式の分母(割る数なので)になります。

公式化

結局、どのような場合でも使える「えらび方」の公式はこうなります。公式を憶えるというよりも、(例)から式を作ることができればOKです。

基本ルールのまとめ

基本ルールが出揃ったので、まとめておきます。

練習

 

場合の数同士の関係(和と積の法則)

問題を解いていて場合の数が2つ出た場合に、その2つの数字をどうすれば答えになるのか(足すのか掛けるのか)迷うことがあります。

基本的な考え方

2つの場合の数の関係を考えて、「そして」や「かつ」ならかけ算(積)にします。上で出てきたならべ方がこちらでした。2つの場合の数が「あるいは」や「または」なら足し算(和)にします。

たとえば、長ズボンが3通り、半ズボンが2通りある場合の服装の場合の数を考えると、長ズボン「または」半ズボンを履きますね？よってズボンの履き方(ファッション♪)は和:3+2=5通りになります。

一方、長ズボンが3種類・上着が4種類の場合は、長ズボン「そして」くつを履きますね？よって服装の場合の数は積:3×4=12通りになります。

樹形図を想像しても良いでしょう。

長ズボンと半ズボンの場合はこういう図になります。

和の法則の樹形図

項目が1つだけ

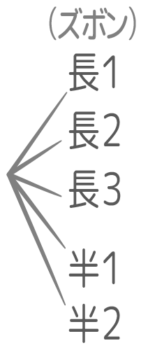
項目が(ズボン)一つしかありません。

二番目の場合はこういう図になります。項目が(ズボン)と(上着)と二つ並んでいます。

積の樹形図

項目が2つある

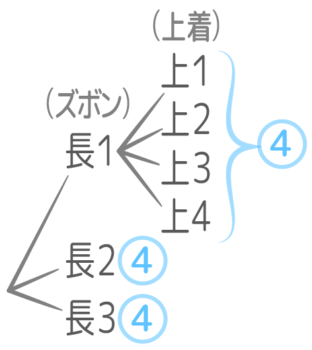
このように項目が2つになる場合は積(かけ算)になると覚えても良いでしょう。

組み合わせ

3つの場合の数が出てきた場合は、和と積を組み合わせて答えを出します。

1-1:和と積の法則

長ズボン3種類,半ズボン2種類,上着4種類で何種類のファッションができるか。

解説

ズボンは長ズボン「または」半ズボンなので「和」3+2=5通り

上着は同時に着れる「かつ」なので(積)x4になる

以上より(3+2)x4=20通り

図1:

項目は「ズボン」と「上着」の2つ

20通り

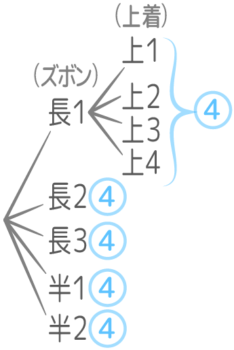
さらに条件を付け足してみましょう

1-2:和と積の法則

長ズボン3種類,半ズボン2種類,上着4種類,サングラス2種類で何種類のファッションができるか。ただし、サングラスはつけてもつけなくても良い)

解説

ズボンと上着で(3+2)x4=20通り までは先程と同じ

サングラスは「かけない」と合わせて3通りで、ズボンとも上着とも同時に着れるので「積」x3 になる。

以上から、(3+2)x4x3=60通りです

樹形図

サングラスは「つけない」
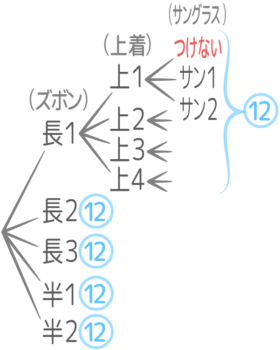
も入れて3通り

60通り

確認テスト

(2021.3.28作成中)

オリジナル教材のご案内

御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評！
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ

人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史　●時事問題(2025年)　●世界地図　●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)

その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ