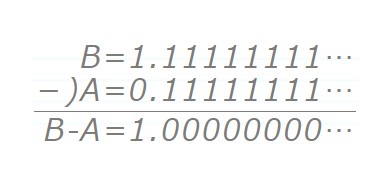小数の応用問題を解きたい」という中学受験生の方、おまかせ下さい。
東大卒講師歴20年の図解講師「そうちゃ」が問題と分かりやすい解説を用意しました！
小数点移動の覆面算(受験小4)
ある分からない数Aとその小数点を移動してできる数Bで作る計算結果からAを当てる問題。
1-1:小数の覆面算
(解説)
ある数Aは何ケタの数か分かりませんが、小数点があるのは確かなので一番簡単に思いつく小数点1ケタと整数1ケタの「a.b」としてみると、Bは「0.ab」でA-Bはこんな感じになります。
-0.ab
x.yz
「0.ab」になり、引き算の答えは
小数第ニ位までになる
A-Bの答えは小数点第二位までの数になるので、いい感じです♪
試しにAを小数点第二位までの「a.bc」にしてみると、引き算の答えが小数第三位までになってしまうのでダメです
-0.abc
w.xyz
小数第三位まで出てしまう
またAに小数点がない「a」にしてみると、引き算の答えは小数点第一位までなので、やはりダメです。
-0.a
x.y
小数第一位までにしかならない
このように、Aを「a.b」とおくのが一番良い感じなので、引き算の答えを1.35にして筆算を書き、観察します。
-0.ab
1.35
小数第二位での引き算は、小数第一位から繰り下がりで10-b=5という計算になっているので、b=5と分かります。
そして、b=5に書き変えて観察すると、小数第一位での引き算は、bが小数第ニ位への繰り下げで5-1=4になっているので、4-a=3という計算になり、a=1と分かります。
-0.ab
1.35
観察してb=5
-0.a5
1.35
観察してa=1
-0.15
1.35
1.35と確認
以上よりAは「1.5」と分かりました。
確認テストをどうぞ
ある数Aの小数点を左に1ケタ動かした数をBとします。A-B=2.43 のとき、もとの数Aはいくつですか？
→( 2.7 )
小数点を2ケタ動かすとどうなるでしょうか？
Bは「0.0ab」になり、A-Bの答えは小数点第三位までの数になるので、いい感じです。
-0.0ab
w.xyz
「0.0ab」になり、引き算の答えは
小数第三位までになる
試しにAを小数点第二位までにしてみると、引き算の答えが小数第三位までになってしまうのでダメです。
またAに小数点がない「a」のような場合も、引き算の答えは小数点第一位までなので、やはりダメです。
-0.abc
w.xyz
引き算の答えが
小数第三位まで
出てしまう
-0.a
x.y
引き算の答えが
小数第一位まで
にしかならない
-0.ab
1.35
b=5と分かる
小数第二位での引き算は、小数第一位から繰り下がりで10-b=5という計算になっているので、b=5と分かります。
b=5に書き変えて観察すると、小数第一位での引き算は、bが小数第ニ位への繰り下げで5-1=4になっているので、4-a=3という計算になっているので、a=1と分かります。
-0.a5
1.35
観察するとa=1と分かる
以上よりAは「1.5」と分かりました。
-0.15
1.35
1.35になるのを確認
確認テストをどうぞ
ある数Aの小数点を左に2ケタ動かした数をBとします。A-B=6.831 のとき、もとの数Aはいくつですか
→( 6.9 )
カードで数を作る問題(受験小4)
「場合の数(→まとめページ)」の問題の一つです。数字と小数点が書いてあるカードを並べ替えて小数を作る問題を考えます。
2-1:小数点を含むカードの並び替え
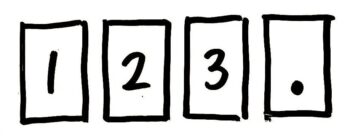
「場合の数」の順列の問題です。「樹形図」を書くと良いでしょう。
4枚のカードを並べる場所を「A」「B」「C」「D」とします。
カードの並べ方を「樹形図」で調べます。スペースの上に「項目(この場合は置く場所の名前)」を書いたら、まずAに置くカードを小さい順に書きます(小数点は置けませんね)。
次に1に続いてBに置くカードを書きます。今度は小数点も使えるので、小数点から小さい順に書きます。
さらに「1」「.」の次にC・Dに置くカードを書きます。これで一番小さい数「1.23」と二番目に小さい数「1.32」が出来ました。
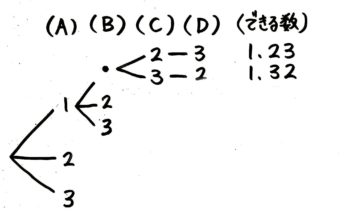
さっきの続きを書いて「1」で始まる数を全部書くと４つありました。
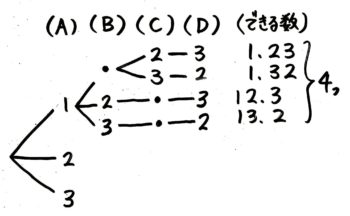
「2」で始まる数の樹形図も同じ形になるだろうと予想して省略し「4つ」とだけ書きます。
「3」で始まる数も4つあるはずですね。
(ここでは小問3に備えて書いている)
全部で4×3で12個です。
さっきの樹形図で「3」で始まる数は全部書きだしておいたので、一番大きい数は「32.1」と分かりました。
一番大きい「32.1」と一番小さい「1.23」の差なので、32.1-1.23=30.87です。
練習問題
作成中です(2021.7.27)
循環小数の問題(受験小4)
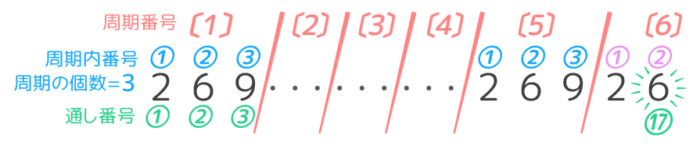
1/3を分数に直すと1÷3=0.333…と3がずっと続きます。また17を小数に直すと1÷7=0.142857142857…と「142857」という6個の数字が繰り返し並びます。
このような数を「循環小数」と呼び、連続する数字の上に点をつけて「0.3」のように表します。
→同じ数字の列が繰り返し並ぶ小数
連続する数字の上に点を付けて表す
(例)「0.3333…」→「0.3」
(例)「1.232323…」→「1.23」
(例)「0.142857142857…」→「0.142857」
循環小数の周期算
循環小数の数の並びは決まったパターンが繰り返し出てくるので「周期算」の問題になります。
(例)「2,6,9,2,6,9…」の17番目を求める
→1周期に3個の数があるので17÷3=5…2で、
5周期の後の2個目(第6周期の2番目)と分かる。
→周期の2番目なので「6」
→Nを1周期の個数(A)で割った答えがB,余りCの時、
N番目の数はB個の周期が出た後のC個目
=第(B+1)周期のC番目。
確認テストをどうぞ
1÷7を計算をした時、小数第３2位の数字は何ですか？
→( 1÷7=0.142857142857…でこれは1周期に6個の数を含む数の並びになっている。)
→( 32番目の数は、32÷6=5…2なので5周期の後の2個目、つまり6周期の2番目の数「4」と分かる。)
周期算をじっくり学びたい・解きたい人は関連記事「周期算」を見て下さい。
循環小数を分数に直す
反対に、循環小数を分数に直す問題もあります。
2-1:循環小数を分数に
(ヒント)
どこまでも続く「1」を一気に消します
(解答)
「0.1」は「0.1111…」 と「1」がどこまでも続きます。このどこまでも続く部分を消すために「0.1」を10倍した数を考えると「1.1111…」になります。
もとの数「0.1」をA,10倍した数をBとして、AとBを縦に並べてみるとこうなります。
B=1.111111111111111…
A=0.111111111111111…
ここで、B-Aをすると…
－)A=0.11111111…
B-A=1.00000000…
あの無限に続いていた「1」が1つを残して全滅！！してしまいました。ちょっと可愛そうな気もしますね…
とにかく、B-A=1 ということが分かりました！
そしてBはAを10倍したものつまり「Ax10」なので、B-A＝Ax10-A=A×9 ですね。
ということは、B-A=A×9=1 になります。
これでAが分かりますね。
A×9=1 を逆算して、A=1÷９＝19と分かりました！
気持ち良い解き方ですね…よね？興味がある人は練習して下さい
もう少し練習してみましょう
2-2:循環小数を分数に
(ヒント)
続く部分を消すには何倍すればよいか、考えましょう！
(解説)
もとの数「0.3」をA、10倍した数をBとして、B-Aをすると…
–)B=12.323232323…
–)A=11.23232323…
B-A=11. アレ？1
後ろの「232323…」が消えませんね！困りました。
試しに100倍してみましょう。もとの数「0.3」をA、100倍した数をCとして、AとCを小数点をそろえて縦に並べてみるとこうなります。
C=123.23232323…
A=121.23232323…
ここで、C-Aをすると…
–)C=123.23232323…
–)A=121.23232323…
C-A=122 消えた♪1
後ろの「232323…」が消えました。10倍では「ずらし方」が足りなかったということです。
ともかくC-A=A×100-A×1=A×99=122ということが分かりました！
A×99=122 を逆算して、A=122÷99＝12299＝12399です！！(汚い答えになってしまいました…)
確認テストをどうぞ
「0.3」を分数に直しなさい
→「0.3」をA、10倍した数をBとして、B-Aをすると…
B-A=A×9=3 と分かるので、A×9=3 を逆算して、A=3÷９＝39＝13
–)B=3.3333333…
–)A=0.3333333…
B-A=31
爽茶「大数/小数/分数/がい数のまとめ」に戻る
おしらせ
中学受験でお悩みの方へ
そうちゃ「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。