「中実方陣」を予習・復習したい中学受験生の方へ
もしかして「方陣算って難しそう」方陣算が苦手」と思っていませんか?
実は、図の書き方を一つ覚えるだけで方陣算は簡単に解けるようになるんですよ♪
この記事では東大卒講師歴20年の図解講師「そうちゃ」が「区切り図」を使った分かりやすい解き方を説明します。
記事を読んで問題を解けば「中実方陣」が得意になっているでしょう
中実方陣の石の数
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
まずは「(中実)方陣」が何か見ながら問題を解きましょう。
中実方陣は人や石がぎっしりと正方形や長方形の形に集まった形。昔の戦争で歩兵が作っていた陣形です。
方陣の大きさは、縦・横に人が何人並んでいるかで表します。
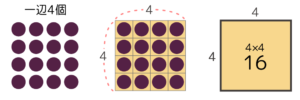
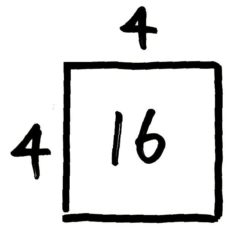
たとえば、一辺4人の中実方陣は4×4の正方形になります。
●●●●
●●●●
●●●●
この中実方陣は4×4=16の人から出来ています。
つまり、タテ・ヨコが等しい一辺A個の中実方陣に含まれる石の数は「A×A」個です(正方形の面積を出すのと同じ計算)。
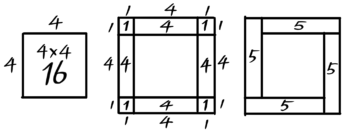
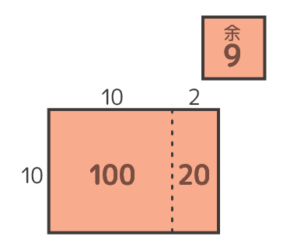
さて、問題を解く時は、「一辺が20個」のように石を実際に掛けない場合も多いです。その時は「区切り図」というのを書きます。
タテとヨコの石の数を長さのように書き、中の石の数を面積と同じ公式で出して書き込みます。
さきほどの4×4の中実方陣の場合「区切り図」はこうなります。
そのかけ算で石の数を中に書く
(ここではただの正方形の図)
中実方陣の意味は分かったので、次は中実方陣を使った問題を解いてみます。
最外周の石
一辺から最外周を求める
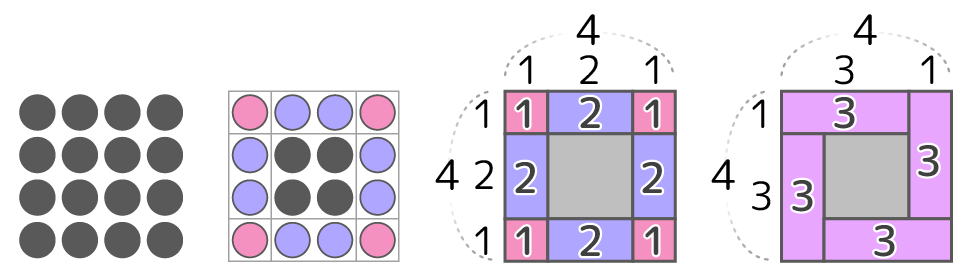
基本的でよく問われるのは、中実方陣の最外周(一番外側のひとまわり)にはいくつ石がならんでいるか?です。
これを考える時は、まず石を角(かど)の4つの石と辺の石に分けて「区切り図」にしてみます。

漢字の「井」のように区切るので「井の図」と呼んでいます。このように、四隅と辺に区切るのが方陣算の一番のコツです!
この「井の図」を見れば、最外周の石は(1×4)+(2×4)=12個と分かりますね♪
ちなみに、塾の授業やテキストでよく見かけるのは下のような図ではないでしょうか?
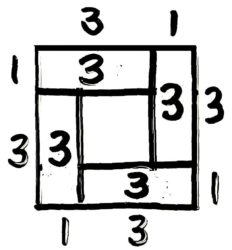
これは、角にある石とそれ以外の石を1セットずつ組み合わせた状態を区切り図にしたもので、確かに分かりやすいのですが…図が苦手な生徒の場合は、上手く書けないことがあります。
一方、先程の「井」の図は書くのが簡単で、しかも応用問題でも答えが出せるスグレモノです。
そこで、私の授業では最初に「井」の図を書き、好みでうずまき図に直すように指導しています。
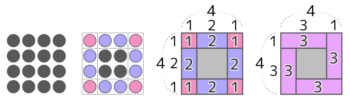
最外周を角と辺の石に分け(左から2番目の図)
区切り図(井の図)にする(左から3番目の図)
角と辺を1つづつ合体させ「渦の図」に(右端の図)
ちなみに、うずまき図を使って考えると、石を3個含む同じ形が4個できるので、最外周は3×4=12と分かります。
公式にすると、「一辺A個の中実方陣の最外周の石の数は(A-1)×4」になります。A×4ではないことに注意しましょう。
→(A-1)×4 個
(例)一辺4個の方陣の最外周の石の個数
(4-1)×4=12個
確認テストをどうぞ
一辺10個の中実方陣の最外周の石の数は?
→( (10-1)×4=36個 )
最外周から一辺を求める
反対に最外周の石の数から一辺を聞かれた場合でも、公式を使って逆算するか、区切り図を書けば解けますね
2-1:最外周から一辺
解説
公式「一辺Aの方陣の最外周は(A-1)×4」を使うと「(A-1)×4=48」です。この逆算を解きます
(A-1)=48÷4=12 → A=12+1=13 つまり一辺は13個と分かります。
別解
区切り図(井の図)を書いても良いでしょう。

○×4=48-4=44 → ○=44÷4=11 なので、一辺?は11+1+1=13と分かります。
もっと問題を解きたい人は「オススメ教材」を見て下さい
もう一周増やす
一辺A個の中実方陣の「外側にもう『一周』増やす」場合は{(A+1)×4}個の石が必要になる。これは公式として覚えるというよりは下の図をイメージして式を作ることができればOKです。
一辺4個から一周増やすと
❶❷❸❶ → ❶●●●●❷
❸●●❷ → ❷●●●●❸
❷●●❸ → ❸●●●●❹
❶❸❷❶ → ❹●●●●❺
❶❸❷❶ → ❺❺❹❸❷❶
区切り図で考えると、こうなります
列を増やす/減らす
次は「列を増やしたり減らしたり」する問題を考えます。
タテヨコを一列増やす
中実方陣の「列を増やす」というのは、一辺の長さを1個増やすことです。
たとえば一辺4個の中実方陣のタテヨコ一列ずつ増やすと下のようになります。
タテヨコ一列増やすと
一辺5個の中実方陣になる
●●●● → ●●●●❶
●●●● → ●●●●❷
●●●● → ●●●●❸
●●●● → ●●●●❹
四隅●が1個増えるので、
(4×2)+1=9個増える
つまり一辺A個の中実方陣のタテヨコ一列を増やすには石が(A×2)+1 個必要です。
区切り図を書くとこうなります。応用問題ではこの図が書けないと解くのが難しくなるので、よく練習して下さい
一列増やす場合の「区切り図」
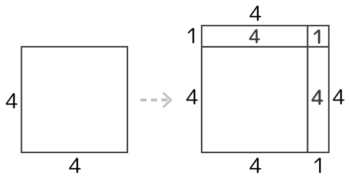
1×1=1の区切りが1つあるので
合わせて4×2+1=9個必要と分かる
もう一つの考え方
こんな風に考えてもよいでしょう。
一辺4の中実方陣の石の数は4×4=16個、一列増やした一辺5の中実方陣の石の数は5×5=25個、25-16=9個
つまり、一辺Aの方陣のタテヨコ一列を増やすのに必要な石の個数は「(A+1)×(A+1)-A×A」という公式にもなります。
頭の片隅に入れておくと、中空方陣の問題を解く時に役立ちます。
一辺7個の中実方陣をタテヨコ一列ずつ増やすのに石が何個必要か?
→( (7×2)+1=15個 または 8×8-7×7=64-49=15 )
余った石で一列増やそうとするが足りない…
石が14個あったとしましょう。この石で一辺3個の方陣を作ると、14-(3×3)=5個の石●●●●●が余っています。
●●● ●●●●●
●●● ●●●●●
この余った石を方陣の回りに並べても、一辺4の方陣には出来ません…
●●●●
●●●
●●●
一辺3の方陣のタテヨコ一列を増やすには、上の公式より3×2+1=7個の石が必要なので、あと2個●●あれば一辺4の方陣が作れます。
●●●●
●●●●
●●●●
今の状況を区切り図にするとこうなります。
余りを並べるが足りない
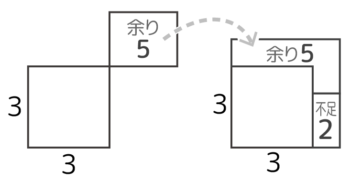
この考え方・図の書き方を使って、問題を解いてみましょう。クイズだと思って気楽にチャレンジ♪
3-0:余ったが足りない
碁石は何個ありますか?
ヒント
結局一列増やすのに何個必要なのか、を考える
解説
正方形につめて並べる=中実方陣です(一辺は分かりません…)。余った9個をテキトーに合わせて書くとこうなります。
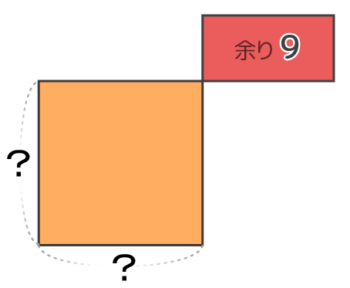
余った9個でもう一列増やそうとしたら2個足りなかった、という事は11個必要だったということです。
2個足りない
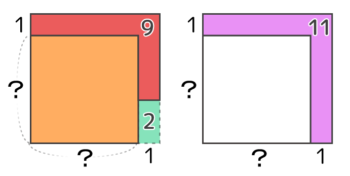
9+2=11個必要だと分かる
これを区切り図にすると…もとは一辺5個の方陣だったと分かります。
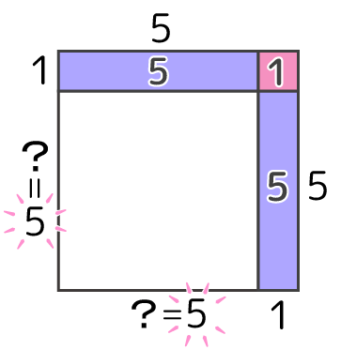
?=5だと分かる
これで石の数は方陣部分が5×5=25個で余りが9個だったので、合計は25+9=34個だったと分かります。
もっと問題を解きたい人は「オススメ教材」をご覧ください
長方形の中実方陣
ここまで方陣は正方形でしたが、長方形の方陣もあります。
少し面倒くさくなりますが、根本的な考え方は同じです。
石の数
タテA個ヨコB個の中実方陣に含まれる石の数は「A×B」個です。長方形の面積の公式と同じです
実体図と区切り図
●●●●
●●●●
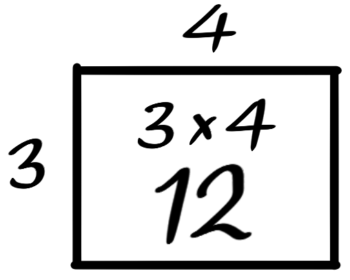
3×4=12個の石が含まれる
タテ8個ヨコ14個の中実方陣に含まれる石の数は?
→( 8×14=112個 )
最外周の石
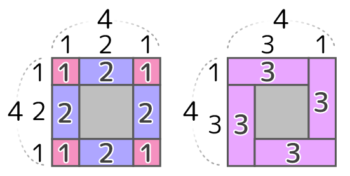
縦3個横4個の方陣の最外周の石の数を出してみましょう
正方形の場合と同じように、まず角の石とそれ以外に分けた「井の図」を書きます。これでも答えは出せますが…
実体(左)と「井の図」
●●●●
●●●●
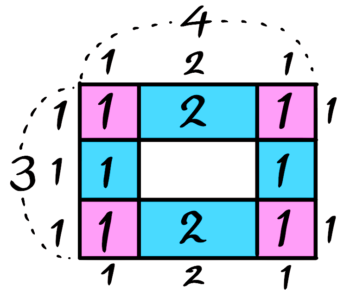
さらに「うずまき図」にもしてみましょう。
実体(左)と「うずまき図」
❷●●❷
❶❷❸❶
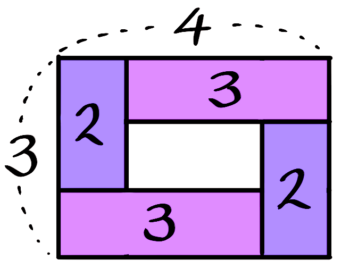
二つずつできるので最外周の石は
(3-1)×2+(4-1)×2=10個
これを観察すると、長方形の最外周に(3-1)=2個と(4-1)=3個の区切りが二つずつできるので最外周の石は(3-1)×2+(4-1)×2=10個です。
公式にすると、縦A横Bの長方形の方陣の最外周の石の数は「(A-1)×2+(B-1)×2」になります。
4-2:長方陣の最外周の石
ヒント
四隅を区切って「(井の図)」を描く
解説
区切り図を書くとこうなります。
最外周の石の区切り図
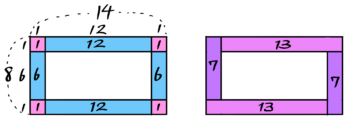
「井の図」だけでも解けますが、ここでは参考のために「渦の図」も描いてあります。
「井の図」からは、12×2+6×2+1×4=40個、「渦の図」からは7×2+13×2=40個 と求められます
一列ずつ増やす
長方形の方陣をタテヨコ一列ずつ増やす場合を図にするとこうなります。
長方形の増幅と区切り図
●●●●
●●●●
●●●●❶
●●●●❷
●●●●❸
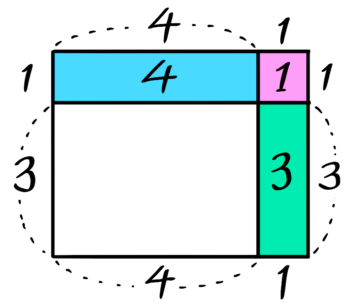
3+4+1=8個増える
この場合も、角の石に注目すると分かりやすいですね。公式にすると「タテAヨコBの長方形の方陣を一列増やすのには石が A+B+1個必要」です。
5-1:長方陣をタテヨコ一列ずつ増やす
ヒント
区切り図(井の図)!
解説
一列増やした状態の区切り図(井の図)を書くとこうなります。
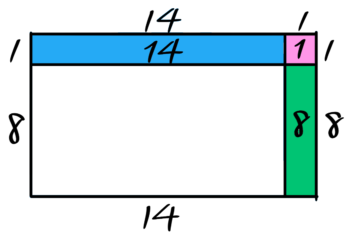
これを見れば、必要な石の数は14+8+1=23個と分かります。
拘束式の長方陣
最後は「ヨコの数がタテより2個多い」「タテがヨコの2倍」のように、タテヨコのうち一方がもう一方の大きさに拘束される場合です。
区切り絵(井の図)を最大限に活用して、平面図形の問題のように解きます。
最外周から石の合計を出す
差タイプ
6-1:拘束型長方陣の最外周(差タイプ)
解説
まず「ヨコの数がタテより2個多い中実方陣」はこうなります。
つぎに最外周の区切り図と最外周の数を並べて…
最外周の個数を並べる
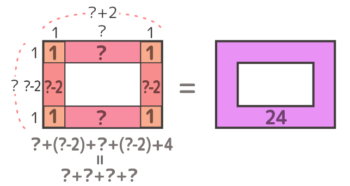
?=6 と求められる
比べると?+(?-2)+?+(?-2)+4=?+?+?+?=24と分かります。
この逆算を解くと ?=6です。
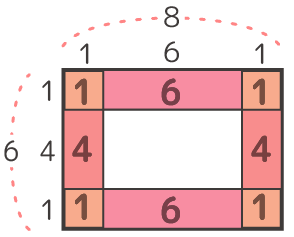
中実方陣のタテが6ヨコが8と分かったので、石の数は全部で6×8=48個です。
比タイプ
6-2:拘束型長方陣の最外周(比タイプ)
解説
タテの長さを?とおいて区切り図を書きます。
これを区切り図にして、最外周の石の個数と並べると、(?×8)-4=68 と分かります。

この逆算を解くと、(?×8)=68+4=72 ?=72÷8=9 と求められます。
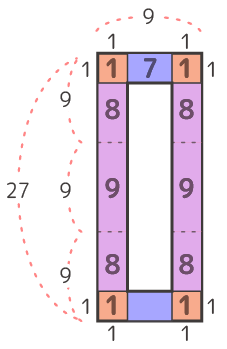
石の合計は27×9=243個
これでタテ27ヨコ9なので、石の合計は27×9=243個と分かりました。
タテヨコ一列ずつ増やす
上で解いた問題の長方陣バージョンです。
例えば「ヨコの数がタテの数より2個多い長方形の中実方陣を作ったら石が9個余ったので、タテヨコを一列づつ増やそうとしたら石が14個不足した」という場合。
まず「ヨコの数がタテの数より2個多い長方形の中実方陣を作ったら石が9個余った」のを図にするとこうなります(図A)。
この後は外に増やすので、さっきと違って「2」で中を区切っています。
を作ったら石が9個余った(図A)
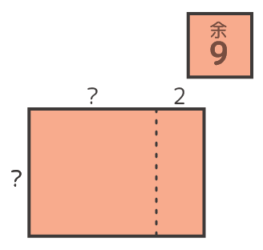
次に「タテヨコを一列づつ増やそうとした」計画の図はこうなります(B)
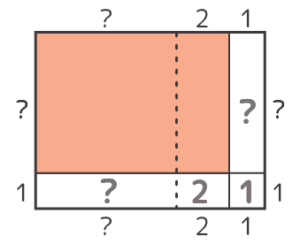
増える「L字」部分に、分かるだけの
長さと面積(石の数)を書く
同じ「?」の面積の部分が2個できます。また右下隅の「1」は見慣れていますが、その隣に「2」が出来るのが今までにない特徴ですね。
そして「余った9個とあと14個必要だった」図はこうなるので、
図BのL字に流し込む
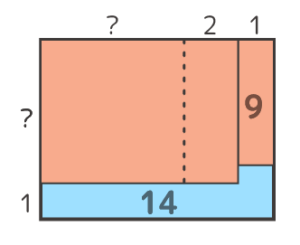
9と14の境目はテキトーに書いてもよい。
一列ずつ増やすのに23個必要だったと分かります(図C)
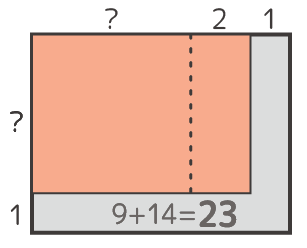
B図とC図を比べると、面積の「?」が{23-(2+1)}÷2=10と分かります(図D)


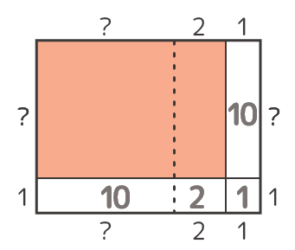
これで長さの「?」も10÷1=10と分かります。これを最初の図Aに書くと石の数が{10×(10+2)}+9=129個と分かります。
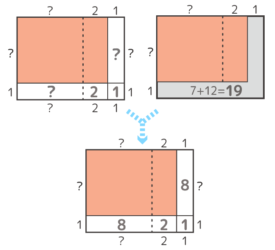
ヨコの数がタテの数より2個多い長方形の中実方陣を作ったら石が7個余ったので、タテヨコを一列づつ増やそうとしたら石が12個不足した。石の数は?
→区切り絵に分かる個数(面積)を書くと、面積の「?」が( {19-(2+1)}÷2=8 )、長さの「?」は( 8÷1=8 )と分かる。
→石の数は( {8×(8+2)}+7=87個 )
確認テストとお礼
空欄をタッチする(スマホ)かマウスポインタをのせる(パソコン)と答えが表示されます。
- 中実方陣の石の数=( タテ×ヨコ )
- 一辺A個の中実方陣の最外周の石の数
=( (A-1)×4 ) - 一辺A個の中実方陣をタテヨコ一列増やすのに必要な石の数
=( (A×2)+1 ) - 一辺A個の中実方陣の最外周をもう一週増やすのに必要な石の数
=( (A+1)×4 )←覚えずともOK
オススメ教材
 爽茶
爽茶もっと問題を解きたい人にオススメの教材
「分かりやすい!」と評判の
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ