「石を三角形に並べる問題が苦手…」という中学受験生の方へ。
ルールがあったのは覚えているけど、ハッキリ思い出せないのでしょうね。
この機会にルールをきちんと憶えてしまいましょう！
この記事は、石を三角形に並べた「ピラミッド算」の考え方解き方を、東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく解説します。
記事を読んで真似すれば、もう苦手では無くなっているはずですよ！
三角形に石を積む
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
今回は石を三角形に並べます。丸太を積んでいるのを正面から見て、木の断面の年輪が見えているような？イメージです。三角形=ピラミッド
組体操で作るピラミッドのように石を三角形に積んでいきます。
石の段が積み上がっていくイメージ
→
→
→
(一番下の石)
(石の合計)
●
●
●
1個
1個
●
●
●●
2個
1+2=3個
●
●●
●●●
3個
1+2+3=6個
最下段の石の数
一番下の段の石の数は段数と同じになっているので、N段のピラミッドの最下段の石の数はN個です。
15段のピラミッドの最下段の石は何個？
→( 15個 )
石の合計
全部の合計
求め方
上で見たように、1、(1+2=)3、(1+2+3=)6…と増えていきます(この数を三角数という)が、これを計算で求めます。
N段のピラミッドの石の合計は、1+2+3+…N 個になり、これは等差数列の和と同じ考え方で、N×(N+1)÷2と計算できます。
●●
●●●
●●●●
→
●●
●●●
●●●●
●●○○○
●●●○○
●●●●○
同じものをもう一つ付けると
4×5の長方形になる。
4×5の長方形の半分なので、
4×5÷2 で求められる。
等差数列の合計＝(はじめの数+N番目の数)×N÷2 で、N団のピラミッドは「はじめの数」＝1、「N番目の数」=N なので、(1+N)×N÷2 になります。ここでは覚えやすいようにN段のピラミッドの石の合計は N×(N+1)÷2 としておきます。
よく分からない人は「等差数列の和」を見て下さい。
→(1+2+3+…+N)個なので
等差数列の和の公式で(1+N)×N÷2
●図で考えて、N×(N+1)÷2 でも良い
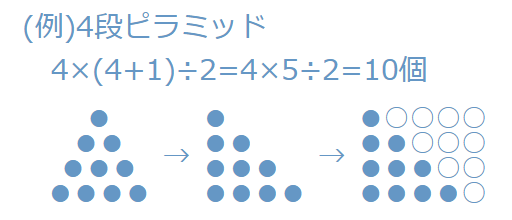
(例)4段ピラミッド
4×(4+1)÷2=4×5÷2=10個
●●
●●●
●●●●
→
●●
●●●
●●●●
●●○○○
●●●○○
●●●●○
15段ピラミッドの石の合計は？
→( 15×(15+1)÷2＝120個 )
合計から段を求める
上と逆に、石の合計から段数を求めてみます。
実はこの問題は計算だけでは完璧には解けません。試行錯誤が必要になります。
1-1:ピラミッドの石の数から段数を求める
解説
ピラミッドがN段だとすると、1+2+…+N=(N+1)×N÷2=120になります。
(N+1)×N÷2=120から、(N+1)×N=240と分かります。
そして「(N+1)×N」は連続する2つの整数をかけたものなので、
「かけ合わせたら240になるような連続する2つの整数」を見つければ良いと分かります。
2ケタの数の平方数(11×11=121,12×12=144…19×19=361)を覚えていれば(→参考記事)、240に近い「15×15=225」を思い出して、240は225より大きいので「15×16が良さそうだな」と考えて、実際に15×16を筆算してみると240になりました♪
一方、2ケタの数の平方数を覚えていない場合でも「10×10=100」「20×20=400」で「240は100と400の間」というのは分かるので、10と20の間の15で「(N+1)×N」を作って試します。この場合は「15×16」を試します。
すると(偶然ですが)240になりました♪(もし筆算の結果が240より小さければ、今度は16×17を…大きければ14×15を…と240になるまで調べていきます。)
これでN=15、つまりピラミッドは15段と分かりました。
確認テストをどうぞ
三角形に石を詰めて並べたら276個だった。何段並べたか？
→( N段の合計N×(N+1)÷2=276なのでN×(N+1)=276×2=552になるようなNを探す )
→( 20×20=400、30×30=900、552はその間にあるので、まずは25×26を試してみると25×26=650で大きすぎるので、数を小さくしていく )
→( 24×25=600でまだ大きい。23×24=552で一致♪ )
→( N=23なので、23段 )
一段おきの合計
一段おきに(奇数段だけ)石を足していくと「平方数(四角数)」になります。
一段おきの石の合計は平方数になる
●
●
1段
1個
(1×1)
●
●●
●●●
3段
1+3=
4個
(2×2)
●●
●●●
●●●●
●●●●●
5段
1+3+5=
9個
(3×3)
●●
●●●
●●●●
●●●●●
●●●●●●
●●●●●●●
7段
1+3+5+7=
16個
(4×4)
たとえば5段ピラミッドの奇数段(1段と3段)の石●と偶数段の石●の合計を出します。
「5」は奇数としては「(5+1)÷2=3」番目なので、5段ピラミッドの奇数段の石●の数は「3」の平方数3×3=9個になります。そして偶数段の石●は全部の合計(5×6÷2=)15個から●9個を引いた数なので6個と分かります。
一応、公式にすると、Nが奇数の時、N段ピラミッドは奇数としては「(N+1)÷2」番目のピラミッドになっているので、N段ピラミッドの奇数段の合計は{(N+1)÷2}×{(N+1)÷2} 個 になりますが、おぼえるというよりも問題が解ければいいですよ。
奇数段は黒い石、偶数段は白い石で15段のピラミッドを作る時、黒い石は何個か？
→( 15段ピラミッドは奇数では(15+1)÷2=8番目のピラミッドなので、その奇数段(黒い石)の合計は8×8=64個 )
さっきの15段ピラミッドの白い石の個数は？
→( 15段ピラミッドの全部の石の合計は15×(15+1)÷2＝120個で、黒い石が64個あるから、白い石は120－64＝56個 )
奇数個だけのピラミッド
上の問題の「奇数個」だけのピラミッドも入試に出てきます。
一段おきの石の合計は平方数になる
●
●
1段
1個
(1×1)
●
●●●
2段
1+3=
4個
(2×2)
●●●
●●●●●
3段
1+3+5=
9個
(3×3)
●●●
●●●●●
●●●●●●●
4段
1+3+5+7=
16個
(4×4)
こちらは単純に「段数x段数」で石の合計を求めることができますね。
また、最下段の石の数は段数=Nとすると「N番目の奇数」で「Nx2-1」になります。例えば3段目は3番目の奇数なので3x2-1=5個になっているのが分かります。
1段目は1個、2段目は3個、3段目は5個、というように奇数個の石で8段のピラミッドを作る時、石は全部で何個か？
→( 8×8=64個 )
最下段の石が19個になっているピラミッドの石の数の合計は？
→( このピラミッドをN段とする、Nx2-1=19の逆算を解いて□=10(このピラミッドは10段)。よって石の合計は10×10＝100個 )
最外周の石の数
ピラミッドの一番外に並んでいる石の数を答える問題
これは方陣と同じような「区切り」を考えれば良いですね。
●●
●●●
●●●●
●●●●●
→
●●
●●●
●●●●
●●●●●
●●
●●●
●●●●
●●●●●
一つづつ組み合わせると
5-1=4個の石を含む「区切り」が3つできるので、
最外周の石は4×3=12
N段のピラミッドの最外周の石は (N-1)×3 と分かります。
15段ピラミッドの最外周の石の個数は？
→( (15-1)×3=42個 )
まとめの確認テスト
- N段ピラミッドの最底辺の石の個数=( N個 )
- N段ピラミッドの石の合計
＝( N×(N+1)÷2 個 ) - N段ピラミッド(Nは奇数)の奇数段だけの石の合計
→Nは{(N+1)÷2}＝M番目の奇数で
＝( M×M 個 ) - N段のピラミッドの最外周の石の個数
=( (N-1)×3 個 ) - N段のピラミッドの最外周をもう一周増やすのに必要な石の数
=( (N+2)×3 個 )
オススメ教材
爽茶●方陣算だけを解きたい場合は「方陣算(基本)(応用)」(サイパー算数)
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題」シリーズ(日能研)
●小6受験生には「算数ベストチェック」(日能研)
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評！
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!