「中空方陣に苦手意識がある…」という中学受験生の方へ
確かに「中空方陣」は考えていると頭がゴチャゴチャしてきますよね…でも大丈夫!
たった一つの図を書くだけで「全然わからない」から脱出できますよ!
東大卒講師歴20年の図解講師「そうちゃ」が方陣算を分かりやすくする「区切り図」を使って中空方陣の基礎から説明します。
記事を読んで例題を解けば、中空方陣が得意になっているでしょう♪
(復習)中実方陣
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
中「空」方陣は中「実」方陣の続きなので、中実方陣の基本を軽く復習。「分かるよ」という人はジャンプして下さい。
中実方陣は正方形(または長方形)にぎっしり石を並べた形で、全体の石の数の求め方は正方形(長方形)の面積と同じでした。
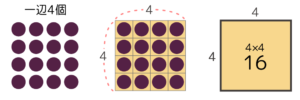
そのかけ算で石の数を中に書く
最も外側の一周(最外周)の石の数の出し方は中空方陣でも使うので大切です
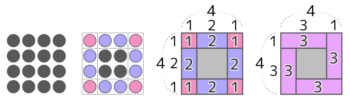
最外周を角と辺の石に分け(左から2番目の図)
区切り図(井の図)にする(左から3番目の図)
角と辺を1つづつ合体させ「渦の図」に(右端の図)
この「区切り図」特に「井の図」(左から3番目)が方陣算を得意にするためのコツです。
詳しく読みたい問題を解きたい人は「中実方陣」を読んで下さい
中空方陣の石の数
中空方陣は人や石が内側を空けて正方形や長方形の形に集まった形(戦場でケガ人を中に入れて守ったりする陣形です)
中実方陣との違いを見て下さい。
中実方陣
●●●●●●
●●●●●●
●●●●●●
●●●●●●
●●●●●●
ぎっしり
の中空方陣
●●●●●●
●●●●●●
●●●●●●
●●●●●●
●●●●●●
がある
の中空方陣
●●●●●●
●●●●●●
●●●●●●
●●●●●●
●●●●●●
なっている
はじめに中空方陣の石の数の計算方法を求めます
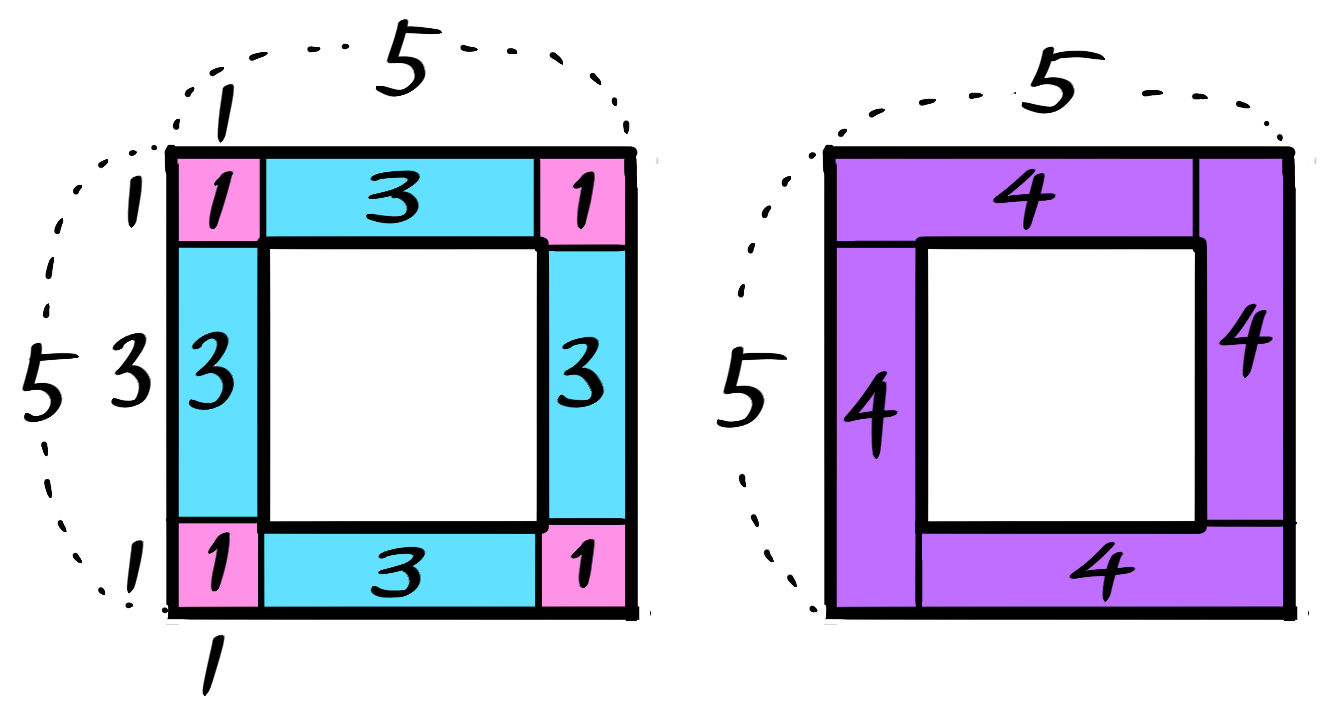
一列の中空方陣
1列の中空方陣の石の数は、中実方陣の最外周の石の数と同じ方法で求めます。
例えば一辺5個で一列の中空方陣(左の図)の場合、角(カド)にある石4つとそれ以外を「井」のように区切ると、角(ピンク)と辺(ブルー)に分けられます(中央の図)。これを合計すれば石の数が (3×4)+(1×4)=16 と分かります。
●●●●●
●●●●●
●●●●●
●●●●●
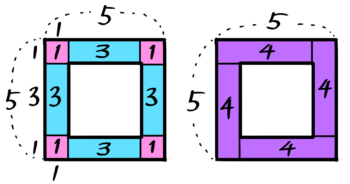
中空方陣の石は全部で(5-1)×4=16個
また、ピンクとブルーの区切りを一つづつ合体させると、石を4つ含む同じ形が4つできます(右の図)。これを合計して4×4=16 と求めることも出来ます。
このサイトでは、中央の図を「井の図」、右の図を「うずまき図」と呼びます。(「井の図」の方が基本的で大切です)
うずまき図での計算を公式にすると、一辺Aで一列の中空方陣の石の数は「(A-1)×4」個です。
中空方陣の石の数
→(A-1)×4 個
*一辺Aの中実方陣の最外周の個数と同じ。
もうひとつの考え方
一辺がA個で一列の中空方陣では、中の空洞の一辺は(A-2)個になっている。
したがって、石の数はA×A-(A-2)×(A-2)と表すこともできる。
頭の片隅に入れておきましょう。
確認テストをどうぞ
一辺10個1列の中空方陣の石の数は?
→( (10-1)×4=9×4=36個 )
2列の中空方陣
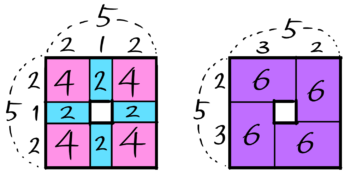
2列の中空方陣では「井の図」を作ると角に 2×2=4個の石ができます。辺の石も2列になっています。
いきなり「うずまき図」をかいているが
まず「井の図」を書くことが大事
そして「角」と「辺」を一組ずつ合わせると、同じ形が4つできて「うずまき図 」になります。
このとき、一つの区切りは2×(A-2)の長方形になるので、石の数は{2×(A-2)}×4 個になります
例えば「一辺5個2列」の場合、2×(5-2)×4=24個になります
(まず「井の図」を書くのがオススメ)
❸❹❷●●
●●●●●
●●●●●
●●●●●
石は全部で6×4=24個
中空方陣の石の数
→{2×(A-2)}×4 個になる
確認テストをどうぞ
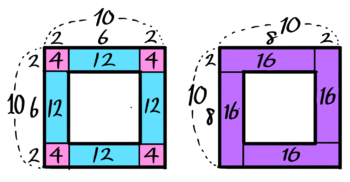
一辺10個2列の中空方陣の石の数は?
→( 2×(10-2)の区切りが4つできるので )
→( 2×(10-2)×4=64個 )
3列以上の中空方陣
1列の中空方陣の石の個数を(A-1)×4 としましたが、実は区切りが1×(A-1)の長方形なので、{1×(A-1)}×4 です。そうすると
1列の中空方陣…{1×(A-1)}×4
2列の中空方陣…{2×(A-2)}×4
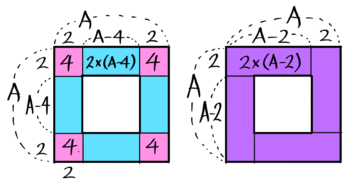
なので、3列の中空方陣の石は{3×(A-3)}×4 個、4列なら{4×(A-4)}×4 個…と予想できますね。実際それでOKです。
- 一辺A個1列の中空方陣の石の数
=( (A-1)×4 )個 - 一辺A個2列の中空方陣の石の数
=( {2×(A-2)}×4 )個 - 一辺A個3列の中空方陣の石の数
=( {3×(A-3)}×4 )個
確認テストをどうぞ
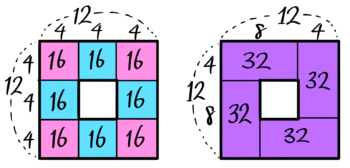
一辺が12個で4列の中空方陣に石は何個あるか?
→一辺12個4列の中空方陣の石は({4×(12-4)}×4 )個
→計算して( 32×4=128個 )
中空方陣の形を求める
今までは中空方陣の形(一辺の数と列幅)から石の数を求めましたが、今度は反対に石の数から中空方陣の形(一辺の数と列幅)を求めます。
列数と石の合計→一辺
列数が分かる場合は角の様子が分かるので、それを手がかりにします。
2-1:中空方陣(一辺を求める)
解説
区切り図(井の図)を書くと、角の石は1つの区切りが3×3=9個で合計9×4=36個と分かる
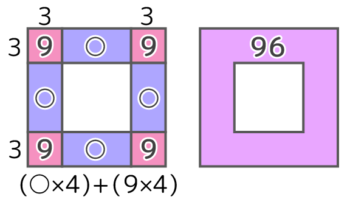
辺の石の合計は96-36=60個なので、辺の石1つの区切り(○個)は60÷4=15で、これは短い辺が3の長方形なので長い辺は15÷3=5と分かる。。
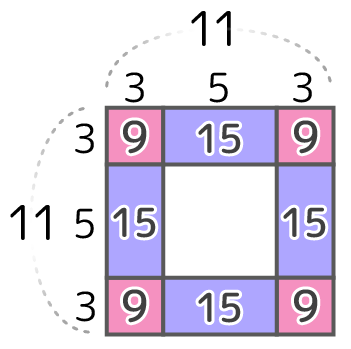
あとは簡単
これで一辺の長さは3+5+3=11と求められる。
一辺と石の合計→列数
一辺が分かる場合は中実方陣とした場合の個数がわかるので、実際の石との差が中の空洞になります。
つまり、一辺A個で空洞の一辺がB個の中空方陣の石の数=(A×A)-(B×B) 個 です。
この式を使って問題を解きます。
2-2:中空方陣(列数を求める)
解説
一辺12個なので、中実方陣だとすると12×12=144個になる。
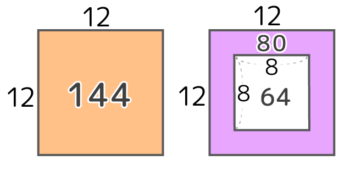
64=8×8より、一辺8
実際の個数80個との差144-80=64個が中の空洞になり、64=8×8なので、空洞の一辺が8と分かる。
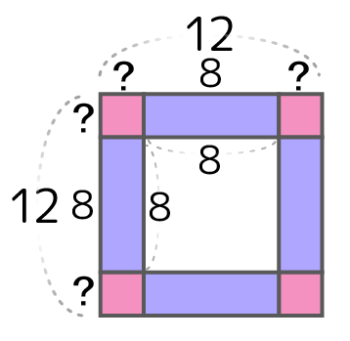
区切り図を見て考えると列数は(11-8)÷2=2列と求められる。
長方形の中空方陣
石の個数
区切り図を書けば分かるでしょう。
例えば「タテ12個ヨコ10個,3列の中空方陣」の石の個数を出してみましょう。
の中空方陣

今まで同様、角の石と辺の石のグループに分けた「井の図」を書きます
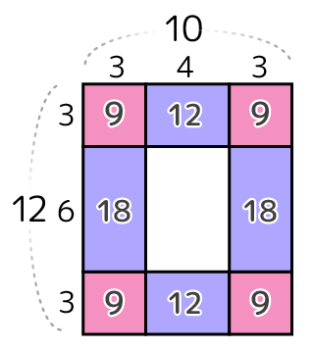
これで石の合計は(9×4)+(12×2)+(18×2)=96個と出せますが、区切り同士を合体させてみます。
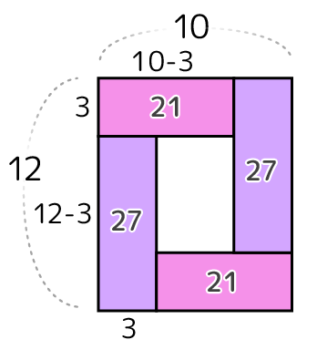
長方形では「渦の図」は2種類の区切りから出来ています。
この図を使うと、石の数は{3x(12-3)}x2+{3x(10-3)}x2=96になります
公式化すると、こんな感じでしょう。
●タテA個ヨコB個,N列の中空方陣の石の数
={N×(A-N)}x2+{N×(B -N)}x2
(例)タテ12個ヨコ10個,3列の中空方陣の石の数
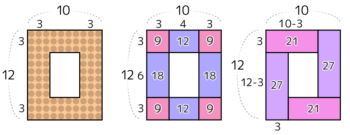
{3x(12-3)}x2+{3x(10-3)}x2=27×2+21×2=96
もう一つの考え方
中実方陣とした場合から中央の空洞を除く考え方だと、12×10-(12-3×2)x(10-3×2)=120-24=96 と計算出来ますね。
以上の考え方で例題を解いてみましょう
3-1:中空長方陣(石の合計を求める)
解説
区切り図(井の図)を書いて、面積を出すように石の数を書き込みます。
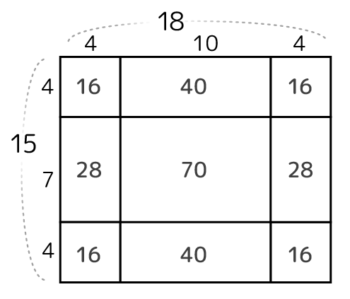
ここからは、自分の好きな計算方法で行きましょう。
「井の図」のまま 16×4+40×2+28×2 、「渦の図」にして (16+28+16+40)x2 、「空洞を引く」考え方で 15×18-10×7
いずれにしろ、答えは200個になります。
拘束型の中空長方陣
タテヨコどちらか一方がもう一方との関係で拘束される場合です。
「差タイプ」と「比タイプ」があります。
まとめ確認テスト
空欄をタッチする(スマホ)かマウスポインタをのせる(パソコン)と答えが表示されます。
- 一辺A個1列の中空方陣の石の数
=( (A-1)×4 )個 - 一辺A個2列の中空方陣の石の数
=( {2×(A-2)}×4 )個 - 一辺A個3列の中空方陣の石の数
=( {3×(A-3)}×4 )個 - 一辺A個で空洞の一辺がB個の中空方陣の石の数
=( (A×A)-(B×B) )個
オススメ教材
 爽茶
爽茶もっと問題を解きたい人にオススメの教材
「分かりやすい!」と評判の
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ