中学受験】石を多角形に並べた問題の解き方。たった2つのコツで簡単♪【方陣算類似

中学受験生で石を並べる問題に自信がない方へ。たしかに石がゴチャゴチャ並んでワケが分からなくなることがありますね…

でも大丈夫ですよ！たった2つの見方を身につけるだけで難しさは無くなります。

この記事は東大卒講師歴20年の図解講師「そうちゃ」が石を五角形・六角形などに並べる場合の問題の考え方をわかりやすく説明します。

記事を読んで真似すれば、頭がスッキリ整理されて問題も落ち着いて解けるようになるでしょう。

「多角形並べ」の特徴

爽茶そうちゃ

方陣算では四角形に、ピラミッド算は三角形に石をならべました。今回は五角形・六角形などに石を並べます。

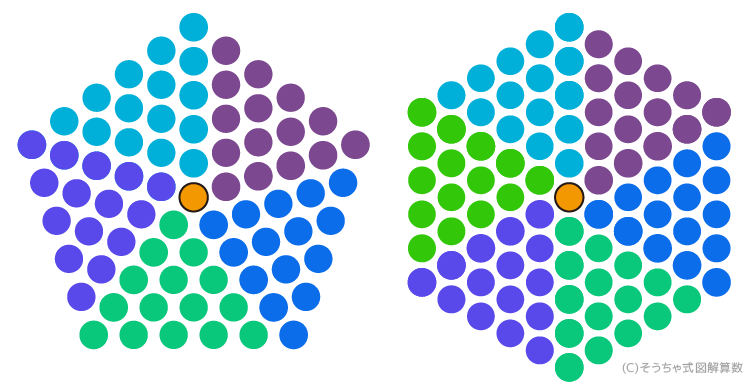
石を五角形・六角形など多角形の形に並べると下のようになります。

左から一辺6個の四角形・五角形・六角形

左端の「四角形」を見て「方陣算」を思い出す人もいるでしょう。しかし実は、この並べ方は方陣算とは違うのです。

どこが違うか分かりますか？

中心に○○がある

実は、この「多角形並べ」は中心に必ず1個の石(へそ)があります。

多角形並べは必ず中心に石(へそ)がある

一方、「方陣」や「ピラミッド」には中心が無いこともあります。

一辺6の方陣(左)と四角形並べ(右)方陣には中心(へそ)が無いのに対して
四角形並べの方はへそを中心に
四角形が広がっていくのが分かる

この「へそ石」をよく覚えておきましょう。

多角形並べの問題

全部の石の数

全部の石の数を答える問題です。

もとの図のままだと何個あるのか数えるのが難しいので、中心となる石(へそ)以外の石をピラミッドに分解します。

このピラミッドは多角形の辺の長さよりも1個少ない段になります。

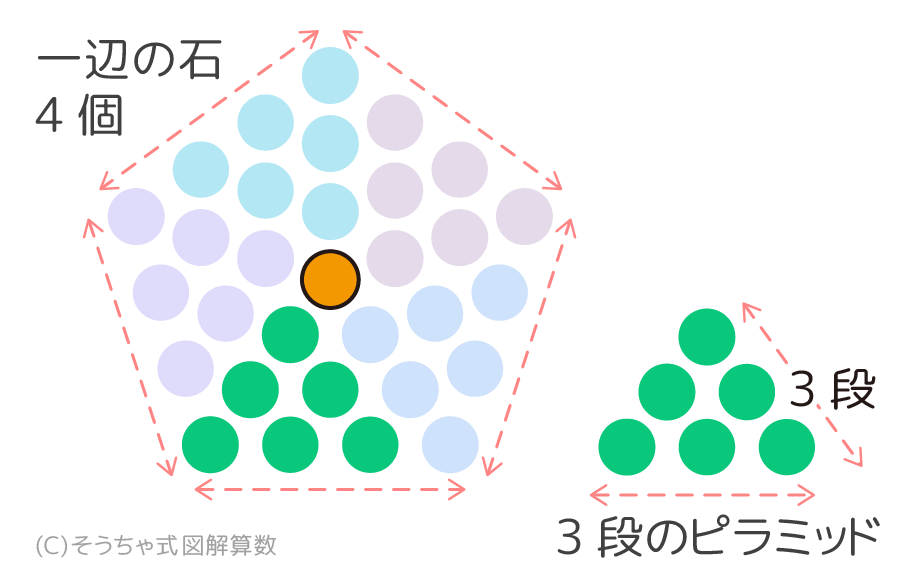一辺4個の五角形並べは…4－1=3段の「ピラミッド」が5個と
「へそ石」に分割できる。

上の図のような一辺4個の五角形の場合、ピラミッドは4-1＝3段になります。

N段のピラミッドの石の数は「N×(N+1)÷2」でしたから、3段のピラミッドには3×(3+1)÷2=6個の石があって、これが5セット30個あります。

さらに中心の「へそ」1個を加えた31個が石の合計になります。

まとめると、一辺A個のN角形並べの石の合計は [{(A-1)×A÷2}×N]+1 になります。(この公式は覚えるというよりも作ることができればOKです。)

最外周の石の数

これは方陣と同じように「最外周の区切り絵」を書くと分かります。

((方陣、五角形並べ、六角形並べの「実体図」と「区切り絵」))

一辺6の五角形の場合は最外周に5個の石を含む区切りが5個できるので(6－1)×5=25個、一辺6の六角形の場合は最外周に5個の石を含む区切りが6個できるので(6－1)×6=30個になります。

つまり、一辺がA個のN角形並べでは、最外周には(A-1)個の石を含む区切りがN個できるので、最外周の石の数は (A-1)×N個 になります。

まとめ

オススメ教材

爽茶そうちゃ

もっと問題を解きたい人にオススメ教材を紹介

参考書・問題集
●方陣算だけを解きたい場合は「方陣算(基本)(応用)」(サイパー算数)が定評あり
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題」シリーズ(日能研)がオススメ(→教材の目次・比較ページ)
●小6受験生には「算数ベストチェック」(日能研)が薄くて良いですが、詳しい説明が欲しい人には「中学入試 塾技100(算数)」がオススメ(→教材の比較ページ)

動画で学習したい人へ
「分かりやすい！」と評判のスタディサプリなら有名講師「繁田 和貴」氏による中学受験用の方陣算の動画もありますよ(小4応用の第12講)♪
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？

歴史の点数を上げたい受験生と保護者の方へ

年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ

2023年度生徒さん募集

2023年度の生徒さんの募集を開始しました(対面授業の一次募集)

東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。

詳しくはコチラのページを御覧下さい

新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから

中学受験でお悩みの方へ

そうちゃ

いつもお子様のためにがんばっていただき、本当にお疲れさまです

受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など

様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。

自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…

そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。

最後まで読んでいただきありがとうございました♪
この記事があなたの役に立てたなら嬉しいです!