わり算の答えが概数として示される数の
範囲と最小・最大を求める問題
(例:9で割った答えを小数第一位で四捨五入すると
7になる数Nの最小最大を求める)
わり算の答えの範囲を求めて
範囲の下限と上限を倍する!
「概数の応用問題を解きたい」という中学受験生と保護者の方へ。おまたせしました!東大卒講師歴20年の管理人が、中学入試でそのまま出題されることもある「かけ算わり算からの概数の復元」問題を分かりやすく図解します。
記事の最後ではプリントもダウンロードできます。ご利用下さい。
四捨五入(復習)
四捨五入の復習としてまとめを示します。
●まず目盛りの細かさ(10刻み,100刻みなど)を決める
❶2つの目盛りの真ん中より下にある数→切り捨て
❷2つの目盛りの真ん中より上にある数→切り上げ
❸2つの目盛りのちょうど真ん中の数→切り上げ
(例:175を一の位で四捨五入する場合)
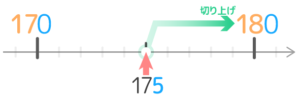
目盛りの細かさは「10刻み」で
175は2つの目盛り170と180の間にある。
ちょうど真ん中なので切り上げて180になる。
概数の応用問題
割り算(除算)からの復元
◆問題の概要
[su_spoiler title=”説明をとばす” open=”yes” style=”fancy” icon=”chevron-circle” class=”std no-trn pale dtd”]
割り算をして割り切れない場合に、四捨五入して答えにすることがあります。例えば、15÷4=3.75 なので、小数第一位を四捨五入して「4」とするような場合です。
この場合、割られる数を変えても小数第一位を四捨五入すると「4」になる計算があります。例えば「17÷4」も17÷4=4.25 で小数第一位を四捨五入すると「4」になるし、「14÷4」も14÷4=3.5 で小数第一位を四捨五入すると「4」になります。
ただ、限界があって「13÷4」になると13÷4=3.25 で小数第一位を四捨五入すると「3」になってしまいます。
このように、割り算の答えが四捨五入されている場合、割られる数はある範囲に渡って何通りか存在します。
[/su_spoiler]
前置きが長くなりましたが、このように割られるもとの数の範囲を求める(割られる数の復元)のがここでの問題となります。
例題でやり方を理解して下さい。
やり方を理解♪
例題1
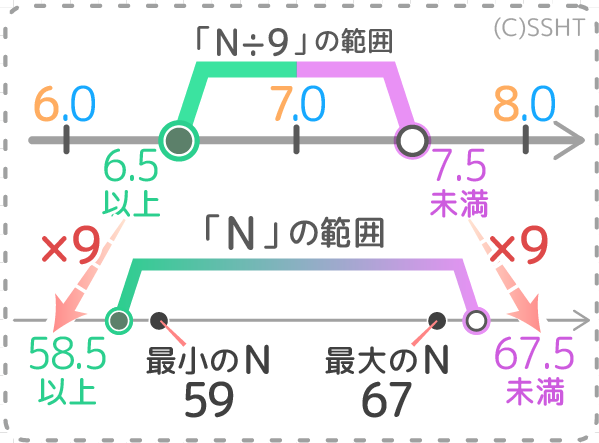
(1)「N÷9」の範囲を求めよ
(2)Nの範囲を求めよ
(3)整数Nの最小の値と最大の値を求めよ
小問1
(ヒント)
「N÷9」を小数第一位で四捨五入すると7になるので、「N÷9」の範囲は「小数第一位で四捨五入すると7になる数」の範囲と同じです。
「四捨五入すると~になる数」の解き方が分からない・忘れた人は以前の記事「四捨五入のやり方」を見て下さい。
以前と同じく3ステップで求めます。
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
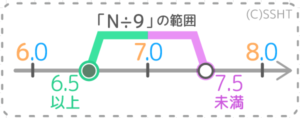
①小数第一位がゼロになるので目盛りは1刻み
②前後の目盛りは「6」と「8」で、がい数7と前後の目盛りの真ん中は「6.5」と「7.5」
③範囲は6.5以上7.5未満
と分かります。これが「Nを9で割った答え」=「N÷9」の範囲になります。
答: 6.5以上7.5未満
[/su_spoiler]
小問2
(ヒント)
「N÷9」を9倍すれば「N」になるので「N÷9の範囲」を9倍すれば「Nの範囲」になります。
ちなみに、範囲を倍にするときは、範囲の端の数字を倍にすればOKです。
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
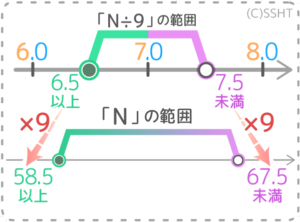
「N÷9」の範囲が「6.5以上7.5未満」なので端を9倍すると、6.5×9=58.5、7.5×9=67.5 より「58.5以上67.5未満」がNの範囲になります。
答: 58.5以上67.5未満
[/su_spoiler]
小問3
(ヒント)
小問2で求めた範囲内で、最小の整数と最大の整数を求めます
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
答: 最小59,最大67

[/su_spoiler]
「範囲を倍する」という考えが面白いですね?…ね?
(^_^;)
では、類題で練習しましょう
練習で定着!
類題1-1
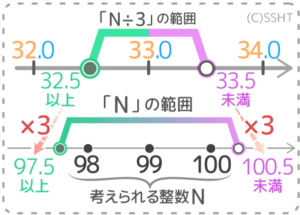
[su_spoiler title=”「N÷3」の範囲は?” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
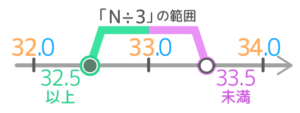
①目盛は1刻み(1,2,3…)
②33の前後の目盛りは「32」と「34」で
33と前後の目盛りの真ん中は「32.5」と「33.5」
③範囲は32.5以上33.5未満
これが「N÷3」の範囲になります。
[/su_spoiler]
↓
[su_spoiler title=”「N」の範囲は?” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
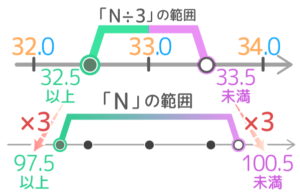
「N」は「N÷3」の3倍なので、「N÷3」の範囲(32.5以上33.5未満)を3倍すれば「N」の範囲が出ます。
32.5×3=97.5、33.5×3=100.5 なので「97.5以上100.5未満」がNの範囲になります。
[/su_spoiler]
↓
[su_spoiler title=”Nを求めると” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
この範囲内にある整数を全て書き出して…98,99,100の3つが答えです。
答: 98,99,100
[/su_spoiler]
慣れてきましたか?
もう一問解いてみましょう
類題1-2
(ヒント)
「Nはいくつか?」と聞かれている場合は、Nの範囲が非常に狭くて中に整数が一つしか無い場合です。
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
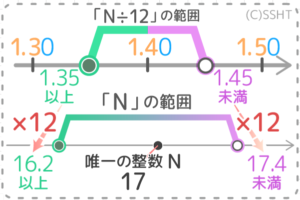
まず、「N÷12」の範囲(小数第二位で四捨五入すると1.4になる範囲)を求めます
①目盛りの細かさは0.1刻み
②1.4の前後の目盛りは「1.3」と「1.5」で、1.4と目盛りの真ん中は「1.35」と「1.45」
③「N÷12」の範囲は1.35以上1.45未満
↓
この12倍、1.35×12=16.2、1.45×12=17.4 より「16.2以上17.4未満」がNの範囲になります。
↓
この範囲内にある整数は17だけなので答えは17です。
答: 17
[/su_spoiler]
以上で「割られる数の復元」問題は終了です。
乗算からの復元(準備中)
企画構成中です(2020/2/10)
まとめ
●わり算の答えが概数として示される数
の範囲と最小・最大を求める問題
(例)9で割った答えを小数第一位で四捨五入すると
7になる数Nの最小最大を求める
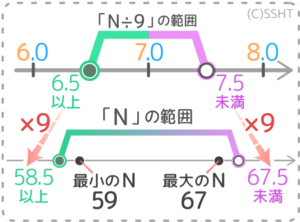
→割った答えの範囲を求めて(6.5以上7.5未満)
範囲の下限と上限を倍する(58.5以上67.5未満)
倍した範囲内の最大最小の整数(59,67)が答え

プリント
画像をクリックするとプリントが表示されますので保存して下さい。メアド等の入力は必要ありませんが、著作権は放棄しておりません。無断転載引用はご遠慮ください。
 爽茶
爽茶がい数の総合案内から他の記事も見て下さい
●
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ