「概数の応用問題にチャレンジしたい!」という小学4年生・中学受験生の方、お任せ下さい!東大卒講師歴20年の図解講師「そうちゃ」が入試でも出題される「概数同士の和と差」の問題を数直線で分かりやすく説明します!この記事を読めば似た問題がスラスラ解けるようになりますよ!
概数の基本が怪しい人はまず「四捨五入のやり方」を読んで下さい。
がい数の応用問題
概数の和と差
(整数の指定あり)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
考え方を理解♪
概数同士を足した大きさ(和)や引いた大きさ(差)を考える問題です。大きさに幅がある概数同士を足したり引いたりするので、結果にも当然幅が出来るのは予想できますね。
「整数」という指定がある場合とない場合で処理が異なるので、順に説明します。まずは概数に「整数」という指定がある場合です。まず例題で考え方を理解しましょう。
例題1(整数指定の和の最大最小)
以下の問いに答えなさい。
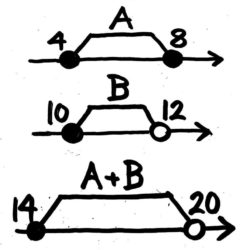
- Aが4以上8以下の整数でBは10以上12以下の整数である時、A+Bの最小・最大を求めよ
- Aが4以上8未満の整数でBは10以上12未満の整数である時、A+Bの最小・最大を求めよ
- Aが4以上8以下の整数でBは10以上12未満の整数である時、A+Bの最小・最大を求めよ
AとBが「整数」という指定があるので、AとBの最小値と最大値がハッキリと決まります。
したがってA+Bの最小・最大も値としてハッキリ決まります。
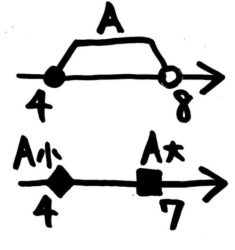
●例題1-(1)
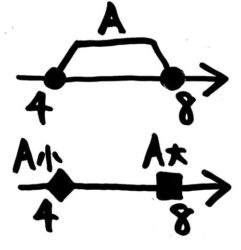
AとBの範囲を数直線上に表してみます。●は「以上」「以下」を、◯は「より大きい」「未満」を表します。忘れた人は((参考記事))を見直して下さい。
Aの最小値は4,最大値は8で、Bの最小値は10,最大値は12です。
したがって、A+Bの最小値は、最小値同士を足して4+10=14,A+Bの最大値は最大値同士を足して8+12=20と分かります。
最小同士と最大同士を合計します
答: 最小値14最大値20
このように、整数指定がある2つの概数の和の最大・最小は、最大値同士、最小値同士を合計すれば分かります。
概数の最小値同士、最大値同士で、概数の和の最小値、最大値を求められる。
((図))
(例)ABが整数で、4≦A≦8,10≦B≦12の時
→A+Bの最小値14,最大値20
小問2は範囲が変わります。
●例題1-(2)
Aの最小値は4,最大値は7です(8未満なので)、Bの最小値は10,最大値は11です(12未満なので)。

A+Bの最小値は、最小値同士を足して4+10=14,A+Bの最大値は最大値同士を足して7+11=18と分かります。
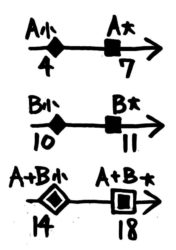
小問(1)とは最大値が異なります。
答: 最小値14最大値18
●例題1-(3)
分かってきましたか?
Aの最小値は4,最大値は8です(以下なので)、Bの最小値は10,最大値は11です(未満なので)。


Aは「以下」Bは「未満」
A+Bの最小値は、最小値同士を足して4+10=14です。一方、A+Bの最大値は最大値同士を足して8+11=19です。
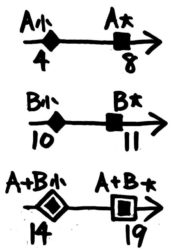
小問(1)とは最大値が異なります。
答: 最小値14最大値19
ABの最小同士、最大同士を足せば、何とかなりますね!では、問題を解いてみましょう。
練習問題で定着!
類題1
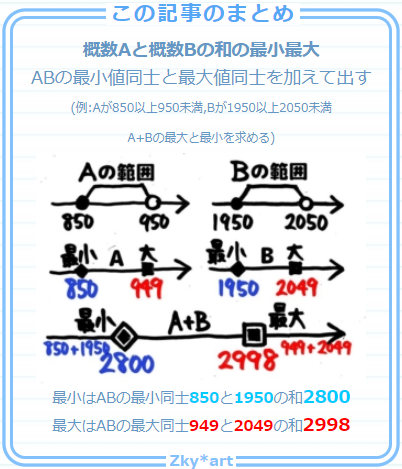
今度は範囲を出す必要があります。四捨五入の結果から元の数字の範囲を出す必要があります。やり方を忘れた人は、標準問題2(がい数の単純復元)を見直して下さい。
[su_spoiler title=”Aの範囲と最小値・最大値は?” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
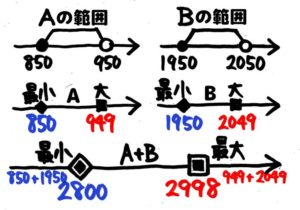
Aは850以上950未満なので、Aの最小値は850,最大値は949です。
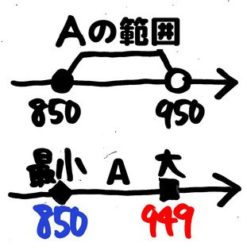
[/su_spoiler]
↓
[su_spoiler title=”Bの範囲と最小値・最大値は?” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
Bは1950以上2050未満なので、Bの最小値は1950,最大値は2049です。
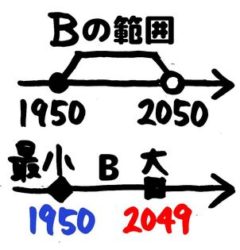
[/su_spoiler]
↓
[su_spoiler title=”A+Bの最小・最大は?” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
A+Bの最小値はAの最小値850+Bの最小値1950=2800です。一方、A+Bの最大値はAの最大値949+Bの最大値2049=2998です
答: 最小値2800最大値2998[/su_spoiler]
以上で概数の和の問題は終了です。できましたか?
引き算の場合
次は概数AとBの差(引き算)です。まず考え方を理解して下さい。
例題2(整数指定の差の最大最小)
以下の問いに答えなさい。
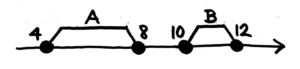
- Aが4以上8以下の整数でBは10以上12以下の整数である時、B-Aの最小・最大を求めよ
- Aが4以上8未満の整数でBは10以上12未満の整数である時、B-Aの範囲を求めよ
- Aが4以上8以下の整数でBは10以上12未満の整数である時、B-Aの範囲を求めよ
引き算(B-A)の場合は、ABの最小最大を同じ数直線上に並べて考えます。
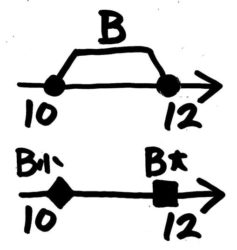
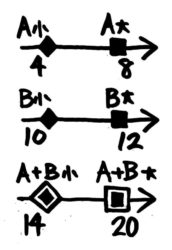
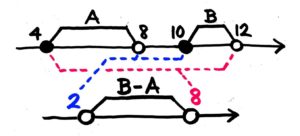
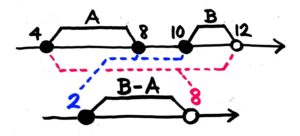
●例題2-(1)
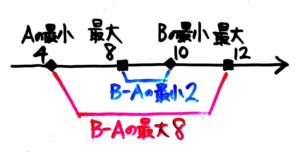
AとBの範囲と最小・最大は例題1と同じです。
B-Aが最小・最大になるのはどういう場合か、今度はABの最小最大を同じ数直線上に並べて考えます。
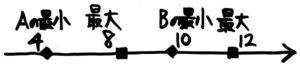
数直線上で2つの◆■の間の距離が一番短くなる場合が最小、一番長くなるのが最大です。どうなるでしょうか?
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
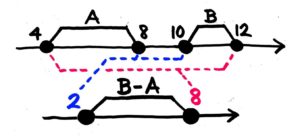
こうなりますね。一番近い同士を組み合わせすると差が最小に、一番遠い同士を組み合わせると差が最大になります。
B-Aの最小は、Bの最小10-Aの最大8=2です。一方、B-Aの最大は、Bの最大12-Aの最小4=8です。
答: 最小2 最大8[/su_spoiler]
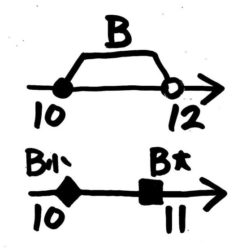
●例題2-(2)
ABの範囲と最小・最大は例題1のときと同じ
B-Aが最小・最大になるのはどういう場合か、さっきと同様に考えると?
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
B-Aの最小は一番近い点同士の組み合わせ(差)で、Bの最小10-Aの最大7=3です。一方、B-Aの最大は一番遠い点同士の組み合わせ(差)、Bの最大11-Aの最小4=7です。
答: 最小3 最大7[/su_spoiler]
●例題2-(3)
ABの範囲と最小・最大は例題1のときと同じ
B-Aが最小・最大になるのはどういう場合か、さっきと同様に考えると、
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
B-Aの最小は一番近い点同士、Bの最小10-Aの最大8=2です。一方、B-Aの最大は一番遠い点同士、Bの最大11-Aの最小4=7です。
答: 最小2 最大7[/su_spoiler]
このように、概数の引き算は2つの数の最大最小の点を4つ並べて、一番近い点同士の差、一番遠い点同士の差を求めれば良いのです。
最大最小の点を4つ並べて、一番近い点同士の差、一番遠い点同士の差を求めれば良い
では、類題で練習して下さい。
類題2
ここに考えるヒントや方針
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
[su_spoiler title=”AとBそれぞれの最小・最大は?” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
Aは850以上950未満なので、Aの最小値は850,最大値は949。Bは1950以上2050未満なので、Bの最小値は1950,最大値は2049。
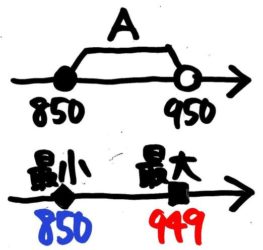

[/su_spoiler]
↓
[su_spoiler title=”B-Aの最小値・最大値は?” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
B-Aの最小値はBの最小値1950-Aの最大値949=1001です。一方、B-Aの最大値はBの最大値2049-Aの最小値850=1199です
答: 最小値1001最大値1199[/su_spoiler]
最後に足し算・引き算が混じった練習問題です。
練習問題1&2
(1)A+Bの最大・最小を求めよ
(2)A-Bの最大・最小を求めよ
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
Aの範囲は625以上635未満、Bの範囲は165以上175未満。
Aは最小625最大634で、Bは最小165最大174。
A+Bの最小は625+165=790 最大は634+174=808
答(1): 最小790,最大808
A-Bの最小は625-174=451 最大は634-165=469
答(2): 最小451,最大469
[/su_spoiler]
 爽茶
爽茶概数の和と差
(整数との指定なし)
次は「整数指定が無い」場合です。この場合は、最大・最小がハッキリ求められない場合があります。そのため、ここでは範囲を求める問題にしました。例題で処理手順に慣れてください
考え方を理解する♪
例題3(整数指定無しの和の範囲)
以下の問いに答えなさい。
- Aが4以上8以下でBは10以上12以下の時、A+Bの範囲を求めよ
- Aが4以上8未満でBは10以上12未満の時、A+Bの範囲を求めよ
- Aが4以上8以下でBは10以上12未満の時、A+Bの範囲を求めよ
●例題1-(1)
A+Bが一番大きくなるのはAの最大とBの最大を足した時、つまり 8+12=20です。一方、A+Bが一番小さくなるのはAの最小とBの最小を足した時、つまり 4+10=14です。
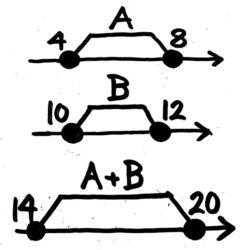
範囲の端は全て●になる
答: 14以上20以下
この場合は最小14最大20と答えられるので、整数指定があるのと同じ答えになります。次の小問は、条件が少し変わっています。どうなるでしょうか
●例題1-(2)
今度は「未満」なので、Aは最大でも 8にはギリギリなれず(◯になっています)、Bも最大でも12にギリギリなれません(◯になっています)。よって、A+Bは一番大きくなっても 8+12=20 にはギリギリなれません(20未満(◯)ということ)
一方、A+Bが一番小さくなるのは 4+10 で小問1と変わりません。
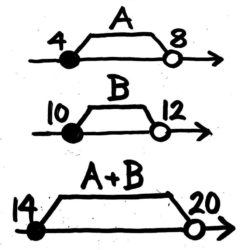
●+●は●に、◯+◯は◯になる
答: 14以上20未満
このように、整数指定が無い2つの概数の和の範囲は、概数の範囲の一番左(下限と言います)と一番右(上限と言います)同士を足したものになりますが、概数の範囲の端が●か◯かをよく見ないといけません。
概数の範囲の下限(左端)同士、上限(右端)同士、を足すと和の範囲が出る
((図))
(例)4≦A≦8,10≦B≦12の時
→14≦A+B≦20
次はこういう場合です。
●例題1-(3)
今度は、Bだけが未満になっています。この場合はどうなるでしょうか?
Aは最大で8になれますが、Bは最大でもギリギリ12にはなれません。よってA+Bの最大もギリギリ20にはなれません(未満(◯)ということ)。最小は小問(1)(2)と同じで 4+10 で14です。
●+◯は◯になります
答: 14以上20未満
考え方は分かりましたか?では、問題を解いてみましょう。
練習問題で定着!
類題3
まず、AとBそれぞれの範囲を求めましょう。あとは例題と同じです。
まずAの範囲とBの範囲を求めます。
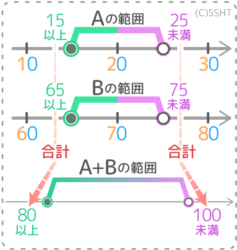
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
Aは15以上25未満、Bは65以上75未満です。

これが分からない人は標準問題2(がい数の単純復元)を見直して下さい[/su_spoiler]
↓
次にA+Bの範囲を求めます。例題で見たとおり、A+Bが一番小さくなるのはAもBも一番小さい時で、A+Bが一番大きくなるのはAもBも一番大きい時でした。計算してみましょう。
[su_spoiler title=”A+Bの範囲を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
下限同士は 15+65=80、上限同士は 25+75=100 より、A+Bの範囲は80以上100未満と分かります。
答: 80以上 100未満[/su_spoiler]
分かりましたか?次は差の問題です
差の場合
例題4(整数指定無しの差の範囲)
以下の問いに答えなさい。
- Aは4以上8以下、Bは10以上12以下の時、B-Aの範囲を求めよ
- Aは4以上8未満、Bは10以上12未満の時、B-Aの範囲を求めよ
- Aは4以上8以下、Bは10以上12未満の時、B-Aの範囲を求めよ
●例題1-(1)
AとBの範囲は例題1と同じですが、引き算なので横に並べてみます。
例題2で見たように、B-Aは2つの点の距離なので、B-Aが最小になるのは近い点同士の差で、Bの最小10-Aの最大8=2です。一方、B-Aが最大になるのは遠い点同士の差で、Bの最大12-Aの最小4=8 です。
B-Aの範囲の端は両方共●です
答: 2以上8以下
このように差を求める場合は最小と最大同士を引き算します。
B-Aの範囲は
「Bの最小-Aの最大」から
「Bの最大-Aの最小」になる
((図))
(例)4≦A≦8,10≦B≦12の時
→2≦B-A≦8
次の小問は、条件が少し変わっています。どうなるでしょうか
●例題1-(2)
Bの最小-Aの最大は、10-8 ですが、Aはギリギリ8になれない(7.~ということ)ので、Bの最小-Aの最大は2「より大きく」なります(図だと◯)。
Bの最大-Aの最小は、12-4ですが、Bはギリギリ12になれないので、Bの最大-Aの最小は8「未満」です(図では◯)
両方とも◯になっています。
答: 2より大きく8未満
●例題1-(3)
今度は、Bだけが未満になっていますが、もう分かりますね?
Bの最小-Aの最大は、10-8 で、Aは8になれるので、Bの最小-Aの最大は2「以上」です(図だと●)。
Bの最大-Aの最小は、12-4ですが、Bはギリギリ12になれない(◯)ので、Bの最大-Aの最小は8「未満」です(図では◯)
右端(上限)だけ◯になっています。
答: 2以上8未満
考え方は分かりましたか?では、問題を解いてみましょう。
類題4
ここに考えるヒントや方針
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
AとBの範囲は類題1と同じですが、差を求めるので同じ数直線上に並べてみます。

↓
B-Aの最小と最大はいくつになるでしょうか?
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
B-Aが小さくなるのは「Bの最小65」から「Aの最大25」を引いた時です。その差は 65-25=40 です。
同様にB-Aが大きくなるのは「Bの最大75」から「Aの最小15」を引いた時で、その差は 75-15=60と分かります。

しかし、ここで注意が必要です。「以上」(黒丸)と「未満」(白丸)を足したり引いたりした場合、計算の答えは「未満」や「より大きい」(両方とも白丸)になります。
従って
B-Aの範囲は「40『より大きく』60未満」になります。
答: 40より大きく60未満[/su_spoiler]
以上で「整数指定が無い」場合も終了です。お疲れさまでした!
 爽茶
爽茶●算数が苦手な人には「陰山メソッド 徹底反復 およそのかずプリント」
●中学受験の4・5年生には「算数の基本問題(小5)」(日能研)
●中学受験の6年生には「算数ベストチェック」(日能研)