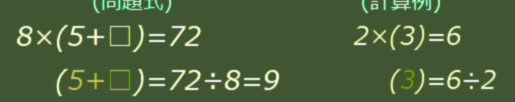逆算を間違えてしまう中学受験生の方「苦手だから、しょうがない…」と半分あきらめていませんか？
実は、たったひとつのコツをつかむだけで逆算のミスがあっという間に減るんですよ！
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が「計算例」を使った逆算のコツを分かりやすく教えます。
記事を真似すれば逆算のミスがなくなってクラスアップ・偏差値アップできるかも！
よくある逆算のやり方
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
番号をつける？→△
参考書でよく見かけるのが「計算の順序を数字で記入していく」というやり方です。
しかし、逆算は計算の逆順を行うものなので順序を書いてもかえってゴチャゴチャしてしまいます。
また、式全体ではなく「細部」に目がいってしまうので途中でミスをする可能性が高くなってしまいます。
公式で覚える？→△
また、「◆算の逆算は◇算」という覚え方もありますが、これは良くありません。
なぜなら、引き算・割り算の逆算は一種類の公式にできないからです。
それに配慮してか、親切なテキストでは、抽象的な記号を使った公式が載っていることもありますが…
足し算(●+○＝■)
→●=■ー○
→○=■ー●
正直、覚えにくくて混乱しますね…
じゃあどうするの？
ではどうするかというと…具体的な数字を使った「計算の例」を作って横に書くことを提案します！
二つの数の逆算(小3～)
爽茶では「計算の例」を使う解法を紹介します。
まず数字が二つの逆算を使って説明します。例えばこういう問題です
□を求めなさい
204-□=59
解けるよ！という人も少し読みすすめて下さい♪
解き方を理解♪
例題1-1(「計算例」の練習)
まず「全体として何算になっているか？」を考えます。
この計算は…引き算ですね。
引き算なので問題式の横にも簡単な「引き算」を書きます。
この「3-2=1」が「計算例」です！
さらに「計算例」に問題の式と同じ場所に□をつけます。
問題式は3つある数字(8,□,6)の真ん中が□なので、計算例も真ん中(ここでは2)を□で囲みます。
ここで、「計算例」を見て「真ん中の2を作るには左の「3」と右の「1」をどうすれば良いか」考えると…
「左(3)から右(1)を引く」と分かります。
2=
3–1
あとは、左にある問題式でも計算例と同じように「左(204)から右(59)を引く」を行うと答えが出ます！
□=
□=
204–59
145
2=
3–1
問題式でも行う
204-59で145です。□=145
今のやり方をまとめると、こうなります。
- 問題式と同じ形の計算例を横に書く
(問題式) (計算例)204-□=593-2=1 - 計算例で□の出し方を考える
(問題式) (計算例)204-□=593–2=
2=1
3–1左(3)ー右(1)で□が出る - 問題式で同じことをすると答が出る。
(問題式) (計算例)204-□=
□=
□=59
204–59
1453–2=
2=1
3–1同じように「左」ー「右」をする
もう1問やってみましょう。
「➊計算例を横に書く→❷計算例で□の出し方を考える→❸問題式で同じことをする」で進めましょう。
例題1-2(「計算例」の練習)
➊計算例を横に書く
問題の式全体を見ると引き算なので、横に「引き算」の計算例を書きます。
➋□の出し方を考える
計算例で□の出し方を考えると、真ん中(2)+右(1)と分かります。
3=
2+1
❸問題式で同じことをして答を出す
問題式でも「真ん中(95)と右(87)を足す」と□がでます。
□=
□=
95+87
182
3=
2+1
95+87で182 です。182
「計算例」を書くことで、逆算が何算になるのか簡単に分かりました♪
学習時には書くことが大事
ここで大切なのは計算例を実際に「書く」ことです。
逆算が「分からない」という生徒はほとんどいません。「分かっているけど本番ではミスする」のです。
ミスを防ぐためには「作法」を決めて日常の学習時に練習しておかないといけません。
ここでは「計算例を横に書く」というのが「作法」にあたります。
計算例を決めておく
前もって「計算例」を決めておき問題の横に書く習慣をつけると苦手な生徒さんでも確実に解けます♪
私が自分の生徒に作らせる例を示します(「1+1=2」のように同じ数を2回使わないように気をつけます)
足し算：3＋2=5
引き算：3ー2=1
かけ算：3×2=6
割り切り算：6÷3=2
割り余り算：7÷3=2…1
「3→2」と始まるものが多いので覚えやすいと思います。
今回はこの例を使っていきましょう
余りのある割り算の逆算
この中で、余りのある割り算(割り余り算)だけは少し難しいかもしれないので説明をしておきます。
左端の7が□の場合は、3×2+1で求め
7=
3×2+1
中左の3が□の場合は(7-1)÷2で求めます
3=
(7-1)÷2
では、色々な計算で試してみましょう！
練習問題で定着！
●類題1-1
全体を見ると「足し算」なので、足し算の計算例「3+2=5」を横に書きます。
問題式と同じく□を真ん中につけて、□の出し方を考えると、5(右)ー3(左)です。
2=
5-3
同じことを問題式でも行えば答えです。
□=
□=
517-435
82
2=
5-3
82
●類題1-2
全体を見ると「かけ算」なので、かけ算の計算例「3×2=6」を横に書きます。
問題式と同じく□を左端につけて、□の出し方を考えると、6(右)÷3(真ん中)です。
2=
6÷3
同じこと(右÷真ん中)を問題式でも行えば答えです。
□=
□=
152÷19
8
2=
6÷3
82
ちなみに、かけ算の場合、□が左端でも真ん中でも計算は割り算になります。(この事を暗記する必要はありません)
●類題1-3
余りのない割り算(割り切り算)です。
全体を見ると「割り切り算」なので、割り切り算の計算例「6÷3=2」を横に書きます。
問題式と同じく□を左端につけて、□の出し方を考えると、3(真ん中)×2(右)です。
3=
3×2
同じこと(真ん中×右)を問題式でも行えば答えです。
□=
□=
14×21
294
3=
3×2
294
●類題1-4
同じ割り切り算ですが…
前問と同じく、割り切り算の計算例「6÷3=2」を横に書きます。
問題式と同じく□を真ん中につけて、□の出し方を考えると、6(右)÷2(左)です。前問と違い割り算になりました。
3=
6÷2
同じこと(右÷左)を問題式でも行えば答えです。
□=
□=
112÷7
16
3=
6÷2
16
●類題1-5
余りのある割り算(割り余り算)です。□の求め方を少し考える必要があるかもしれません
全体を見ると「割り余り算」なので、割り余り算の計算例「7÷3=2…1」を横に書きます。
問題式と同じく□を左端につけて、□の出し方を考えると、3(中左)×2(中右)+1(右端)になりますね。
7=
3×2+1
同じこと(中左×中右+右端)を問題式でも行えば答えです。
□=
□=
8×9+6
78
7=
3×2+1
78
余りのある割り算での計算例の使い方が分からない・忘れたという人は上の方にあるココを見直すと良いでしょう。
●類題1-6
また割り余り算ですが…
前問と同じく、割り余り算の計算例「7÷3=2…1」を横に書きます。
問題式と同じく□を中左につけて□の出し方を考えると、{6(右端)-1(左端)}÷2(中右)です。
3=
(7-1)÷2
同じこと{(右端)-(左端)}÷(中右)を問題式でも行えば答えです。
□=
□=
(263-3)÷20
13
3=
(7-1)÷2
13
爽茶三つの数の逆算カッコあり
(受験小3)
爽茶次は数字が三つとカッコがある計算の逆算です。
こういう問題です。
□を求めなさい
5×(□-3)=30
解き方～カッコの中を空にする
例題2(三数の逆算カッコあり)
まず問題式全体を見て、この式全体が何算になっているか考えます。コツはカッコの中が空白だと考えることです(ここでは色を薄くしています)。
5×(□-3)=30
かっこの中が空白だと考えると
「5」と「( )」2つのカタマリになる
こうすると全体が「5」と「( )」の二つのカタマリになって「かけ算」と分かります。このように、常に二つのカタマリにして考えるのがコツです。
「かけ算」と分かったので計算例「2×3=6」を書き、問題式と同じ位置にカッコをつけます。
(問題式) (計算例)
計算例にもカッコをつける
ここでカッコ数字「(3)」を作るのにどうすればよいか考えると「右(6)÷左(2)」と分かるので、問題式でも同じように「右÷左」でカッコ「(□-3)」を計算します。
(問題式) (計算例)
(□-3)=
30÷5=6
(3)=
6÷2
左端÷右端で
カッコの中身が分かった
これで(□-3)は6と分かりました。カッコの中と計算結果だけを下に書き移します。
(問題式) (計算例)
(□-3)=
□-3=
30÷5=6
6
(3)=
6÷2
単純な逆算になった♪
これで「□-3=6」という基本的な二数の逆算になりました。あとは今までと同じです。
全体では何算か考えて、計算例を横に書き□の出し方を考えて、同じことを問題式でもすれば□が出て終了です。
(問題式) (計算例)
(□-3)=
□-3=
□=
30÷5=6
6
6+3=9
(3)=
3-2=
3=
6÷2
1
1+2
( )を出す→□を出す。の順序で
□は9と分かりました。9
このように、□がカッコの中にある時はまずカッコを求めて、次に□を出します。
- カッコの中を空白にして二数の逆算にする
5×(□-3)=30
かっこの中が空白だと考えると
5と( )の2つのカタマリになる - カッコを求める
(問題式) (計算例)
5×(□-3)=
(□-3)=30
30÷5=62×(3)=
(3)=6
6÷2カッコの中身が分かった
- カッコの中を戻して□の逆算にする
(問題式) (計算例)
5×(□-3)=
(□-3)=
□-3=30
30÷5=6
62×(3)=
(3)=6
6÷2単純な逆算になった♪
- □を出して終了
(問題式) (計算例)
5×(□-3)=
(□-3)=
□-3=
□=30
30÷5=6
6
6+3=92×(3)=
(3)=
3-2=
3=6
6÷2
1
1+2( )を出す→□を出す。の順序で
では練習問題で定着して下さい。
練習問題
対象：小3以上
●類題2-1-(1)
途中はこうなって…
(問題式) (計算例)
(5+□)=
5+□=
□=
72÷8=9
9
9-5=4
(3)=
2+3=
3=
6÷2
5
5-2
( )を出す→□を出す。の順序で
□=4
●類題2-1-(2)
途中はこうなって…
(問題式) (計算例)
(24-□)=
24-□=
□=
63÷7=9
9
24-9=15
(3)=
3-2=
2=
6÷2
1
3-1
初めが割り算ですが同じですね♪
□=15
●類題2-1-(3)
途中はこうなって…
(問題式) (計算例)
(45-□)=
45-□=
□=
42÷7=6
6
45-6=39
(3)=
3-2=
2=
6÷2
1
3-1
だいぶ慣れてきたのでは？
□=39
●類題2-1-(4)
途中はこうなって…
(問題式) (計算例)
(2+□)=
2+□=
□=
36÷4=9
9
9-2=7
(2)=
3+2=
2=
6÷3
5
5-3
カッコが初めにあるパターンです
□=7
●類題2-1-(5)
こうなります。
(問題式) (計算例)
(□-22)=
□-22=
□=
8×5=40
40
22+40=62
(6)=
3-2=
3=
3×2
1
2+1
カッコが初めにあるパターンです
□=62
●類題2-1-(6)
余りのある割り算の計算例はこうでした
3=
(7-1)÷2
途中はこうなります
(問題式) (計算例)
(263-□)=
263-□=
□=
(51-2)÷7=7
7
263-7=256
(3)=
3-2=
2=
(7-1)÷2
1
3-1
□=256
爽茶カッコがある逆算は以上です。
三つの数の逆算
カッコなし(受験小3)
爽茶今度は、カッコが無い三つの数を計算する逆算をときます。
一番多いのが+ーと×÷が混じった、こういう問題です。
□を求めなさい
31ー□×2＝17
解き方～カッコをつけよう
当ブログでは普通の計算のときにも「かけ算・割り算には自分でカッコをつけよう」と指導しています。興味がある人は関連記事「計算ミスをゼロにする3つの作法」を見て下さい。
6＋(16÷2)=□
実は逆算を解くときにも「かけ算・割り算には自分でカッコをつける」のが簡単に解くコツです。
31ー(□×2)＝17
こうすることで「31」「□」「2」という三つの数字の計算だったのが「31」と「(□×2)」という二つのカタマリになって、全体として何算か分かりやすくなるんですね。
あとはさっきと同じように、❶まずカッコを出して❷次に□を出せばOKです。
では、このやり方で答えを出してみましょう。
例題3-1
かけ算わり算にカッコを付けて、カッコの中が空白だと考えると(ココでは色を薄くします)、全体が2つのカタマリになるので、全体として何算になるか考えて…
31-(□×2)=
17
全体としては「引き算」と分かる
「計算例」を横に書き、問題式と同じ場所にカッコをつけます
31-(□×2)=
17
計算例を見てカッコの出し方が「真ん中(2)=左3ー右1」と分かったら、同じ計算「真ん中(□×2)＝左31ー右17」でカッコを計算します。
31-(□×2)=
(□×2)=
=
17
31–17
14
(2)=
3–1
カッコの値が分かったら一行下にカッコの中と値を書き直すと二数の逆算の問題が出来ました。
(□×2)=
(□×2)=
31-17
14
(2)=
3-1
ここからは、単純な逆算の問題を解きます。横に「計算例」を書き□を付け足します。
31-(□×2)=
(□×2)=
(□×2) =
17
31-17
14
(2)=
3×2=
3-1
6
計算例を見れば「3＝左6÷真ん中2」と分かるので、同じように「□＝左14÷真ん中2」で答えが出ます。
31-(□×2)=
(□×2)=
(□×2) =
□=
=
17
31-17
14
14÷2
7
(2)=
3×2=
3=
3-1
6
6÷2
□は7ですね。7
今の問題は「+－(足し算引き算)」と「×÷(かけ算割り算)」が混じっていたので「×÷」をカッコに入れました。
では「×÷(かけ算割り算)」しかない三つの数の計算ではどうすればよいでしょうか？
例題3-2
かけ算割り算しかない場合は前の二つをカッコに入れて大きな2つのカタマリにしてしまいます。
(32÷□)×5=
20
かけ算とわかります。
こうすれば全体としては「かけ算」だと分かるので、かけ算の計算例を書いて…
(32÷□)×5=
20
カッコを求めたら…
(32÷□)×5=
(32÷□)=
(32÷□)=
20
20÷5
4
(2)=
6÷3
□も計算例を書いて計算方法を考えて…
(32÷□)×5=
(32÷□)=
(32÷□)=
□=
=
20
20÷5
4
32÷4
8
(2)=
6÷3=
3=
6÷3
2
6÷2
8と分かります。8
最後に、数が三つで「+－(足し算引き算)」だけの場合はどうすればよいでしょうか。
例題3-3
足し算引き算しかない場合も前の二つをカッコに入れて大きな2つのカタマリにすればOKです！
(13-□)+12=
15
足し算になりました。
あとはいつものやり方で解けますね。
まず、カッコを求めて…
(13-□)+12=
(13-□)=
=
15
15-12
3
(2)=
5-3
□を出して終了です。
(13-□)+12=
(13-□)=
(13-□)=
□=
=
15
15-12
3
13-3
10
(2)=
3-2=
2=
5-3
1
3-1
□は10です。10
このように、カッコがない三つの数の逆算は二つをカッコに入れるところからスタートします。そしてカッコに入れる二つの数の決め方が二通りあります。
まとめるとこうなります。
- 三つのうち二つをカッコに入れる
- カッコの値を求める
- □を求める。
<カッコに入れる二つの数の決め方>
◆足し算引き算とかけ算割り算が混ざっている場合
→かけ算割り算をカッコに入れる。
(例)31-□×2=17 → 31-(□×2)=17
◇足し算引き算だけ、かけ算割り算だけの場合
→前の2つをカッコに入れる。
(例1)32÷□×5=20 → (32÷□)×5=20
(例2)13-□+12=15 → (13-□)+12=15
では問題で練習しましょう。
練習問題で定着！
●類題3-1
わり算をカッコに入れて、スタートします。
25+(□÷8)＝
(□÷8)=
□÷8=
□=
31
31-25=6
6
8×6=48
(2)=
6÷3=
6=
6÷3
2
3×2
48
●類題3-2
かけ算をカッコに入れてスタート
(4×□)-19=
(4×□)=
4×□=
□=
9
19+9=28
28
28÷4=7
(3)=
2×3=
3=
2+1
6
6÷2
7
●類題3-3
割り算をカッコに入れてスタート
76-(72÷□)=
(72÷□)=
72÷□=
□=
68
76-68=8
8
72÷8=9
(2)=
6÷3=
3=
3-1
2
6÷2
9
●類題3-4
かけ算わり算しかないので前の二つをカッコに入れます。
かけ算わり算しかないので前の二つをカッコに入れてスタートします。
(8×□)÷4=
(8×□)=
8×□=
□=
6
4×6=24
24
24÷8=3
(6)=
2×3=
3=
3×2
6
6÷2
3
●類題3-5
足し算引き算しかないので前の二つをカッコに入れます。
足し算引き算しかないので前の二つをカッコに入れてスタートします。
(324+□)-256=
(324+□)=
324+□=
□=
147
256+147=403
403
403-324=79
(3)=
2+3=
3=
1+2
5
5-2
79
●類題3-6
余りのある割り算で「割られる数」の計算例はこうでしたね。
7=
3×2+1
かけ算割り算しかないので、はじめの二つをカッコにいれると、全体としては「余りのある割り算」になります。
(8×□)÷9=
6…2
「余りのある割り算」の「割られる数」は、かけ算と足し算で求めました。
(8×□)÷9=
6…2
(7)=
3×2+1
あとはカッコを出して、□を出して終了です。
(8×□)÷9=
(8×□)=
8×□=
□=
=
6…2
9×6+2
56
56÷8
7
(7)=
2×3=
3=
3×2+1
6
6÷2
7
爽茶四つ以上の数の逆算(受験小4～)
数字が四つ以上の逆算も考え方は同じです。
例題4-1(カッコなし1:2:1)
39+12×□ー53=70
39+(12×□)ー53=
(39+(12×□))ー53=
(39+(12×□))=
39+(12×□)=
(12×□)=
12×□=
□=
□=
70
70
53+70
123
123-39
84
84÷12
7
(3)=
1+(2)=
(2)=
2×3=
3=
2+1
3
3-1
6
6÷2
例題4-2(完全フラット)
81+□－71+65=99
(81+□－71)+65=
(81+□－71)=
(81+□)-71=
(81+□)=
81+□=
□=
□=
99
99-65
34
71+34
105
105-81
24
(1)=
(3)-2=
(3)=
1+2=
2=
3-2
1
2+1
3
3-1
このように、数が4つ以上になっても、2つのカタマリにしたら計算例を書いてカッコを求めて…を繰り返して□が出たら終わりです。
- かけ算・わり算をカッコに入れる。
- 大きなカタマリ2つになるようにカッコにいれる。
- 全体として何算か考えて「逆算例」を横に書く
- カッコの中を空白にしてカッコを求める
- カッコの中を書く(❸に戻る)
- □が出たら終了
もっと問題を解きたい」人は関連記事「四数以上の逆算」を見て下さい。
小数と逆算(受験小4～)
小数が入ると暗算で求めるのが難しくなるので、計算例を書いて確実に解きましょう。
小数の計算自体を素早く正確にできることも必要です(自信がない人は姉妹サイト「そうちゃ式 旧館」の「小数のまとめ」内の小数計算のまとめを見て下さい)。
小数の逆算を解きたい人は参考記事「小数のある逆算」を見て下さい。
分数と逆算(受験小5～)
分数が入った逆算で通分計算があると暗算で求めるのはかなり難しくなるので、計算例を書かいて確実に解きましょう。
分数の計算自体を素早く正確にできることも必要です(自信がない人は姉妹サイト「そうちゃ式 旧館」の「分数のまとめ」内の分数計算を見て下さい)。
分数の逆算を解きたい人は参考記事「分数のある逆算」を見て下さい。
爽茶逆算の説明はこれで終了です！
●「計算でる順」(旺文社)
●「逆算の特訓」(上)(下)(サイパー算数)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!