相当還元算が難しい!」という中学受験生の方、確かに割合の計算がややこしかったり、線分図を書くのが大変かもしれません
でも安心して下さい。基本の割合を図に表すことができるなら、ちょっとコツを覚えるだけで線分図も書けるようになりますよ!
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が割合の「矢印図」から「線分図」を書く方法と答えの出し方を分かりやすく説明します。
記事を真似して図を書けば、相当還元算が苦手ではなくなっているでしょう♪
目次で「還元算」など好きな場所をクリックするとジャンプできますよ。
割合(復習)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
相当算・還元算は「割合」の一分野なので、割合を簡単に復習します!「AのB倍はC」「CはAのB倍」という関係がある時に「矢印図」を使います。
(矢印図)
→3つの数が「A×B=C」の関係にある時に、
矢印の向きに沿って「A」「B」「C」を並べた図
(例)「2の3倍は6」「6は2の3倍」→「2×3=6」の矢印図になります。
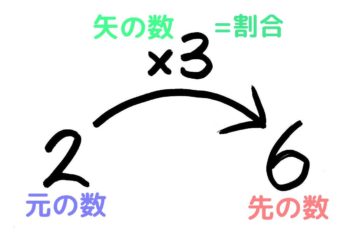 2×3=6の図
2×3=6の図
逆向きの矢印を追加します。
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
矢印図から線分図へ
矢印図で解く
「相当算・還元算」は矢印図の「先の数」から「元の数」を求める問題。
例えば「月に行きたいという生徒は231人で、これは全校生徒の33%にあたる。全校生徒数は何人ですか?」という問題です。
「231人は全校生徒の33%にあたる」は「全校生徒×0.33=231人」と同じなので、矢印図では反対の矢印を追加して解きます。
の矢印図
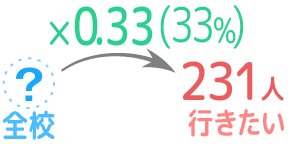
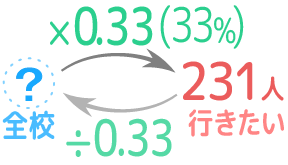
?=231÷0.33=700と解く
線分図で解く
このような単純な問題なら矢印図でも解けますが、この先の応用問題を解くには線分図を使う方が分かりやすいので、線分図でも解いてみます。
まず全校生徒を①(マルイチ)として線分を書き、その33%(だいたい三分の一の長さ)を区切ります。
33%=0.33なので区切った部分に「0.33」と書き、その下に「行きたい」などの文字と「231人」を書き足します(図1)。この線分図は矢印図(図2)と同じことを意味しています。
これは全校生徒の33%にあたる。」

を図にしたもの
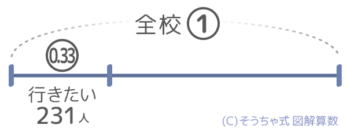
33%にあたる231人を0.33とする。
そして「0.33=231」のような「丸数字=数値」という関係が見つかったら、「数値÷丸数字」という計算をすると①が求められます。この場合は231÷0.33=700=①で、これが答です(図3)。矢印図(図4)でも同じ計算をしていますね。
これは全校生徒の33%にあたる。
全校生徒は何人か?」


数値÷丸数字を計算すると①が分かる。矢印図でも
同じ計算「231÷0.33」をしているのに注目
これが線分図を使った相当算の解き方です。
図を書くと時に全体を「1」ではなく「①」と書いて、単位がある普通の数値と区別するのが大切です。
- 全体(元の数)を①として線分図を書く
- 「丸数字=数値」という関係を見つける。
- 数値÷丸数字で①を求める。
この「数値÷丸数字で①を求める」というのは受験算数の基本作業で「分配算」でも使いましたね。
テストで試してみましょう
クッキーが缶に詰められています。26個を食べました。全体の1320に当たるとき、はじめ何個のクッキーが入っていましたか。
→( 全体①とすると1320が26個なので「1320=26」よって①=26÷1320=26×2013=2×201=40個 )
「残り」から求める問題
問題文には直接書いていない「残りの割合」を使う問題です。
「残り」の割合
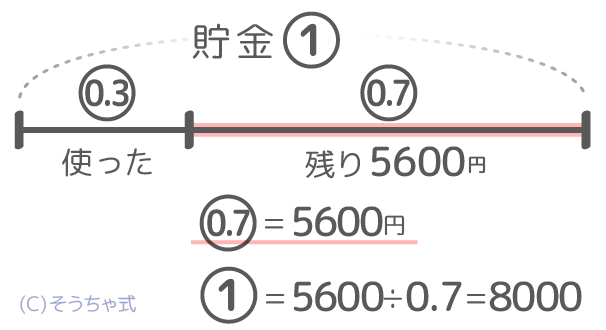
例えば「貯金の3割を使ったら5600円が残った。最初、貯金はいくらあったか?」という問題です。
さっきのルールで線分図を書きますが、これだけでは「丸数字=数値」という関係がみつかりません(図1)。
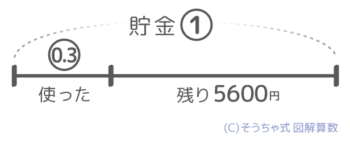
そこで問題文には書いていない「残りの割合」を自分で求めて書き込みます。全体が①で使ったのが3割=0.3ですから残りは①ー0.3=0.7(7割)で、これが5600円です(図2)。

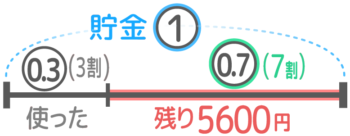
は同じ内容を表している
0.7=5600という関係が見つかったので、5600÷0.7=①=8000円が最初の貯金額と分かります。

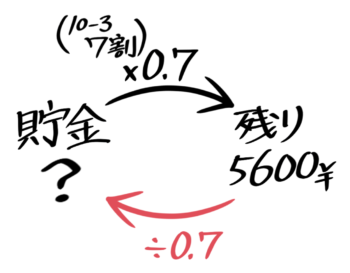
同じ計算(5600÷0.7)をしている
練習問題をどうぞ
2-1:残り相当算
解説
インフルエンザにかかっていない残りの322人は92%=0.92に相当します
登校したのは322人
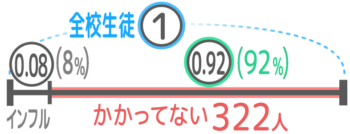
全体①=322÷0.92=350人です
次は、使う量が「半端」な場合です。
端数がある場合
使う量に半端な数がある場合を考えます。プラスとマイナス2つの場合があります
半端な数(プラス)の場合
例えば「貯金の2割より2000円多く使ったら10000円が残った。最初、貯金はいくらあったか?」という問題です。
線分図を書きます。貯金全部を①、2割が0.2ですが、まだ「丸数字=数値」という関係が分かりません。
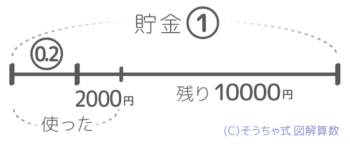
そこで①-0.2=0.8を書き込むと、0.8=2000+10000=12000円という関係が見つかりました(図2)
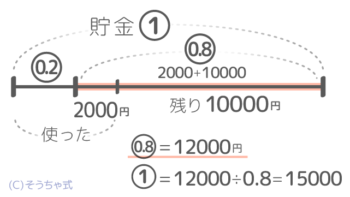
これで12000÷0.8で①=15000円と分かります。
半端な数(マイナス)の場合
半端な数がマイナスの場合もあります。
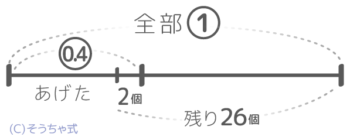
例えば「箱に入ったたくさんのお菓子の4割より2個少ない個数を友達にあげたら26個残った。最初お菓子は何個あったか?」という問題です。
これも線分図を書きます。お菓子全部を①、4割が0.4、2個、26個という問題文の言葉・数値に加え①-0.4=0.6を書き加えて観察すると0.6=26-2=24という「丸数字=数値」の関係が分かります。
書いた図
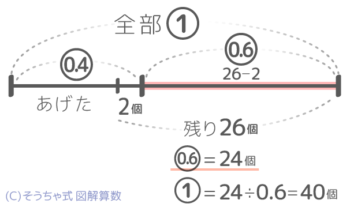
これで①=24÷0.6=40個と答が出せます。
確認テスト(2020.2.22作成中)
端数ある二分割
「残り」ではない、端数の書き方を使った別タイプの問題を解いてみます。
全体の集団が二種類に分けられるときに、それぞれが端数で表現される問題で「端数ある二分割」と呼びます
「多い・多い」タイプ
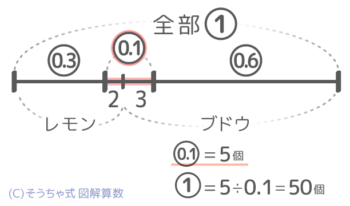
例えば「袋の中にレモン味とブドウ味のアメがたくさん入っている。レモン味のアメは全体の3割より2個多く、ブドウ味のアメは6割より3個多い。アメは全部で何個あるか?」という問題です。
線分図を書いてみます。二種類のアメしか無いのでレモン(0.3+2)とブドウ(0.6+3)ですき間なく①になります。

線分図をながめると、丸数字のすき間①-(0.3+0.6)=0.1が5と等しいのが分かります。「丸数字=数値」を見つけたので、数値÷丸数字で①=5÷0.1=50と分かります。
確認テストをどうぞ
ある小学校の男子の人数は全校生徒の52%より21人多く、女子は40%より15人多い。全校生徒は何人か?
→( 100-(40+52)=8%=0.08が21+15=36人にあたるので、全体①=36÷0.08=450人 )
「少ない・少ない」タイプ
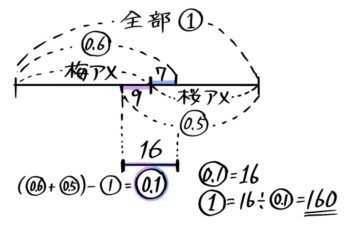
「梅アメと桜アメがたくさん入った袋がある。梅アメは6割より7個少なく、桜アメは5割より9個少ない。アメは合計何個あるか?」
全体を①、梅アメの線分図を0.6-7個の長さで区切ります。すると桜アメの個数もここまでとなります。
そして桜アメが0.5-9個になるように0.5を書くと、梅で書いた0.6と重なってしまいます。これがポイントです。
そもそも0.6+0.5=1.1なので0.1の重なりができるのですね。この0.1が7+9=16と等しいと気付ければ、①=16÷0.1=160と分かりますね!
確認テスト(作成中)
「多い・少ない」タイプ
2023.9.3作成中
二回・三回の相当算
例題1(二回の相当算)
本を買って1日目は全体の2割を、2日目は全体の25%を読んだところ、あと121ページ残っている。本は全部で何ページあるか
本全体を①とすると、1日目に読んだのは0.2、2日目に読んだのは0.25になります。
したがって、残り121ページは1-(0.2+0.25)=0.55に相当するので
①=121÷0.55=220ページです
例題2(三回の相当算)
今の問題は「はじめの」量を基準に数量を計算しましたが、次は残りを基準に計算します
二段の相当算
ここまでの相当算は一回の計算で(一段階で)①が出せましたが、問題文が複雑になってくると一回では①が出せなくなってきます。
「残りの」○割
例えば「昨日貯金の4割を使ってゲームソフトを買い、今日は残りの3割でフィギュアを買ったところ6300円残った。最初貯金はいくらあったか?」という問題です。
全体(最初の貯金)を①、昨日使ったのが0.4、そして今日使ったのは「残りの」3割なので0.3ではありません(それだと最初の貯金の3割になってしまいます!)(図1)。
そこで、昨日の残り0.6を新しい記号で1とおき、今日使った金額を0.3と書きます(図2)。
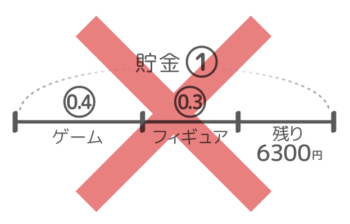
フィギュアは0.3ではない
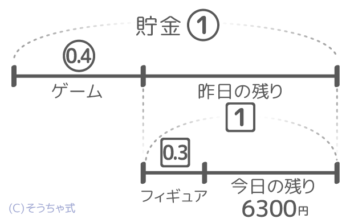
新しい記号を作って0.3とする
すると最後に残るのは1ー0.3=0.7で、これが6300円です。(図3)。
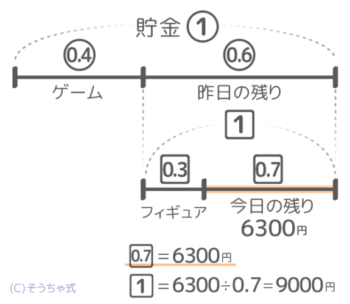
丸数字ではありませんが「記号数字=数値」が分かったので、6300÷0.7で1=9000円と求められます。これは0.6でもあるので、0.6=9000円です。やっと「丸数字=数値」が分かりました(図4)。
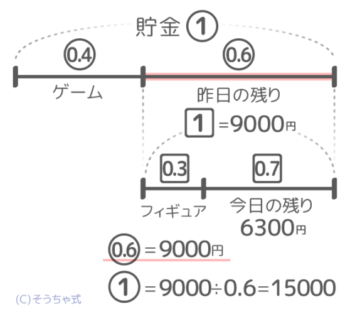
「1=0.6=9000」を使う
あとは9000÷0.6=15000円=①で、最初の貯金は15000円と分かります!
このように元の数が2つ出てくる(記号数字が二種類以上出てくる)問題の解き方をまとめると次のようになります。
- 全体を①、一部の丸数字を1として線分図を書く。
- 「四角数字=数値」を見つけ、数値÷四角数字で1を求める
- 数値(1の値)÷丸数字で①を求める。
確認テスト(2020.2.18作成中)
記号を一種類ですませる
記号が2種類あるのが面倒くさい!という人は次のように一種類の記号だけで解くことも出来ます。
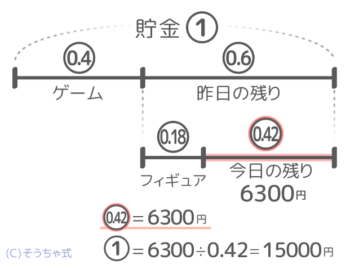
フィギュアの値段は、昨日の残り0.6の3割(×0.3)なので0.6×0.3=0.18とも表せます(図1)。
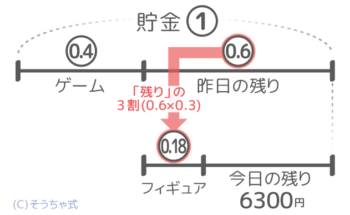
割合×割合をすれば良い
すると今日残っている金額も0.6-0.18=0.42と表せて、これが6300円なので「0.42=6300」と分かります。ここから①=6300÷0.42=15000と答が出せます(図2)。
確認テスト(作成中)
端数のある二段相当算
半端な数の残りのさらに○割という面倒な問題も丁寧に図を書けば還元算で解けます。
例えば「ある本を一昨日は全体の4割より3ページ多く読み、昨日は残りの半分より3ページ少なく読んだところ30ページ残った。全部で何ページあるか?」という問題です。
ニ種類の記号で解くのが基本
一日目に読んだ量は0.4+3で、一日目の残りをもう一つの記号を使って1とおきます。
すると、二日目に読んだ量は0.5-3、最後に残ったのが30ページという図が書けます(図1)。
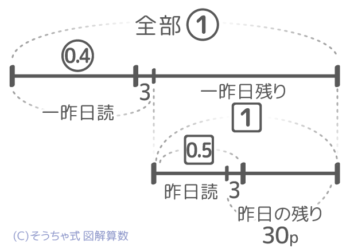
問題文の数値を図にしたところ
線分図を見て0.5=30-3=27ページと分かれば1が27÷0.5=54ページと分かります。これを線分図に書き込み「丸数字=数値」の関係を探します。
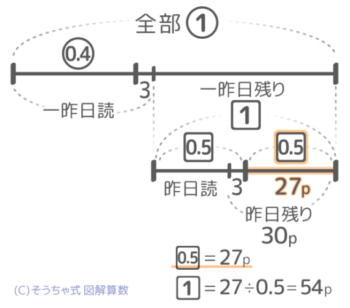
1(一昨日の残り)を求める
「0.6=54+3=57ページ」と気づけば、①も57÷0.6=95ページと分かりますね。
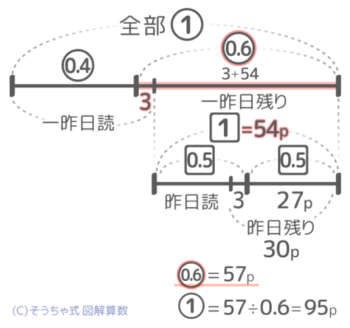
①を求めて終~了~♪
端数のある場合を一段階で解く
上の問題を一種類の記号で解くには少しテクニックを使います。
一日目の残りを「0.6-3」と表して、二日目に読んだ量を{(0.6-3)×0.5}-3=0.3-1.5-3=0.3-4.5 と計算します(0.6と3の両方に0.5をかけるのと-4.5になるのに注意)
線分図を眺めて、丸数字のすき間が①-(0.4+0.3)=0.3で、これが3+(30-4.5)=28.5ページだと気づけば、28.5÷0.3=95と求めることができます。
ただ、これは線分図も計算もやや複雑で計算ミスの可能性も増えるので、還元算でニ種類の記号を使ったほうが良いかもしれませんね。
三段の相当算
次は線分図が三段!になる場合です
端数が無い場合
端数がない場合は、1種類の記号だけでも解けますが、まずは3種類の記号を使う方法をマスターして下さい
三種類の記号で解く
例題
Aは1日目に所持金の3割をBにあげ、2日目に残りの40%をCにあげ、3日目に残りの45をDにあげたところ、420円残った。はじめの所持金は何円だったか?
所持金を1、1日目の残り(①の7割=0.7)を1、2日目の残り(1の60%=0.6)を1とおいた、3つの記号で線分図を書きます
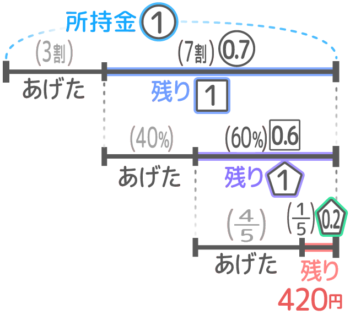
一番下の三段目の線分図から1→1→1の順に求めていく。
3日目の残り420円=0.2なので、1(2日目の残り)=420÷0.2=2100円
12100円=0.6なので、1(1日目の残り)=2100÷0.6=3500
13500円=0.7なので、1(所持金)=3500÷0.7=5000円です
少ない種類の記号で解く
算数が好き/得意な人はコチラもできるようにしておくと良いでしょう。
端数がある三段
端数がある場合は三種類の記号を使うのをオススメします。
例題(2020.4.10作成中)
他の割合分野「売買算(損益計算)」「濃度」にも挑戦してみましょう!
オススメ教材
 爽茶
爽茶●相当算だけを解きたい場合は「基本の制覇 相当算・仕事算・倍数算」(グノーブル)
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題」シリーズ(日能研)
●小6受験生には「算数ベストチェック」(日能研)
「分かりやすい!」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては?
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ