「売買損益算が難しい！」という中学受験生の方、そのとおり！です…
実は売買損益算は「1個の品物の問0題」「多くの品物の販売の問題」という解き方が別の2つのパートから出来ているので普通の特殊算の2倍のボリュームがあるんです！
そのため「1個の品物を売る場合」→「多数の品物を売る場合」の順に確実に解き方を学ばないと途中で分からなくなってしまいます(汗)
「大変だなぁ…」と思ったかもしれませんが、安心して下さい！
この記事では東大卒講師歴２０年の図解講師「そうちゃ」が売買損益の2つのパートを順番に分かりやすく説明します。
5年の一学期までに前半を、夏休み中に後半を学習すれば良いでしょう。
記事を読んで例題を解けば売買損益算が苦手ではなくなりますよ♪
この記事はものすごく長いです。目次をクリックして好きな場所にジャンプして下さい
売買で「もうける」仕組み
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
はじめに商売(物を売ってもうけること)の仕組みを確認します。
多くの小学生は物を売って儲けた経験が無いので、まず「もうける」仕組みを理解させると良いです。
仕入れと定価
物を売って儲けたいとき、自分で作ったり人から買ったりして売る物(商品)を用意しないといけない。これを「仕入れ」という。
仕入れたときの値段を「仕入れ値」や「原価(げんか)」という。
この仕入れ値よりも高い値段をつけて売ります。この値段を「定価」という。
そして商品が「定価」で売れた場合、仕入れ値(原価)との差額が儲け(利益)になる
例えば、誰かから100円で買った(仕入れた)品物に500円の定価をつけて、それが売れた場合の利益は500円ではなく500－100＝400円になる
★利益=売れた値段ー仕入れ値
(例)100円で仕入れた品物が定価500円で売れた
→利益は500円ではなく500－100＝400円
ためしに練習問題をどうぞ
X-1:売買の仕組み
Y[予5上7基本1(1)’][予5上7基本1(2)’]
解説
利益=売れた価格-仕入れ値=1500-350=1150円 と求められる
解説
利益=売れた価格-仕入れ値 なので 800=2000-□ という式ができる。これを逆算して
□=2000-800=1200円 と求められる
分かりましたか？
仕入→定価→売値
ただ実際に商売をすると、定価では売れない場合もあります。そのときは…
1-0:売買の仕組み(2)
「色がカッコいいから欲しいけど、ちょっと高いなあ」と迷うB君に、A君は「じゃあ半額でいいよ」と答えます。B君は「やった！ラッキー！」と喜んで買ってくれました。
A君は何円もうかりましたか？
解答
1000円で売ろうとして半額に値下げしたので500円で売ったことになります。
お店でフィギュアを買う=仕入れるのに100円かかっているので、売れた値段500-仕入れ値100=400円が利益になります
今の問題では値段が3種類でてきました。それぞれ名前がついていて、売買の問題でも使われるので覚えて下さい。
①お店で買った値段(=100円)
品物を用意する(仕入れる)のにかかった金額を「原価(げんか)」や「仕入値(しいれね)」と呼びます。
②最初につけた値段(=1000円)は「定価(ていか)」と呼びます
③値引きなどをして実際に売れた値段(=500円)を「売値(うりね)」や「売価(ばいか)」と呼びます。
このように、価格は❶原価(100)→❷定価(1000)→❸売値(500)と変わり、最初の原価と最後の売値の差(500-100)が「もうけ」＝「利益」になります。
途中の値段(定価)は利益と無関係なことに注意しましょう！
◆価格の変化
❶原価→❷定価→❸売値
◆利益
利益＝❸売値ー❶原価
(例)原価100円の品物に1000円の定価を付けて
500円に値引きして売る
→利益は500-100=400円
テストで確認してみましょう。
1:売買のしくみ
Y[予5上7(1)]
解説
原価1000→(x2.5)→定価2500→(-1000)→売値1500なので、利益は1500-1000=500円
解説
原価300→定価500→(-150円)→売値350→(-100)→新売値250
最後の売値(250)が原価(300)より低くなっていて利益はありません！
300-250=50円の損失(いわゆる「赤字」)
次は、もう少し本格的に売買計算を行いますが、その前に…
価格の決定と図
さっきは定価の決め方はテキトーで売値も「○円値下げ」と決めていましたが、実際には「増し」「引き」など割合を使って決定することが多く、受験算数の問題もほとんどそうなっています。
そこで割合を復習します。「大丈夫♪」な人はジャンプして下さい。
割合と「増し」「引き」(復習)
割合の基本知識を復習します。
割合
●割合の意味
→あるモノが別のモノの「何倍」かを表した数
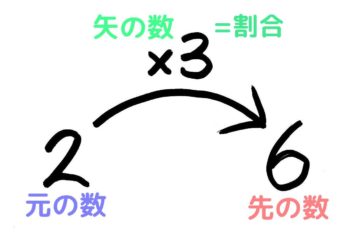
●矢印図
3つの数が「A×B=C」の関係にある時
矢印の向きに沿ってA,B,Cを並べた図
B(矢の数)が割合を示している
「2の3倍は6」
「6は２の3倍」
●矢印図による割合の公式
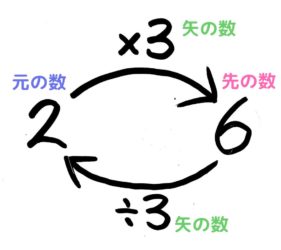
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
くわしくは姉妹サイト「そうちゃ式別館」の記事「割合の基本」を見て下さい
割合の単位
パーセントや歩合はそのままでは矢の数として計算に使えません。「～倍」という小数・分数に直します。
→あるものを100等分したうちのいくつか
「1％」→あるものを100等分したうちの一つ
「100％」→あるもの全体(×1と同じ)
●「％」を計算で使う「～倍」に直す
・「%」の分母に100をつける
「100%」→「×100100」－(約分)→「×1」
「200%」→「×200100」－(約分)→「×2」
「50%」→「×50100」－(約分)→「×12」
「50%」→「×50100」－(または)→「×0.5」
「25%」→「×25100」－(約分)→「×14」
「25%」→「×25100」－(または)→「×0.25」
「6%」→「×6100」－(約分)→「×350」
「25%」→「×25100」－(または)→「×0.06」
・「%」が小数なら分母に1000や10000を
「12.5%」→「×1251000」－(約分)→「×18」
「25%」→「×25100」－(または)→「×0.125」
歩合は％に直すようにするとラクです。
●基本ルール
1割=10%=10100=×0.1
1分＝1%=1100=×0.01
1厘＝0.1％=11000=×0.01
(例)
4厘3分2割=.420%＝20100=×0.2
4厘2割3分＝.423％＝23100＝×0.23
2割3分4厘＝23.4％＝2341000＝×0.234
増し引き
もと(100%,10割)から「増える」「減る」どちらになるかを考えるのが重要
→もとの数(100%、10割)に加える
(例)10%増し
=100%+10%=110%=もとの数×1.1
(例)3割増し
=(10割+3割=13割=もとの数×1.3
または=30％増し=130%=もとの数×1.3
(例)3割2分増し
=32%増し=(100+32)%=132%=×1.32
→もとの数(100%、10割)から引く
(例)10%引き
=100%ー10%=90%=×0.9
(例)3割引き
=10割-3割=7割=×0.7
または=30%引き=70%=×0.7
(例)3割2分引き
=32%引き=100%ー32%=68%=×0.68
くわしく復習したい人は姉妹サイト「そうちゃ式別館」の記事「割合の単位」を見て下さい。
値段の変化を計算する
以上の割合の知識を使って、値段の変化を計算します。
原価→定価
定価を決めるときは、「原価の40％増し」「4割の利益を見込んで」など割合で表現します。
・「40%増し」＝「100％＋40％」＝「140％」＝「×1.4」です
・「4割の利益を見込んで」＝「4割増し」＝「40%増し」なので、同じく＝「×1.4」です
例えば「原価が1200円の品物に50%増しの定価をつけた」場合、原価1200×1.5=定価1800になります。
「矢印図」にするとこうなります。
見込んで定価をつける
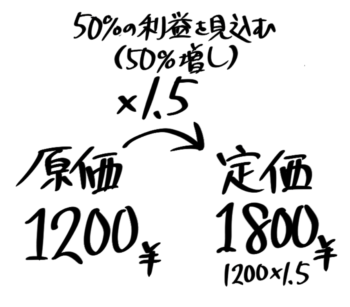
の矢印図になる
練習問題をどうぞ
X-1:定価の決定
Y[予5上7例題1′(1)(3)][予5上7基本1(3)][予5上10総合2(1)][予5上7基本1(4)][予5上7基本1(5)]
解説
「3割の利益を見込んで」→3割増し(x1.3)なので、600×1.3=780円
解説
原価x1.6=定価2560円なので、原価=定価2560÷1.6=1600円
解説
定価1260円が原価900円の何倍か求めると、1260÷900=1.4倍 なので、1.4-1=0.4=4割増し と求められる♪
分かりましたね？
定価→売値
定価の後に、売値を決めるときは「定価の25％引き」「定価の3割5分引き」などの表現を使います。
・「25％引き」＝「100％－25％」＝「75％」＝「×0.75」です
・「3割５分引き」＝「35％引き」＝「100－35」＝「65％」＝「×0.65」です
例えば、「定価1800円の品物を2割引きで売った」場合、定価1800×0.8=売値1440になります。
「矢印図」にするとこうなります。
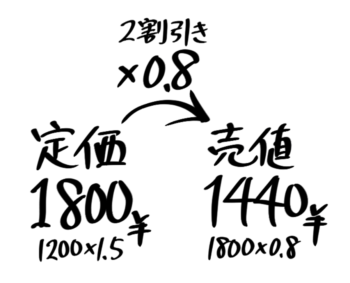
の矢印図になる
練習問題をどうぞ
X-1:売値の決定
Y[予5上7例題1′(2)(4)][予5上7基本1(6)][予5上7基本1(7)[予5上7基本1(8)][予5上10基本2(2)]
解説
2割5分引き→x(1-0.25)=x0.75 なので
売値=1600×0.75=1200円
解説
定価x0.9=売値504円 なので定価=504÷0.9=560円
解説
売値(680円)が定価(800円)の何倍かを求めると680÷800=0.85倍=85%なので、100-85=15%引きと求められる
分かったでしょうか？
原価→定価→売値
上の2つの変化をまとめると、品物を準備してから売り渡すまでの「原価→定価→売値」の変化は「二段階の矢印図」になります。
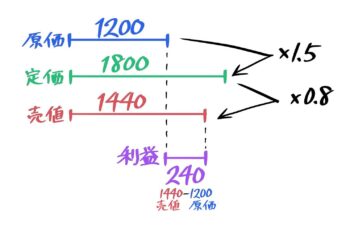
例えば「原価が1200円の品物に50%増しの定価をつけ、2割引きで売った」を矢印図にすると、こうなります。
50%増しの定価をつけ
2割引きで売った」
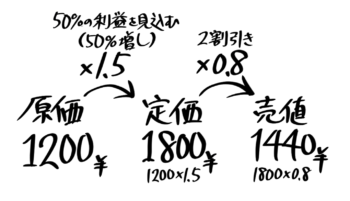
まずはこの矢印図を書ける(イメージできる)ようにして下さい
練習問題をどうぞ
X-1:原価→定価→売値
[予5上7基本1(9)]
解説
定価は400×1.5=600。売値は600×0.85=510円
解説
定価は300×1.45=435円。売値は435×0.8=348円
分かりましたね？
利益
3つの価格に加えて「利益」を書いて完成です。「利益＝原価ー売値」でしたね。
50%増しの定価をつけ
2割引きで売った時の利益
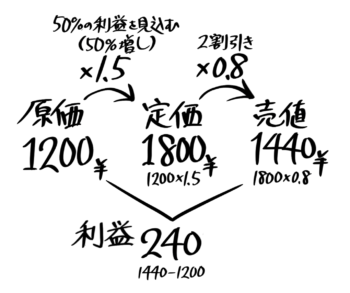
の差240が利益になります
この矢印図を書ける(イメージできる)ようにして下さい
練習問題をどぞ
X-1:利益を求める
Y[予5上7例題2′][予5上7基本1(10)][予5上10基本2(3)]
解説
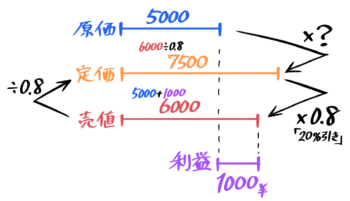
「3割の利益を見込む」＝「3割増し」=×1.3なので、定価は2000×1.3＝2600円
「15%引き」=「100-15=85%」=×0.85なので、売値は2600×0.85=2210円
利益=売値2210-原価2000=210円になる
解説
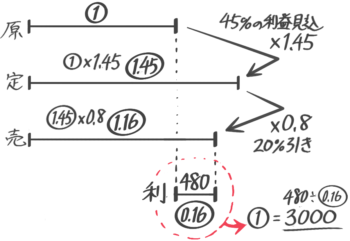
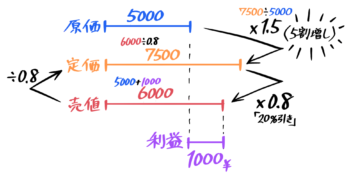
「45%の利益を見込む」＝「45%増し」=×1.45なので、定価は1500×1.45＝2175円
売値は2175-185=1990円
利益=売値1990-原価1500=490円になる
解説
「2割の利益を見込む」＝「2割増し」=×1.2なので、定価は1000×1.2＝1200円
売値は1200×0.8=960円 で原価より低いので赤字になる。
損失=原価1000-売値960=40円になる
分かりましたね？
価格決定の線分図
矢印図でも問題は解けますが、もっと直感的に簡単に解くために「線分図」にしてみましょう。
塾のテキストや参考書で「原価定価売値を1本にまとめた線分図」を見かけますが、オススメしません。
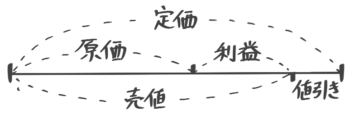
オススメしない理由は2つ
➀「まとめた」図というのは問題を読みながら上手に書くのは大変
➁価格の「移り変わり」が分かりにくい
そこで「そうちゃ式」では矢印図を素直に線分図にする方法を紹介します
書き方・解き方を理解
さっきと同じ問題を線分図で解いてみましょう
3-0:線分図の書き方
解説
上から原価、定価、売値の線分図を3段で並べ、矢印でつなぎます。
50%増しの定価をつけ
2割引きで売った」線分図
そして利益を原価と売値の差として書きます。
50%増しの定価をつけ
2割引きで売った時の利益」線分図
「売値-原価=利益」が一目で分かる。
これが売買損益算で使う「多段の線分図」です。
「矢印図」と「線分図」を並べるとこうなります。
50%増しの定価をつけ
2割引きで売った時の利益
このような「短」「長」「中」の三本と「短・中の差」の四本という「4段の線分図」が一番多く利用するパターンです。
●上から「原価」「定価」「売値」を並べる
●利益は売値と原価の差になる
(例)原価が1200円の品物に
50%増しの定価をつけ
2割引きで売った利益→240円
類題で定着
(2023.4.26作成中)
単独売買の問題
爽茶「相当還元算」と似た解き方になるので、関連記事「相当還元算の図の書き方・解き方」を見ておくと良いでしょう。
原価を求める
利益から求める
利益から原価(仕入れ値)を求めるのが基本です。
4-1-0:原価を求める
Y[予5上7例題3′][予5上10練習3(1)]
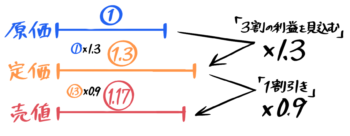
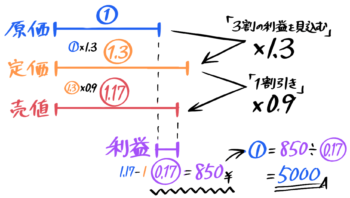
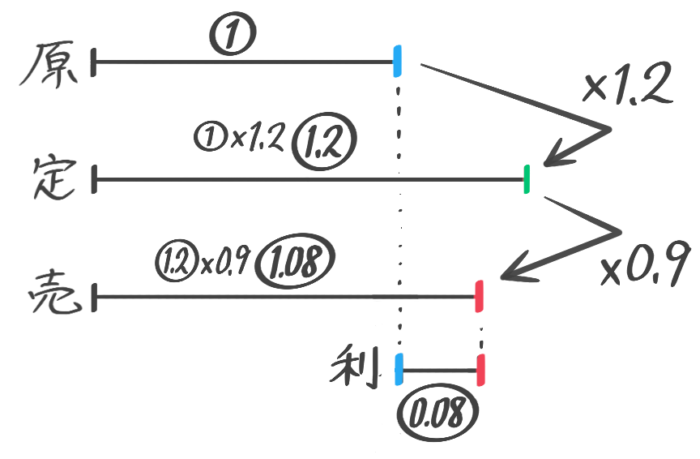
原価を➀とおくと、定価は➀×1.3=1.3に、売値は1.3×0.9=1.17になります。
よって利益は1.17-➀=0.17になり、これが850円にあたります。
0.17=850円なので、➀=850÷0.17=5000で、原価は5000円と分かりました。
練習問題をどうぞ
X-1:利益から原価を求める
Y[予5上7練習2(1)’]
ヒント
4段線分図の原価に「①」と書くところからスタート♪
解説
原価を①とすると、売値は①x1.45×0.8=1.16になる。
利益は0.16=480円なので、①=480÷0.16=3000円と求められます
損失から求める
利益でなく、損失が出る場合もあります
損失からの定価推定
(1)仕入れ値は何円か(2)定価は何円か
[予5上7練習2(2)改造]
(問題文省略。テキストを見て下さい)
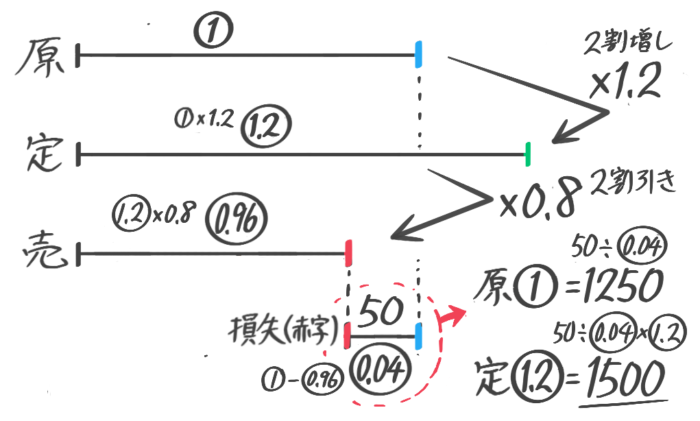
線分図を書くと損失0.04=50と分かる
定価は50÷0.04×1.2=1500円と求められる(原価①=1250円と出してからx1.2しても良い)
練習問題をどうぞ
分かりましたか？
定価と利益から原価を求める
仕入れた品物に 円の定価をつけ、20%引きで売ったところ利益が 円になった。以下の問いに答えなさい
[予5上10基本3]
(1)何円で売れたか
(2)仕入れ値は何円か
「利益の差」から原価を求める
(問題文省略。テキストを見て下さい)
[予5上7練習1(1)]
問題を読みながら、いつもの四段線分図を書く
この問題では利益そのものでなく「定価で売れた場合の利益との差」が180円だというので、それを5段目として書いてみる
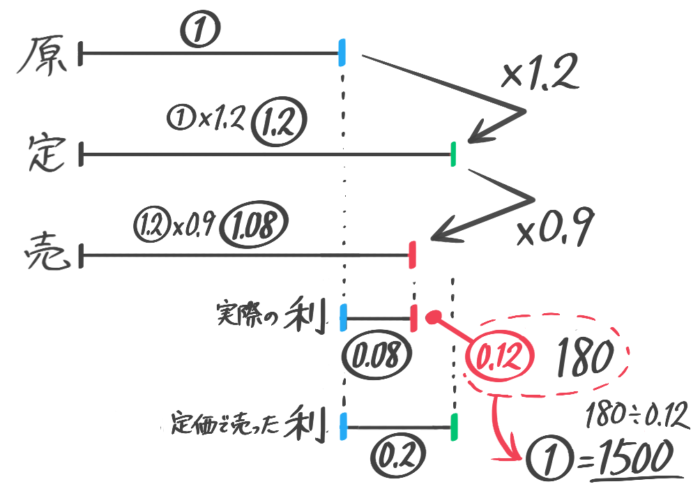
「定価で売れた場合の利益との差」は0.12=180円 なので①=1500円と求められる
定価(の割合)を求める
原価と利益から、定価(の割合=定価の付け方)を求める問題。まずは図を書いてみること。
4-2-0:定価(の割合)を求める
Y[予5上基本問題2]
解説
まず書けるだけの線分図を書いてみる
図を見ると、
(1)売値=原価5000+利益1000=6000円。と分かる。
(2)さらに矢印を逆にすると定価=売値6000÷0.8=7500円と分かる♪
定価は売値÷0.8=7500と分かる
(3)原価から定価への割合(矢の数)は7500(先の数)÷5000(元の数)=1.5と求められる。
「5割増し」と分かる
×1.5なので「5割増し」の定価をつけたと分かりました
練習問題(2023年度中に補充予定)
売値(値引き)の割合を求める
原価・定価と利益から、何割引きの売値をつけたのか求める
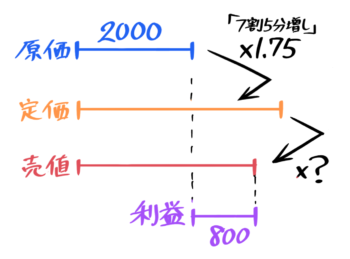
4-3-0:値引きの割合を求める
解説
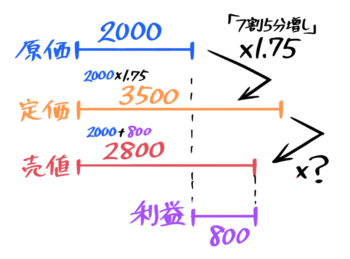
まずは書けるだけの図を書く。
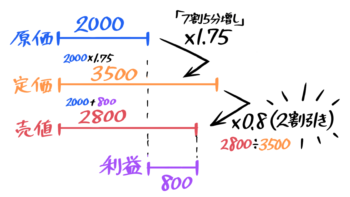
問題文から定価は2000×1.75=3500円。売値は2000+800=2800円と求められる。
?=2800÷3500=0.8なので、売値は定価の8割=2割引きしたと分かる。
定価の2割引きと分かる♪
確認テスト(2021.8.14作成中)
足し算引き算まじりの問題
割合(かけ算)だけでなく足し算引き算がまじった問題は少し難しくなります。パッと分からない場合、すぐに図を書きましょう。
値引きが引き算
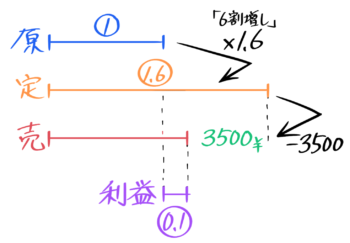
4-4-0:引き算まじりの問題
解説
とりあえず、問題文の数値を図にします
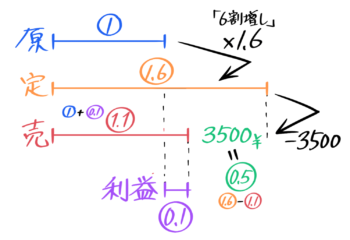
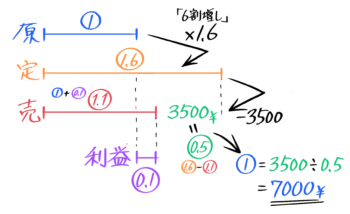
売値は原価➀+利益0.1=1.1になり、定価1.6との差=0.5が3500です。
「3500=0.5」なので、原価➀=3500÷0.5=7000円と分かります♪
定価が足し算
さらに損失なので少し面倒な問題
X-1:損失から原価を求める
Y[予5上7練習1(2)]
ヒント
線分図の長さがいつもの「短,長,中」と違うのに注意！
解説
線分図を書きます。「損失」が出ているので売値が原価より短くなります。
線分の長さがいつもは上から「短い,長い,中くらい」だったのが、ここでは「中くらい,長い,短い」となります
売値を0.6と480円に分けて480円を損失160円とくっつけると0.4=640円と分かります。
これで①=640÷0.4=1600円と求められます
2種類の売値
両方黒字
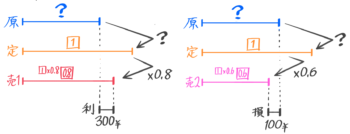
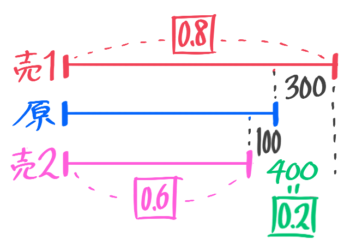
2種類の売値から定価①と原価を求める問題
4-5-0:2種類の売値
[予5上10基本5]
ヒント
ずっと原価を➀としてきましたが…
解説
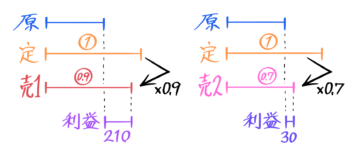
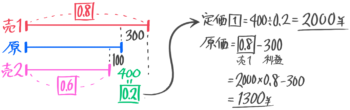
定価の決め方が書いていないので、原価ではなく定価を➀として図を書きます。売値が2種類あるので、ここでは2つの図を書きます(テストの時は丸数字だけでも良い)
原価と売値10.9の差が利益210円、原価と売値20.7の差が利益30円になっています。
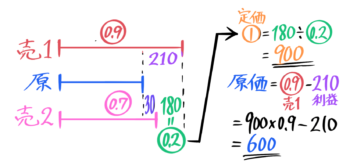
これだけでは良く分からないので、「売値1」「原価」「売値2」を並べた線分図を書きます。
線分図の問題になる
差に注目すると「0.2=180円」と気づきます(よね？)
これで定価➀=180÷0.2=900円と分かります。さらに「売値1」=900×0.9=810と出して、売値810-利益210=原価600円と求められました。
練習問題
片方赤字
一方が赤字になる場合もどうぞ
X-1:2種類の定価
Y[予5上7例題4′][予5上7基本3]
ヒント
ここでも定価を1としましょう
解説
原価も定価への増しの割合も分からないので定価を1として線分図を書くとこうなる
これを見ても解答への道筋が思いつかないなら、定価・売値1・売値2を並べてみる
すると、売値10.8と売値10.6の差0.2が100+300=400と等しいと分かる。あとはいつものやり方で定価を400÷0.2=2000円と出して…
売値10.8=2000×0.8=1600円から300円引けば(または売値20.6=2000×0.6=1200円に100円足せば)原価が1300円と出る
練習問題(2023.4.26作成中)
複数個売買の仕組み
爽茶これまでは一個の品物しか考えませんでした(単数売買)が、ここからは沢山の品物を販売する場合(複数売買)について考えます。
売上高と利益
はじめに、簡単な例題で複数売買の基本を理解して下さい♪
5-1:複数個販売(定価完売)
Y[予5上7例題5補完1]
解説
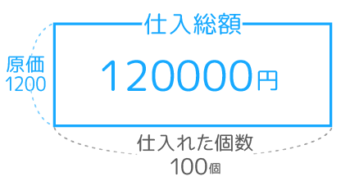
商品を仕入れるのにかかる費用は1200×100=120000円で、これを「仕入総額(しいれそうがく)」という
=商品全部を仕入れるのにかかった費用
●仕入総額=原価 x 仕入れ個数
(例)1200円の品物を100個仕入れる
→1200 x 100 =12000円
そして、定価は「5割増し」=x1.5 なので 1200×1.5=1800円
(二段の線分図)
この1800円の商品100個が完売したので、お客さんから受け取ってレジに入っている金額は1800 x 100 =180000円。これを「売上高(うりあげだか)」という
=商品と引き換えに客から受け取った金額
売上高=実際の売値 x 販売個数
(例)1800円の品物が100個売れた
→売上高は 1800×100=180000円
では、A商店の「もうけ=利益」はいくらでしょうか？
当然ですが、レジに入っている売上高180000円全部が利益ではありません。
売上高180000から商品の仕入れにかかった仕入総額120000を引いた 180000–120000=60000円が利益になります。
このように複数売買の利益は「売上高」ー「仕入総額」で求めます。
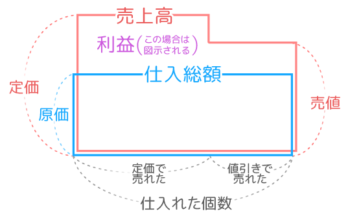
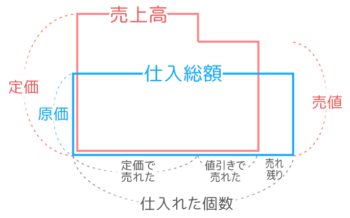
複数個の売買の仕組みと用語をまとめるとこうなります。
◇仕入総額=原価 x 仕入れ個数
◇売上高=実際の売値 x 売上個数
◆利益=売上高ー仕入総額
＝(実際の売値 x 売上個数)ー(原価 x 仕入れ個数)
(例)1200円の品物を100個仕入れ、5割増しの定価を付けて完売した
→定価は1200×1.5=1800円
→利益は (1800×100)-(1200×100)=60000
これは単純な問題でしたが、テストではもう少し複雑な問題を解くので、解き方に工夫が必要になります。
それが「面積図」です！
線分図から面積図へ
定価完売の面積図
さっきの例題を使って面積図を書いてみましょう
5-2-1:定価完売
Y[予5上7例題5補完1]
まず仕入総額を、「仕入総額=原価 x 仕入個数」の関係を使って長方形の面積図にします。
面積が仕入総額になる
縦1200×横100=面積120000の長方形になりました。
次に売上高を「売上高=実際の売値 x 売上個数」の関係を使って面積図にします。
この問題では実際の売値=定価になっていて、定価は原価1200円x1.5=1800円です(単数売買の考え方と同じですが、線分図が縦になっている)
これを縦の長さにして売上高の面積図を書くとこうなる
面積が売上高になる
そして、2つの面積図を下をそろえて重ねます
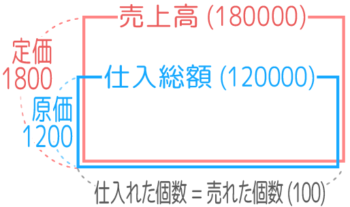
これで「定価で全部売れた(定価完売)場合」の面積図が完成しました。
利益=売上高(180000)-仕入総額(120000)=60000円です。
注意点
この「定価完売」の場合は売上高の中に仕入総額がすっぽり収まっているので利益が図に示されています(紫色の部分)
よって「利益=売上高ー仕入総額」という計算だけでなく、「商品1個あたりの利益(1800-1200)x売れた個数(100)=60000」という計算でも利益を出すことができます。
ただ、これは特別な(ラッキーな)場合であって、できない場合の方が多いです
この一番単純なパターンを「定価完売」と名付けます。
この「定価完売」で終わればハッピーなのですが…
売れ残りがある場合
実際には「定価完売」するとは限りません。例えば、こんな場合です。
5-2-2:定価売れ残り
Y[予5上7例題6補完]
解説
定価では全部が売れなかった場合です。「定価売れ残り」と名付けます
仕入総額は変わらず1200×100=120000で、面積図も同じ
一方、売上高は売れた個数1800×90=162000に減ってしまいました。
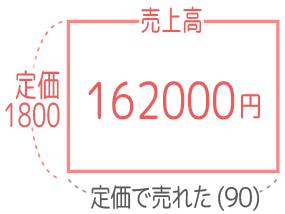
面積図を重ねるとこうなります
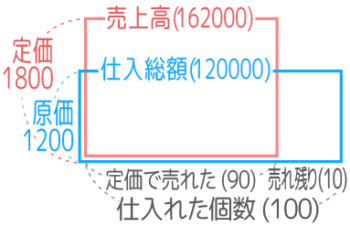
公式「利益=売上高-仕入総額」より、利益は162000-120000=42000円と分かります。
利益は公式で出す
さて、この例題「定価売れ残り」は、はじめの例題「定価完売」と違って、利益が図示されません
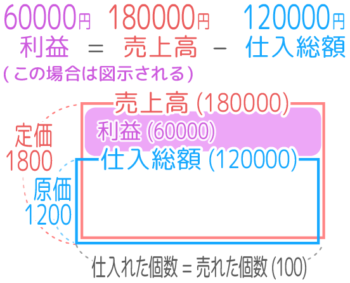
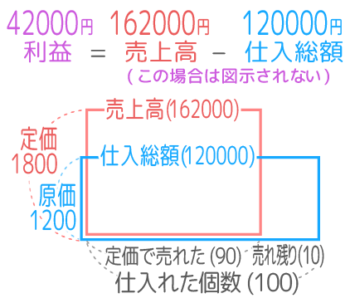
したがって、図とは別に公式「利益=売上高-仕入総額」を使わないと答えを出すのは難しいです。
入試では、このような「利益が面積図に図示されない場合」が出題されることも多いので、複数売買の利益は公式を使って出すのことも覚えておきましょう。
→面積図には表れないことがある
(図形的に面積として求められない)
→その場合は公式「利益=売上高ー仕入総額」
を使って求める
複数売買の仕組みと公式の基本は以上です。
この後は「定価完売」「定価売れ残り」以外を含めた、色々なパターンを解いていきましょう♪
色々な複数売買のパターン
ここからは、複数売買の色々なパターンと解き方を見ていきましょう
全てに共通するのは「利益=売上高ー仕入総額」の公式
◇仕入総額=原価 x 仕入れ個数
◇売上高=実際の売値 x 売上個数
◆利益=売上高ー仕入総額
＝(実際の売値 x 売上個数)ー(原価 x 仕入れ個数)
また、仕入総額は単純な長方形になるのが普通ですが、
売上高は色々な形になります。
((定価完売、定価売れ残り、値引き完売、値引き売れ残りの図一覧))
それでは、単純なパターンから複雑なパターンへ、順番に見ていきます
定価完売
(上で見たように)全部の品物が定価で売れた場合で、仕入総額と売上高は幅は等しく高さが異なる2つの長方形として確認できます
(等しい幅の2つの長方形)
代表的な問題を解いてみましょう
定価を求める
利益から定価(の割合)を求める問題です
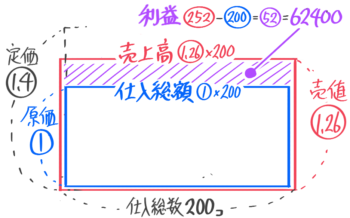
X-1:定価完売(1)
解説
仕入総額=原価(200)x仕入総数(100)=20000円、利益が8000円なので、売上高=20000+8000=28000円と分かる
売上高=実際の売値x売上個数で、ここでは売値=定価なので、売上高28000=定価x100 より定価=28000÷100=280円
定価280円が原価200円の何倍か求めると280÷200=1.4倍なので、定価は原価の4割増しと分かる
確認問題
(2023.10.31作成中)
原価を求める
利益から原価①を求める問題です。
X-1:定価完売(2)
解説
原価が分からないので1とすると、定価は1x1.4=1.4、売値は1.4x0.9=1.26になる。
この丸数字を使うと、仕入総額=原価x仕入個数=1x200=200、売上高=売値x売上数=1.26x200=252で、利益=売上高-仕入総額=252–200=52=62400円と分かる
「52=62400」なので、原価1=62400÷52=1200円
割合だけの問題
仕入総額に対する割合で利益を指定された場合の定価(売値)(の割合)を求める
X-1:定価完売(3)
ヒント
定価も仕入れ値も金額が書いてないので1とおきましょう
解説
定価を①、仕入総数を1とすると、仕入総額=①x1=1で、利益は1x0.7=0.7 、売上高は1+0.7=1.7です。
定価(売値)=売上高1.7÷仕入総数1=1.7
なので、定価は原価の7割増しです
(定価完売では割増分がそのまま利益になります。面積図を考えると分かります。)
「定価完売」のパターンは以上です。
定価売れ残り
定価でのみ販売し売れ残った時点で終了したパターン(壊れた腐った等の理由で捨ててしまう)で、利益は図に表れない
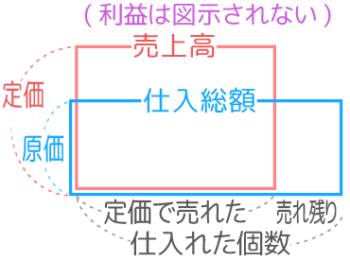
利益を計算する
前述(例題5-2-2)参照
定価と割合を求める
仕入れと利益から売値を求める問題
原価を求める
原価①を求める問題
(2023.10.31作成中)
仕入れた個数を求める
仕入れた個数が分からない問題です
1-1:サブタイトル
仕入れた個数が分からないので仕入れ総額も分からず、単純には計算できません。
そこで面積図を使った工夫をします。
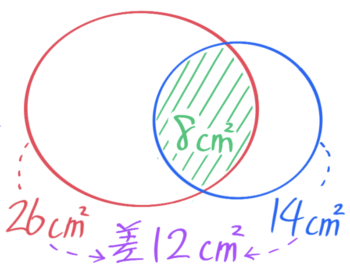
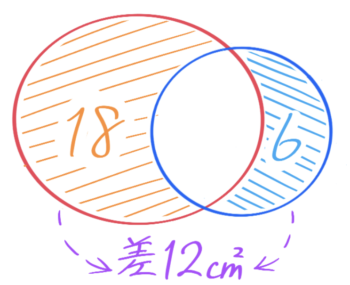
「はみ出し部分」の関係
利益の公式「利益＝売上高－仕入総額」を面積図で考えると、赤い長方形の面積と青い長方形の面積の差が利益ということ
そして2つの図形が重なっている場合、重なっている図形の差とはみ出ている2つの部分の差と等しくなります(関連記事「面積図の学び方」から簡単な例を示します)
他の単元でも使うので覚えておきましょう
これを「定価売れ残り」の面積図にも適用すると…
上にはみ出た部分と横にはみ出た部分の差は利益と等しくなります。
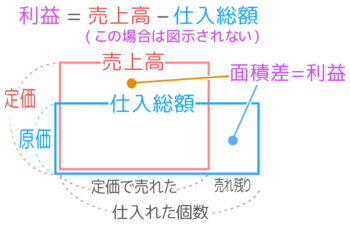
これを使って、先程の問題を解きます。
X-1:定価売れ残り
[予5上7例題6′]
ヒント
上にある「はみ出た部分の差が利益と等しい」を使いましょ
解説
問題を読みながら定価を求めて(50×1.8=90円)、面積図を書くとこうなる
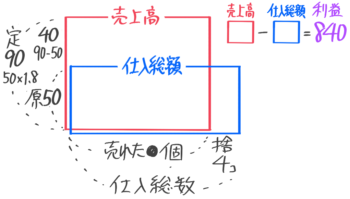
売上高(赤い長方形)と仕入総額(青い長方形)の面積の差が利益(840)と等しい(図からは分からない。問題文で分かる)
ここで「はみ出た部分の差は利益と等しい」ことを利用すると
上にはみ出た部分(A)と横にはみ出た部分(B)の面積の差も利益と等しいので
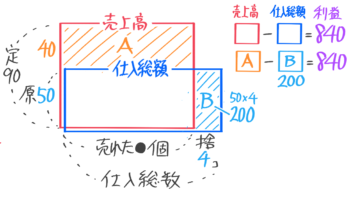
Aの面積=Bの面積(4×50=200)+840=1040と分かる。
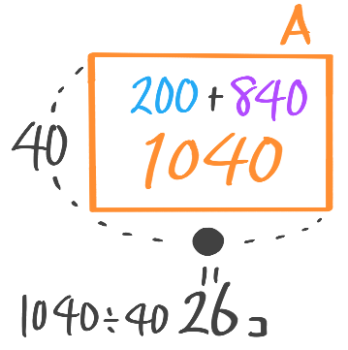
そしてAの縦の長さは40なので横の長さ(●=売れた個数)は1040÷40=26個、仕入れた個数は26+4=30個と求められる
練習問題
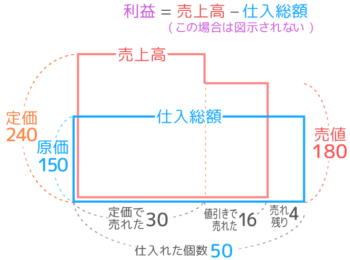
ある品物を何個か仕入れて○割の利益を見込んで1個●円の定価をつけて販売したが、⦿個が壊れていて売れず捨てざるをえなかった。利益が2680円のとき、仕入れた個数を求めよ
Y[予5上7練習3]
面積図はこう
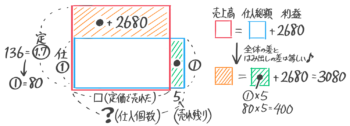
注目点は
・原価を①とすると定価1.7=136円より①=80と出せること
・利益が2680円→売上高と仕入れ総額の差が2680円なので、はみ出た部分の差も2680円になる
です。
そして右にはみ出た緑の面積が400なので上にはみ出たオレンジの面積は3080と分かります。
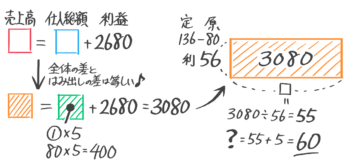
オレンジの縦は56なので横(□=定価で売れた個数)は55個、仕入れた数は全部で55+5=60個と求められます
「定価売れ残り」パターンは以上です。
値引き完売
定価では全部が売れなかったが、売れ残ったものを値引きをしたら残りが全部売れた場合(ホッ)です。
利益は「つるかめ算」の面積図のようなL字形で図示される
「つるかめ算」の一種として多く出題されるパターンです。(つるかめ算を忘れた人は関連記事「つるかめ算まとめ」を見ておいて下さい)
利益を求める練習
「値引き完売」パターンに慣れるために、利益計算の練習をしてみましょう
6-3-1:値引き完売の利益
Y[予5上7基本4][予5上10基本4]
解説
まず「原価→定価→値引きした売値」と変化する3つの価格を確認します
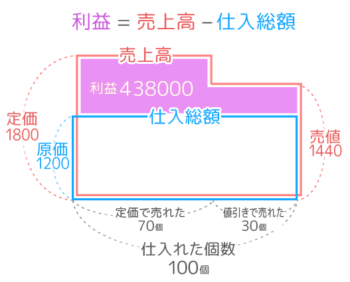
原価1200→(x1.5)→定価1800円→(x0.8)→売値1440円です
(線分図)
この価格で「利益=売上高ー仕入総額」の公式を使います
仕入総額は原価1200×100=120000円で、「定価完売」「定価売れ残り」の場合と同じ
一方、売上高は単純な長方形ではなく、2つの長方形が合わさった形になります。
まず定価1800円で70個が売れた部分は1800×70＝126000円、値引きした売値1440円で30個が売れた部分は1440×30＝43200円で、合計の売上高は558000円です。
以上より、売上高558000–仕入総額120000=438000円が利益です
「値引き完売」パターンでは仕入総額が売上高の中に収まっているので、利益が図示されます
売上高と仕入総額のスキマの紫のL字形が利益を表しています。
練習問題(作成中)
「値引き完売」の仕組みが分かったところで、問題を解いてみましょう
(値引きした)売値と割合を求める
値引きした個数を求める
つるかめ算の問題になる
X-1:値引き完売
Y[予5上7例題7′]
ヒント
つるかめ算の形を見つけましょう
解説
まず定価と値引きした売価をだしておくと、定価=150×1.4=210円、売価=210×0.9=189円。
また仕入総額は150×40=6000円、利益が2148円なので売上高は6000+2148=8148円。
仕入れ総数40個と売れ残り？個として面積図を書くとこうなる
本問のような「値引き完売」パターンでは、上にはみ出た部分(紫)が利益そのものなので、この部分を面積2148のL字形とみて、つるかめ算を解くと…
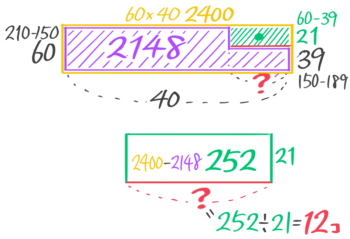
？=12個と分かりました。
また、売上高全体も面積8148のL字形になっているので、計算が少し面倒ですが、こちらで解いても良いでしょう(本当は、こちらの解き方が基本になります)。
練習(作成中)
異なった利益表現
ある品物を●個仕入れて⦿%の利益を見込んで定価をつけて販売したところ何個か売れ残ってしまった。そこで翌日売れ残りを定価を1割引きで販売したところ完売した。利益は○円で、これは仕入れた分が全て定価で売れた場合の利益の6割にあたる。以下の問いに答えなさい
Y[予5上7練習6]
(1)全て定価で売れた場合の利益は何円か
(2)1個の仕入れ値は何円か
(3)2日目に売れたのは何個か
値引きして完売した実際の面積図と「全部定価で売れた」面積図を並べてみる
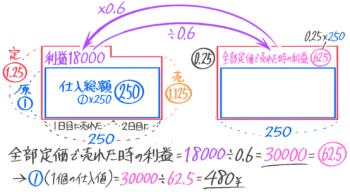
全部売れた時の利益は18000÷0.6=30000円。これは1個あたりの利益0.25×250個=62.5と等しいので、原価①=30000÷62.5=480円と求められる。
次に実際の面積図の利益部分のL字形でつるかめ算を解くと
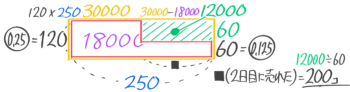
2日目に売れた数(■)=200個と求められる
答 (1)30000円 (2)480円 (3)200個
二回値引きをした場合
売上高の面積が三段になり、三量のつるかめ算の問題になる(面倒くさい！)
「値引き完売」パターンは以上です
値引き売れ残り
値引きをしても結局、全部は売れず、売れ残ったものは捨てた場合(消費期限がある食品を売る場合はありがち)。
利益は図示されませんが、はみ出た部分の差が利益になるのを利用できます。
利益を出す練習
利益=売上高(赤いL字形)-仕入総額(青い長方形)です
練習してみましょう
X-1:値引き売れ残り
Y[予5上7例題5′]
ヒント
上の面積図をイメージして計算しましょ
解説
価格を計算してしまうと、原価150円、定価150×1.6=240円、値引きした売値=240×0.75=180円。
個数は、定価で売れたのが30個、最後まで売れ残った(捨てた)のが4個、値引きで売れたのが50-30-4=16個。
これらを面積図にすると、こうなります(この問題ではイメージするだけでもよい)。
売上高は(240×30:定価で売れた分)+(180×16:値引きで売れた分)=7200+2880=10080円、仕入総額は150×50=7500円。
よって利益は10080-7500=2580円と求められます
分かりましたか？
練習問題(2013年度中に補充予定)
個数を求める
つるかめ無し
ある品物を1個○円で⦿個仕入れて3割5分の利益を見込んで定価をつけ販売したところ●個売れ残った。それらを2日目に◎円値引きして販売したがまたいくつか売れ残り、それらは捨てた。全体の利益が◆円のとき以下の問いに答えよ
[予5上7練習4]
問題文を面積図にしていきます。仕入れ個数100,原価300なので仕入総額は30000。定価は405円,値引きした後の売値は315円,定価で売れたのは76個
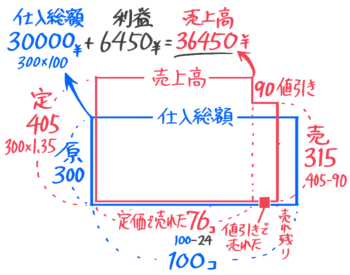
ここで、仕入総額+利益=売上高なので売上高30000+6450=36450円と分かります。
次に売上高のL字形に注目すると…
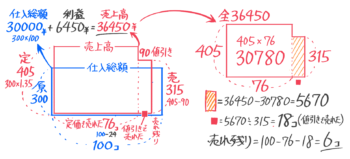
全売上高36450円から定価での売上30780円を引いた5670円が値引きでの売上(オレンジ)なので値引きで売れた個数は18個、売れ残った残ったのは100-76-18=6個と求められました
答 (1)36450円 (2)6個
つるかめあり
こんな問題です
X-1:値引き売れ残り
[予5上7練習5′][予5上10練習3(2)]
ヒント
売上高の面積を図形的でない方法で求めれば、つるかめ算にできる
解説
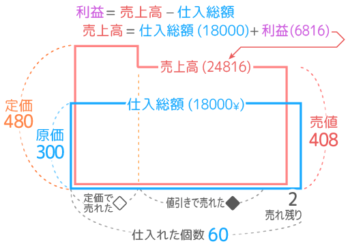
問題文を読みながら面積図を書く。
仕入総額は原価300円x仕入個数60個の長方形(青)に、売上高は定価480円、値引きした売値408円を左右の高さに持つ幅60-2=58のL字形(赤)になる。
売上高の面積は図形的には求められないが、利益が6816円なので、仕入総額18000+利益6816=24816円と分かる。
この売上高のL字形が鶴亀算の面積図になっている
L字形を包む長方形(黄)の面積278400からL字形(赤)の面積26700を引いた「欠け」の面積は3024なので、その横幅(◆=値引きで売れた個数)は3024÷72=42個、定価で売れた個数(◇)は58-42=16個と求められます
値引きを二回以上した場合
三段になります
「三量のつるかめ」になります。「三量のつるかめ」には、結局二量にできる「偽の～」と、いもづる算を使う面倒くさい「真の～」があります。
例題(偽の三量つるかめ)
例題(真の三量つるかめ)
「値引き売れ残り」パターンは以上です
捨て値完売
値引きしても売れ残るので、最後は原価よりも安い「捨て値」で全部売り切った場合
この場合も利益は図示されない
利益を出す練習
捨て値で売った個数
捨て値を求める
「捨て値売れ残り」パターンは以上です
その他のパターン
複数売買は以上です
その他の売買の問題
オススメ教材
爽茶●「売買」だけを解きたい場合は「思考力算数練習帳シリーズ」の「売買算」(サイパー算数)
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題」シリーズ(日能研)
●小6受験生には「算数ベストチェック」(日能研)
「分かりやすい！」と評判の
今なら14日間無料。興味がある人は「先取りや予習・復習に！ スタディサプリ そうちゃ式のオススメ利用法」へ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!