割合が難しい!比がわからない!」というのは中学受験の5年生でよく聞く悩みです。
基本の考え方をイメージとともに理解・記憶して、応用するようにすれば大丈夫
この記事では東大卒講師歴20年の図解講師「そうちゃ」が「割合・比」の内容を総まとめします。
記事をながめて「ここ分からないな」苦手だな」と思ったら、個別の記事に飛んで詳しい解説を読んだりや問題を解くと良いでしょう。
この記事を最後まで「ふんふん、そうだよね」と読めたなら、基本は大丈夫です
割合の基本事項
受験算数の割合の問題はいろんな種類がありますが、基本になる「割合の考え方」は共通しています。
この考え方を理解し、図に出来るようにしてから先にすすみましょう。
割合の意味
ズバリ「割合=かけ算」です。それ以上の詳しい説明は要りません。
大事なのは、3つの数量の関係をイメージにすることです。
→あるモノが別のモノの「何倍」かを表した数
●矢印図
3つの数が「A×B=C」の関係にある時
矢印の向きに沿ってA,B,Cを並べた図
B(矢の数)が割合を示している
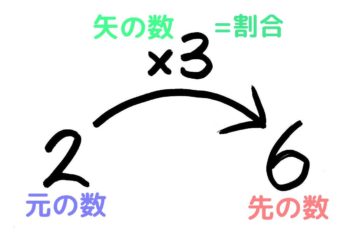
「2の3倍は6」
「6は2の3倍」

●矢印図による割合の公式
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
詳しくは、姉妹サイト「そうちゃ式別館」の「割合の考え方」「割合の文章問題」を見て下さい。
割合の単位
割合には独特の単位を使うので、これらに馴染んでおきます
%と歩合
パーセントや歩合はそのままでは矢の数として計算に使えません。「~倍」という小数・分数に直します。
これを理解記憶して、パッと使いこなせないと問題は解けません
→あるものを100等分したうちのいくつか
「1%」→あるものを100等分したうちの一つ
「100%」→あるもの全体(×1と同じ)
●「%」の分母に100をつける
「100%」→「×100100」-(約分)→「×1」
「200%」→「×200100」-(約分)→「×2」
「50%」→「×50100」-(約分)→「×12」
「50%」→「×50100」-(または)→「×0.5」
「25%」→「×25100」-(約分)→「×14」
「25%」→「×25100」-(または)→「×0.25」
「6%」→「×6100」-(約分)→「×350」
「25%」→「×25100」-(または)→「×0.06」
●「%」が小数なら分母に1000や10000を
「12.5%」→「×1251000」-(約分)→「×18」
「25%」→「×25100」-(または)→「×0.125」
歩合は%に直すようにするとラクです。
●基本ルール
1割=10%=10100=×0.1
1分=1%=1100=×0.01
1厘=0.1%=101000=×0.01
(例)
4厘3分2割=.420%=20100=×0.2
4厘2割3分=.423%=23100=×0.23
2割3分4厘=23.4%=2341000=×0.234
「増し」と「引き」
売買計算で多く使います。コツはもと(100%,10割)から増えるか減るかを考えることです。
→もとの数(100%、10割)に加える
(例)10%増し
=100%+10%=110%=もとの数×1.1
(例)3割増し
=(10割+3割=13割=もとの数×1.3
または=30%増し=130%=もとの数×1.3
(例)3割2分増し
=32%増し=(100+32)%=132%=×1.32
→もとの数(100%、10割)から引く
(例)10%引き
=100%ー10%=90%=×0.9
(例)3割引き
=10割-3割=7割=×0.7
または=30%引き=70%=×0.7
(例)3割2分引き
=32%引き=100%ー32%=68%=×0.68
くわしく復習したい人は姉妹サイト「そうちゃ式別館」の記事「割合の単位」を見て下さい。
割合の応用1~相当還元算
矢印図を一本の線分図に直します。
くわしくは関連記事「相当還元算」を見て下さい
割合の応用2~売買
大きく2つのパートから出来ている内容が大きい単元です。
単独売買の問題
売買の前半は、1個の品物を売る「単独売買」の問題です。
原価→定価→売値と変化する価格を3(+1)本の線分図にして解きます。
2割引きで売った時の利益」を図にする
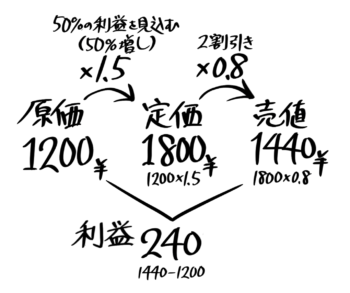
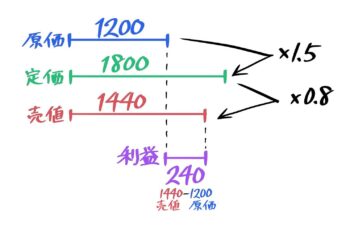
線分図に直したあとは、相当還元算と同じ解き方になります。
複数売買の問題
売買の後半は、品物を多数仕入れて販売する「複数売買」の問題です。
面積図にすると理解しやすいでしょう。
面積図にした後はつるかめ算を利用したりして解きますが、利益を完全には図示できないのが難しく感じられます。
詳しくは関連記事「売買損益算」を見て下さい
割合の応用3~濃度
矢印図をビーカー図にする
詳しくは関連記事「濃度計算」を見て下さい
比の基本
くわしくは関連記事「比の基本」を見て下さい
比の応用~倍数算
和と差で学んだ「分配算」にも軽く比が出てきましたが、二種類の比の操作がメインになるのが「比例倍数算」です。
比と割合の応用~仕事算
単位あたりの量(平均)の考え方の延長ですが、比を使うことがあるのでコチラでも紹介
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ