中学受験生で「比が苦手！」という人もいるかもしれません。
確かに比の利用問題(図形と比、速さと比)は難しいのですが、比そのものには簡単な問題も多いんですよ。
まずは簡単な問題を完全に定着させて、難しい問題に少しづつ挑戦しましょう。
この記事では東大卒講師歴20年の図解講師「そうちゃ」が比の基本から文章題までを超分かりやすく説明します。
記事を読んで真似すれば「比」が好き得意になるでしょう♪
この記事は非常に長いです。目次をクリックすると好きな箇所にジャンプできます。
比の基礎
「比」とは、単純に言うと、2つの数の関係を表したものです。
比の形
「比」のかたちを示します。
これはAの大きさを1とするとBの大きさが2ということを表します。線分図にすると次のようになります。
小数・分数の比
また、比を作る数は整数だけでなく小数や分数でもOKです。
ただ、テストの答えとして小数や分数の比を書くとバツになる(仮分数のような扱い)ので、このあと説明する「比の単純化」を行います。
3つの数の比
また、3つ以上の数を比にすることもあります。
これはAの大きさを1とするとBの大きさが2ということを表します。線分図にすると次のようになります。
比の値
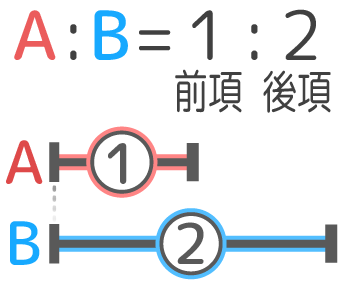
前項・後項
2つの数の比の左の数を前項、右の数を後項と呼びます(図1)
比の値
前項÷後項=前後を「比の値」と呼びます。
例えば、A:B=1:2 の時、比の値は前(1)÷後ろ(2)=12 になります。
これは、AはBの12ということを意味しています。
分かりましたね？確認テストをどうぞ
1-1:比の値
解説
前(3)÷後(8)=38
ヒント
小数の比でも「前」÷「後」です♪
解説
前(1.2)÷後(0.3)=1.20.3=(分子分母を10倍)=123=4
ヒント
分数でも「前」÷「後」♪
解説
前(73)÷後(711)=7 x 113 x 7=113=323
分かりましたか？
この「比の値」そのものは入試で聞かれることも(ほとんど)ありませんが、「比は分数と同じようなもの」という感覚がものすごく大切です
逆比
2数の逆比
比「A:B」を「B:A」とするように、比の前項と後項を入れ替えたものを「逆比」と呼ぶ
例えば「2:3」の逆比は「3：2」になる
3数の逆比
「1:2:3」のような3数の場合は、前後を入れ替えて逆比を作れません(「3:2:1」ではありません)
実は、3数の場合に限らず、それぞれを数(項)を逆数にすると逆比になります(詳しい説明は後で)。
「1:2:3」の場合、「11:12:13」が逆比になります。
ただ、このままだと答えとしてはバツなので、この後説明する「単純化」で整数に直します。
比の単純化
比の基本操作
比のそれぞれの数(項)に同じ数をかけたり割ったりしても比は等しいままです
例えば「1:2」という比に、2をかけて、３をかけて、６で割る、としてみます。
x2↓ ↓x2
2:4
x3↓ ↓x3
6 :12
÷6↓ ↓÷6
1:2
自由に行うことができる
この「1:2」「2:4」「6:12」は、全て前項が後項の12(比の値)になっています。つまりすべて等しい比です。
1:2=2:4
分数12、24、612が全て等しいのと似ていて、比もいろんな表現が可能なのです。
ただ、分数を答えに書くときは約分しないとバツになったように、比を答えに書く場合にも、一番簡単な「1:2」という比を書かないとバツになるので注意して下さい
→両方の項に同じ数をかける・割る
をしても比は等しいまま
(例1)1:2→(両方を2倍)→2:4
(例2)2:4→(両方を3倍)→6:12
(例3)6:12→(両方を÷6)→1:2
●注意！
テストの答えとしては
一番簡単な「1:2」以外はバツになる。
この「比の操作」を利用して、比をできるだけ簡単な整数にすることを当サイトでは「比の単純化」と呼びます。
実際に「比の単純化」を試してみましょう。
整数の比を単純化
「分数の約分と同じ」と考えるとラクチンです。
1-0:整数比の単純化
ヒント
1220を約分するつもりで両方を公約数で割っていく
解説
12:20→(両方を÷2)→6:10→(両方を÷2)→3:5
または最大公約数一発で割っても良い
12:20→(両方を÷4)→3:5
この時、直す前と後の比を並べると4つのうち内側の2つの積と外側の2つの積は常に等しくなっている(後で重要です)
外項
内項
内項
外項
外項の積12×5=60が
等しくなっている
小数の比を単純化
まず整数に直すのがコツです
1-2:小数比の単純化
解説
1.4:2.1→(両方を10倍)→14:21→(両方を÷7)→2:3
解説
1.25:0.75→(両方を100倍)→125:75→(両方を÷25)→5:3
分数の比を単純化
やり方が2つありますが、通分する方を好む小学生が多いです
1-3:分数比の単純化
解説
通分して分子だけを単純な比にする
45:23→(分母15に通分)→1215:1015→(分子だけを並べて比にする)→12:10→(両方÷2)→6:5
別解
分母の数字「5」「3」の最小公倍数が15なので、両方を15倍すると分母が消える
45:23を→(両方×15 4×155:×2×153)→12:10→(両方÷2)→6:5
解説
両方とも仮分数にしてから通分します
3:115→(仮分数に)→31:65→(5に通分)→155:65→(分子だけ取り出す)→15:6→(両方÷3)→5：2
整数/小数/分数混合比を単純化
全部分数にそろえてから単純化します。
1-4:小数分数混合
解説
0.4：116→(仮分数に)→25:76→(30に通分)→1230:3530→(分子だけ取り出す)→12:35
解説
114：0.6：2→(仮分数に)→54:35:21→(20に通分)→2520:1220:4020→(分子だけ取り出す)→25:12:40
比の単純化をまとめると…
＝もっとも簡単な整数比に直すこと
●整数比の単純化
→公約数で割っていく
●小数比の単純化
→まず10倍・100倍して整数比に直し
それから公約数で割っていく
●分数比の単純化
→通分して分子だけを並べて
公約数で割っていく
このような比の基礎問題をもっと解きたい人は下にある「オススメ教材」を見て下さい
逆比の作成と単純化
逆比の作り方(1)
二数の場合は、前項と後項を単純に入れ替えても良い
例えば「2:3」の逆比は「3：2」になる
逆比の作り方(2)
それぞれの数(項)を逆数(23→32のように、分子と分母を入れ替えること)にしても逆比が作れる。
「2:3」の場合「12:13」が逆比になり、「1:2:3」の場合「11:12:13」が逆比になります。
ただ、分数のままだと答えとしてはバツになります
単純化する
そこで、上で学んだ「分数の単純化」等で整数比に直します
1-4:逆比の単純化
解説
それぞれの数(項)を逆数にして求めます。
「1:2:3」の場合「11:12:13」が逆比になります。
これを2と3の最小公倍数の6に通分すると、「66:36:26」になって、分子だけを取り出した6:3:2が答えです。
解説
89:315:4→(仮分数に)→89:165:41→(逆数にする)→98:516:14→(16に通分)→1816:516:416→(分子だけ取り出す)→18:5:4
18と5と4には公約数が無い(「互いに素」)ので、これが答え
解説
113:0.6:2→(仮分数に)→43:35:21→(逆数にする)→34:53:12→(12に通分)→912:2012:612→(分子だけ取り出す)→9:20:6
9と20と6には公約数が無い(「互いに素」)ので、これが答え
この単純化で比を自由に扱えるようになったはずですね♪
比の作成と計算
摸試や入試では、計算に使う「比そのもの」は書いていない場合があります。その場合は、問題文から比を作らないといけません。
そこで、指定にしたがって比を作る練習をしましょう。
割合と比
片方の数(項)がもう片方の数に対する割合で指定された場合
割合については関連記事「割合のまとめ」を見て下さい
(6は2の3倍)
(90×0.8)
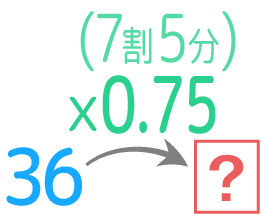
(36×0.75)
実際に比を作ってみましょう。
2-1:割合と比
解説
A:B=1:23になるので、これを単純化します。
1:23で→(3に通分)→33:23→(分子のみ取り出す)→3:2 が答えになります。
ヒント
75%は小数に直しましょう
解説
75%=x0.75 なので、P:Q=0.75:1です。
これを単純化した 3:4 が答えです
ヒント
4割も小数に直して使いましょう
解説
4割=x0.4なので、C:D=1:0.4 です。
これを単純化して5:2が答えです
次は、標準以上の問題でよく見かける指定です
「…と～が等しい」
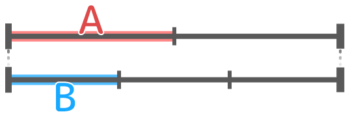
例えば「Aの2倍とBの3倍が等しい」場合、AとBはどのような関係になるでしょうか？
線分図を書くとこうなります。
等しい部分を①とすると、A=12,B=13 になるので
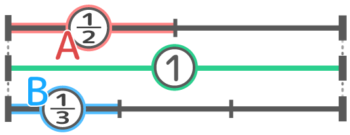
単純化するとA:B=12:13→(6に通分)→36:26→(分子を取り出す)→3:2になります。
つまり、Aの2倍とBの3倍が等しい場合、A:B=3:2 と逆比になるのです。非常によく使うので憶えて下さい
●AのX倍とBのY倍が等しい場合
→A:B=Y:X(逆比)になる
(例)Aの2倍とBの3倍が等しい
→A:B=3:2 になる。
練習問題をどうぞ
2-2:等しい部分
解説
1.2:0.9を逆比にしてA:B=0.9:1.2→(10倍)→9:12→(÷3)→3:4
解説
7割=0.7なので、35と0.7(710)を逆比にして710:35→(10に通分)→710:610→(分子の比)→
解説
分数にそろえると、75%=34、4割=25なので、23:34:25を逆比(逆数)にして、A:B:C=32:43:52→(6に通分)→96:86:156→(分子の比)→9:8:15
文章題で良く出てくるので、必ず憶えて下さい！
比の計算(積と商)
比の数値を他の比の数値や普通の数値とかけたり割ったりすると新しい比が生まれます。
2-3:比の積と商
解説
比の数字と効果1枚の金額を掛け合わせると合計金額の比ができます。
このとき、単位(円など)がある普通の数値と区別できるように、比の数字は記号に入れましょう。
100円玉の合計金額=100x2=200
10円玉の合計金額=10x15=150
この200:150を単純化した4:3が答えになります。
なお、これを計算に使う場合は、記号を丸から変えて4と3にします(新しい比を作る)
分かりましたか？練習問題をどうぞ
2-3:比の積と商
解説
10円玉の合計金額=10x10=100
50円玉の合計金額=50x1=50
100円玉の合計金額=100x2=200
この100:50:200を単純化した2:1:4が答え
解説
合計金額の比の数字6と5を10円と50円で割ると枚数比が出ます。比の数字は記号にいれます。
10円玉の枚数=⑥÷10=610
50円玉の枚数=⑤÷50=550
この610:550を単純化した 6：1 が答えです(これを計算に使う場合は、記号を丸から変えて6と1にします(新しい比))
これで、計算をするために比を作ることも出来るようになりました。
比をそろえる(連比)
2種類以上の異なる比を1種類の比に「そろえる」問題
倍数算など文章題を解くのに用いる
共通部分がある場合
例えばABC3つの数がA:B=4:3、B:C=4:5という関係であるとき、A:B:Cを求めたい
共通するBがそれぞれの比で「3」と「4」になっているので、Bの位置に最小公倍数「12」を書きます
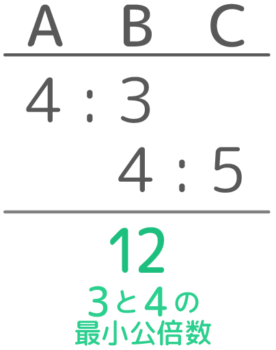
そして、Bが12になるように、残りのAを4倍、Cを3倍する
A:B=4:3→(両方4倍)→16:12
B:C=4:5→(両方3倍)→12:15 になるので、これらをつなげて、A:B:C=16:12:15と分かります。
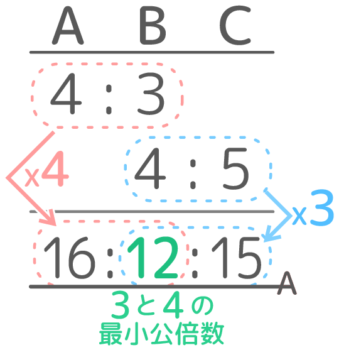
今の作業は共通するBを分母にした比の値4(A)3(B)と5(C)4(B)を16(A)12(B)と15(C)12(B)に通分しているのと一緒です
練習問題をどうぞ
3-1:連比
ヒント
共通しているCを最小公倍数に
解説
共通しているCが6になるように、Aは2倍、Bは3倍します。
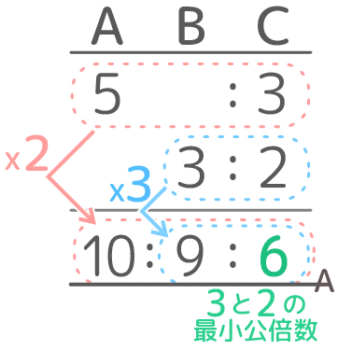
最小公倍数6にする
ヒント
共通しているのは…
解説
共通しているAが15になるように、Bは5倍、Cは3倍
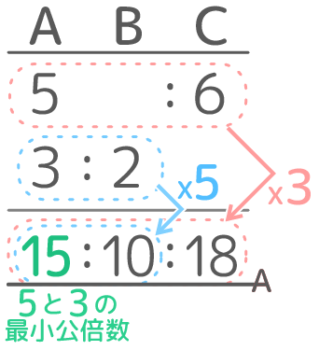
ヒント
まず「単純化」それから「連比」
解説
A:BとB:Cをそれぞれ単純化してから連比にする
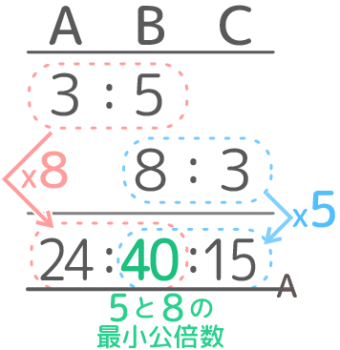
A:B=2.1:3.5=21:35=3:5
B:C=23:14=812:312=8:3
あとは、共通しているBが40になるように、Aは8倍、Cは5倍
ヒント
まずは「単純化」
解説
こちらも単純化したあと連比に。
共通するBが2になるように、Cは2倍、Aは1倍(そのまま)
これで連比の基本は大丈夫でしょう。
加えて「倍数算」で使う「和や差が等しい2組の比」を連比にする作業を憶えておけば鬼に金棒です。
応用(倍数算の準備)
和が等しい比
2022.8.3作成中
差が等しい比
2022.8.3作成中
連比の問題をもっと解きたい人は下にある「オススメ教材」を見て下さい
比例式の解法
比例式
単純化すると等しくなる2つ以上の比を並べた式を「比例式」といいます。
例えば、6:4と15:10はともに単純化すると3:2になります。この2つの比(4つの数値)を並べたものが比例式です。
この4つの数のうち、分からない数が1つある場合…
比例式
「比例式を解く」という
分からない数を求めるのを「比例式を解く」と言います。
内項・外項
比例式を解く前に、大事な事を1つ憶えて下さい。
比例式で4つ並んだ文字と数字のうち、左右の端にある2つを「外項」、真ん中の2つを「内項」と呼びます(図2)
外項
内項
内項
外項
比例式では、外項の積と内項の積が等しくなっています。
●外項の積と内項の積が等しくなる
(例) 6:4=15:10
→内項の積4×15=60と
外項の積6×10=60が
等しくなっている
この例では、内項の積4×15=60と外項の積6×10=60が等しくなっているのが分かります。
これさえ憶えておけば、比例式は簡単です♪
比例式の解法
解法が2つあります。
解法1
「右項と左項に同じ数をかけるか割るかする」という比の基本操作を利用する。
例えば「5:3=?:6」の?を求める場合、右(後項)が3→6と2倍になっているので、左(前項)にも2をかけて5x2=10と分かります。
4-1:比例式の解法1
解説
左(前項)が9→72と8倍になっているので、右(後項)にも8をかけて4x8=32と分かります。
解法2
上の問題は、パッと見で何倍と分かりますが、そうでない場合は多少面倒くさくなります。
例えば「6:9=16:?」の場合、後項が6→16で何倍になっているか調べると、16÷6=83倍になっているので、前項にも83をかけて?=9×83=24と求めることができます
今の計算は「割り算」→「かけ算」と二段階で行いましたが、これを一発で行うのが解法2です。
「内項の積と外項の積は常に等しい」のを利用します
●外項の積と内項の積が等しくなる
(例) 6:4=15:10
→内項の積4×15=60と
外項の積6×10=60が
等しくなっている
先程と同じ「6:9=16:?」の場合、「9x16(内項の積)=?x6(外項の積)」なので、これを逆算して
「?=9x16÷6」
という式が出来ます。
この式を分数にした9 x 166を計算して?=9 x 166=3 x 81=24と、一発で答えが出ます♪
今「内項の積=外項の積」から逆算で作った式「?=9x16÷6」は「内項・外項のうち？でない方(この場合内項)の積を、？と同じ方(この場合外項)の数で割る」という形になっていました。(色に注目して下さい)
この式を一発で作れるように、「A:B=C:D」を例に4つの場合をまとめるとこうなります。
●「A:B=C:D」のとき
A=BxC÷D=B x CD
B=AxD÷C=A x DC
C=AxD÷B=A x DB
D=BxC÷A=B x CA
この分数の式をパッと作れるようにすれば比例式はただの分数の計算になりますね！
さっそく練習してみましょう。
(1)「6:8=A:20」のAは？
「6:8=A:20」
A=6x20÷8= 6 x 208 = 3 x 51 =15
(2)「B:12=21:28」のBは?
「B:12=21:28」
B=12x21÷28= 12 x 2128 = 3 x 31 =9
(3)「52:48=39:C」のCは？
「52:48=39:C」
C=48 x 3952 =12 x 31 =36
(4)「72:D=48:18」のD?
「72:D=48:18」
D=72 x 1848=3 x 91=27
(5)「0.8:1.4=12:E」のE?
小数も分数式にしてから、分母分子に10や100をかけて整数にします
「0.8:1.4=12:E」
E=1.4 x 120.8 →(分子分母10倍)→14 x 128 =21
(別解)0.8:1.4を4:7に単純化してから比例式を作っても良い
(6)「0.36:F=0.6:7.5」のFは？
「0.36:F=0.6:7.5」
F=0.36 x 7.50.6 →(分子分母1000倍)→36 x 75600 =92
(別解)0.6:7.5を2:25に単純化してから比例式を作っても良い
(7)「23:15=10:G」のGは？
分数が混じっていても考え方は同じ
「23:15=10:G」
G=15x10÷23 =1 x 10 x 35 x 2 =3
一発で分数の式が書けるように練習
(8)「517:335=H:258」のH？
まず仮分数にしてから式を作る
「367:185=H:218」
H=367x218÷185=36 x 21 x 57 x 8 x 18=1 x 3 x 51 x 2 x 2 =154 =334
これで文章題でも何でも答えが出せるようになりました♪
比の文章題(1)
通常の比(正比)を使う問題群
比例配分(分配算)
全体の数量と配分の比が示される問題で、以前に学んだ分配算(→関連記事)と同じ考え方で解きます。
端数の無い分配
例題1
5400円をABC3人が5:7:6の比で分けた。Cの取り分は何円か？
全員の比の和5+7+6=18=5400円なので、1=5400÷18=300と分かります。
よってCの取り分6=300×6=1800円です
例題2
お金をABC3人でAとBの比は8:9、BとCの比は6:7になるように分けたところ、AとCの取り分の違いは1600円だった。はじめお金はいくらあったか？
A:B:Cの連比を作ってしまうと単純に解けます。
Bを6と9の最小公倍数18になるように、A:B=8:9を2倍すると16:18、B:C=6:7を3倍すると18:21なので、A:B:C=16:18:21です。
AとCの取り分の差は21–16=5=1600円なので、1=1600÷5=320円です。
全員の比の和16+18+21=55=320×55=17600円と分かります。
半端ある分配
3850円をABC3人で分けた。BはAの2倍より100円多く、CはBの2倍より400円多かった。Bの取り分は何円か？
一番少ないAの取り分を1とすると
B=1x2+100=2+100
C=(2+100)x2+400=(4+200)+400=4+600
となるので、3人の合計は(1)+(2+100)+(4+600)=7+700
7+700=3850だから7=3850-700=3150で、1=3150÷7=450と分かる
B2+100=450×2+100=1000円
二重の分配
全校生徒825人の男女の比は8:7で男子の徒歩通学者と自転車通学者の比は3:2。自転車通学の男子は何人か?
男女の比の合計15=825なので1=825÷15=55人で男子全部8は55×8=440人
徒歩男子と自転車男子の比の合計3+2=5=440なので1=440÷5=88人で、
自転車男子2=88 x 2=176人
図形など、他の分野の知識公式を使った問題もあります。
三角形の内角
三角形ABCの3つの角度の比が3:4:5のとき、一番おおきな角度は何°か？
三角形の内角の和が180°を利用
3+4+5=12=180°→1=180÷12=15°
一番大きな角度5=15x5=60°
長方形の周長
縦と横の比が2:3であり、周囲の長さが30cmである長方形の面積は？
長方形の縦+横=周囲の長さ÷2 を利用
2+3=5=15cm→1=15÷3=5cm
縦=5×2=10cm,横=5×3=15cm なので
面積=10×15=150cm2
比例配分の問題は以上です。
単位量の問題
比を学習する前は1(cm,g等)あたりの量を出して、それを何倍かして求めていましたが、比例式を作ると一発で解けてしまいます。
4-2-1:単位量の問題
解説
「燃料:道のり」の比を作ると「8:162」なので、20Lで走る距離を？kmとすると「20:?=8:162」という比例式ができる
これを解いて?=20×162÷8=20 x 1628=5 x 811=405km(長いですね…東京-大阪の直線距離くらい)
分数のおかげで簡単な計算になっています
練習問題をどうぞ
4-2:単位量の問題
解説
長さ(cm):値段(円)=100:350なので、16cmの値段を？円とすると比例式「16:?=100:350」が出来る
これを解いて、?=16×350÷100=16 x 350100=4 x 141=56円
解説
重さ:値段=100:620。93円の重さを？gとすると「100:620=?:93」
これを解いて？=100×93÷620=100 x 93620=5 x 9331=5 x 31=15g
解説
チョコ:箱=600:50。15箱のチョコを?個すると「?:15=600:50」
これを解いて？=15×600÷50=15 x 60050=3 x 60010=3 x 601=180個
単位量の問題は以上です
狂った時計
基本解法
時計が壊れて正しい時間を刻まなくなった時に「この時計狂ってる」と言いますね。
その狂った時計がこんな感じの問題になります。(修理してくれよ…というのは無しｗ)
4-3:狂った時計
「1時間で3分進む」場合、狂っていない「正しい」時計が1時間(60分)進む間に「狂った」時計は63分進みます。
つまり「正しい」時計と「狂った」時計の進む時間の比は60:63=20:21になります。
正
狂
正
狂
この「20:21」という比は時計を修理しない限りずっと変わらないので、この問題では「20:21」を使った比例式を使えば問題を解くことができます。
では解いてみましょう
4-3-1:狂った時計
解説
「1時間で3分進む」場合、「正しい」時計と「狂った」時計の進む時間の比は60:63=20:21
さて、7時から正午までに「正しい」時計が進んだ時間は(12－7)-1=6時間=60×5=300分で、この間に「狂った」時計が進んだ時間を?とすると「正:狂20(正):21(狂)=300:?」という比例式が出来ます。
正
狂
正
狂
これを解いて、?=300×21÷20=315分。
つまり狂った時計は315分=5時間15分進むので、「狂った時計」が指す時刻は7:00+5:15=12:15分と分かります。
解説
小問1と逆に「狂った」時計が7時から正午まで300分進む間に「正しい」時計が何分進むかを求める問題です。
「正しい」時計が?分進んだとして「20(正):21(狂)=?:300」という比例式が出来ます。
これを解いて、?=300×20÷21=20007=28557分=4時間4557分なので、7時に加えて、11時4557分と分かります(まだ正午になっていないのに「狂った」時計が正午の時報を鳴らします)。
誤差を使う
先程は「1時間で3分進む」場合、「正しい」時計と「狂った」時計の進む時間の比は60:63=20:21 を使いましたが、誤差そのものを比に使うこともできます。
60分で3分(プラス)の誤差なので、60:3=20:1という比ができる
正
誤差
正
誤差
この「20:1」を使った比例式を使う方が解きやすい問題もあります。
4-3-2:狂った時計
解説
(正しい時計で)12時に狂った時計は10分進んでいる。10分の誤差が生じるまでに正しい時計が進んだ時間を？分とすると、「20:1=？:10」という比例式ができる
正
誤差
正
誤差
これを解くと?=200分なので、正しい時計は時刻合わせから12時までに200分進んだと分かる。
200分は3時間20分なので、12:00-2:20=9:40 より、時刻合わせをしたのは9:40分と分かる。
練習問題(2022.8.21作成中)
分数(約分すると…)の問題
例えば「約分すると35になり分母と分子の和が56になる分数を求めよ」という問題
「約分すると35になる」分数は、分子と分母の比が3:5なので、分子を③分母を⑤と置くことができ、③+⑤=⑧=56 ということです。
あとは、分配算として解きます。
分子と分母の和が56
↓
➀=7
分子③=21、分母⑤=35
詳しくは関連記事「分配算まとめ」を見て下さい。
比の積と商
上で説明した、比をかけたり割ったりするのを利用する問題
比の文章題(2)
逆比を用いる問題群です。
等しい部分(明示)
数量
上で説明した通り、「AのX倍とBのY倍が等しい」と書いてある場合 A：B=Y：Xになります。
これを使って分配算のように解きます。
図形(重なりの面積)
また、重なりがある図形の重なった部分(つまり面積が等しい部分)を利用するのも同じです。
等しい部分(暗示)
等しい部分が直接は書かれていない問題
水面から出ている棒
有名なのは「二本の棒が水面から出ている問題」で、この場合水面下の長さが等しくなっています。
例えば「AB2つの棒をプールの底にまっすぐ立てたらAは14がBは15が水面より上に出た。ABの長さの比を求めよ」という場合、水面下にあるのはAの34、Bの45なのでAの34とBの45が等しくなる。
これを逆比にした 43:54がABの比になります。あとはこの比を単純化して(両方12倍)、A:B=16:15と分かります。
金額
確認テスト
Aが貯金の25%,Bが貯金の3割を使ったら残りの金額が同じになった。最初の貯金額の比を求めよ。
→残り金額はAが75%(0.75=3/4)、Bが7割(0.7=7/10)で、これが等しいので、最初の貯金額はA:B=4/3:10/7=(両方21倍)=28:30=14:15と分かる
かみ合う歯車
2つ以上の歯車がかみ合っている場合、歯数と回転数は逆比になります。
例えば、歯数36の歯車Aと歯数24のBがかみ合っている場合を考えます
(図)
AとBの歯数の比は36:24=3:2なので、回転数の比は2:3になります。
この比を利用すると様々な問題を解くことができます。
例題1
歯数36の歯車Aと歯数24のBがかみ合っている。
(1)Aが60回転するとBは何回転するか
Aの歯数:Bの歯数=36:24=3:2 ⇨ Aの回転数:Bの回転数=2:3 なので、Aが60回転するときのBの回転数を？とした比例式「60:？=3:2」を解いて ?=60×2÷3=40回転
(2)A,B歯車の12時方向(上)に印をつける。2つの歯車の印がともに同じ位置に初めて戻るまでにABはそれぞれ何回転するか
印が同じ位置に戻るためには歯車が1回・2回というように整数回だけ回転する必要がある。
ABの回転数の比2:3を両方÷2すると1:32になり、これはAが1回転する間にBは32回転し、AがN回転する間にBは32x N 回転することを意味している。
32x N が整数になる最小のN=2なので、Aが2回転するとBもちょうど3回転して印がもとの位置に戻る。
A2回,B3回
これは、最初に求めた逆比の数値そのものになっている。
2つ(以上)の歯車がかみ合って回転する
●回転数の比は歯数の逆比になる。
(例)歯数36のAと24のBがかみ合って回転
→歯数の比 3:2 →回転数の比は 2:3
●全ての歯車が最初の状態(向き)に戻るのに
それぞれが回転数比の数値だけ回転
(例)歯数36のAと24のBがかみ合って回転
→歯数の比 3:2 →回転数の比は 2:3
→A,Bがそれぞれ2回転・3回転すると
最初の状態に戻る
練習問題
歯数18の歯車Aと30のBと12のCがかみ合っている。
(1)Aが12回転したとき、Cは何回転するか
歯数比は=18:30:12=3:5:2 ⇨回転数比は13:15:12=10:6:15 なので、Aが12回転するときのCの回転数を？とした比例式「12:？=10:15」を解いて ?=12×15÷10=18回転
(2)3つの歯車の12時方向(上)につけた印ががともに同じ位置に初めて戻るまでにABCはそれぞれ何回転するか
回転数比のA10回,B6回,C15回
(3)BとCの回転数の差がちょうど18回になったとき、Aは何回転したか
Aの回転数とBCの回転数差の比は10:(15-6)=10:9なので、比例式「?:18=10:9」を解いて?=20回転
輪軸状の歯車
面積が等しい長方形
面積が等しい2つの長方形のタテとヨコの比も逆比になります。
例えば面積36で等しい長方形AとBがあり、Aがタテ12ヨコ8でBがタテ24ヨコ4の場合
(図)
タテの比は12:24=1:2で、ヨコの比は8:4=2:1、と逆になっています。
この関係を使って「平均算」「」「」等を解きます
二量の関係と表・グラフ
正比例
2つの事柄(数値)が「片方が倍になると、もう片方も倍になる」という関係にあることを「正比例」と言います
例えば毎月500円づつ貯金する時、「月数」が1ヶ月から3ヶ月と3倍になると「貯金額」も500円から1500円と3倍になります。つまり「」と「」は正比例しています。
この時に、「月数」「貯金額」の4つの数値を比にするとこうなります。
反比例
一方、2つの事柄(数値)が「片方が倍になると、もう片方は半分になる」という関係にあることを「反比例」と言います
この時に、それぞれの事柄の比が逆になります。
二量の関係の文章問題
ばね
ろうそく
オススメ教材
爽茶「比」の問題をもっと解きたい人にオススメの教材を紹介
●とにかく比の問題を沢山解きたい人には「比の基礎」(サイパー算数)
●その他の単元の予習復習も合わせて行いたい小5には「算数の基本問題(小5)」(日能研)
●受験算数全体の復習も行いたい小6には「算数ベストチェック」(日能研)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!