「植木算では間の数が大切だな…」と感じている中学受験生の方、あなたは賢いですね！
実は「木」より「間」の方が大切です。東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく解説します。
記事の最後でプリントがダウンロードできます。印刷して書き込みながら解く・教えると効果が倍増するので、ぜひ利用して下さい。
植木算の木と間
こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
実は、「植木算」の問題は、半分以上は「区切り」つまり「間」の問題です。
植木算で使う公式を見てみると(下図)
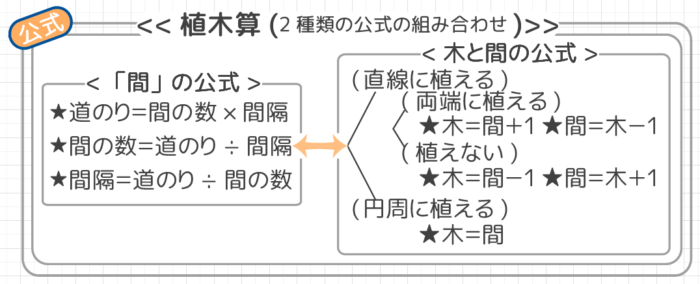
かけ算わり算などメインの計算は「木」ではなく「間」で行っているのが分かります。
そこで、植木算に行く前に、まず間の数の問題を学習して、図の書き方と計算方法(公式)を身につけておきましょう。
間の数の問題
解き方を理解
1:間(あいだ)の処理
解説
まず問題文を読みながら「人がAから歩こうとしている」状況を図にします。
次に、「Bまで8m」とあるので、1mのつもりで点を打っていき(「1」「2」と声に出すと間違えません)、8mまで行ったら標識Bを立てて、「８m」と記入します。
これで準備完了です。
この時点で答が分かる生徒さんも多いですが、図の書き方を憶えるのが目的なので、落ち着いて図を書いていきましょう
問題文にしたがって2mつまり2目盛りごとに旗を立てます。
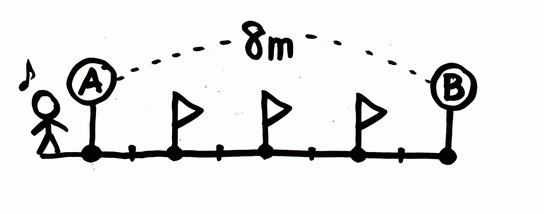
旗の形や色は自由に書かせましょう
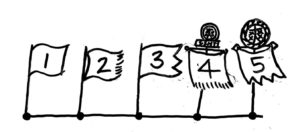
区切れたら、全部の「間」に番号を付けて、間かく「２m」も書き込みます。こちらは１つだけでも良いです。
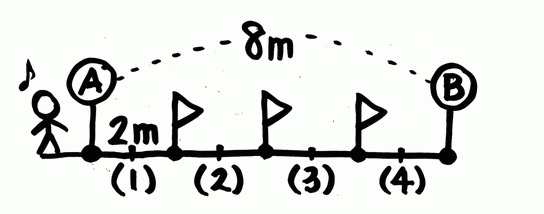
これで図が完成です。答えも「(４)」と出ていますね。
このように、図を書いたら答が出ていたというのが理想です。
ちなみに、この「４」という数を計算で出すには 8÷2 です。
「8」は長さ(m)で「2」は間かく(mおき)なので「間の数(個)＝道のり(m)÷間かく(mおき)」という計算になっています。
このように単位に気をつければ、どういう計算をすればよいのかもわかりやすくなります。
解説
Bの前に立っている人を書き、旗を書いていきます。
先ほどと同じ２mおきですが、慣れたと思うので１mの点は書かずに、同じ間かくで旗を立てて最初に2mを書きます
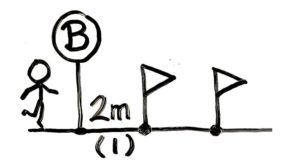
間が10個もあるので、途中を省略する描き方を使います。
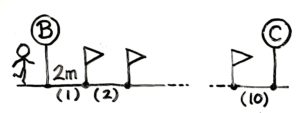
最後の区切りの右端にCを書いて、問題で聞かれているBとCの間の長さ(道のり)は?にします。これで図ができました。
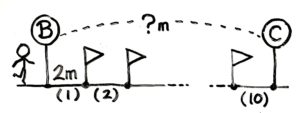
図に？がある場合、？を求めます。図を見れば、2×１0＝２0と分かりますね。
これは「道のり(m)＝間かく(mおき)×間の数(個)」という計算をしたことになります。
解説
慣れてきたので、「C」から35mはなれた「D」まで歩こうとしている人を書いてしまいましょう
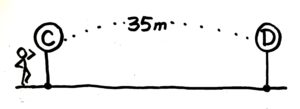
けっこうあるなぁ…とクギリさん
これを7個の間に区切るので、さっきと同じように途中を省略した絵で、間を(1)から(7)まで書きます。
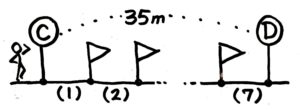
旗の間かく(mおき)は分からないので「？m」と書きましょう
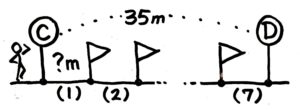
これで図が出来ました。あとは？を出すだけです。
？は35mを7等分しているので、35÷7＝5mおき と分かりますね。
ここでは「間かく(mおき)＝道のり(m)÷間の数(個)」という計算を行いました。
図を丁寧に書いたので、時間がかかったかもしれませんね。お疲れ様でした。
間の公式
今の例題を解くときに、式を3種類使いました。これが「間の公式」です。
(間の公式)
❶道のり(m)＝間かく(mおき)×間の数(個)
❷間の数(個)＝道のり(m)÷間かく(mおき)
❸間かく(mおき)＝道のり(m)÷間の数(個)
できれば、この「日本語のまま」覚えられると、復習の際にもパッと思い出せるようになります(算数が凄く苦手な生徒さんの場合は、具体的な数字を入れた計算で覚えても今のところは構いません)
復習は具体→抽象→具体で行う
また、順番もこのまま覚えられると良いです。
上から、かけ算→割り算→割り算になっていて、かけ算で出している「道のり」が割り算で割られる数になっています。この形は、この後出てくる多くの公式(面積、割合、速さなど)の共通の形です
爽茶では、この公式を使う練習をしましょう。
例題で定着！
できれば公式で解いてほしいのですが、分からない時は図を書いてみましょう。
類題1-1
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale dsd”]
類題では、公式にあてはめる練習を行います。
問題で聞かれていることは「長さ」で、公式には「長さ」というのはありませんね…
実は、
公式を使う場合は、聞かれている数の単位をよく見ることが大切です。
この問題では「何m」ですから、公式のうち「道のり」の式を使えば良い、と分かります。
公式は
①道のり(m)＝間かく(mおき)×間の数(個) なので、
間かく(単位は「mおき」)が3、間の数(単位は「個」)が9なので、3×9=27mと分かります。
答: 27m
もし、
公式を忘れてしまった場合は図を書いてみましょう。こんな感じですね。
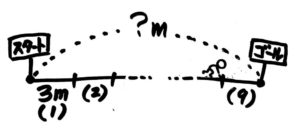
道のり？,間かく3,間の数9を書く
聞かれている数字つまり分からない数字を？として図に書き入れるのが大事です。そうすることで、どうやって求めるか考えることができます。
図を見て、?=3が9個分なので3×9=27mという計算を思いつけばOKです。[/su_spoiler]
類題1-2
単位に注目
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale dsd”]
今度は
「mおき」なので間隔を聞かれていると分かります。
公式の③間かく(mおき)＝道のり(m)÷間の数(個)
に道のり＝24、間の数＝6 を入れて、24÷6=4mおき と分かります
答: 4mおき
もし、公式を忘れた場合は絵を書いてみましょう。
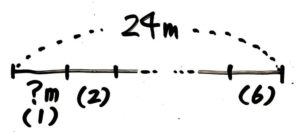
「間かく」に?をハッキリ書くこと
図を書きながら？=24÷6＝4mおき と出せればOKです[/su_spoiler]
類題1-3
ここに考えるヒントや方針
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale dsd”]
「個」を聞かれているので、
②間の数(個)＝道のり(m)÷間かく(mおき) の式を使って
56÷7＝8個ですね
答: 8個
もし公式を忘れた場合は、図を書きます。
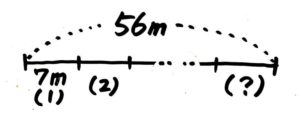
間の個数が(？)と書くこと
56÷7＝8 を思いつけばOKです[/su_spoiler]
今回の問題はこれで終了です。お疲れ様でした！
さて、例題でAからDの標識まで道を区切ったクギリさんは、その後どうしたのでしょうか…というイメージで書いてみましたｗ
気が遠くなる！
まとめとプリントダウンロード
植木算の準備として間の数を図に書き込む
間の公式
❶道のり(m)＝間かく(mおき)×間の数(個)
❷間の数(個)＝道のり(m)÷間かく(mおき)
❸間かく(mおき)＝道のり(m)÷間の数(個)
プリントダウンロード
この記事だけでなくサイトで使っている植木算の問題をコチラでダウンロードできます。
オススメ教材
爽茶●「植木算」(サイパーシリーズ)
●小4まで…和差センス(シグマベスト)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!