無料プリントで小学3年生からの植木算♪円周状に並べた問題の図の書き方と解き方。長方形も【中学受験】

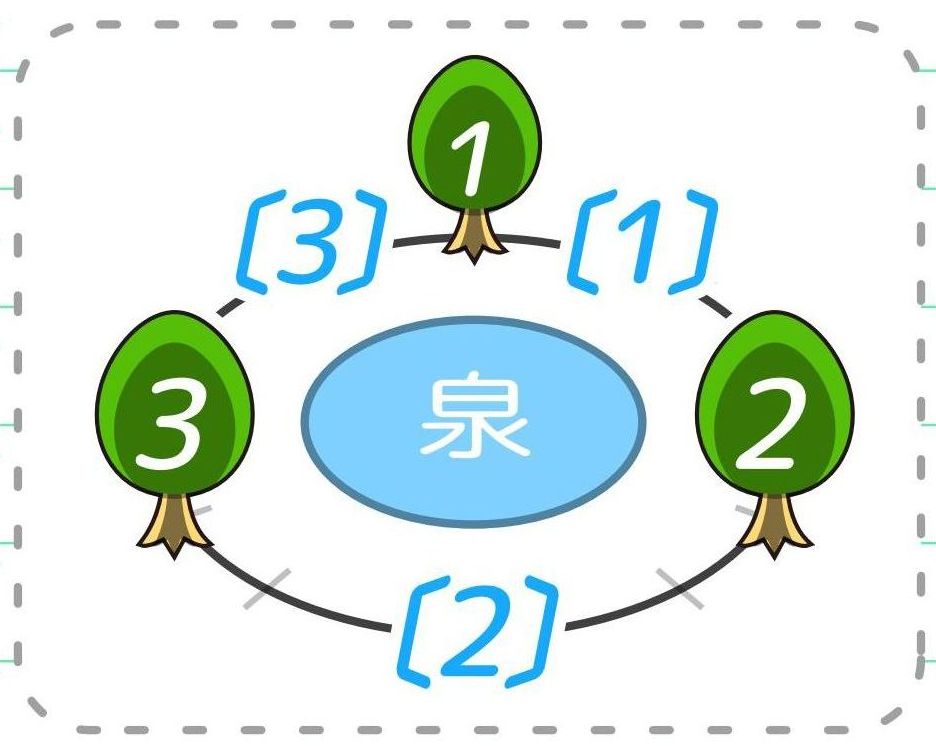
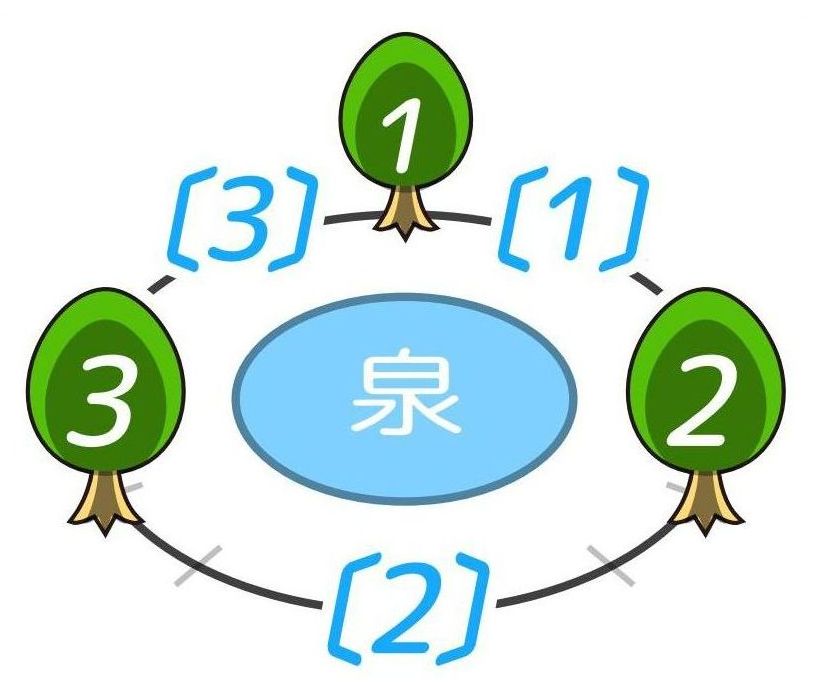
「木を円状に並べるって…何だか難しそう」そう思っている小学3年生と保護者の方へ。実は円状に並べるのが一番簡単なんですよ！東大卒講師歴20年の図解講師「そうちゃ」が詳しく分かりやすく解説します。

間の数と植木(復習)

爽茶そうちゃ

こんにちは！図解講師の爽茶です。前回まで学習した植木算を確認します。

植木算は「間の数」と「木の数と間の数」の2つの公式を使います。

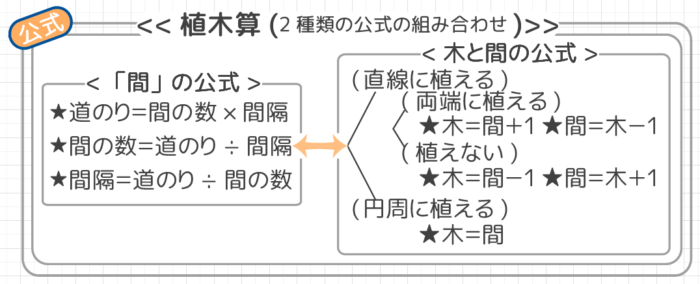
直線上に植える場合は、木の数と間の数は2通りありました。

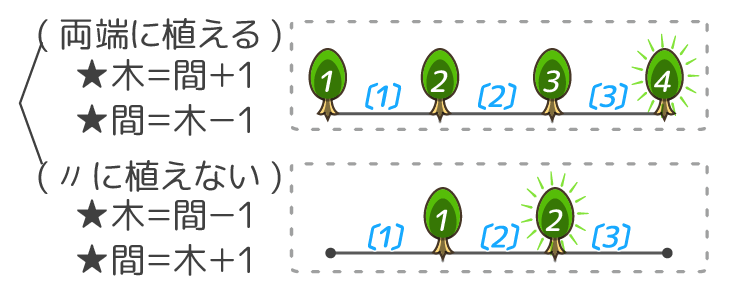
不安な人はテストしてみましょう

テストができなかった人は参考記事「植木算の準備(間の数)」「直線状の植木算」を見てもよいでしょう

円周状に並べた植木算
の解き方

爽茶そうちゃ

直線状に並べた場合よりも簡単ですよ！

解き方を理解♪

例題1

泉の周りを一周する12ｍの道道を4ｍ間かくで区切ると、いくつの間(あいだ)ができますか？

ヒント

円周状に木を植える場合は、上から見た図にするのが簡単で良いですね。

上から道を見ていると思って下さい。

図解

図を書くか、記事のプリントを印刷して書き込んでみれば、3個の間に区切れると分かります。

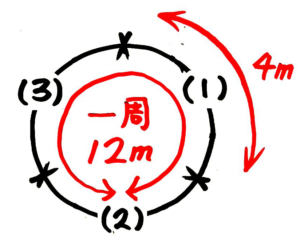
道のり(12)間の数(3)間かく(4)を全て書き込む

3個

または「間の公式」で計算で出してもOKです。

間の公式

①道のり(m)＝間かく(mおき)×間の数(個)
②間の数(個)＝道のり(m)÷間かく(mおき)
③間かく(mおき)＝道のり(m)÷間の数(個)

公式にあてはめる場合は単位に注目します。12は「m」なので「道のり」、4は「ｍ間かく」なので「間かく」です。②を使って、12÷4=3　ですね。

例題1(2)

4ｍ間かくで木を植えると木は何本になりますか？

ヒント

さっきの図に書き込めば分かります。

図解(▼をクリック)

▼

先程の区切った図に木を書き加えると、3本と分かりますね。

木にも番号を書き込みましょう

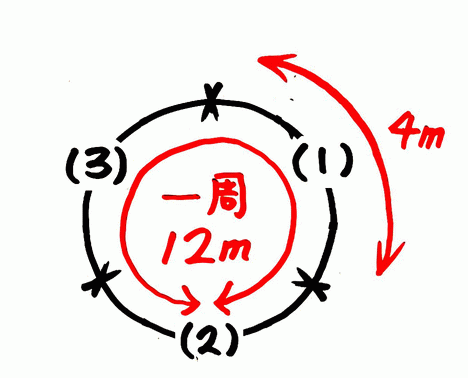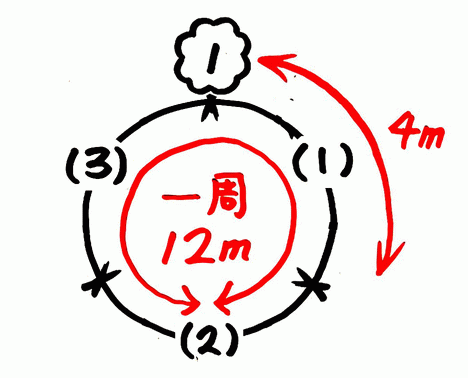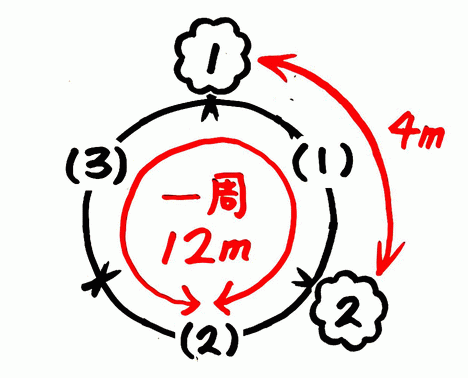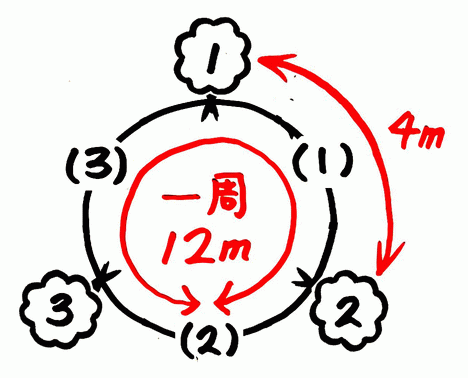
3本

例題1(3)

このように、円周状の道を区切って木を植える場合、木の数と間の数は等しくなります。

直線状の道に沿って植えた場合と、円周状の場合をまとめると、こうなります。

もう少し、覚えやすい形(暗唱しやすい形)にするとこんな感じでしょうか

公式を忘れたときのために(というか忘れにくくするために)、上の3つの図が書けるように練習しておくのが良いでしょう。

問題で定着！

では実際に問題を解いてみましょう。

かけ算わり算などの主な計算は「間の数」で行います。

直線の時と違って「木の数＝間の数」 なので、解きやすいでしょう♪

●類題1

周りの長さが30ｍの池の周りに5ｍおきに木を植えると、木は何本必要ですか？

ヒント

問題文を読みながら、出てきた数字を図にしていきましょう

図解(▼をクリック)

▼

問題文を読みながら図を書くかイメージすると、間の数＝30m÷5mおき＝6個 と分かります。

間を６個、全部キレイに書いても構いませんが、途中を省略する書き方を覚えると図を書くのがラクになります。

最初と最後以外は省略する

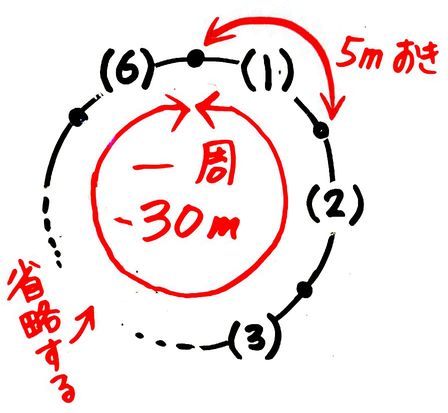
そして円周状に植える場合は、木の数＝間の数なので、木の数も6です。

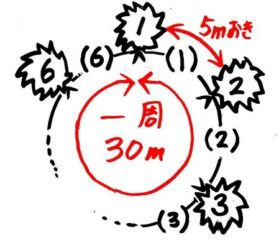
筆が滑って複雑な形にしてしまいましたが(汗)
木はただの丸でOKです

6本

●類題2

花壇の周りに20cmおきに花を植えたらちょうど８本必要だった。花壇の周りは何m何cmですか？

図解

▼

途中を省略して、20と8を図に入れて描くとこうなります

分からない数を？にします

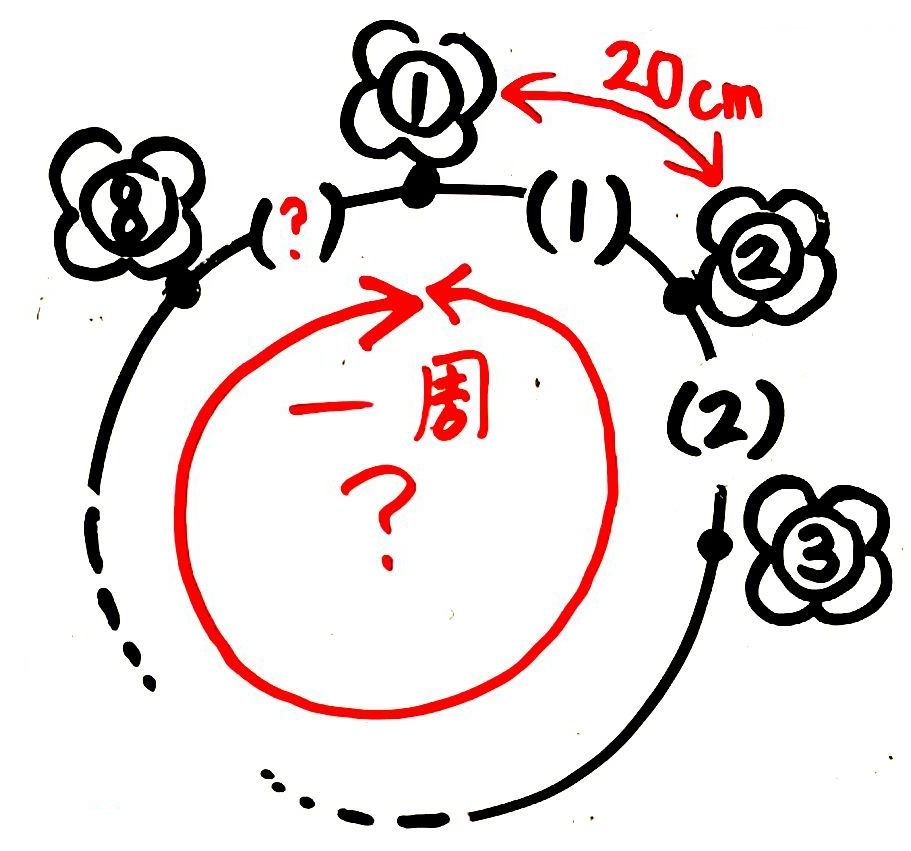
間の数と道のりが分からないで？にしています。

まず、間の数は花の数と同じなので８と分かります。

そして、道のり＝間の数(8)×間かく(20)で160cm=1m60cm が答えです。

単位に気をつけて答えましょう

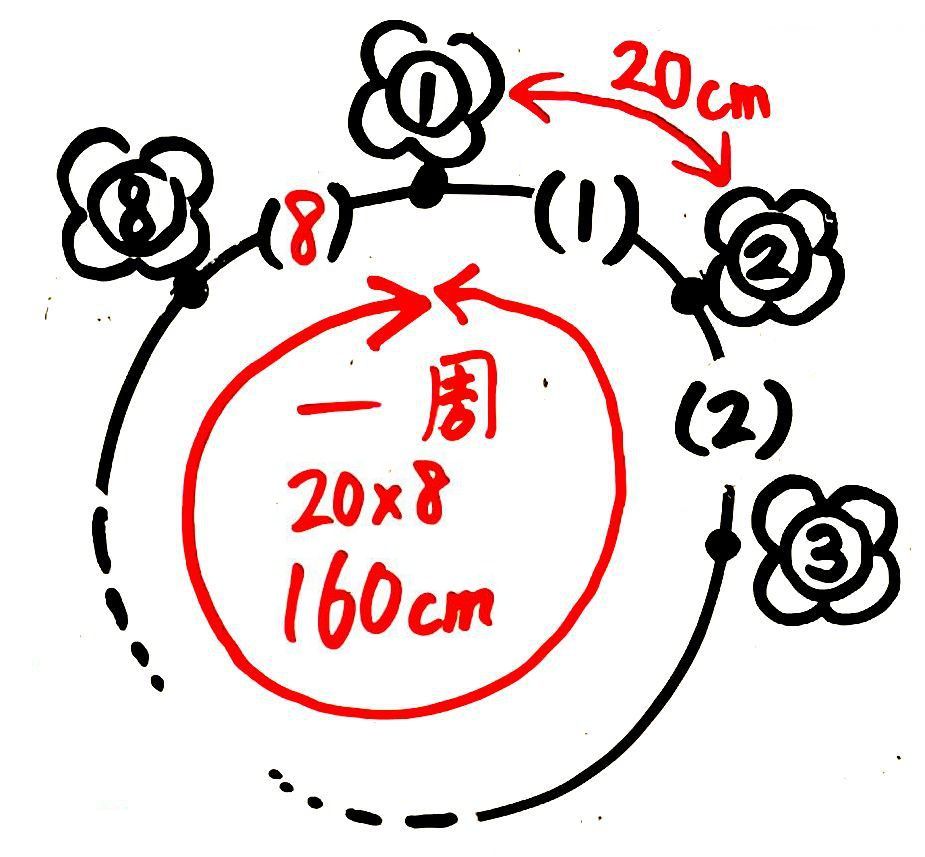
1m60cm

●類題3

63mの遊歩道に7本の旗を等しい間かくで立てたい。何mおきに立てればよいですか？

図解

▼

途中を省略しながら図をかくと、こうなります。

問題文にない間の数と間かくを？に
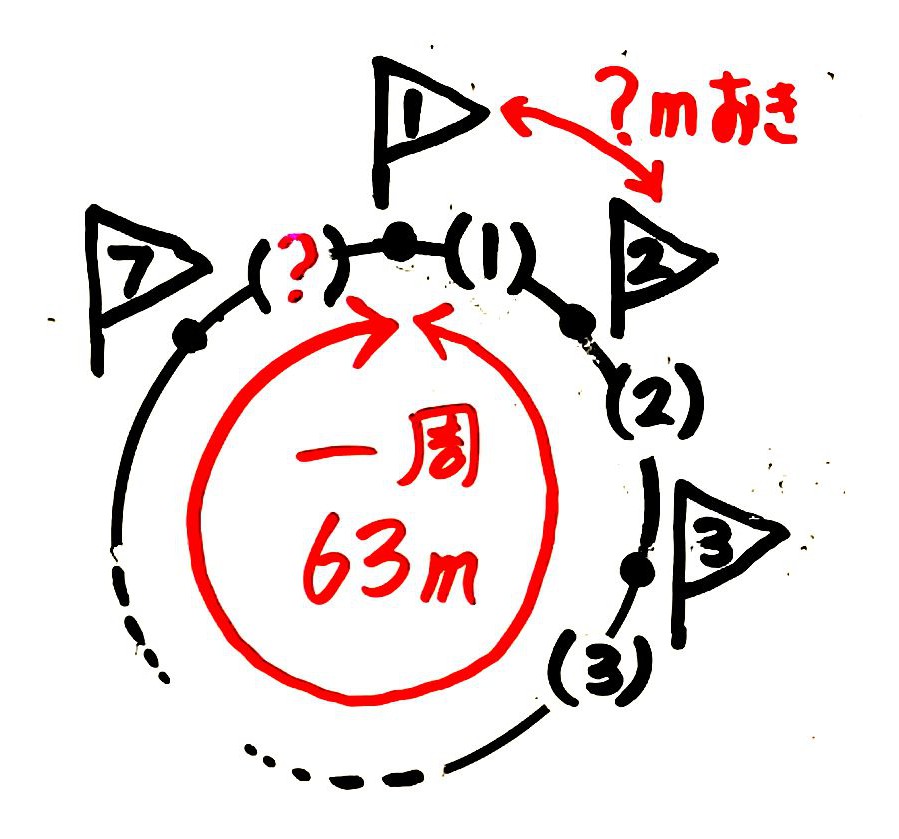?が暗算で分かる人は書き込んでOK

間の数は旗の数と同じなので7個。
間かく＝63m÷7個=9mおきと分かります。

図が完成すると答が出ているのが理想

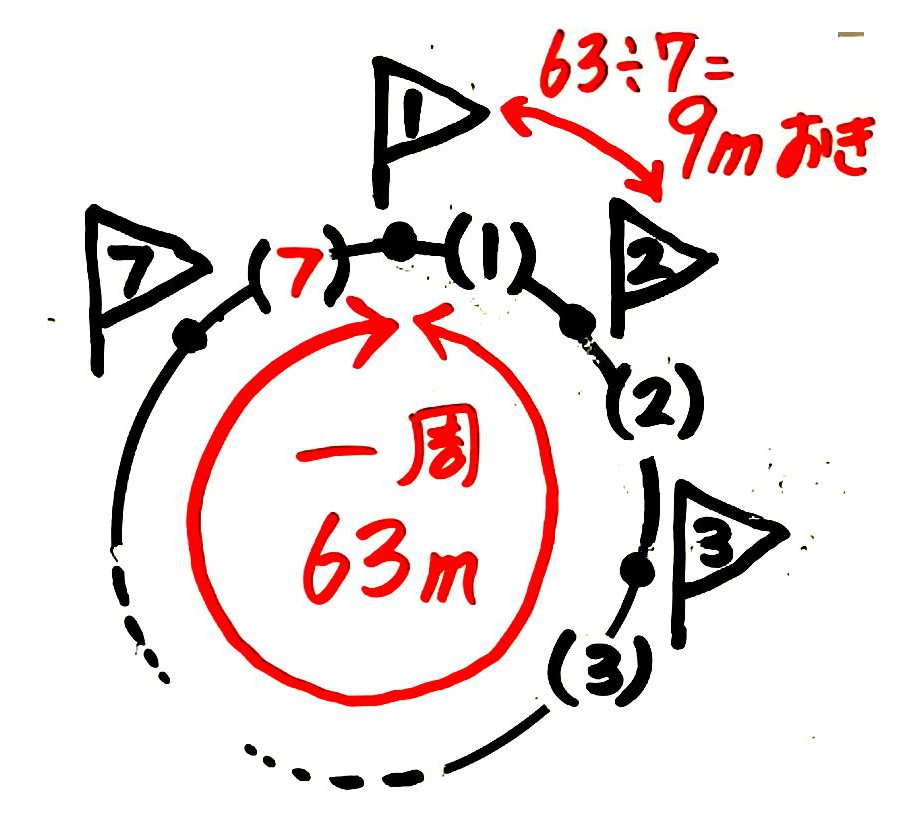
9mおき

●類題4

これで、植木を円周状に植える問題の解法は終了です。

プリントダウンロード

この記事だけでなくサイトで使っている植木算の問題をコチラでまとめてダウンロードできます。

サンプル

問題

&

解答

コチラからダウンロード!

オススメ教材

爽茶そうちゃ

演習の植木算が分かりましたね？「植木算の総合案内」から他の植木算の記事も見て下さい。

もっといろんな問題に触れたい！という人は市販の問題集を使うのも良いでしょう。
●「植木算」(サイパーシリーズ)はとにかく沢山問題を解きたい人向け
●小4まで…和差センス(シグマベスト)は「植木算」や「つるかめ算」を広く浅く学べるので低学年の先取り学習向けです。

2023年度生徒さん募集

2023年度の生徒さんの募集を開始しました(対面授業の一次募集)

東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。

詳しくはコチラのページを御覧下さい

新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから

中学受験でお悩みの方へ

そうちゃ

いつもお子様のためにがんばっていただき、本当にお疲れさまです

受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など

様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。

自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…

そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。

最後まで読んでいただきありがとうございました♪
この記事があなたの役に立てたなら嬉しいです!