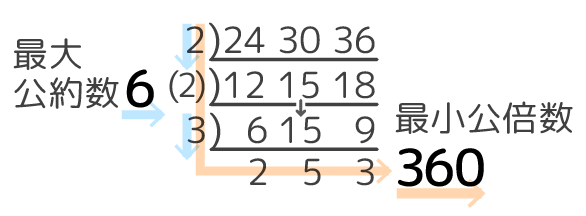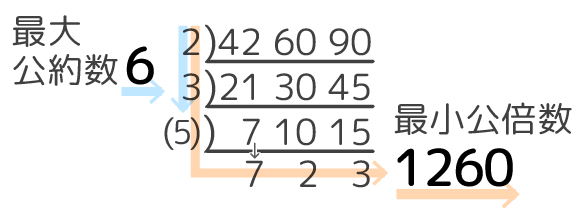「三つの数のすだれ算で最大公約数と最小公倍数を出す方法がよく分からない！」という中学受験生の方、確かに三つの場合は少し面倒くさいです…でも安心して下さい！東大卒講師歴20年の図解講師「そうちゃ」が分かりやすくまとめます！
すだれ算がよく分からない人は「倍数約数まとめ」内の「すだれ算」を読んで下さい。
なお、記事の終わりでプリントがダウンロードできます。
三つの数の
最大公約数・最小公倍数
(素因数分解)
爽茶こんにちは！図解講師の爽茶です(2018//)。
まずは、素因数分解を使った解法です。前回と考え方は同じなので、気楽に解きましょう♪
例題1
12と18と30の最大公約数と最小公倍数を求めたい
- 12と18と30を素因数分解の形にして、約数ごとにタテにそろえて横に並べなさい。
- 今作った「横並び」を元に、最大公約数を求めなさい
- 最小公倍数を求めなさい。
●1-(1)
前回、12と18を因数分解して並べたのが下の図です。共通する素因数(約数)の「2」と「3」が一つずつタテにそろえられているのが分かります(太字の数)。コレを参考にして下さい。
18=2×2×3×3
[su_spoiler title=”解説と解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
30を素因数分解すると、30=2×3×5 ですね。
(これが分からない人はココを見て下さい)
12と18と30に共通する素因数は「2」と「3」なので、その2つをタテにそろえて横に並べるとこうなります↓
18=2×2×3×3
30=2×2×3×3×5
[/su_spoiler]
この図を使えば、色んなことが分かります。
●1-(2)
いくつかの数が共通して持つ素因数をかけたものが最大公約数になります。
12と18の場合は、タテにそろった共通する素因数は「2」と「3」なので、2×3=6が最大公約数になります。
12=2×2×3
18=2×2×3×3
☆ 2×2×3×2=6(最大公約数)
[su_spoiler title=”解説と解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
12と18と30が共通して持つ(タテにそろっている)素因数は「2」と「3」なので、それらをかけ合わせた6が最大公約数になります(たまたま同じ答えになりました)
18=2×2×3×3
30=2×2×3×2×5
☆ 2×2×3×2×2=6(最大公約数)
答: 6[/su_spoiler]
この図を使うとまだ分かることがありますね。
●1-(3)
いくつかの数がもつ全種類の素因数の積が最小公倍数になります。
12と18の場合は、登場する全ての因数をかけ算して最小公倍数は36になりました。
18=2 ×3×3
☆ 2×2×3×3 =36(最小公倍数)
[su_spoiler title=”解説と解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
12と18と30が持つ素因数を全種類かけ合わせて、最小公倍数は180になります。
18=2 ×3×3
30=2 ×3 ×5
☆ 2×2×3×3×5 =180(最小公倍数)
答: 180[/su_spoiler]
爽茶次は、同じ事をすだれ算でやってみましょう！
三つの数のすだれ算
(通常型)
爽茶解法を理解しよう♪
例題2
12と18の場合は、すだれ算はこうなりました。
3) 6 9
2 3
[su_spoiler title=”すだれ算を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
まず、12と18と30を並べて書き…
↓
12と18と30を全部割り切れるできるだけ小さい素数を考えます…２ですね。12と18と30を2で割り、答えを下に書きます。
6 9 15
↓
次は、6と9と15を全部割り切れる一番小さな素数を考えます…3ですね。6と9と15を3で割り、答えを下に書きます
3) 6 9 15
2 3 5
2と3と5は全部が素数なのでもう割れません。ここで終了です！[/su_spoiler]
では、最大公約数と最小公倍数を答えて下さい。
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
3) 6 9 15
2 3 5
(最大公約数)
2×3
(最小公倍数)
2×3×2×3×5
左に並んでいるのが12と18と30に共通する素因数なので、その積が最大公約数,左と下に並んでいるのが全種類の素因数なので、その積が最小公倍数になります。
答: 最大公約数6,最小公倍数180
さっきやった素因数分解式の図はこうでした。同じ計算になっています。
18=2 ×3×3
30=2 ×3 ×5
☆ 2×2×3×2×2=6(最大公約数)
☆ 2×2×3×3×5 =180(最小公倍数)
[/su_spoiler]
このように、三数といっても二数の場合と違いはありませんね♪
さっそく、類題で練習しましょう！
( ･`ω･´)
練習問題で定着！
類題2-1
[su_spoiler title=”すだれ算を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
3)27 45 63
3) 9 15 21
3 5 7
[/su_spoiler]
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
すだれ算が分かれば
3)27 45 63
3) 9 15 21
3 5 7
(最大公約数)
2×3×3
(最小公倍数)
2×3×3×3×3×7
答えは分かりますね。
答: 最大公約数18,最小公倍数1890
[/su_spoiler]
類題2-2
[su_spoiler title=”すだれ算を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
3)150 375 525
5) 50 125 175
5) 10 25 35
2 5 7
[/su_spoiler]
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
すだれ算ができれば
3)150 375 525
5) 50 125 175
5) 10 25 35
2 5 7
(最大公約数)
2×3×5×5
(最小公倍数)
2×3×5×5×2×5×7
答えは分かりますね。最小公倍数のかけ算が少し面倒くさかったかもしれませんね
答: 最大公約数150,最小公倍数10500
[/su_spoiler]
爽茶三つの数のすだれ算
(変則)
爽茶「変則」すだれ算を理解する
例題3
どこが「変則」かを理解して下さい
とりあえず、すだれ算を始めてみましょう
↓
14,20,30全部を割れる最小の素数…2で割ります
7 10 15
7と10と15の全部を割れる素数…無いですね。では、これで終了！
と思いきやまだ終わりではないのです!!
7と10と15の全部を割れる素数はありませんが、10と15の2つなら5で割れますね。5で割りましょう
↓
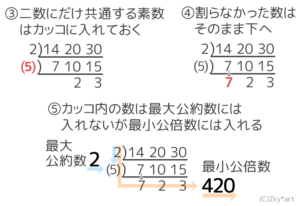
ただし！この「5」は全部を割れる数ではないのでカッコの中に書いておきます
場合はカッコに入れる
2)14 20 30
(5)) 7 10 15
↓
そして、7は5で割れないので、そのまま下におろします
そのまま下におろす
2)14 20 30
(5)) 7 10 15
7 10 15
↓
10と15は5で割った答えを下に書きます。
(5)) 7 10 15
7 2 3
7,2,3は全部素数なので今度こそ、完了です！
このように、途中で二数しか割れない素数が出てきた場合はちょっと特殊なやり方(変則すだれ算)になるのです。
そして、この場合の最大公約数に(5)は入れてはダメ!です。なぜなら、三数に共通な数では無いからです。
ただ、(5)も最小公倍数の式には入れます。20と30の約数ではあるからです。
というわけで、こうなります。
(5)) 7 10 15
7 2 3
(最大公約数)
2
(最小公倍数)
2×(5)×7×2×3
()無しの左の積が最大公約数で、左と下の積が最小公倍数
答: 最大公約数2,最小公倍数420
これが変則すだれ算です。
二つの数しか割れない場合、最大公約数に注意
ちょっと紛らわしいですね…
(^_^;)
類題で練習して身につけて下さい。
練習問題で定着！
類題3-1
❶二数しか割れない数はカッコに入れる。
❷割ることが出来ない数はそのまま下に
ですよ
[su_spoiler title=”すだれ算を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
はじめに2で割った後は、三数を割れる素数がありません
(>_<)
12 15 18
↓
しょうがないので、2で12と18を割って、15はそのまま下におろします。この2をカッコにいれるのを忘れずに！
(2))12 15 18
6 15 9
↓
今度は、3で全部割れます
(2))12 15 18
3) 6 15 9
2 5 3
全部素数になったので、完了です!
[/su_spoiler]
これで答えが分かりますね
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
最大公約数は(2)は入れないので「2×3」になりますが、最小公倍数は(2)を入れるので「2×(2)×3×2×5×3」になります。
(2)の扱いに注意しましょう
答: 最大公約数6,最小公倍数360
[/su_spoiler]
できましたか？もう一問やってみましょう。
類題3-2
[su_spoiler title=”すだれ算を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
最後の5が二数しか割れないので、
3)21 30 45
(5)) 7 10 15
7 2 3
5をカッコに入れて、7はそのまま下ろします。
[/su_spoiler]
これで答えが分かりますね
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
(5)は最大公約数のかけ算には入れないが、
最小公倍数のかけ算には入れます。
答: 最大公約数6,最小公倍数1260[/su_spoiler]
ここまでは慣れてもらうために「2」で三数を割ることができるような問題にしてきました。
慣れてきたら「2」で三数を割れない場合も、あせらずに二数を割れないか検討して下さい。
類題3-3
一番小さい素数「2」から検討していきましょう
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
いきなり2で三数を割れませんが、二数は割れるのでカッコに入れて割り算します。割れない45はそのまま下へ。
9 15 45
↓
さらに進んでいくと、二数しか割れないのが連続しますが、落ち着いて丁寧に処理しましょう。
3) 9 15 45
(3)) 3 5 15
1 5 5
↓
面倒くさい問題でした。
3) 9 15 45
(3)) 3 5 15
(5)) 1 5 5
1 1 1
三数を共通して割れるのは二段目の3しかありませんでした…
最大公約数は3で、最小公倍数は全部の数をかけるので、(2)×3×(3)×(5)×1×1×1=90 です。
答: 最大公約数3,最小公倍数90[/su_spoiler]
爽茶まとめと
プリントダウンロード
三数のすだれ算(最大公約数・最小公倍数)
二数しか割れない素数がある場合に最大公約数に注意！
()無しの左の積が最大公約数
左と下の積が最小公倍数
プリントダウンロード
画像をクリックするとプリントが表示されますので保存して下さい。メアド等の入力は必要ありませんが、著作権は放棄しておりません。無断転載引用はご遠慮ください。
次のステップへ
爽茶→(公)約数/倍数のまとめに戻る
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!