「素数(そすう)？素因数？分解？何それ？」という中学受験生の方へ、ご安心下さい！
東大卒講師歴20年の図解講師「そうちゃ」が素数の意味から素因数分解さらに「すだれ算」まで分かりやすく説明します。
記事を読んで真似すれば、この範囲はもう大丈夫です。特に「すだれ算」はとっても便利なので是非マスターして下さい！
なお、記事の最後でプリントを自由にダウンロードできます。
素数(そすう)って何？
素数の意味と見分け方
前回の記事「約数の意味と求め方」で、約数をもとめる時に、数をA×Bというように分解しましたね。
例えば、18は「1×18」「2×9」「3×6」と三通りに分解できました。
では、6はどうでしょうか？
前回と同じ考え方で「1×6」「2×3」と二通りに分解できますね。
今度は3はどうでしょうか？
「1×3」と一通りにしか分解できません
( ・Θ・)
2もそうですね。「1×2」と一通りにしか分解できません
( ・Θ・)
今の3や2のような「1×その数」と一通りにしか分解できない数を「素数(そすう)」と言います。
→「1×その数」という形にしか分解できない数
面倒くさい！と思う人もいるかもしれませんが「素数」はとても便利な道具なんですよ！！
そこで、どんな素数があるのかを見ていきます。
10までの素数
10までの数が素数か調べてみましょう
1-1:素数の識別
ヒント
かけ算に分解して調べましょう
解説
分解してみて、「1×その数」にしか分解できなければ素数です。1から順に調べていきます。
まず最初の「1」は素数でしょうか？
鋭いあなたは「1×1」には直せるからいいんじゃないの？と思ったもしれませんがこれを許すと「1×1×1」「1×1×1×1」…というように無限に作れてしまうので、1は分解できない！とされています。
したがって、1は素数ではありません
次の 2,3はさっき見たとおり、それぞれが「1×2」「1×3」と一通りにしか分解できなかったので、素数です
では、その次の「4」は素数でしょうか？
4は「1×4」「2×2」 と2通りに直せるので素数ではありません
ここまでの結果を表にすると、こうなりますね。
| 数 | 分解した形 | 素数？ |
| 1 | 分解できない | No |
| 2 | 「1×2」だけ | Yes |
| 3 | 「1×3」だけ | Yes |
| 4 | 「1×4」と「2×2」の2つ | No |
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
では、表の残りの箇所を埋めて、素数が全部で何個あるか出して下さい！
こうなりますね
| 数 | 分解した形 | 素数？ |
| 1 | 分解できない | No |
| 2 | 「1×2」だけ | Yes |
| 3 | 「1×3」だけ | Yes |
| 4 | 「1×4」と「2×2」 | No |
| 5 | 「1×3」だけ | Yes |
| 6 | 「1×6」と「2×3」 | No |
| 7 | 「1×7」だけ | Yes |
| 8 | 「1×8」と「2×4」と「2×2×2」 | No |
| 9 | 「1×9」と「3×3」 | No |
| 10 | 「1×10」と「2×5」 | No |
「素数」=「1×その数にしか直せないもの」は 2,3,5,7 の4個と分かります。
この後、素数は 11,13,17,19…と無限に続いていきますが、特に大切なのは「2,3,5,7」この4つです。
●素数とは
→「1×その数」という形にしか分解できない数
(例) 2→素数,3→素数,1→違う,6→違う(2×3に分解できる)
●よく使う基本的な素数→2,3,5,7
爽茶この後は、素数を使ったワザ「素因数分解」です！
素因数分解のやり方1
(2分解式)
やり方を理解♪
2-1:素因数分解(2分解式)
ヒント
答えは1つではありません。どれか1つが言えればOKです。
解説
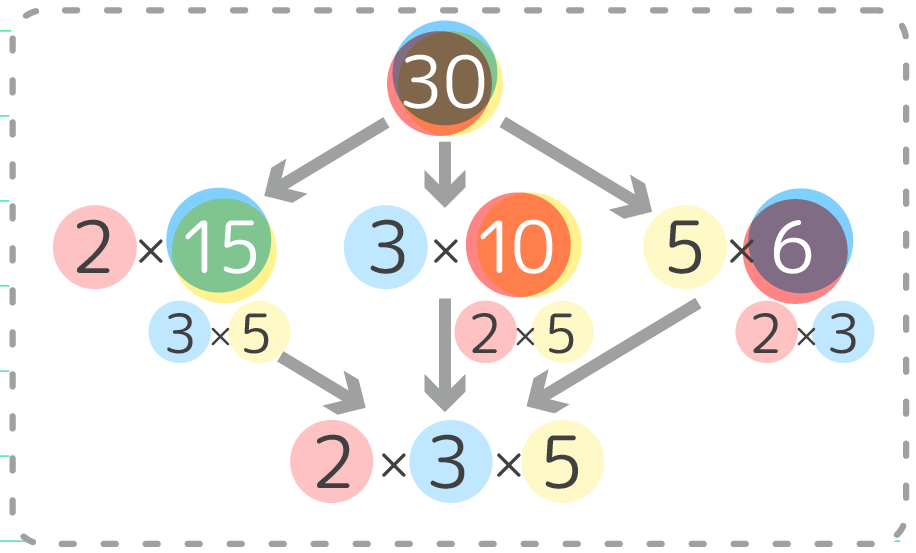
3種類の直し方があります。「2×15」「3×10」「5×6」このどれでも良いです
1を使っていけない理由はさっきと同じで「…×1×1×…」といくらでも書けてしまうからです。
(解答)
小問1の答えが「2×15」「3×10」「5×6」の3つあったので、順に直していきましょう。
例えば、「2×15」の場合、15を3×5に分解して「2×3×5」という3数のかけ算になります。
では、「3×10」の場合どうなりますか？
10を2×5に分解して「3×2×5」という3数のかけ算になりますね。
また、「5×6」の場合は？
6を2×3に分解して「5×2×3」という3数のかけ算になります。
いずれの場合も、小さい順に並べ直すと「2×3×5」という3数のかけ算に分解できます。
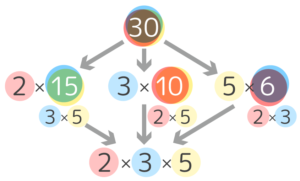
最後は 2×3×5 になりますね
もう気付いたと思いますが、素数だけのかけ算に直していたのですね(1は素数ではありませんでしたね)
このように、素数だけのかけ算に分解することを素因数分解と言います。
素因数分解は、数の問題では必ずと言っていいほど使うことになる超重要事項です。
→素数だけのかけ算に直すこと
類題で「ニ分解式」を身につけましょう♪
練習問題で定着♪
類題1
まず、63を2数のかけ算に分解すると(1は使ってはいけません)
「3×21」「7×9」のどちらかになりますね。
次にこれを更に3数に分解すると
「3×21」の場合はさらに21を3×7に分解します
「7×9」の場合さらに「9」を3×3に分解します
どちらの場合も、できた3数を小さい順に並べると 3×3×7 になります。3×3×7
これで素因数分解完成です。
爽茶素因数分解のやり方2
(すだれ算)
爽茶さて、さっきの2分解から3分解に直す方法でも素因数分解はできますが、よりスマートに、そして公約数や公倍数にも応用が効くワザを紹介します。
それが「すだれ算」です
「すだれ」って何？
知らない小学生もいると思うので…
↑これが「すだれ」です。使わないときは上に丸めておいて、使う時に下に伸ばすものです。言ってみれば昔のブラインドカーテンですね！
何と！奈良時代(710～793)からあったそうなので、1300年前から使われている！！すごいですね
「下に伸ばす」というのがポイントです
やり方を理解♪
話を戻しまして…
(^_^;)
先程、「2分解式」で 2×3×5に素因数分解した30を、今度は「すだれ算」で素因数分解してみます。
例題3(素因数分解2)
30を「すだれ算」で素因数分解します。以下の問いに答えなさい。
- 30をできるだけ小さい素数で割って「すだれ」で書きなさい
- 上の答えをできるだけ小さい素数で割って「すだれ」で書きなさい。
- すだれ算の結果を書きなさい
例題3-(1)
「すだれ算」は、割り算の一種です。ただ、普通の割り算と違って「素数」でしか割れません
ここでは30を割り切れる「素数」を考えます。できるだけ小さいものが良いです。何でしょうか？
素数は小さい方から2,3,5,7…でした。30を割り切れて一番小さいのは2です。
そして30÷2=15なので、これを「すだれ」にすると…
変な形ですね
(^_^;)
普通の割り算の筆算を思い出して見比べてみます
2)30
20
10
10
00
こう見ると、書いてある数字は全く同じです。すだれ算は答えを下に書いていく割り算だと思って下さい。
下に伸びていくので「すだれ算」なんですね！
→わり算の答えを、上では無く下に書いていく形
さて、すだれ算はここで終わりではありません。
例題3-(2)
今度は、先程の答え15をできるだけ小さい素数で割ります。どうなりますか？
2,3.5.7…のうち、2は無理で、3で割れますね。
15÷3＝5 をすだれ算にすると…
15÷3=5
こうなります。
例題3-(3)
小問2の答えの5は素数なのでm、これ以上割り算ができず、すだれ算は終了になります。
完成したすだれ算の左と下には、素数が 2→3→5 と書いてあります。
これは 30＝2×3×5 と素因数分解できたという意味です。
と分解できた
実は、「すだれ算」とさっきの「2分解式」は、やっていたことは同じです。
30=2×3×5
爽茶問題で定着！
類題3-1
まず105をできるだけ小さい素数で割ります。
割れるかどうかの判断は、以前「倍数の見分け方」で説明しましたね。特に大事なのは次の3つです
●2の倍数
1の位が「0,2,4,6,8」なら2で割り切れる
●3の倍数
各位の和が3の倍数なら3で割り切れる
●5の倍数
1の位が「0,5」なら5で割り切れる
では、105を２，3，5のうち一番小さいもので割って、すだれ算の形にして下さい。
まず、1の位が5なので2では割り切れません。次に、1+0+5＝6なので、3では割り切れます。
105÷3＝35を すだれ算で書くと、こうなります。
次に35をできるだけ小さい素数で割って、すだれ算にしてください。
35÷5＝7ですね。先程のすだれ算に、これを書き足すと
こうなりますね。
7は素数なので、これで終了です。
105＝3×5×7 と素因数分解できました。105＝3×5×7[
ところで、105を見た時に多くの人が「5の倍数だな」と感じると思います。
では最初の割り算を 105÷5＝21 としたら、どうなるでしょうか？
すだれ算はこうなりますね
数字が、5→3→7という順番にならんでいますが、答えを書く時に「3×5×7」の順に直せば、OKです♪
類題3-2
2,3で割っていくと…
こうなるので…84＝2×2×3×7と素因数分解できます。84＝2×2×3×7
類題3-3
すだれ算を作ると…
こうなるので…2×2×3×5×5と素因数分解できます。300＝2×2×3×5×5[
類題3-4
数が大きくなっても同じようにやりましょう
すだれ算を作ると…
こうなるので…2×3×3×7×11と素因数分解できます。1386＝2×3×3×7×11[
爽茶まとめとプリントダウンロート
●素数＝「1×その数」にしか分解できない数
●素因数分解=素数のかけ算に分解すること
(例:30を素因数分解すると、30=2×3×5 )
●すだれ算=答えを下に書いていくわり算
●すだれ算による素因数分解
3)15
5
記事で使った問題の解説プリントをダウンロードできます。画像をクリックするとプリントが表示されますので保存して下さい。
著作権は放棄しておりません。無断転載引用はご遠慮ください。
爽茶●単元学習中の小4・小5には定評のある「算数の基本問題(小5)」(日能研)
●サッと復習したい小6受験生には「算数ベストチェック」(日能研)
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!