「倍数の応用問題に挑戦したい」という小学5年生や中学受験生の方、お任せ下さい!
東大卒講師歴20年の図解講師「そうちゃ」が「~で割ると…余る数」をまとめました♪
この記事を読めば得点アップ偏差値アップできますよ!
~「で」割ると余りが出る数
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
「~で割ると~余る」はどのような 数のことなのか、誘導形式の例題で理解して下さい。2つの表現方法を理解
1-1:倍数と余り
解説
「Aで割り切れる数」=Aの倍数でした。(忘れたという人は「倍数の意味と範囲」を見て下さい)
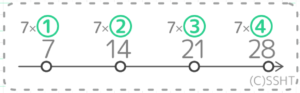
したがって、「7で割り切れる数」=7の倍数です
7×➀(=7),7×➁(=14),7×③(=21)…と増えていきます
解説
「3余る」とは言葉としては「プラス3する」 という意味ですね。この問題では、7の倍数に+3するという意味です。
よって「7で割ると3余る数」は「7の倍数+3」になります
先程の7の倍数にプラス3した数を並行する数直線に記していくと、10,17,24…と増えていきます。
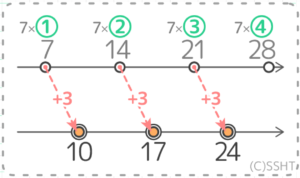
ただ!これで終わりではありません!
解説
10を14と、17を21と結んでみると…
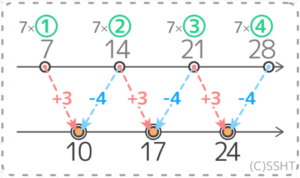
BはAをマイナスの方向に4ずらした数になっていると分かります。
つまり、Bは「7の倍数-4」とも言えるのですね。
解説
先程のプラスとマイナスの2つの考え方を合わせて
「7で割って3余る数」は「7の倍数+3」または「7の倍数-4」と言えますね
このように、割ると余りが出る数は「倍数にプラスする型」と「倍数からマイナスする型」の2通りの表現があります。
o(・∀・)o
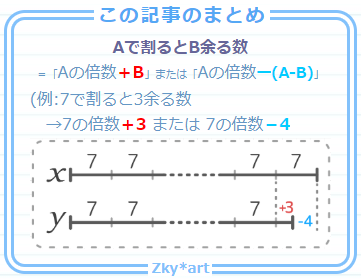
「Aで割るとB余る数」
◆プラス型表現「Aの倍数+B」
◇マイナス型表現「Aの倍数ー(A-B)」
(例)7で割ると3余る数
◆プラス型の表現「7の倍数+3」
◇マイナス型の表現「7の倍数-4」
線分図での表現
先程は数直線で説明しましたが、線分図での書き方を記しておきます。(こちらの方もよく使います)
まず、「7で割り切れる数=7の倍数」を線分図にすると、こうなりますね。
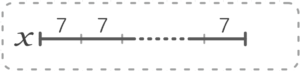
(かけ算の線分図と同じ)
次に「7で割ると3余る数」Bを書きます。上でまとめた通り、Bはプラスマイナス2通りの表現が可能です
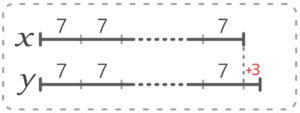
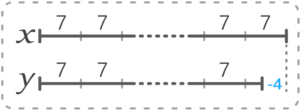
そして、2つを合わせて図にするとこうなります
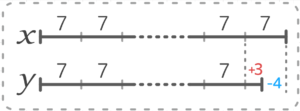
マイナス型(7の倍数ー4)
2通りの表現が可能
是非書けるようにしておきましょう!
「Aで割るとB余る数」
◆プラス型表現「Aの倍数+B」
◇マイナス型表現「Aの倍数ー(A-B)」
(例)7で割ると3余る数
◆プラス型の表現「7の倍数+3」
◇マイナス型の表現「7の倍数-4」

類題で定着
1-1:倍数と余り
解説
問題文で「13で割ると3余る」とあるので、
13の倍数にプラスする数字は3、マイナスする数字は 13–3=「10」です
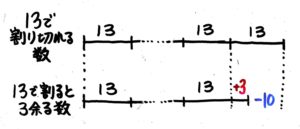
こういうイメージ(汚くてスイマセン)
したがって、プラス型の表現は「13の倍数+3」、マイナス型の表現は「13の倍数-10」です。
それでは、これら表現を使った問題を解いてみましょう。
利用問題
考え方を理解
1-1:倍数と余りの問題
解説
「9でわると6余る数」は「9の倍数プラス6」または「9の倍数マイナス3」と表現できます。
プラス型の表現を使って考えると、9の倍数が ①9,②18,③27…と増えていき、それに6をプラスすると 15,24,33 になります
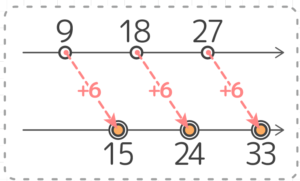
ところが「マイナス」の方を使うと、6,15,24 になります。
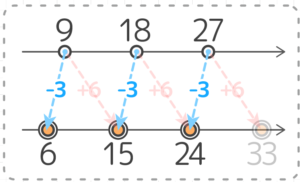
こちらの方が数が「最初の3つ」ですね
したがって、答えは 6,15,24 になります
補足…
プラス型の表現の場合、先程の図には9の倍数のゼロ番目0というのが隠れていて、9×0+6=0+6=6 が最初の数だったのですね!
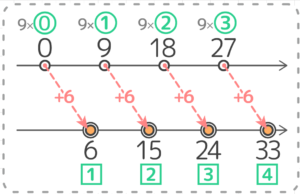
ただ、この考え方だと9の倍数のゼロ番目と「余る数」の1番目が対応することになり、紛らわしいです…
一方、マイナス型の表現だと、9の倍数の1番目「9」と6余る数の1番目「6」が対応するのでスッキリ分かりやすいです。
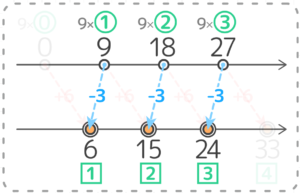
したがって番目が関係する場合は「マイナス」の考え方を使ったほうが良さそうだと分かります。
これが面倒くさい人は、等差数列の考え方を使うとスッキリします。(最終章にあります)
→マイナス型の表現か
等差数列の考え方を使う
解説
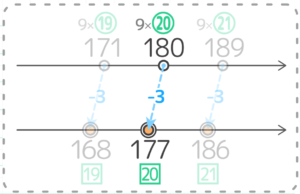
マイナス型の表現「9の倍数-3」を使います。
9の倍数の⑳番目が9×⑳=180 なので、それから3マイナスして、9×⑳-3=177と分かります
解説
この小問は番目が関係ないので易しいプラスの表現を使います。
まず1000に近い9の倍数を出します。
1000÷9=111…1 なので9×111=999 が1000付近にあります。
さらに13を足したり、引いたりして前後も出しておくと990,999,1008 が1000のそばにあります。
それらの3つ数に6プラスして1000のそばにある「9で割ると6余る数」を出すと、990+6=996(X)、999+6=1005(Y)、1008+6=1014(Z) の3つになります。
この中で、XとYが1000の前後にありますね。
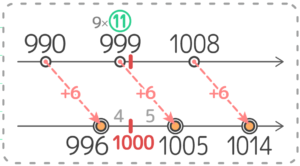
そこで、XとYのどちらが1000に近いのか差をとって比べる(大きい方-小さい方)と、
1005-1000=5 と1000-996-4 で1000に近い996 が答えになります。
別解
数直線上に倍数を表すと見やすいのですが、正確に書くのは小学生には難しい場合もあります。
そこで、表を使う方法も示します。(算数が苦手な生徒さんは、まずこちらの方法で答えを出せるようにするが優先です。)
上段に9の倍数を書き、下段に+6した数を書きます。
| 9の倍数 | 9×① 9 |
9×② 18 |
… | 9×⑩ 90 |
9×⑪ 99 |
9×⑫ 108 |
| 〃 +6 | 9+6 15 |
18+6 24 |
… | 90+6 96 |
99+6 105 |
108+6 114 |
上段では⑪番目が100に一番近いのですが、下段では⑩番目+6が一番近いのが分かります。
解説(表を使用)
表を使った解答を先に書きます
ケタ指定の倍数の個数問題と同じように考えます。こういう公式でした。

そして、数直線ではなく表を使うとこうなります。
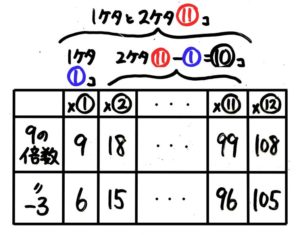
表なら簡単に書けますね
まず9の倍数を上の段に書きます。途中は省略して、1ケタから2ケタに変わる前後と2ケタから3ケタに変わる前後を書きます。
次に、-3したものを下の段に書きます。すると、1ケタと2ケタのものが⑪個、1ケタのものが①個あると分かります。
従って、2ケタのものは⑪-①=⑩個ありますね。(ここでは、植木算の番目と番差の関係を使って⑪-②+1=10でも良いでしょう)
別解(数直線)
並行する数直線を使うと、99÷9=11、9÷9=1 なので、1ケタの9の倍数は「①9」1個だけで、1ケタと2ケタの9の倍数は「⑪99」までの11個と分かります。
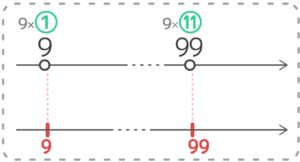
この2つの数から3を引くと、①9-3=6、⑪99-3=96
となりケタ数は変わっていません念の為、一つ後の②18-3 と⑫108-3を確かめます。これらは範囲の境目である9や99をまたいでいないので、この問題では特に考えなくてもOKでした。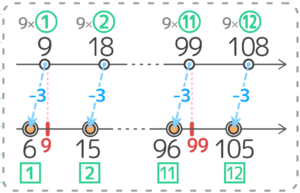 以上より、2ケタの「9で割ると6余る数」は、96までの11個から6の1個を引いて10個 と分かります。
以上より、2ケタの「9で割ると6余る数」は、96までの11個から6の1個を引いて10個 と分かります。
解き方は以上ですが、この解き方が「紛らわしい」難しい」という人も多いと思うので、もう少し単純な解き方も説明します。
それは等差数列を使った解き方です。
等差数列として解く考え方
「規則性」「等差数列」の学習が前提になります。
最低限、等差数列の公式と基本図を理解してお読み下さい。
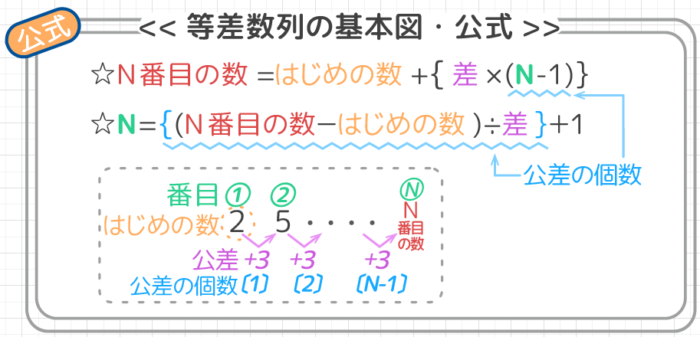
この図を見て「?」の人は関連記事「数列のまとめ」を見て下さい。
さて、倍数の第一回で、倍数=等差数列の一種 と説明しました。この「余る数」も等差数列と見ることができます。
1-2:倍数と余り(等差数列)
解説
「7で割ると3余る数」はマイナス型の表現(7の倍数-4)で考えると①3 ②10 ③17…と並んでいます。
したがって、はじめの数=3,公差=7と分かります。
「Aで割るとB余る数」を数列にすると
はじめの数:B,公差:Aの等差数列になる。
(例)7で割ると3余る数
→はじめの数:7、公差:7 の等差数列になる
解説
等差数列の基本公式「N番目の数=はじめの数+{公差×(N-1)}」を使って
30番目の数=3+{7×(30-1)}=206ですね
解説
さきほどの公式「N番目の数=はじめの数+{公差×(N-1)}」から逆算の式を作り
353=3+{7x(N-1)}
Nを求めると、N={(353-3)÷7}+1=51と分かります
解説
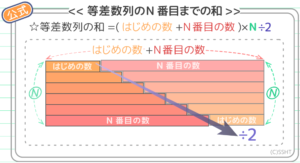
等差数列の和の公式
「数列の和=(はじめの数+N番目の数)×N÷2」に、はじめの数=3、30番目の数=206(小問2より)、N=30 をあてはめて計算すると
(3+206)×30÷2=3135 になります。
解説
はじめの数3、公差7の等差数列のN番目が300だとしてNを求めてみると…
300=3+{7×(N-1)}を逆算して、N={(300-3)÷7}+1=43.4 になります。
43.4番目の数がちょうど300になる、つまり300をギリギリ超えないのが43番目で、44番目は300を越えてしまうと分かります。
したがって、7で割ると3余る数は300までに43個あります。
このように、等差数列への直し方を憶えておけば、
「Aで割るとB余る数」を数列にすると
はじめの数:B,公差:Aの等差数列になる。
(例)7で割ると3余る数
→はじめの数:7、公差:7 の等差数列になる
悩まず簡単に解くことが出来ますね。
まとめ
「Aで割るとB余る数」
◆プラス型表現「Aの倍数+B」
◇マイナス型表現「Aの倍数ー(A-B)」
(例)7で割ると3余る数
◆プラス型の表現「7の倍数+3」
◇マイナス型の表現「7の倍数-4」

★等差数列に直す
「Aで割るとB余る数」を数列にすると
はじめの数:B,公差:Aの等差数列になる。
(例)7で割ると3余る数
→はじめの数:7、公差:7 の等差数列になる
 爽茶
爽茶→(公)約数/倍数のまとめに戻る
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ