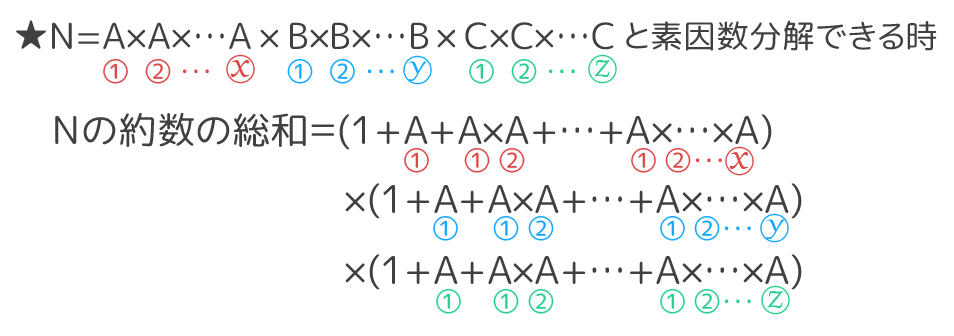約数の合計を求めたい」という方へ、東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
目次をクリックすると好きな場所に飛べます。
素因数分解から
約数の総和の求め方
(例:12の約数の総和)
素因数分解を使うと約数全部の合計(総和と言います)も分かってしまいます!!すごいですね
o(･∀･)o
中学受験には余り出題されませんが、せっかくなのでｗ紹介しましょう
[su_spoiler title=”説明を読む” style=”fancy” icon=”chevron-circle” class=”std no-trn green”]
合計の式を変形する
12の約数の合計をだしてみます。
先程の表をもう一回見ましょう。
| 2の要素(→) 3の要素(↓) |
1 | 2 | 2×2 |
| 1 | 1×1＝1 | 1×2＝2 | 1×2×2＝4 |
| 3 | 3×1＝3 | 3×2＝6 | 3×2×2＝12 |
この表を使って、
12の約数の合計を
1+2+4+3+6+12=
(1×1)+(1×2)+(1×2×2)+(3×1)+(3×2)+(3×2×2)
と直すことができます。
この式は、さらに
(1+2+2×2)×(1+3)
と直せます。
前のカッコの中は表のヨコと後ろのカッコの中は表のタテと
同じになっています！
最後の変形は小学生には理解が難しいと思うので、今回は「へ～そうなんだ」と思って下さい。
(^_^;)[/su_spoiler]
公式化
このように、素因数分解から約数の総和が求められるので
公式を示すと、
こうなりますが…分かりづらいですね
(これは、しょうがない)
実際の問題で練習しましょう
(^_^;)
類題2
(1)100 (2)126 (3)1050
小問1
100を素因数分解すると2×2×5×5 になります
「2」と「5」が使われているので、「2」と「5」のパターンをカッコに入れてかけ合わせます
「2」のパターンは「1」「2」「2×2」(1が入るのを忘れずに！！)
「5」のパターンは「1」「5」「5×5」
これらをカッコに入れてかけ算にすると
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
(1+2+2×2)×(1+5+5×5) となります。
あとは、カッコの中を計算して…
=(1+2+4)×(1+5+25)=7×31＝216です
答: 216
[/su_spoiler]
小問2
216を素因数分解すると2×3×3×7
今度は「2」「3」「7」のパターンをカッコに入れてかけ合わせます
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
「2」のパターンは「1」「2」
「3」のパターンは「1」「3」「3×3」
さらに「7」のパターンは「1」「7」
これらをカッコに入れてかけ算にすると
(1+2)×(1+3+3×3)×(1+7)
あとは計算です
=(1+2)×(1+3+9)×(1+7)=3×13×8＝312 ですね
答: 312
[/su_spoiler]
小問3
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
1050を素因数分解すると2×3×5×5×7
「2」のパターンは「1」「2」
「3」のパターンは「1」「3」
「5」のパターンは「1」「5」「5×5」
「7」のパターンは「1」「7」
これらをカッコに入れてかけ算にすると
(1+2)×(1+3)×(1+5+5×5)×(1+7)
計算して
=(1+2)×(1+3)×(1+5+25)×(1+7)=3×4×31×8＝2976です
答: 2976
[/su_spoiler]
爽茶次のステップへ
爽茶