「倍数」を学んでいる・得意になりたい中学受験生の方、例えば「3の倍数」を割り算をせずに見分けられますか？
2・3・5などの倍数かどうかをパッと見ただけで見分けられると「分数」や「場合の数」など数の分野の問題がラクに解けるようになりますよ
この記事では東大卒講師歴20年超の図解講師「そうちゃ」が2・3・5・6などの倍数の簡単な見分け方を分かりやすく図解します♪。
クイズ大会のつもりで楽しく学んで下さい。
いきなりまとめ
早く知りたい！という方、まとめをどうぞ。
倍数の見分け方には2つのタイプ(ある位を見るタイプと各位の和を見るタイプ)があるのを頭に入れて下さい。
大きく分けて2タイプあります。
●→ある位を見るタイプ
●→各位の和を見るタイプ
●2の倍数(偶数)かどうか見分ける
→1の位が0,2,4,6,8のどれか
●3の倍数かどうか
→各位の和が3の倍数
●4の倍数かどうか
→下2ケタが「00」か4の倍数
●5の倍数かどうか→1の位が0か5
●6の倍数かどうか(2段階で見分ける)
・→1の位が0,2,4,6,8のどれかで、各位の和が3の倍数
●8の倍数かどうか→下3ケタが8の倍数
●9の倍数かどうか→各位の和が9の倍数
●10の倍数かどうか→1の位が0
●11の倍数かどうか→交互の位の和の差が11の倍数か0
問題を解きたい人は、先に進んで下さい。
倍数を見分けられるとオトク
こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
今までは倍数の「もとになる数」から倍数を求めてきました。
今回は、反対に「もとになる数」を聞いていきます。例えば、こういう問題です。
例題1-1
これが「倍数かどうか」を見分ける問題です。
1回目の「倍数の意味」で説明した通り、「Aの倍数」＝「Aで割り切れる数」ですから、6で割り切れれば6の倍数ということです。
「BがAの倍数」
→①BはAを2倍・3倍…したもの
→②BはAで割り切れる
実際に90÷6を筆算してみると…
筆算
6)90
67
30
30
20
割り切れた
と割り切れるので、90は6の倍数です！
答: 倍数です
では…これはどうでしょうか
例題1-2
1111110って…
( ﾟдﾟ) ﾎﾟｶｰﾝ
もちろん、1111110÷6を筆算して割り切れるか確かめればいいんですが…面倒くさい！(よね？)
ここで！使えるワザが「倍数の識別法」というわけです。
ちなみにこの問題は、各位の和が(ゴニョゴニョ)で1の位が(ゴニョゴニョ)なので6の倍数だと3秒で！分かってしまいます。
一方…筆算では
[su_spoiler title=”筆算してみます…” style=”fancy” icon=”chevron-circle” class=”std iln no-trn pale”]
筆算すると…
6)1111110
670000
1510000
480000
231000
30000
01100
600
0510
480
030
30
00
割り切れました！
うわ～長い…3秒では無理！
(・ω・;)
というか、webで筆算を表現するのは大変なんです…
(つд`o)[/su_spoiler]
このように、倍数の識別法を知っているのといないのとでは圧倒的な差があるんです！
受験するお子さんはもちろん覚えないとダメですが…分数の約分でも使いますので受験しないお子さんも、是非覚えるのをおすすめします！
では、そんなラクチンな識別法を順に見ていきましょう！
２の倍数の見分け方
見分け方=一の位
2の倍数の識別は、知っている人も多いでしょう。
一の位(「下1ケタ」とも言います)が偶数(2,4,6,8)または「０」なら、残りがどんな数字でも２で割り切れます！
１の位が0,2,4,6,8のどれかになっている
例えば「128」は、1の位が「８」なので２の倍数です。
一方、「159」は1の位が「9」なので２の倍数ではありません
この識別法を使えば「1234567890」という長い数も、1の位が「０」なので2の倍数である、と一瞬で分かる訳ですね！
中学生への説明はこうです。
「abc」=100a+10b+c=2(50a+5b)+c よってcが２の倍数2nなら
「abc」=2(50a+5b+n)と変形できるので２の倍数である。
小学校では文字式を習わないので分からなくてもOKです！
今日は、そういうものなんだと納得して下さい。
(*^ーﾟ)ｂ
[su_spoiler title=”納得できない人に向けて(長いです)” style=”fancy” icon=”chevron-circle” class=”std no-trn green”]
え？納得できない？
(^_^;)
(ここで
webを軽く探してみると、説明しているサイトが見つからず、俄然やる気が出てきましたｗ)
では小学生向けに説明してみましょう…
３ケタの数、例えば「555」を考えてみます。
これを
100円玉5枚
10円玉5枚
1円玉5枚
のコインで持っているとします。
そして「２の倍数」＝「２で割り切れる」＝「ちょうど2つに分けられる」ですから
先程の555円分のコイン15枚を2つに分けられるか種類別に考えます。
まず100円玉5枚の500円です。
100円玉1つは50円玉２つに分けられる(両替)ので
100円が5枚あったら２つに分ける(両替)作業を5回すればOKで
100円玉が何枚あっても、同じように２つずつに分けられますね。
つまり、100の位はどんな数字がきても２つに分けられるのです。
次に10円玉5枚の50円です。
これも同じように、10円玉１つは5円玉２つに分けられ(両替)るので
10円玉が何枚あっても、同じように2つずつに分けられます。
つまり、10の位もどんな数字がきても２つに分けられるのです。
最後に1円玉5枚の5円。これは無理ですね。
100円や10円の場合と違って、1円玉はこれ以上細かくできないので、2枚を1枚ずつに分けるように、1円玉の個数で2つに分けるしかありません。
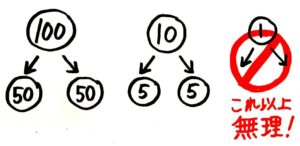
1円玉だけは2つに分けられない
そして、2つに分けられる個数は「２枚」「４枚」「６枚」「８枚」で「０枚」のときも分ける必要が無いので大丈夫です。
(この0,2,4,6,8が２の倍数になる条件ですね！)
結局、100の位(100円玉の個数)と10の位(10円玉の個数)は何でもよくて、1の位(1円玉の個数)が2,4,6,8,0ならOKということです。
並べてみました
こうして、2の倍数かどうかは、1の位だけで判断できるんですね。
(*^ーﾟ)ｂ[/su_spoiler]
では、この識別法を使った例題を解いてみましょう
類題2-1
(1)1524 (2)550001 (3)5987450
公式を使う練習です。
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
(1)１の位が「４」なので2の倍数ですね
(2)１の位が「１」なので２の倍数ではありませんね
(3)１の位が「０」なので２の倍数ですね
答: (1)ある (2)ない (3)ある
[/su_spoiler]
今度は少し考える必要がありますが、クイズだと思って解いて下さい♪
類題2-2
「3●25◯」が2の倍数になる時
●と○を求めなさい。
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
まず、使われていない数字は「1」と「4」なので、●と○は１と４と分かります。
そして、２の倍数になるということは１の位にある○は偶数なので「４」に決定します。
したがって、●は残った「１」になります。●は１，○は４、が答えになります。
作った数は「31254」だったのですね
答: ●１ ○４
[/su_spoiler]
これで、２の倍数を見分けられるようになりました！
次は3の倍数です
３の倍数の見分け方
見分け方＝各位の和
3の倍数はさっきの２の倍数とは全く違うルールです。
すべてのケタの数字を合計した数(「各位の和」)が3の倍数になっていれば、もとの数字も3の倍数になります。
例えば「123」の場合「各位の和」は 1+2+3=6 になります。
そして「各位の和」６が3の倍数なので、もとの数「123」も3の倍数だと分かるのです！
一方、「214」の場合「各位の和」が 2+1+4=7 で３の倍数でないので「214」も3の倍数ではありません
各位の和が３の倍数になっている
何故そうなるのかは、先ほどと同じように中学生になれば分かりますので、今日は納得して下さい
m(_ _)m
では、問題を解いてみましょう！
類題3-1
(1)「830」 (2)「12345」 (3)「1001001」
公式の練習ですね
[su_spoiler title=”解説と解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
(1)各位の和は 8+3+0=11 で3の倍数ではありません。よって、830自体も3の倍数ではありません。
(2)各位の和は 1+2+3+4+5=15 で３の倍数なので、元の「12345」も３の倍数です
(3)各位の和が 1+0+0+1+0+0+1=3 で３の倍数なので、元の「1001001」も３の倍数です
答: (1)ない (2)ある (3)ある
[/su_spoiler]
次が本番です。
類題3-1
「2●4」が３の倍数になる時、●は何ですか？また、その場合「24●」は3の倍数になりますか？
[su_spoiler title=”解説と解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
「2●4」が３の倍数になるということは、各位の和である 「2+●+4」 が3の倍数になるということですね。
そこで、使っていない「1」「3」「5」を●に入れて3の倍数になるか確かめます。
「1」→2+1+4＝7(X)
「3」→2+3+4＝9(O)
「5」→2+5+4＝10(X)
これで、●に入るのは３と分かります
また、「24●」つまり「243」も2+4+3=9 で各位の和は変わらないので３の倍数である、と分かります。
答: ●=3 、ある
[/su_spoiler]
「場合の数」でよく使う性質なので覚えておきましょう。
これで、３の倍数を見分けられるようになりました♪
４の倍数の見分け方
見分け方=下2ケタ
２の倍数の見分け方と似ています。
10の位と１の位(「下２ケタ」といいます。)を２ケタの数字と見て
それが「00」または４の倍数ならもとの数も４の倍数です。
数字の後ろの方だけで判断できるところが２の倍数と似ていますよね？
例えば、
「3724」の場合
下２ケタは「24」です。
そして24は４の倍数なので
もとの数「3724」も４の倍数になります。
一方
「2437」の場合
下２ケタは「37」で４の倍数ではないので
「2437」そのものも４の倍数ではありません。
(注意)
4の倍数は、同時に2の倍数でもあります。
ですから
「2437」の「７」ように
下1ケタが偶数や０でない場合はそもそも２の倍数でないので
下２ケタが４の倍数かどうかをチェックするまでもなく、４の倍数ではない、と判断できます。
下２ケタが「00」または４の倍数である
(当然、一の位は偶数)
では、
問題を解いてみましょう
類題4-1
(1)1832 (2)98765492 (3)544861754600
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
(1)1832の下2ケタは「32」で4の倍数です。
したがって「1832」自体も4の倍数です。
(2)98765432の下２ケタは「92」で4の倍数なので
「98765492」も4の倍数です。
(3)544861754600の下2ケタは「00」なので
「544861754600」自体も4の倍数です。
答: (1)ある (2)ある (3)ある
[/su_spoiler]
簡単ですね？
では、
少し頭を使う問題です
類題4-2
「◆◇●2○」が4の倍数になるような最も大きな数字は何か？
4の倍数＝下2ケタが４の倍数になる→「2○」が4の倍数になるということですね。
残った数「1」「3」「4」「5」を○の代わりに入れて「2○」が4の倍数になるになるか確かめると
[su_spoiler title=”どうなりますか？” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
４だけが、下2ケタが「24」になって４の倍数になります。したがって○＝4 と分かります。[/su_spoiler]
次に、残った「1」「３」「５」をどのように並べるか考えます。できるだけ大きい数字にしたいです。
[su_spoiler title=”どのように並べますか？” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
大きい順に「5」「3」「1」と並べればよいですね。
これで「53124」が答えと分かりました。
答: 53124
[/su_spoiler]
これで
4の倍数も見分けられるようになりました。
５の倍数の見分け方
見分け方=一の位
これは皆さんご存知でしょう。九九の五の段を連想すれば分かりますね。１の位が「0」か「5」ならその数は５の倍数です
１の位が「0」か「5」である
問題を解いてみましょう
類題5
一番小さい５の倍数は何ですか？
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
5の倍数なので、一の位に使えるのは「0」か「5」
「０」を一の位に使うと、残りの数字は「2」「7」「5」
できるだけ小さい数を作るには、残った数字を小さい順に並べればよいので
「2750」になる
「５」を一の位に使うと、残りの数字は「0」「2」「7」
残った数字を小さい順に並べるが、「0275」は3ケタの数字なのでNG!
代わりに「2」を先頭に出して「2075」になる。
「2750」と「2075」を比べると「2075」が小さいので、こちらが答えになる。
答: 2075[/su_spoiler]
これで5の倍数もOKですね。
「割り算せずに9の倍数か見分けたい」「8で割れるかどうやって見分けるの？」という小学生・中学生と保護者の方へ。この記事は前回に引き続き「倍数の識別・見分け方」を分かりやすく図解します。読み終わる頃には倍数の識別がサッとできるようになりますよ！
なお記事の最後でプリントが自由にダウンロードできますので、ぜひご利用下さい。
６の倍数の見分け方
こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
やっと、前回の一番最初にやってみせた問題『「1111110」は6の倍数ですか？』の種明かしです。
見分け方=2つの組み合わせ
6の見分け方は少し複雑で、二段階のテストをします。
６＝2✕3 と直せます(分解できます)ので、2の倍数であり３の倍数でもあります。
したがって、2の倍数になる条件(1の位が０か偶数)と3の倍数になる条件(各位の和が3の倍数)の両方をクリアしないといけません。
例題で確認しましょう
例題6
(1)1752 (2)1354 (3)1653
小問1
まず、第一条件をクリアするか確かめます。
1752は2の倍数ですか？
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
１の位が偶数なので、２の倍数です(第一条件クリア)[/su_spoiler]
↓
次に第二条件です。1752は３の倍数ですか？
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
各位の和も 1+7+5+2=15で３の倍数になっているので
1752は３の倍数です(第二条件もクリア)[/su_spoiler]
↓
結局、1752は6の倍数ですか？
[su_spoiler title=”解説と解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
２つの条件を見事クリアしたので「1752」は6の倍数です！
答(1): ある
[/su_spoiler]
小問2も同じように2段階で確かめましょう
小問2
まず、第一条件。1354は2の倍数ですか？
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
1の位は偶数で第一条件はクリアです。[/su_spoiler]
次に、第二条件。1354は3の倍数ですか？
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
各位の和が1+3+5+4=13 で3の倍数になっていないので第二条件をクリアできず[/su_spoiler]
結局、1354は6の倍数ですか？
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
第一条件はクリアできましたが第二条件をクリアできなかったので、６の倍数ではありません。残念！
答(2): ない
[/su_spoiler]
小問３も同様に確かめます。
小問3
1653は2つの条件を満たしますか？
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
「1653」は１の位が「3」で偶数ではないので第一条件をクリアできず
各位の和を調べるまでもなく６の倍数ではありません
(ちなみに各位の和は3の倍数になっています)
答(3): ない
[/su_spoiler]
2つの条件の確かめ方が分かりましたか？
1の位が「０」か偶数(2,4,6,8)で
各位の和が3の倍数
では、類題で練習して下さい。
類題6-1
(1)894 (2)6237 (3)43210
[su_spoiler title=”(1)894 の解説を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
１の位が「４」なので第一条件クリア
各位の和が8+9+4=21で３の倍数になっているので第二条件もクリアで、6の倍数です
答(1): ある
[/su_spoiler]
[su_spoiler title=”(2)6137 の解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
１の位が「7」なので第一条件をクリアできず！
第二条件を調べるまでもなく6の倍数ではありません
答(2): ない
ちなみに、各位の和も17で第二条件もクリアできません…
[/su_spoiler]
[su_spoiler title=”(3)43210 の解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
１の位が「０」なので第一条件クリア
ですが…
各位の和は0+1+2+3+4=10で３の倍数になっていないので、第二条件はクリアできず。6の倍数ではありません
答(3): ない
[/su_spoiler]
できましたか？
では、前回の記事冒頭の問題に再登場してもらいましょう♪
類題6-2
今なら、瞬時に分かりますね
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
まず、１の位は０なので第一条件クリア
次に、各位の和は1が6個なので６で3の倍数なので第二条件もクリア！
1111110は６の倍数ですね
答(3): ある
[/su_spoiler]
この6の倍数の考え方(二段階テスト)は例えば30の倍数か？というような大きな数の倍数かどうかを判断するのにも使えるので、覚えておきましょう
７の倍数の見分け方
識別法はありますが、複雑な上に、使用するシーンがないので
覚えなくても良いでしょう。
その変わり７の倍数で２ケタのものは、九九(70)以降も覚えておきましょう。
「70」「77」「84」「98」です。
８の倍数の見分け方
見分け方=下3ケタ
2の倍数・4の倍数に似ています。
下3ケタが８の倍数なら、元の数自体も8の倍数になります。一応、覚えておきましょう。
類題8
９の倍数の見分け方
見分け方
3の倍数とよく似ています。
各位の和が9の倍数なら元の数も９の倍数になります。
例えば、「15192」は各位の和が1+5+1+9+2=18 で9の倍数になっているので「15192」自体も9の倍数です
一方、「37564」は各位の和が3+7+5+6+4=25 で９の倍数になっていないので「37564」自体も９の倍数ではありません
各位の和が9の倍数になっている
では、類題で練習して下さい
類題9-1
(1)「308」 (2)「42732」 (3)「3003003003」
公式の練習ですね
[su_spoiler title=”(1)「308 」の解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
各位の和は3+0+8=11 で9の倍数でないので、308自体も9の倍数ではありません。
答(1): ない
[/su_spoiler]
[su_spoiler title=”(2)「42732」 の解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
各位の和は 4+2+7+3+2=18 で9の倍数なので、元の「42732」も9の倍数です
答(2): ある
[/su_spoiler]
[su_spoiler title=”(3)「3003003003」 の解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
各位の和が 3+3+3+3=12 で9の倍数ではないので、元の「3003003003」も９の倍数ではありません
答(3): ない
[/su_spoiler]
これで9の倍数も見分けられるようになりましたね！
10の倍数の見分け方
見分け方
当然ご存知と思いますが、1の位が「０」なら10の倍数ですね。
何故そうなるか、もう分かるのではないでしょうか
そうです。
10=2×5 なので
2の倍数の条件(一の位が0か偶数)と5の倍数の条件(一の位が0か5)の
2つの条件を満たさないといけません。
そして、それは「一の位が0」の場合だけだからですね！
類題
11の倍数の見分け方
見分け方
急いで覚える必要はありませんが、簡単で面白いので覚えてしまいましょ♪
見分け方は「ある数の位を交互に合計した2数の差が『11の倍数』か『０』なら、もとの数も11の倍数」です
例題で試してみましょう
X-1:(サブタイトル)
ヒント
位を交互に足すので→ 一の位+百の位 と 十の位+千の位 の差が11の倍数か0なら11の倍数です
解説
1628を位を交互に合計します
１の位(8)と100の位(6)の和が8+6=14
10の位(2)と1000の位(1)の和が2+1=3
その差は14-3=11で11の倍数になっている！ので「1628」自体も11の倍数です。
解説
2024の位を交互に合計します
１の位(4)と100の位(0)の和は4、10の位(2)と1000の位(2)の和も4で、差は4-4=0になるので「2024」自体も11の倍数です
ちなみに2024=8x11x23 です
解説
の位を交互に合計します80927
１の位(7)と100の位(9)と10000の位(8)の和は24、10の位(2)と1000の位(0)の和2で、差は24-2=22 で11の倍数になっているので「80927」自体も11の倍数です。
分かりましたね？
→各位を交互に足した数の差が「11の倍数」か「0」
例「80927」
→１の位(7)と100の位(9)と10000の位(8)の和は24
10の位(2)と1000の位(0)の和は2
差は24–2=22 で11の倍数
→「80927」自体も11の倍数
例「2024」
→１の位(4)と100の位(0)の和は4
10の位(2)と1000の位(2)の和も4
差は4–4=0
→「2024」自体も11の倍数
利用問題
頭の体操的に1問どうぞ
X-1:11の倍数の識別
「◆●1◇」が44の倍数になる時、◆●◇にあたる数字は何ですか？
ヒント
44＝4×11 と分解できるので…
解説
まず、44＝4×11 と分解できるので、できた数は4の倍数のはず
4の倍数は下2ケタが4の倍数になるので、できた数の下2ケタ「1◇」も4の倍数になり、◇=1,2,3,4のいずれかなので、◇＝2 と分かる。
また、できた数は11の倍数でもあるから、互い違いのケタの和、つまり「◆+1」と「●+◇」の差が11の倍数か0になるはず。
◇＝2なので、交互の位の合計は「◆+1」と「●+2」になり、◆と●は3と4なので差は最大でも3+1と4＋2の差の2にしかならない(11の倍数にはならない)ので、11の倍数になるのは差が0つまり◆+1＝●+2 の場合のみと分かる。
その条件を満たすのは ◆＝4、●＝3 と分かる。できる数は「4312」
以上で倍数の見分け方は全て終了です。お疲れ様でした！
倍数の見分け方のまとめ
もう一度まとめると、こうなります。
大きく分けて2タイプあります。
●→ある位を見るタイプ
●→各位の和を見るタイプ
●2の倍数(偶数)かどうか見分ける
→1の位が0,2,4,6,8のどれか
●3の倍数かどうか
→各位の和が3の倍数
●4の倍数かどうか
→下2ケタが「00」か4の倍数
●5の倍数かどうか→1の位が0か5
●6の倍数かどうか(2段階で見分ける)
・→1の位が0,2,4,6,8のどれかで、各位の和が3の倍数
●8の倍数かどうか→下3ケタが8の倍数
●9の倍数かどうか→各位の和が9の倍数
●10の倍数かどうか→1の位が0
●11の倍数かどうか→交互の位の和の差が11の倍数か0
今日からはこの「識別法」を使って
いろんな数字を観察すると面白いかもしれませんね。
プリントダウンロート
画像をクリックするとプリントが表示されますので保存して下さい。
メアド等の入力は必要ありませんが、著作権は放棄しておりません。無断転載引用はご遠慮ください。
このプリントは旧版です。現在改訂作業中です(2020/1/9)
次のステップへ
爽茶→(公)約数/倍数のまとめに戻る
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!