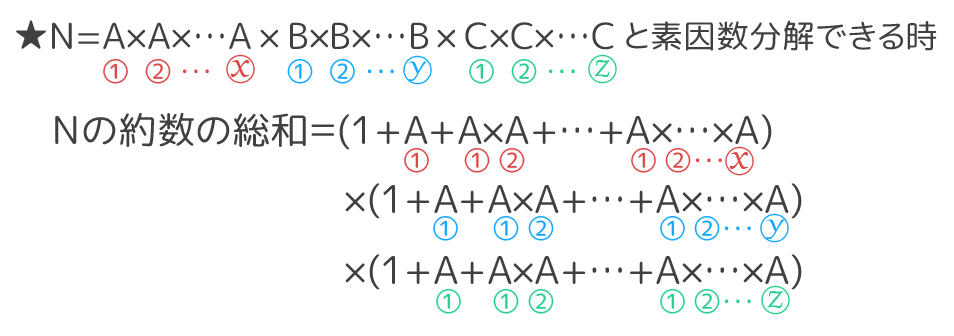●公倍数公約数の個数
●公倍数公約数と余り
●公約数公倍数の応用
文章題「平等に分配」の誤りを修正しました。混乱した方にお詫び致します
「倍数・約数・公約数・公倍数の基本から応用までマスターしたい！」という中学受験生の方、おまかせ下さい！
東大卒講師歴20年の図解講師「そうちゃ」が公倍約数の問題を分かりやすくまとめました♪
この記事を最後まで読み通すことができれば「公倍約数マスター」になれるでしょうが、非常に長いので。目次をクリックして読みたいところに飛んでも良いでしょう。各項目からはもっと細かい説明がある個別記事に飛ぶこともできます。
(公)倍数の基本事項
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
はじめは学校教科書レベルの説明です！倍数の基礎
倍数は「九九」を延長したように続いていく数
→➁AはBで割り切れる
2の倍数(と2の倍数でない数)には特別な名前が付いています。
→◆偶数…2の倍数である数
◇奇数… 〃 でない数
●見分け方
一の位が2,4,6,8,0のどれかなら偶数
「1237」→奇数
もっと基礎から詳しい説明を読みたいを解きたい人は姉妹サイト「そうちゃ式 旧館」の「倍数の基礎」を見て下さい
倍数の見分け方
分数の約分(→参考記事)をする時など、倍数をパッと見分けられると便利です。
大きく分けて2タイプあります。
●→ある位を見るタイプ
●→各位の和を見るタイプ
●2の倍数(偶数)かどうか見分ける
→1の位が0,2,4,6,8のどれか
●3の倍数かどうか
→各位の和が3の倍数
●4の倍数かどうか
→下2ケタが「00」か4の倍数
●5の倍数かどうか→1の位が0か5
●6の倍数かどうか(2段階で見分ける)
・→1の位が0,2,4,6,8のどれかで、各位の和が3の倍数
●8の倍数かどうか→下3ケタが8の倍数
●9の倍数かどうか→各位の和が9の倍数
●10の倍数かどうか→1の位が0
もっと詳しい説明を読みたい人は姉妹サイト「そうちゃ式 旧館」の「倍数の見分け方」を見て下さい
公倍数
意味
言葉の意味は「2つ以上の数に共通する倍数」ですが、他にもいろんな意味があります。一番最後が大切です。
●公倍数
＝2つ以上の数に共通する倍数
＝2つ以上の数で割り切れる数
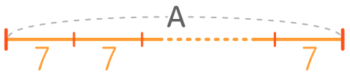
(例)6と9の公倍数
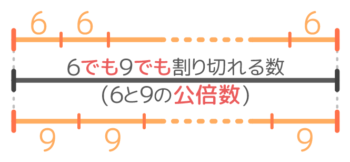
●最小公倍数＝はじめの(一番小さい)公倍数
●公倍数は最小公倍数の倍数
(例)6と9の公倍数
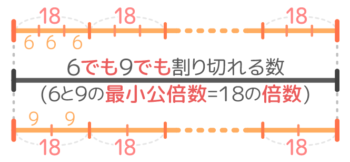
求め方
学校で習うのは「書き出し法」です。
→2つの数のうち大きい方を2倍・3倍していき、
小さい方の倍数にもなったら、それが最小公倍数。
公倍数は最小公倍数を1倍・2倍…していけば良い
小さい方の10を2倍3倍していく…
10の2倍は20。20は6の倍数ではないでないので公倍数でない。
10の3倍は30。30は6の倍数なので、これが最小公倍数。
最初の公倍数は180×1=180、2番目は60×2=120、3番目は60×3=180…
もっと基本から詳しい説明を読みたい人は姉妹サイト「そうちゃ式 旧館」の「公倍数の意味と求め方」を見て下さい
中学受験では「すだれ算」を使って最小公倍数を計算で直接出します。(→この記事の下の方で説明しています)
(公)約数の基礎
約数の基礎
約数の意味
約数はもとの数を割って(分解して)できる数です。
「AがBの約数」
→❶B=A×○と分解できる。
→❷AはBを割り切れる
12＝2×6と分解できるし
12÷2=6 と割り切れる
求め方(書き出し)
無限に続く倍数と違い、約数には限りがあります。まずは書き出しで求められるようにします。
→X=A×B＝C×D…と分解できる時、
A,B,C,D(,E,F)はXの約数である。
12=1×12=2×6=3×4と分解できるので
12の約数は1,2,3,4,6,12
実際に求めて下さい！
20の約数を全て書き出しなさい
→( 20=1×20=2×10=4×5なので 1,2,4,5,10,20 )
もっと基礎から詳しい説明を読みたい人は姉妹サイト「そうちゃ式 旧館」の「約数の基礎」を見て下さい
公約数
意味
言葉の意味としては「2つ以上の数に共通する約数」ですが、他にも意味があります。最後のものが重要です。
＝2つ以上の数に共通する約数
＝2つ以上の数を割り切れる数
●最大公約数＝一番大きい公約数
●公約数は最大公約数の約数
実はもう一つ「公約数=2数の差の約数」という考え方があります(受験小5以降)。こちらで説明しています。
求め方
→2つの数のうち小さい方の約数を「書き出し」
で求め、その中で大きい方の約数にも
なっている数が公約数。
その中で一番大きなものが最大公約数
(公約数はみな最大公約数の約数になっている)
小さい方12の約数は1,2,3,4,6,12で、このうち
16の約数になっている(割り切れる)のは1,2,4なので
公約数は1,2,4と分かる
確認テストをどうぞ
12と18の公約数を求めなさい
→( 12の約数は1,2,3,4,6,12で18の約数は1,2,3,6,9,18なので、共通する約数は1,2,3,6 )
12と18の公約数はどのような数か？一言で表現しなさい
→( 12と18の最大公約数が6なので、12と18の公約数は6の約数 )
もっと基礎から詳しい説明を読みたい人は姉妹サイト「そうちゃ式 旧館」の「公約数の意味と求め方」を見て下さい。
中学受験では最大公約数を「すだれ算」を使って計算で出します(→この記事の下の方で説明しています)
公約数の応用問題
(例題1)
A,B,Cが1でない整数で
AxB=12
AxC=18
の関係にあるとき、考えられるA,B,Cの組み合わせを全て答えよ
Aは12と18両方の約数なので12と18の公約数。
公約数は最大公約数の約数で、12と18の最大公約数は6だから、12と18の公約数は6の約数の1,2,3,6
Aは1でないので、2,3,6のいずれかと分かる
A=2の場合、B=12÷2=6、C=18÷2＝9
A=3の場合、B=12÷3=4、C=18÷3＝6
A=6の場合、B=12÷6=2、C=18÷6＝3
以上より(A,B,C)=(2,6,9),(3,4,6),(6,2,3)
(例題2)
A,B,C,Dが1でない整数で
AxB=30
AxC=75
AxD=105
の関係にあるとき、考えられるA,B,C,Dの組み合わせを全て答えよ
Aは30,75,105の約数なので30と75と105の公約数。
公約数は最大公約数の約数で、30と75と105の最大公約数は15(30の約数1,2,3,5,6,10,15,30のうち大きい方から75と105両方を割り切れるか確かめていく)だから、30と75と105の公約数は15の約数の1,3,5,15だが、Aは1でないので、3,5,15のいずれかと分かる
A=3の場合、B=30÷3=10、C=75÷3＝25、D=105÷3＝35
A=5の場合、B=30÷5=6、C=75÷5＝15、D=105÷5＝21
A=15の場合、B=30÷15=2、C=75÷15＝5、D=105÷15＝7
以上より(A,B,C,D)=(3,10,25,35),(5,6,15,21),(15,2,5,7)
最後は少し面倒でしたね…
ここまでが小学校範囲の問題でした。次からは中学受験の内容です
範囲と(公)倍数(中学受験)
爽茶～に一番近い倍数
問題文の指定方法に注意します。
●Nより小さいAの倍数で、Nに一番近い数
→A×(N÷A) *わり算の余りは無視
→6×(100÷6)=6×16=96
●Aの倍数のうち、一番Nに近い数
→A×(N÷A) と A×(N÷A)+A を比べる *わり算の余りは無視
→6×(100÷6)=96 と 96+6=102 を比べて、102が答え。
確認テストをどうぞ
200より小さい7の倍数で一番200に近いのは何か？
→( 7×(200÷7)=7×28=196 )
7の倍数で一番200に近いのは何か？
→( 196 と 196+6 を比べる。196と203を比べて203 )
くわしい説明を読みたい・もっと問題を解きたい人は本サイトの「範囲と(公)倍数」を見て下さい
素因数分解と約数(すだれ算)
応用問題を解くには「素因数分解」を使います
素数
「1×その数」にしか出来ない数を「素数(そすう)」という。
→「1×その数」という形にしか分解できない数
(例) 2→素数、3→素数
6→違う(2×3に分解できる)
1→違う(分解できない)
●よく使う基本的な素数
→2,3,5,7…
確認テストをどうぞ
7は素数ですか？→( 1×7にしか分解できないのでO )
9は 〃 ？→( 1×9以外にも3×3と分解できるのでX )
11は 〃 ？→( 1×11にしか分解できないのでO )
53は 〃 ？→( 1×53にしか分解できないのでO )
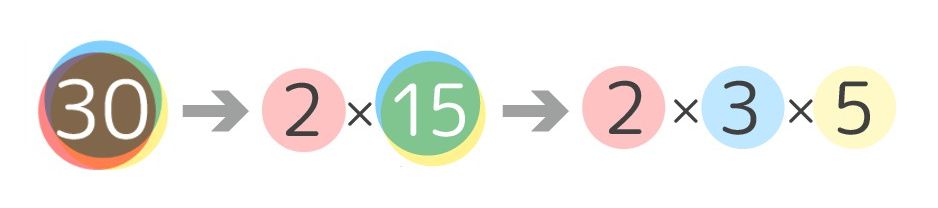
素因数分解のやり方
2つのやり方があります。
ニ分解式
2つの数のかけ算にどんどん分解する方法。
→素数になるまでどんどん分解する方法
60=6×10=2×3×2×5
=2×2×3×5←小さい順に並べ直して完成
すだれ算
「答えを下に書いていく割り算」すだれ算で分解する方法。小さい素数で割っていく。
確認テスト
(2021.7.29作成中)
詳しい説明を読みたい・問題を解きたい人は「すだれ算と素因数分解のやり方」を見て下さい。
素因数分解を使った応用問題
約数の個数を素因数分解から求める
→この先「約数の個数」で解説(解説へジャンプ)
素因数分解の構成を考える問題
素因数分解した時の、素数の種類と個数を使ったパズルのような問題。
→素因数に分解して素数の種類別の個数に注目
(例)A×600=B×B×B を成り立たせる最小のB
→600を素因数分解すると2×2×2×3×5×5なので、A×600=A×2×2×2×3×5×5 になる。
→これをB×B×Bの形にするには(2×3×5)×(2×3×5)×(2×3×5)にする必要があるので
最小のB=(2×3×5)=30 と分かる
確認テストをどうぞ
(2021.7.29作成中)
詳しい説明を読みたい人は関連記事「素因数分解の応用問題」を見て下さい
割り切れる回数を求める
ある大きな数を小さな素数で割っていくと、何回割り切れるかという問題
ある数Nを素数Aで割り切れる回数
=Nを素因数分解した時のAの個数
6=2×3 →1回
7(素数) →0回
8=2×2×2 →3回
1680=2×2×2×2×3×5×7 →4回
少し複雑にした問題
●ある数Nを素数A×素数B(A<B)で
割り切れる回数
=Nを素因数分解した時の
AとBの少ない方の個数
6=2×3
2520=2×2×2×3×3×5×7 で、
2と3では3が少ない →2回
確認テスト
(2021.7.29作成中)
詳しい説明を読みたい人は関連記事「素因数分解の応用問題」を見て下さい
末尾の0の個数を求める
大きさを直接書かずに「1×2×3×4×5…」のようにかけ算で示された数の末尾に0がいくつ並ぶか聞かれる問題
→10で割り切れる回数と等しい
10=2×5なので、
素因数分解して2と5の少ない方の個数
→5の方が少ないので5がいくつあるか調べる
(50÷5)+(50÷25)=12個
確認テスト
詳しい説明を読みたい人は関連記事「素因数分解の応用問題」を見て下さい
素因数分解と公約数・公倍数
「公約数は最大公約数の約数」で「公倍数は最小公倍数の倍数」でした。つまり最大公約数と最小公倍数が分かれば公約数と公倍数も分かります。
その重要な最大公約数と最小公倍数を一気に求める方法が「はしご算」です。
はしご算のやり方
2つの数のはしご算
素因数分解の「すだれ算」を2つの数で行います。2つの数に共通する素数(公約数)で割っていきます。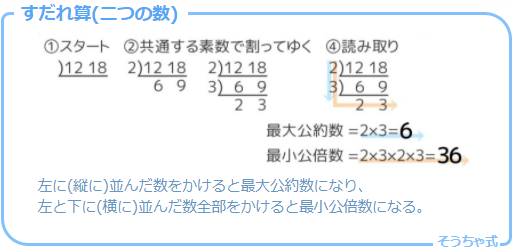
確認テストをどうぞ
45と75の最大公約数と最小公倍数をすだれ算で求めよ
→( すだれ算をすると下のようになるので、最大公約数=3×5=15、最小公倍数＝3×5×3×5=225 とわかる
最小公倍数:
3×5×3×5=255
詳しい説明を読みたい・もっと問題を解きたい人は「素因数分解(すだれ算)と公約数公倍数」を見て下さい。
3つの数のはしご算
数が3つある場合も同じように行うが、二数しか割れない素数が出てきた場合に特殊なやり方をする。
確認テストをどうぞ
90と50と210の最大公約数と最小公倍数をすだれ算で求めよ。
最小公倍数:
2×3×5×3×5×7=3150
詳しい説明を読みたい・問題を解きたい人は「三つの数のすだれ算」を見て下さい。
はしご算を利用した問題
最大公約数と最小公倍数から、もとの2数を求める問題では「簡略化したはしご算」の形を利用します。
2 3
最小公倍数は6×2×3=36
ここに現れている数の関係を公式風にすると、こうなります。
a b
(aとbは互いに素*)
最大公約数=X
最小公倍数Y=X×a×b
A=X×a、B=X×b
確認テスト
最大公約数が3で最小公倍数が84である2つ数を求めよ。ただし2つの数は共に2ケタの数である。
a b
最大公約数=3
最小公倍数84=3×a×b
4 7
最小公倍数84=3×4×7
A=3×4=12、B=3×7=21
12と21が答えと分かります。
詳しい説明を見たい人は関連記事「すだれ算と素因数分解」内の「はしご算を利用した問題」を見て下さい。
はしご算が使えない時の方法
公約数＝最大公約数の約数とおぼえたが、もう一つ、「2つの数の公約数は2つの数の差の約数」という考え方を憶えておくと良い
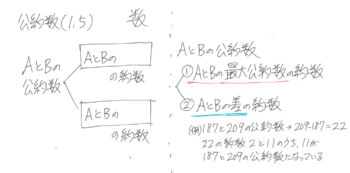
「差の約数」の考え方を使う
小まとめ
個数の問題
倍数の個数
無限に続く倍数ですが、範囲を区切れば個数が決まります。
基本公式
まず1からある数まで範囲を区切った場合の個数の出し方を覚える。
●1からNまでの間にあるAの倍数の個数
→N÷A個(余りは無視)
→100÷3=33…1→33 個
これを利用すれば、1からでない範囲内の個数も求められる。
●NからMまでの間にあるAの倍数の個数
→(M÷A)-((N-1)÷A) 個(余りは無視)
*N-1になる事に注意！
→(100÷3)-((50-1)÷3)=33-16=17個
試してみましょう♪
100から200までの間にある7の倍数の個数は？
→( (200÷7)-((100-1)÷7)=28-14=14個 )
ケタ数指定
範囲ではなく、ケタ数で区切って個数を聞かれることがよくあります。上の考え方を利用します。
●1ケタのAの倍数の個数
=1から9までの間のAの倍数の個数
→9÷A 個(余りは無視)
●2ケタのAの倍数の個数
=10から99までの間のAの倍数の個数
→(99÷A)-(9÷A) 個(余りは無視)
→(99÷7)-(9÷7)=14-1=13 個
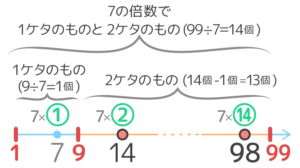
●3ケタのAの倍数の個数
=100から999までの間のAの倍数の個数
→(999÷A)-(99÷A) 個(余りは無視)
問題を試してみましょう！
4の倍数で2ケタのものは何個あるか？
→( (99÷4)-(9÷4)=24-2=22個 )
11の倍数で3ケタのものは何個あるか？
→( (999÷11)-(99÷11)=90-9=81個 )
もっとじっくり説明を読みたい人は「倍数の個数」を見て下さい。
公倍数の個数(ベン図の問題)
基本解法
公倍数は最小公倍数の倍数なので、上と同じ方法で求められる。
試しにテストしてみましょう
3と4の公倍数は1から300までの間に何個あるか？
→( 3と4の最小公倍数は12なので、12の倍数が1から300までの間に何個あるか求める )
→( 300÷12=25個 )
3と4の公倍数で200より小さく、一番200に近いものは？
→( 12の倍数で200より小さく一番200に近いものを求める )
→( 200÷12=16 12×16=192 )
3と4の公倍数で一番200に近いものは？
→( 上で出した192とその次の12の倍数204を比べて、近いのは204 )
ベン図を使った問題(二数の場合)
「ABのどちらかで割り切れる数」や「ABどちらでも割り切れない数」を求める問題です。ベン図をイメージします。
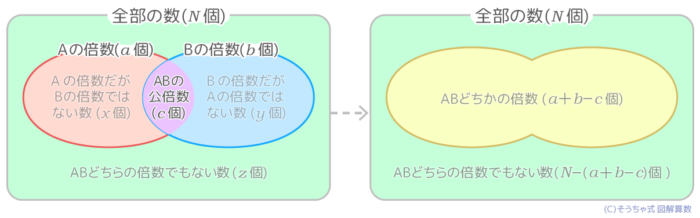右図のように条件内のすべての数の個数をN,
Aの倍数(Aで割り切れる数)の個数をa,
Bの倍数(Bで割り切れる数)の個数をb,
ABの公倍数(AでもBでも割り切れる数)の個数をc とする時
●ABどちらかの倍数(AかBで割り切れる数)の個数
=(a+b)-c *右図の「ピーナッツ」形
●ABどちらの倍数でない数(AでもBでも割り切れない数)の個数z
=N-{(a+b)-c}
この図(ベン図)が良く分からない/忘れた人は参考記事「集合算のまとめ」を見て下さい。
確認テストをどうぞ
1から100までの整数がある。
2または3で割り切れる整数は何個あるか？
→1から100までで、2で割り切れる数=2の倍数の個数は( 100÷2=50個(a) )
→同様に3で割り切れる数=( 3の倍数の個数は100÷3=33個(b) )
→2でも3でも割り切れる数=( 2と3の公倍数=6の倍数の個数は100÷6=16個(c) )
→よって2または3で割り切れる数の個数は( a+b-c=50+33-16=67個(ピーナッツ型) )
2でも3でも割り切れない整数は何個あるか？
→( 範囲内にある数(N)は全部で100個なので、N-ピーナッツ=100-67=33個 )
ケタ数も組み合わせた問題もあります。
3ケタの整数のうち、12でも18でも割り切れない数は何個あるか？
→( 3ケタの整数は全部(N)で999-99=900個。
このうち12の倍数の個数(a)は(999÷12)-(99÷12)=83-8=75個。18の倍数の個数(b)は(999÷18)-(99÷18)=55-5=50個(b)。
12と18の公倍数(c)=36の倍数の個数は )(999÷36)-(99÷36)=27-2=25個(c)。
よって12でも18でも割り切れない数の個数(N-(a+b-c))は900-(75+50-25)=800個 )
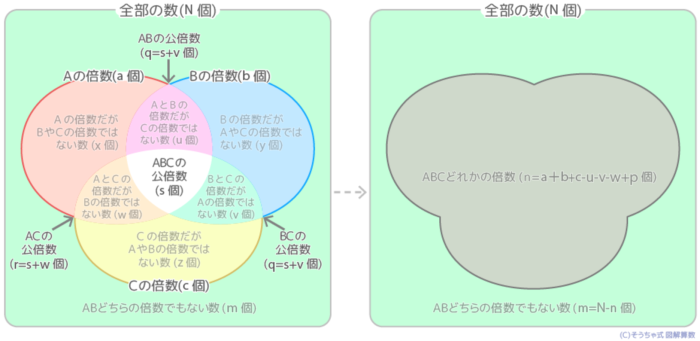
公倍数の個数(三数の場合)
「ABCどれでも割れる数」「AでもBでもCでも割れる数」や「AとBでは割れるがCでは割れない数」を求めます。
右図のように条件内のすべての数の個数をN,
Aの倍数(Aで割り切れる数)の個数をa,
Bの倍数(Bで割り切れる数)の個数をb,
Cの倍数(Cで割り切れる数)の個数をc,
ABの公倍数の個数をp,BCの公倍数の個数をq,ACの公倍数の個数をr
ABCの公倍数(AでもBでもCでも割り切れる数)の個数をsとする時
●ABCどれかの倍数(AかBかCで割り切れる数)の個数
=(a+b+c)-(p+q+r)+s *右図の「クローバー」形
これは公式を覚えなくてもa,b,c,p,q,r,sからu,v,wとx,y,zをコツコツと求めて答えが出せればOKです
●ABCどれの倍数でもない数(AでもBでもCでも割り切れない数)の個数z
=N-クローバー形の数
確認テストで実際に計算してみましょう(けっこう面倒くさいです…)
3でも4でも5でも割り切れる数(p)の個数は？
→( 3,4,5の公倍数=の3,4,5の最小公倍数60の倍数 )の個数を求めればよい
→( 1000÷60=16余り40なので、16個 )
3と4では割り切れるが5では割り切れない数(u)の個数は？
→( 3,4の公倍数の個数(p)から3,4,5の公倍数の個数(s)を引いたもの )を求めれば良い
→( 3,4の公倍数=12の倍数の個数は、1000÷12=83余り4より83個 )
→( 83-16=67個 )
3か４か５で割り切れる数は何個あるか？
→同じように、( 4と5では割り切れるが3では割り切れない数(v)、3と5では割り切れるが4では割り切れない数(w) )を求めていく
3でも4でも5でも割り切れない数は何個あるか？
→
この図(ベン図)が良く分からない/忘れた人は参考記事「集合算のまとめ」を見て下さい。
確認テスト
公倍数の個数の利用問題
約数の個数
書き出す
小さい数の約数は2つの数のかけ算に直すことで数えることができます。
●Aの約数の個数
→AをP×Qの形に直せる時、
PとQがAの約数であることを利用し
書き出して数える
12=1×12=2×6=3×4 なので
→12の約数は1,2,3,4,6,12 の6個
確認テストをどうぞ
18の約数は何個か？
→( 18=1×18=2×9=3×6 なので、1,2,3,6,9,18の6個 )
素因数分解の形から約数の個数を出す
単純に書き出す以外にも、素因数分解ができる人なら計算で求めることができます。
確認テストで試してみましょう♪
12の約数の個数を求めよ
→( 12＝2×2×3(2が❷回、3が❶回)なので、12の約数は(❷+1)×(❶+1)=2×3=6個 )
90の約数は何個あるか？
→( 90=2×3×3×5(2❶回、3❷回、5❶回)なので、90の約数は(❶+1)×(❷+1)×(❶+1)=2×3×2=12個 )
詳しい説明を読みたい、問題を解きたい人は参考記事「約数の個数」を見て下さい。
逆向きの問題
逆に約数の個数から素因数分解の形を求める問題で、公式の形を観察すれば、以下の法則があるのが分かります。
●約数が1個の数→「1」だけ
●約数が2個の数→「A」(素数:2,3,5など)
●約数が3個の数
→素因数分解すると「N x N」(素数の平方数:2×2など)
●約数が4個の数
→素因数分解すると「A×B」または「A×A×A」の形になる数
→「A×B」形は6(2×3),10(2×5),14(2×7),15(3×5)
「A×A×A」形は8(2×2×2)で、合計5個
確認テストをどうぞ
「１から50までの数のうち、約数が3つのものは何個あるか？」
→( 1から50までに1以外の素数の平方数は「4(2×2)」「9(3×3)」「25(5×5)」「49(7×7)」の5個。)
詳しい説明を読みたい、問題を解きたい人は参考記事「約数の個数」を見て下さい。
(参考)約数の総和
上の形を使うと約数の合計(総和)を求めることもできます。
確認テストをどうぞ
12の約数の総和を求めよ
→( 12=2×2×3なので、約数の総和は(1+2+2×2)×(1+3)=7×4=28 )
(書き出し式でも、1+2+3+4+6+12=28 と同じになる)
詳しくは「約数の総和」を見て下さい。
公約数の個数(ベン図の問題)
基本
公約数は最大公約数の約数なので、公約数の個数は約数の個数と同じように計算で求められる。
270と450の公約数の個数は？
→( 270と450の最大公約数は90。90=2×3×3×5なので、約数の個数は(❶+1)×(❷+1)×(❶+1)=12 )
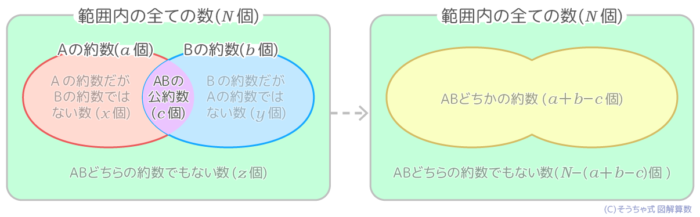
ベン図を使った問題
「aかbのどちらかを割り切れる数」を求める問題
右図のように条件内のすべての数の個数をN,
Aの約数(Aを割り切れる数)の個数をa,
Bの約数(Bを割り切れる数)の個数をb,
ABの公約数(AB両方を割り切れる数)の個数をc とする時
●ABどちらかの約数(AかBを割り切れる数)の個数
=(a+b)-c *右図の「ピーナッツ」形
●ABどちらの約数でない数(ABどちらも割り切れない数)の個数z
=N-{(a+b)-c}
確認テストをどうぞ
270か450どちらかを割り切れる数の個数は？
→( 270の約数の個数は270=2×3×3×3×5より約数は2×4×4=16個(a) )
→( 450の約数の個数は450=2×3×3×5×5より約数は2×3×3=18個(b) )
→( 270と450の公約数の個数は最大公約数90の約数で12個(c) )
→( 求める個数は(a+b)－c=(16+18)-12=22個 )
爽茶個数の問題は以上です。次は「余り」の問題です。
余りの問題
非常によく見る問題ですが、倍数の問題なのか約数の問題なのか、紛らわしいんですね。
スタート方向を間違えないのが大切。
割る問題の分類
余りが出るのは「割る」場合で、「～で割る」と「～を割る」の2つの表現があります。
この2つの表現のどちらが問題に出てきたら、倍数の問題か約数の問題かかを即座に判断できないといけません。
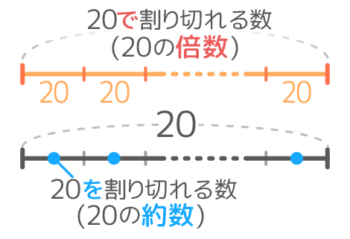
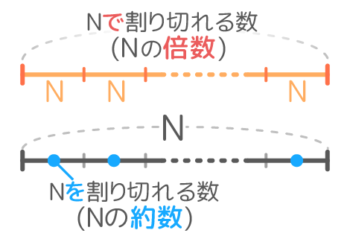
まず、余りなしで割り切れる場合、例えば「20で割り切れる数」と「20を割り切れる数」を線分図にして考えるとこうなります。
つまり、「～で割る」は倍数の問題で、「～を割る」は約数の問題になります。
●「Nで割ると…な数」→Nの倍数の問題
●「Nを割ると…な数」→Nの約数の問題
余りの問題の全体像
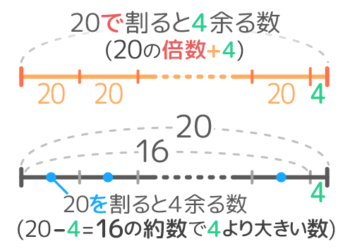
次に余りがある場合、例えば「20で割ると4余る」と「20を割ると4余る」を考えるとこうなります。
約数の問題になるときは「余りよりも大きい数」という条件を忘れないようにしましょう。
これで「余り」の問題も、どちらが倍数か約数か分かりました。
●「Nで割ると…余る数」→Nの倍数の+余り
→20の倍数+4 (または 20の倍数-16)
●「Nを割ると…余る数」
→(N－余り)の約数で余りよりも大きい数
→(20-4=)16の約数で4より大きい数
では、倍数の問題と約数の問題を順番に見ていきます。
倍数と余り
倍数を使うと「～で割ると～余る」数を簡単にあらわすことができます。
プラス型とマイナス型
プラス型「～の倍数＋○」とマイナス型「～の倍数－○」の2つの表現方法があります。
●プラス型の表現＝「Nの倍数＋A」
●マイナス型の表現=「Nの倍数-(N-A)」
例:7で割ると3余る数
→プラス型の表現=「7の倍数＋3 」
→マイナス型の表現=「7の倍数－4」
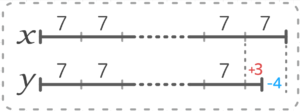
これを実際に使って個数や番目が関係する問題を解く時は等差数列に直すと簡単です。
等差数列で表す
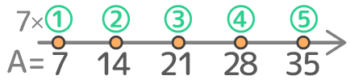
7で割って3余る数つまり「7の倍数+3」を「ゼロ番目」から小さい方から書くと、7×0+3,7×➀+3,7×➁+3…で「3,10,17…」になります。
これは「はじめの数=3,公差=7の等差数列」と同じです。はじめの数=余り(3)、公差=割る数(7)になっているのに注目！です
あとは等差数列の問題として解けます(小5以降の受験生にはこちらをすすめます)
→「はじめの数=A,公差=Nの等差数列」
→はじめの数=3,公差=7の等差数列
①3 ②10 ③17 ④24…
○番目の数・番目(N)を求める
等差数列の公式を使えば一発
N番目の数=はじめ+差×(N-1)
N={(N番目の数-はじめの数)÷差}+1
例
「近い数」を求める
7で割ると3余る数で200に一番近い数？
→
個数を求める
等差数列のN(番目)を出す式
N={(N番目の数-はじめの数)÷差}+1
を利用すれば一発で出せる
1から300までの整数のうち、7で割ると3余る数はいくつあるか？
→はじめの数3、差7の等差数列のN番目が300だとしてNを求めると、N=((300-3)÷7)+1=43.4… つまり44番目は300を越えてしまうので、300までには43個あると分かる
詳しい説明を読みたい・問題を解きたい人は「倍数と余り(～で割ると余る数)」を見て下さい。
公倍数と余り
問題文によって三つの型があります。どの型からも等差数列に直せれば簡単に扱えるようになります。
三つの一致型
「プラス一致」型
例:5で割っても7で割っても2余る数
→「5の倍数+2」と「7の倍数+2」で+2(プラス)が一致している。
よって「5と7の公倍数+2」から「35の倍数+2」というプラス型の表現ができるので「はじめの数2、差35の等差数列」と同じになる。
(一応「35の倍数-33」というマイナス型の表現もできる)
「マイナス一致」型
例:5で割ると2余り、7で割ると4余る数
→「5の倍数+2」と「7の倍数+4」なのでプラスは一致していないが、マイナス型に直すと「5の倍数-3」と「7の倍数-3」でマイナスが一致している♪
よって「5と7の公倍数－3」から「35の倍数－3 」というマイナス型の表現にでき、これをプラス型に直すと「35の倍数+32」になるので「はじめの数32,差35の等差数列」と同じになる。
「不一致」型
プラスでもマイナスでも一致しない場合、最初の一個を書き出しで求めないといけません。これが少し面倒です…
例:5で割ると2余り、7で割ると3余る数
→プラスはもちろん、マイナス表現にしても「5の倍数-3」と「7の倍数-4」で一致しないのでｗはじめの一個を書き出しで求める。
大きい方(7の倍数+3)を書き出していき、小さい方の条件(5の倍数-3)を満たすか調べていく。
①7×0+3=3(5の倍数-3ではない)
②7×1+3=10(5の倍数-3ではない)
③7×2+3=17(5の倍数-3になってる！)
はじめの数は17と分かりました。
この17からは5と7の最小公倍数の35づつ増えて行きます。つまり「はじめの数17,公差35の等差数列」になる。
不一致型の問題例
5で割ると2余り、7で割ると3余る数について答えよ
(1)小さい方から数えて5番目はいくつか→始めの数17、差35の等差数列の5番目だから、17+35×(5-1)=157
(2)500に一番近い整数はいくつか→N番目が500だとしてNを求めると、N=(500-17)÷35+1=14.8 なので、500の前後は14番目と15番目。14.「8」という数から15のほうが近いと予想がつく(一応確認すると、14番目=17+35×(14-1)=472、15番目=472+35=507 で15番目の方が近い)
(3)
個数を求める問題
約数と余り
約数を使うと「～を割ると～余る数」を簡単に表現できます。
＝(A-B)の約数でBよりも大きいもの
→→(120-8)=112の約数で8より大きいもの
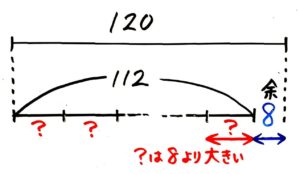
余りよりも大きいという制限に気をつけましょう。
例えば「120を割ると8余る数」は120-8=112の約数で8より大きいものです。
112の約数は1,2,4,7,8,14,16,28,56,112で、このうち8より大きいもの14,16,28,56,112が答えになります。
詳しい説明を読みたい人は「約数と余り(～で割ると余る数)」を見て下さい。
公約数と余り
「約数と余り」と同様に考えます。
公倍数と違って、余りが一致する必要はありません。
余りが一致しない場合
「Aを割るとB余り、Cを割るとD余る数」
＝(A-B)の約数でBより大きく、しかも(C-D)の約数でDより大きい数
＝(A-B)と(C-D)の公約数でBとDより大きいもの
例えば「130を割ると4余り、98を割ると8余る数」は「130-4=126と98-8=90の公約数で4と8より大きいもの」です。
126と90の最大公約数は18なので、126と90の公約数は18の約数 1,2,3,6,9,18です。
このうち4と8つまり8より大きいのは 9,18の2つです。
余りが一致する場合
余りが一致する場合は少し手軽です。
「Aを割ってもBを割ってもC余る数」
＝(A-C)と(B-C)の公約数のうちCより大きいもの
=(A-C)と(B-C)の最大公約数の約数のうちCより大きいもの
例えば
爽茶(公)倍数/約数の文章題
約数の文章問題
決まった大きさを「等しく分ける」分配する」区切る」のは約数の問題になる
多人数に平等に分配する
Z-1-1:平等に分配する
解説
45を子供の数で等分するので、子供の数は45の約数で1,3,5,9,15,45人が考えられる
ただ、子供「たち」なので1人よりは大きいと考えると、さきほどの45の約数から1を除いた3,5,9,15,45人の5通りが答えになる
解説
45個を一人あたりに配った数で等分するので、45の約数で1,3,5,9,15,45枚が考えられるが、45枚だと子供が1人になってしまうので、45を除いた1,3,5,9,15枚の5通り
(これは子供の数の5通りそれぞれに対応した枚数で、(1)と(2)の答えは同じになる)
公式化するとこんな感じ
「人数」→「1人あたりの個数」の順に決定
◆「人数」は合計個数の約数で1よりも大きい数
(例)45個の物を2人以上に平等に分配
人数は45の約数で1より大きい
→3,5,9,15,45人
◆「一人あたりの個数」は合計個数を人数で割った数
(例)3人の場合→45÷3=15個ずつ
5人の場合→45÷5=9個ずつ
9人の場合→45÷9=5個ずつ
15人の場合→45÷15=3個ずつ
45人の場合→45÷45=1個ずつ
多人数に平等に分配すると余る
Z-1-2:平等に分配すると余る
ヒント
実際に配った数を考えましょう
解説
4個余ったので実際に配ったのは100-4=96個。これを子供の人数で分ける(割る)ので、子供の数は96の約数。
しかも4個余っているので、子供の数は4よりも大きくないとオカシイ(4個余って子供が4人なら、もう1個ずつ配れる)。
つまり子供の数は96の約数で4より大きい数
96の約数は、1,2,3,4,6,8,12,16,24,32,48,96
この中で4より大きくて一番小さいのは6なので、考えられる子供の数として一番少ないのは6人
解説
(1)で出した子供の人数(96の約数で4より大きい数=6,8,12,16,24,32,48,96)が8通りで、1人に配る個数もそれぞれに対応して8通りある。
一番多く配るのは、一番少ない人数6人に配った場合だから、(100-4)÷6=96÷6=16個
実際に配った96個を、1人に配った数で分ける(割る)ので、1人に配った数は96の約数。これも4より大きくないとオカシイ(1人に4個ずつで4個余ったら、もう1個ずつ配れる)つまり、1人に配る数も子供の数もどちらも96の約数で4より大きい数なので、こちらも同じ6個が答えになる。
「人数」→「1人あたりの個数」の順に決定
◆「人数」は(合計個数-余り)の約数で、余りよりも大きい数
(例)39個の物を平等に分配したら7個余った
人数は39-32=32の約数で7より大きい
→8人,16人,32人
◆「個数」は人数に対応した数=(合計個数-余り)÷人数)
(例)8人の場合→32÷8=4個ずつ
16人の場合→32÷16=2個ずつ
32人の場合→32÷32=1個ずつ
(旧版たぶん間違い)
→「人数」も「一人あたりの個数」も
(合計個数-余り)の約数で、余りよりも大きい数
(例)39個の物を平等に分配したら7個余った
人数は39-32=32の約数で7より大きい
→8,16,32人
一人あたりの個数も32の約数で7より大きい
(人数が2人以上なら32よりも小さい)
→8,16個/人
倍数の文章問題
決まった大きさのものを「配る「重ねる「つなげる」と倍数の問題になる
Z-2-1:平等に配布する
ヒント
どうしてそんな大量のチョコがあるのかも気になりますが、とりあえず生徒の人数を出しましょう…
解説
5年生は30+28+29+31=118人なので、チョコの合計個数は118の倍数になる。
118の倍数で400以上500以下なのは118×4=472だけなので、チョコの合計個数は472個と分かる
公倍数の文章問題
異なる大きさのものを全く同じ個数ずつ「配る」ならべる」つなげる」のは公倍数の問題になる。
「公倍数は最小公倍数の倍数」を利用する
長方形をしきつめて正方形を作る(学校小5)
Z-3-1:長方形をしきつめる
ヒント
「正方形の一辺=縦の長さ=横の長さ」ですね
解説
しきつめて出来る図形の縦の長さは6の倍数、横は4の倍数で、縦と横が等しくなる一辺は4と6の公倍数つまり12の倍数になる。
したがって一番小さい正方形は一辺12cmである。
解説
縦の方向には一辺12cm÷長方形の縦6cmで2枚、横方向には12÷4=3枚並んでいるので、合計で2×3=6枚使っていると分かる
→大きな正方形の一辺は、
長方形の縦と横の公倍数になる。
(例)たて6cmよこ4cmの長方形をしきつめて
大きな正方形を作る場合
→大きな正方形の一辺は6と4の公倍数に
つまり12の倍数になる
直方体を集めて大きな立方体を作る
上と同じ考え方だが、こちらは大きな立方体の一辺が縦・横・高さの3つの数の最小公倍数の倍数になる
数パターンで余りなく配れる
Z-3-2:いくつかのパタ-ンで余りなく配れる
解説
アメの合計は8と12の公倍数、つまり24の倍数
200を超える一番小さい24の倍数は24×9=216なので、アメはすくなくとも216個あると分かる。
解説
アメの合計は8,12,20の公倍数つまり120の倍数
120の倍数で200以上300以下なのは120×2=240だけなので、アメの数は240個だと分かる
→合計個数は配る個数の公倍数になる
2種類のイベントが同時に起きる(学校小5)
間隔がそれぞれ異なるイベントが同時に発生するのは、「それぞれ間隔の最小公倍数」おきになる。
Z-3-3:複数のイベントが同時に起きる
解説
8と20の最小公倍数は40なので、各停と準急は40分おきに同時に出発する。
5:30+0:40=6:10より、次の同時出発は6時10分
解説
始発5：30から正午12：00までの6時間30分=390分を、同時出発の間隔40分で割ると、390÷40=9…30より、間隔が9個存在するのが分かる
植木算の考え方で、間隔(=間)が9個の場合イベント(=木)は1個多い10個なので、同時出発は10回になる。
周期で数える問題(受験小4)
間隔が異なるイベントの中身も問題になる場合は、最小公倍数の「周期」を見つけて、周期算にする。
Z-3-4:周期で計算する問題
ヒント
まず周期を出しましょう
解説
スイッチを入れてからAとBがはじめて製品を同時に完成させるのは3と5の最小公倍数の15分後
この15分間にAは15÷3×1=5個、Bは15÷5×2=6個の合わせて11個の製品を作る。次の15分でも同じようにABは11個の製品を作る。
この「15分11個」を一つの単位(周期)として考えると、100個の製品を作るのに、100個÷11個=9…1より、9周期と1個分の時間がかかると分かる。
9周期は15×9=135分、残り1個分はAが製品を1個作るのにかかる3分で、100個作るのには合計135+3=138分かかる
138÷60=2…18より、答えは2時間18分
ヒント
ロボットに昼休みはありません…
解説
9:30から16:40までは16:40-9:30=7:10=430分。
この間に「15分11個」の周期がどれくらい存在するか計算すると430分÷15分=28…10より28周期と余り10分と分かる。
28周期では11個x28周期=308個の製品が作られ、さらに10分でAが10÷3×1=3個、Bが10÷5×2=4個の計7個を作る
合計で308+7=315個の製品ができる。
公約数の文章問題
異なる大きさの物を全く同じ大きさに分ける場合は公約数の問題になる
大きな長方形を正方形に切り分ける(学校小5)
Z-4-1:正方形に切り分ける
ヒント
方眼に沿って切るので1cm単位で切ります
解説
等しく切り分けるので、切り分けた縦の長さは60の約数、横の長さは42の約数、正方形の一辺は60と42の公約数になる。
一番大きな正方形の一辺は60と42の最大公約数なので、6cmになる
解説
一辺6cmなので、縦方向に正方形は60÷6=10個、横方向には42÷6=7個並んでいる。
したがって正方形の個数は10×7=70個と分かる。
→正方形の一辺は長方形の縦横の公約数になる
(例)
大きな直方体を小さな立方体に切り分ける
上と同様だが、こちらは小さな立方体の一辺は直方体の縦・横・高さの3つの数値の公約数になる
多品目を平等に分配する(受験小4)
Z-4-3:多品目を平等に分配
解説
60と42を同じ数(子供の数)で等分する(割る)ので、子供の人数は60と42の公約数で1より大きい数(子供「達」なので)つまり最大公約数6の約数(1,2,3,6)のうち1より大きい2人,3人,6人になる。
それぞれの場合で配る個数は、アメは60÷人数、ガムは42÷人数になる。
1人に配る個数が少なくなるのは人数が多いときなので6人の場合で、このときのアメとガムの個数を出せばよい。
アメは60÷6=10で最小10個、ガムは42÷6=7で最小7枚と分かる
このように「多品目を平等に分配する場合」を公式にすると
「人数」→「1人あたりの個数」の順に決定
◆「人数」は合計個数の公約数で1よりも大きい数
(例)60個のアメと42個のガムを平等に分配
人数は60と42の公約数で1より大きい数
→2,3,6人
◆「一人あたりの個数」はそれぞれの合計個数を人数で割った数
(例)2人→アメ60÷2=30個ずつ,ガム42÷2=21個ずつ
3人→アメ60÷3=20個ずつ,ガム42÷3=14個ずつ
6人→アメ60÷6=10個ずつ,ガム42÷6=7個ずつ
こうなりますね
多品目を平等に分配すると余る(受験小4)
Z-4-4:多品目を分配すると余る
ヒント
まず配った人数を決定
解説
実際に配った数はアメ108個、ガム72枚。これを同じ数(子供の人数)で等分する(割る)ので、子供の人数は108と72の公約数で、6より大きい数=36の約数で6より大きい数で、9人,12人,18人,36人の4通り
一番多く配るのは、子供の数が一番少ない9人の場合で、このときアメは108÷9=12個ずつ、ガムは72÷9=8枚ずつになる
このように多品目を分配すると余る場合を公式にすると
「人数」→「1人あたりの個数」の順に決定
◆「人数」は「品目の合計-余り」の公約数で、
どの余りよりも大きい数
(例)アメ114個とガム76枚を子供たちに平等に配ったところ、
アメは6個、ガムは4枚余った
→人数は114-6=108と76-4=72の公約数で
6より大きい数→9人,12人,18人,36人
◆「1人あたりの個数」は(品目の合計-余り)÷人数で求める
(例)9人→アメ108÷9=12個ずつ,ガム72÷9=8枚ずつ
12人→アメ108÷12=9個ずつ,ガム72÷12=6枚ずつ
18人→アメ108÷18=6個ずつ,ガム72÷18=4枚ずつ
36人→アメ108÷36=3個ずつ,ガム72÷36=2枚ずつ
となります
多品目を平等に配ると余る品目がある
Z4-4-5:1品目が余る
ヒント
ここでも、実際に配った人数を出しましょう
解説
実際に配った数は48枚と177-9=168個なので、人数は48と168の公約数で9よりも大きい数
48と168の最大公約数は24なので、
(慣れてきたら素因数より
大きい数で割っても良い)
48と168の公約数は24の約数で1,2,3,4,6,8,12,24
このうち、9より大きいのは12と24なので、参加者の人数として考えられるのは12人と24人
分かりましたか？
公倍数公約数の文章題は以上です
プリントダウンロード
このサイトで使用した(公)約数倍数プリント をまとめてダウンロードできます♪
zipファイルの中に問題だけのPDFと解答だけのPDFが入っているのでご利用下さい。
著作権は放棄しておりません。無断転載引用はご遠慮下さい。
ダウンロードにはパスワードが必要です。こちらから会員登録すると自動返信メールですぐパスワードを受け取れます。
Error! Please enter an ID value with this shortcode.
会員登録すると「そうちゃ式」全サイトで使えるパスワードをメールですぐにお知らせします。
オススメ教材
爽茶分かりやすい！と評判のスタディサプリにも約数・倍数の授業動画がありますよ。今なら14日間無料。興味がある人は「先取りや予習・復習に！ スタディサプリ そうちゃ式のオススメ利用法」へ
●約数倍数だけを解きたい場合は「思考力算数練習帳シリーズ」の「倍数・公倍数」
●算数全体の復習をしたい場合、小4受験生には「算数の基本問題(小5)」(日能研)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!
保管セクション
60をすだれ算で素因数分解していく例
30÷2=15→ 2)30
15÷3=5→ 3)15
5
60＝2×2×3×5
左に(縦に)並んだ数をかけると最大公約数になり、
左と下に(横に)並んだ数全部をかけると最小公倍数になる。
二つの数しか割れない場合、最大公約数に注意