「100に近い~と~の公倍数」のような問題の解き方を復習したい中学受験生の方、お任せ下さい。
東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
決められた範囲と倍数
解き方を理解
例題2(範囲内での倍数)
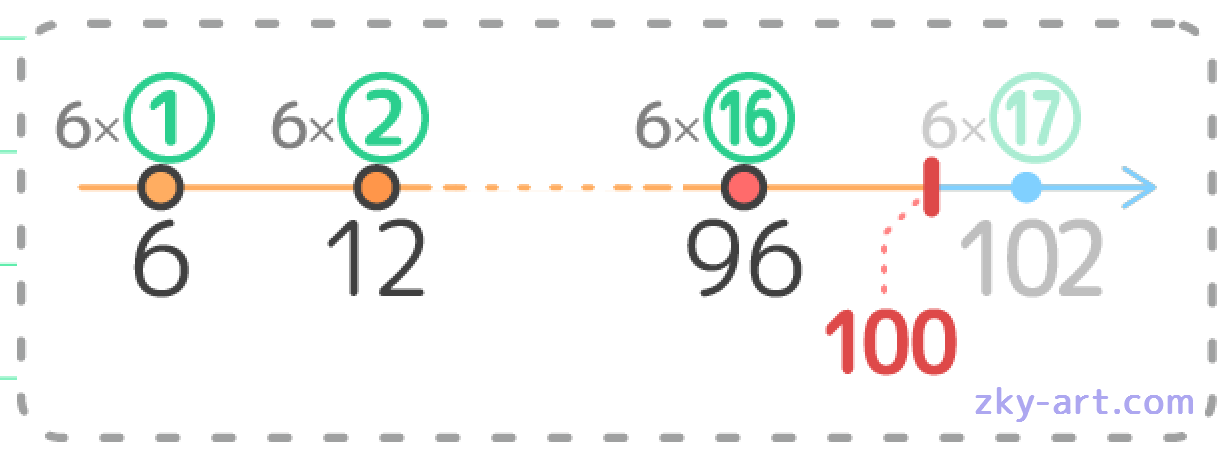
6の倍数について、以下の問いに答えなさい。
- 6の倍数で一番大きいのは何か?
- 100より小さい6の倍数の中で一番大きいものは?
- 6の倍数の中で100に一番近いのは何か
例題2-(1)
悩まず気楽に答えてください
高校生なら「∞」と答えても良いかもしれませんが
(^_^;)
小学生の範囲で考えます。
6の倍数は6×1から始まって、6×10…6×1000…6×1000000…と永遠に続いてしまいます…ですから、答えは、ありませんですね
答: 答えられない
ちょっと意地悪な問題でした
では、気を取り直して…
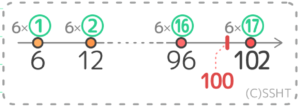
例題2-(2)
例題2-(3)
このように、範囲が示される場合でも「より小さい」なのか「に近い」なのか、条件をよく読むことが大切です。
では、類題で練習して下さい。
類題で定着
類題2-1
100÷7=14.…(割り切れない)ので、7×14と7×15を調べます。
7×14=98 と 7×15=105 で差を調べると…100-98=2 と 105-100=5 なので、98の方が100に近いと分かますね。
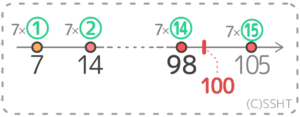
答: 98
類題2-2
最初の例題で書いた通り、「17で割り切れる数」=17の倍数です。
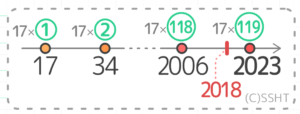
2018÷17=118.…(割り切れない)ので、17×118と17×119を調べます。
17×118=2006 と 17×119=2023 で2018との差を調べると、2018-2006=12 2023-2018=5 で2023の方が2018に近いと分かります。
答: 2023
類題2-3
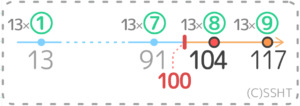
100÷13=7.…(割り切れない)13×7=91 で、その次は13×8(または91+13)=104です。
この後はどんどん大きくなるだけなので、この104が「100より大きい13の倍数の中で一番小さい数」と分かります。
答: 104
プリントダウンロート
画像をクリックするとプリントが表示されますので保存して下さい。
メアド等の入力は必要ありませんが、著作権は放棄しておりません。無断転載引用はご遠慮ください。
範囲と公倍数
解き方を理解
決められた範囲(内)での公倍数の最大を求める問題です。ただの倍数の問題に直すのがコツです。
倍数の問題の解き方は「倍数の意味・範囲」内の倍数と範囲の問題を見て下さい。
例題3(範囲内での倍数)
2と3の公倍数に関する以下の問いに答えなさい。
- 100より小さい6の倍数の中で一番大きいものは?
- 6の倍数の中で100に一番近いのは何か
2と3の最小公倍数が6なので「2と3の公倍数」は「6の倍数」になります。
ですからこの問題は「2と3の公倍数」を「6の倍数」に変えて、こうなります。
例題3′(範囲内での倍数)
6の倍数について、以下の問いに答えなさい。
- 100より小さい6の倍数の中で一番大きいものは?
- 6の倍数の中で100に一番近いのは何か
では、倍数の復習のつもりで解いていきましょう
例題3′-(1)
次の小問は条件が変わるのに注意しましょう。
例題3′-(2)
では類題を同じ様に解いてみてください。
練習問題で定着!
類題3
3でも4でも割り切れる数に関する以下の問いに答えよ
(1)100に一番近い数は何か?
(2)200に一番近い数は何か?
「3でも4でも割り切れる数」は「3と4の公倍数」と同じです。そして「3と4の公倍数」は「『3と4の最小公倍数』の倍数」です(早口言葉みたいでこんがらがりますね…)
そこで、まず「3と4の最小公倍数」を求めましょう。
4の倍数を書いていき、3の倍数でもある数が出てきたら、それが最小公倍数です。
4,8,12 出てきました。3と4の最小公倍数が12と分かりました。
これで、この問題はどうなりますか?
(1)100に一番近い数は何か?
(2)200に一番近い数は何か?
と同じになります。
類題3′
12の倍数に関する以下の問いに答えよ
(1)100に一番近い数は何か?
(2)200に一番近い数は何か?
「一番近い」なので100や200を超えても良いことに注意しましょう。
●類題3′-(1)
100÷12=8.…なので、12×8=96と次の数96+12=108のどちらが100に近いか調べると、
100-96=4,108-100=8なので、96の方が100に近いと分かります。
答: 96
●類題3′-(2)
200÷12=16 なので、12×16=192、192+12=204
200-192=8 ,204-200=4 なので、204の方が200に近いと分かります。
答: 204
プリントダウンロード
画像をクリックするとプリントが表示されますので保存して下さい。メアド等の入力は必要ありませんが、著作権は放棄しておりません。無断転載引用はご遠慮ください。


次のステップへ
 爽茶
爽茶→公倍数公約数のまとめに戻る
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ