倍数の基本は分かったので、問題に挑戦したい中学受験生の方、お任せ下さい！東大卒講師歴20年の図解講師「そうちゃ」が倍数の個数の求め方をまとめました♪特に「ケタ数指定の問題」は入試でもよく出題されますよ。
倍数の個数問題
(単純指定)
こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
今回の「倍数の個数」は問題の形式や解法が決まっているので比較的点数を取りやすい問題ですから、算数が苦手な人も必ずマスターしましょう！
まず、倍数の個数を求め方を説明します。「気楽に」はじめましょう
例題1
(1)7の倍数はいくつあるか？
(2)１から１００の間に７の倍数はいくつあるか
小問1
(ヒント)
気楽に考えましょう
[su_spoiler title=”気楽に答えを見る” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
前回見たとおり、
７の倍数は無限に大きくなっていくので、無数にあるということです。いくつあるかは、数えられません
答: 数えられない
ただの意地悪問題ではないんです
(^_^;)
制限をつけない限り倍数は無数にあると覚えておきましょう！
[/su_spoiler]
小問2
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
今度は制限があるので答えが決まります。
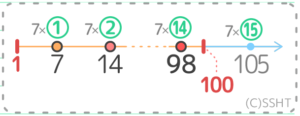
前回の例題を思い出すと、100÷7＝14.… から、こういう図が出来ました。(初めの「1」を付け加えています)
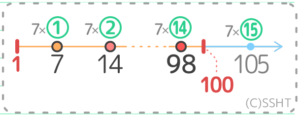
この図から、1から100までの間に7の倍数は14個あると分かります。
つまり、100÷7の整数部分(余りを無視した答え)がそのまま７の倍数の個数だったのですね。
答: 14個[/su_spoiler]
このように「1からの」範囲が指定された場合の処理は公式として覚えましょう。
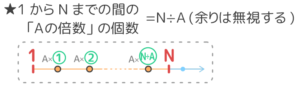
はじまりは必ず「1から」です。
正直なところ、このような単純指定の問題は受験ではあまり出ませんが
(^_^;)
この次の問題の基礎になるので速く正確に解けるように類題で練習！です
類題1
公式にあてはめるだけですね
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
N=100,A=13なので、100÷13=7…9 より 余りを無視して7個と分かりますね。
答: 7個[/su_spoiler]
類題2
これも公式の練習ですね
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
N=2018,A=17 なので、2018÷17=118…12 より 余りを無視して118個と分かりますね。
答: 118個[/su_spoiler]
倍数の個数問題
(ケタ数指定)
ここからが本番です！
いつものように、始めは誘導形式で行きます。
例題2
(1)「1ケタの数」とは、いくつからいくつまでか？また「２ケタの数」とは、いくつからいくつまでか？
(2)1から99までの間に、7の倍数は何個あるか。また、その中に2ケタでないものは何個あるか
(3)結局、7の倍数のうち2ケタのものは何個あるか？
(4)7の倍数のうち、3ケタのものが何個あるか求めなさい
小問1
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
まず、1ケタの数とは1から9までです
そして、2ケタの数とは10から99までですね
答: 1から9まで,10から99まで
ちなみに、3ケタの数は100から999までですね。
[/su_spoiler]
さて、このように2ケタの数の範囲が分かりました。
しかし、先程の公式は「1から」の範囲でしか個数が求められないので「10から99まで」は求められません！！
(>_<)
一体どうすれば良いでしょうか…
小問2
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
先程の公式
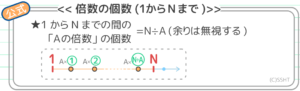
を使って、99÷7＝14…1 で 1から99までの間に7の倍数は合計14個あります。
その14個の7の倍数のうち、一番初めの「7」だけが1ケタなので
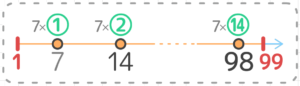
2ケタでないものは1個と分かります。
答: 14個,1個[/su_spoiler]
小問3
もうお分かりですね？
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
小問1で求めた7の倍数14個のうち、はじめの「7」1個以外は2ケタなので、14-1＝13個と分かりますね
答: 13個[/su_spoiler]
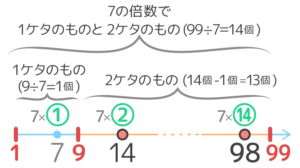
このように、2ケタの倍数を出す場合は1ケタと2ケタの倍数の合計個数から1ケタの倍数の個数を引いて求めます。
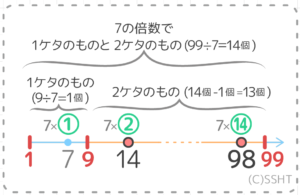
1ケタの数は「1から9」の間にあるので、1ケタの倍数の個数は9÷Aで求められます。
この考え方を使えば、3ケタの場合も分かりますね？
小問4
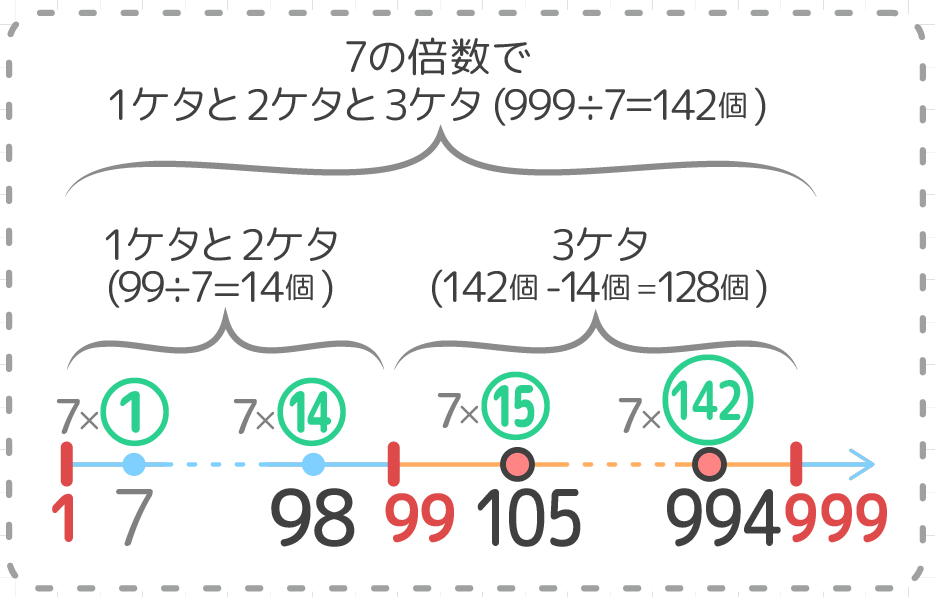
まず、7の倍数で1ケタ2ケタ3ケタの合計個数を出すと
[su_spoiler title=”いくつですか？” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
999÷7＝142個 ですね[/su_spoiler]
次に、7の倍数で1ケタ2ケタの合計個数を出すと
[su_spoiler title=”いくつですか？” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
99÷7＝14個 ですね[/su_spoiler]
したがって、3ケタのものは、
[su_spoiler title=”いくつありますか？” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
142-14＝128個と分かります
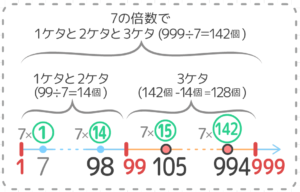
答: 128個[/su_spoiler]
以上の処理を公式にすると、こうなります！
試験場で瞬時に計算に入れるよう覚えておきましょう。
上にある図も書けるようにしておくと、応用問題にも対応できるようになりますよ！
では、類題で練習しましょう♪
類題2-1
公式にあてはめてサクッと出して下さい
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
２ケタを求めるので
公式のうち2番目のものを使います。
A=3 を公式にあてはめて
(99÷3)-(9÷3)＝33-3＝30個になります
答: 30個[/su_spoiler]
類題2-2
簡単ですね？
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
「13で割り切れる数」＝「13の倍数」でしたね
3ケタを聞かれているので
公式の3番目の式に
A=13をあてはめて
(999÷13)-(99÷13)＝76-7＝69個ですね
答: 69個
計算ミスに気をつけましょう
(・ω・;)[/su_spoiler]
類題2-3
桁数ではありませんが、同じ考え方で解けますね
(*^ーﾟ)ｂ
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]
1から1000の間の13の倍数の個数から、1から259の間の倍数の個数を引けば良いですね。(1から「260」では無い事に注意！！)
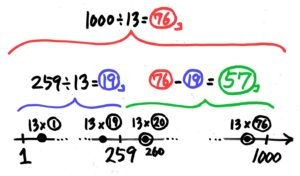
手書きだと、こんな感じですね
(1000÷13)-(259÷13)＝76-19＝57個と分かります
答: 57個[/su_spoiler]
以上で、倍数の個数を求める問題は終了です
お疲れ様でした！
次のステップへ
まとめ
Aの倍数の個数(例:7の倍数)
❶1からNまでの範囲内→N÷A(余り無視)個
(例:１から100までに７の倍数は100÷７=14個)
❷ケタを指定される場合
●２ケタのもの→「(99÷A)-(9÷A)」個
(例:７の倍数で２ケタ→(99÷7)-(9÷7)=13個)
●３ケタのもの→「(999÷A)-(99÷A)」個
(例:７の倍数で２ケタ→(999÷7)-(99÷7)=128個)
爽茶→(公)約数/倍数のまとめに戻る
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!