「N進法」と聞いて「何それ…難しそう!」「苦手!塾の授業がよく分からなかった…」と思ってしまう中学受験生の方へ
大丈夫ですよ!だって皆さんは普段から「10進法」を使っているんですからね。
一度きちんと「10進法」の仕組みを知れば「2進法」でも「3進法」でも必ず理解できますよ♪
この記事では東大卒講師歴20年の図解講師「そうちゃ」が、10進法の仕組みから初めてN進法の応用問題まで分かりやすく説明します。
記事を読んで例題を解けば、N進法が好き/得意になるでしょう♪
数の仕組み(10進法)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
はじめに、私達が普段使っている数の仕組みを深堀りします♪
数の作り(復習)
ケタの名前
ケタの読み方
右端(一の位)から4ケタづつ区切って、4ケタまとめて左から読む
「123456789012」→「1234,5678,9012」
→「1234億5678万9012」
→「せんにひゃくさんじゅうよん億,ごせんろっぴゃくななじゅうはち万,きゅうせんじゅうに」
数の大きさ=10進法
「234」を何と読みますか?
普通は「にさんよん」とは読まずに「にひゃくさんじゅうよん」と読みますね。
これは「234」を右から「一の位」「十の位」「百の位」と考えて、1×4+10×3+100×2=(100×2)+(10×3)+(1×4) と直しているからですね
普段何気なく使っている、この仕組みを「10進法」といいます。
●意味
➀ある位の数が10コ集まると次の位に繰り上がる仕組み
②「0」から「9」までの10種類の数字で大きさを表す
●位の大きさ(右から)
1の位,10の位,100の位,1000の位…
1000の位
100の位
10の位
1の位
●数の大きさ(例「2312」)
(1×2)+(10×1)+(100×3)+(1000×2)
=2312
確認テスト
「50293」が表す数の大きさを十進法の表現に直しなさい
→(10000×5)+(1000×0)+(100×2)+(10×9)+(1×3)
N進法の仕組み
N進法の意味
10進法では、ある位の数が10個集まると上(左)の位に繰り上がりました。
例えば「149」に1を加えると…、一の位に数が10個たまって繰り上がりが発生して「150」になりますね

繰り上がりが発生する
これを2個集まると繰り上がるようにすると、例えば「101」に「1」を加えるだけで、繰り上がりが発生します。
(=2進法!)
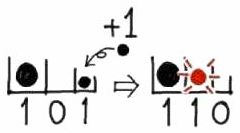
繰り上がりが発生する(早!)
この仕組みは、2個で繰り上がるので「2進法」と言います。

繰り上がりが発生する
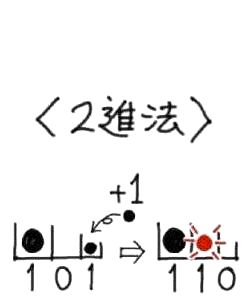
繰り上がりが発生する
N進法の位取り
普段使っている10進法では、位は右端から「一」「十」「百」にとなっています。なぜ「一」「二」「三」ではなく「一」「十」「百」になるのでしょう?
10進法では数10個で繰り上がるので、右端を「1」の位とするとその左となりの位は「1」が10個分なので「10」の位、その左となりの位は「10」が10個分なので10×10=「100」の位、次は100×10=「1000」の位…というふうに位を決めているんですね
つまり、10進法の位は右から「1」「10」「10×10」「10x10x10」…となります
10×10×10
1000の位
10×10
100の位
10
10の位
1
1の位
この考え方で、10以外の数のしくみも作れますね!
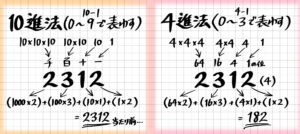
例えば、上の図と同じ「2312」でも4進法だとどうなるでしょうか
「4」進法なので右から「1」「4」「4×4」「4x4x4」、つまり「1の位」「4の位」「16の位」「64の位」となります(最初は10進法と同じく「1」なのに注意)
4×4×4
64の位
4×4
16の位
4
4の位
1
1の位
このように、N進法の位は「1の位」「Nの位」「NxNの位」「NxNxNの位」…と決まっていきます
→Nのかけ合わせて決まっていく
「1の位」「Nの位」「NxNの位」「NxNxNの位」…
(例)4進法の場合…
「1の位」「4の位」「16(4×4)の位」「64(4x4x4)の位」
4×4×4
64の位
4×4
16の位
4
4の位
1
1の位
確認テストをどうぞ
2進法の位取りは右端からどうなっているか?
→(2をかけ合わせるので、右端から「1の位」「2の位」「4(2×2)の位」「8(2x2x2)の位」「16(2x2x2x2)の位」となる)
(参考)日常生活のN進法~時間
日常生活で使っているN進法もあります。それは時間です。
1秒・2秒…と増えていって1分になるのは、60秒後です。これは60で繰り上がりが発生しているので60進法と言えますね。
次に1分・2分…と増えていき1時間になるのは60分後で、これも60で繰り上がっているので60進法です。
そして1時間・2時間…と増えていき1日経つのは…60時間後でなく24時間後なので、ここでは繰り上がりが24で発生する24進法になっています。
ここまではきっちり1種類に決まった繰り上がりですが、この上の単位「月」「年」は不規則な繰り上がりになります。
「日から年」は30日・31日・28日・29日(うるう年)と4種類の繰り上がりがあり、「日から年」も365日か366日(うるう年)の2種類の繰り上がりがありますね。
ただ、「月から年」は12ヶ月で1年と決まっているので12進法の一種類です。
●秒→分:60進法(60秒で1分)
●分→時:60進法(60分で1時間)
●時→日:24進法(24時間で1日)
●日→月:だいたい30進法
(30日/31日/28日/29日)
●日→年:だいたい365進法
(365日/366日)
●月→年:12進法(12ヶ月で1年)
N進法が表す数の大きさ(N進法→10進法)
N進法の位取りの仕組みが分かれば、もう問題が解けます♪
例えば、問題集のN進法の単元の最初の問題「4進法の2312が表す大きさはいくつか」という問題。
これは「4進法を10進法に直すといくつになるか」と同じことを聞いています。
1:N進法を10進法に直す
ヒント
普通の(10進法の)2312が表す大きさを式にして、それを4進法に応用する♪
解説
10進法では位が「1の位」「10の位」「100の位」「1000の位」だったので、
10進法「2312」が表す数の大きさは、(1000×2)+(100×3)+(10×1)+(1×2)=2312と計算しました。
つまり
数の大きさは「位の大きさx位の数」の合計で決まっています。
4進法でも同じように計算します♪
4進法の位は右から「1の位」「4の位」「16(4×4)の位」「64(4x4x4)の位」となっていましたね
よって、4進法の「2312」が表す数の大きさは(64×2)+(16×3)+(4×1)+(1×2)=182と計算できます。
4×4×4
64の位
4×4
16の位
4
4の位
1
1の位
=182が数の大きさになる
例題2(16進法)
N進法のNが10より大きい場合もあります。例えばコンピュータの世界で使われる16進法です。
16進法は「0」から「9」に加えて「A(=10)」「B(=11)」「C(=12)」「D(=13)」「E(=14)」「F(=15)」の合計16個の字を使います。
位取りは大きな数になります…右から「1の位」「16の位」「256(16×16)の位」「4096(16x16x16)の位」…になります。
(1)16進法の「A3F」が表す数の大きさはいくつか?
もっと問題を解きたい人は、記事下の「オススメ教材」を見て下さい
小まとめ
●意味
➀ある位の数が10コ集まると次の位に繰り上がる仕組み
②「0」から「9」までの10種類の数字で大きさを表す
●位の大きさ(右から)
1の位,10の位,10×10の位,10×10×10の位…
10×10×10
1000の位
10×10
100の位
10
10の位
1
1の位
●数の大きさ(例「2312」)
(1×2)+(10×1)+(100×3)+(1000×2)
=2312
確認テスト
●意味
➀ある位の数がN集まると次の位に繰り上がる仕組み
②「0」から「N-1」までのN種類の数字で大きさを表す
(例)4進法
各位の数が4コ集まると繰り上がる仕組み
「0」から「3」までの4種類の数字で大きさを表す
●位の大きさ(右から)
1の位,Nの位,N×Nの位,N×N×Nの位…
(例)4進法
左から1の位,4の位,16(4×4)の位,64(4x4x4)の位
4×4×4
64の位
4×4
16の位
4
4の位
1
1の位
●数の大きさ(例「2312(4)」)
(1×2)+(4×1)+(16×3)+(64×2)
=182
10進法→N進法
今度は10進法をN進法に直します。例えば10を2進法になおしてみましょう。
2進法の位は右から「1の位,2の位,4の位,8の位,16の位」だったので、右から4つめの8の位に「1」が立つのは分かります(「1???」)
そして10-8=2が残りの数なので、一つ右隣の4の位は「0」で(「10??」)、そのとなりの2の位に「1」が立って(「101?」)、終了です(「1010」)。
これで、10進法の「10」は2進法では「1010」になると分かりました。ちなみに「1010」だと10進法の「せんじゅう」と区別がつかないので、「1010(2)」と右下に2進法の印をつけます。
公式化
いちいち上のように考えるのも面倒くさいので、もっと気軽に2進法に直す方法を教えます。
最初の2進法の仕組みの図を思い出して、一番右の「一の位」に数(玉)をどんどん入れていくのを想像して下さい。

繰り上がる(クリアされ隣に1個入る)
2進法は「ケタに数が2個集まると繰り上がりが発生する」数でしたから、全部入れ終わって一の位に残っている玉の数は、2個入れれば2個繰り上がって残り0、3個入れれば2個繰り上がって残り1個、4個入れれば2回2個繰り上がって0…というふうに2で割った余りになりますね。
この問題では数(玉)を10個入れるので、10÷2=5…0より、繰り上がりが5回発生して、1の位は0(玉が残っていない)と分かります。
そして繰り上がりが5回発生したので、次の2の位には数(玉)が5個入ります。この2の位では、5÷2=2…1より2回繰り上がりが発生して1残ると分かります。
この計算を2の割り算ができなくなるまで行ったのが、下図です。
最後の段は、2÷2=1…0で終わっています。この1から「L」の字を描くように余りを読むと「1010」になって、これが答えです。
時間計算での説明
分→秒→時間は60進法なので、これを使った説明だと理解しやすい人もいるでしょう。
例えば、9030秒(10進法)が何時間何分何秒(60進法)に直すのを考えます(今まで習った方法とは違うかもしれません)。
9010秒÷60=150余り10 から、9030秒は150分10秒と分かります。
次に150分÷60=2余り30 から、150分は2時間30分と分かります。
2つの計算を合わせて、9010秒は2時間30分10秒と分かります。
分かりましたか?
例題を解いてみましょう♪
3:10進法→N進法
ヒント
35を3で割って答えと余りを下に連ねていきましょう♪
解説
35÷3を行うと?
35÷3=11…2 を35の左と下に記入します
次の計算は…
11÷3=3…2 を11の左と下に記入します
次で最後です
3÷3=1…0 を記入します。
下からL字型に読むと「1022」で、これが3進法に直した答えです!
ヒント
同じようにGo♪
解説
68÷5=13…3 → 13÷5=2…3 で終了です。あっと言う間でした(汗)
下からL字型に読むと「233」ですね
ヒント
大きい数ですが確実にGo♪
解説
こうなりますね
下からL字型に読むと「1645」ですね
もっと問題を解きたい人は、記事下の「オススメ教材」を見て下さい。
[作成中]N進法の文章問題
考え方
難しく考えすぎないことが大切で、要するに何進法か見抜くようにしましょう
10進法は「0」から「9」までの10個の数字を使った仕組みであることを思い出し、一つの位や部品に何種類の記号や状態があるかを考えれば良い。
たとえば、マス目を使った下のような問題の場合
((図))
ひとかたまりのマス目には「」「」「」「」の4つの状態があると分かります。(「」という状態はありません)
4つの状態=4つの数字を使った数え方なので、これは4進法になります
そして、この仕組は問題の中では変わらないのが普通なので、後は小問ごとに「4進法→10進法」と「10進法→4進法」のどちらの問題かを判断して、上で練習したように解けば良いわけです。
では実際に解いてみましょう
マス目の問題
電球の問題
メーターの問題
その他の問題
[作成中]変則N進法の問題
ちょっと変則的な文章題で、これが解ければ難関中学でも受験者平均点は取れるでしょう
禁じられた数字(怖)
縁起を担いで、特定の数字を使わずに番号をつけていく問題
部屋番号に4と9を使わないホテル
4(死)と9(苦)を縁起が悪いとして使わずに部屋番号を決めたホテルがあるとします
部屋の番号は「1」「2」「3」(4なし)「5」「6」「7」「8」(9なし)「10」「11」「12」「13」(14なし)「15」…と増えていきます。
ゼッケン番号に397を使わないマラソン大会
限定された数字
5963だけの肩たたき大会
37564だけの武闘大会
オススメ教材
 爽茶
爽茶●N進法だけの問題集は見当たりませんが、その他の単元を合わせて予習復習をしたい場合、「算数の基本問題」シリーズ(日能研)
●小6受験生には「算数ベストチェック」(日能研)
「分かりやすい!」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては?
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
