「数列を予習したい」習い始めたけれど分かりづらい」と感じている中学受験生の方へ。東大卒講師歴20年の図解講師「そうちゃ」が数列を分かりやすく図解します。
この記事の最後でプリントがダウンロードできますので是非ご利用下さい。
等差数列とは？
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
説明よりも問題を解きたい人はコチラにジャンプして下さい。
等差数列のしくみ
さて問題です。この「数字の列」を見て下さい。
2 , 5 , 8 , 11 …
次の数字が何か分かりますか？(▼をクリック)
14です！正解したアナタは「この数字の列はメチャクチャな並びでは無く、ルールがある」分かったということですね。素晴らしい！
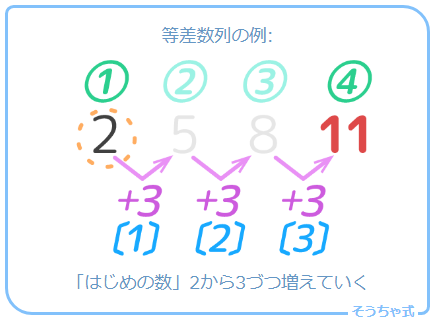
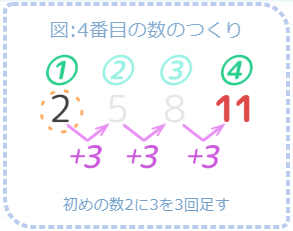
この数字の「ルール」というのは、一番左の「2」から右に一つ進むにつれて3ずつ増えていく、というものです。
このように等しい差で増えていく数字の列を等差数列と言います。
数字がたくさんあるので、呼びやすいように名前をつけます。
- 一番左の(最初の)数
=「はじめの数」(「1番目の数」) - 等しい増え分(差)
=「公差」(「公」は「共通の」という意味)
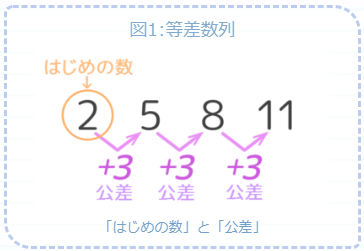
解く前に…○を書き込む
数列を見たら、まず数の差を書き込みましょう。差が等しければ等差数列です(図1)。さらに数字の上に番号を書き込みます(図2)
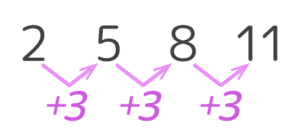
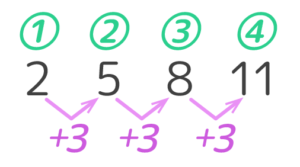
これで問題を解く準備が終了です。
爽茶等差数列の「N番目の数」を求める
爽茶今回は「N番目の数」を出す問題です。
まず誘導形式で解き方を理解して下さい！
考え方を理解♪
実は数列の問題は時間さえあれば初めから書いて求められます。
しかし、その方法だと「1000番目」には対応できません(汗)。
そこで、計算で求める方法(公式)を考えます
例題1
気楽に考えて下さい♪
●例題1-1(1)
初めの数2に公差3を加えているので「5＝2＋3 」と表せますね。
5＝2＋3
●例題1-1(2)
3番目の「８」は、初めの数2に公差3を2回足しているので「8＝2＋3+3 」と表わせます。
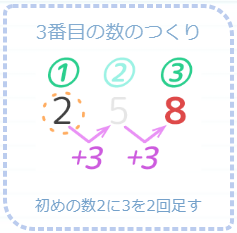8=2＋3+3
●例題1-1(3)
4番目の数「11」は、公差3を3回足しているので
「 11＝2＋3+3+3 」と表せます。
11=2＋3+3+3
+3を何度も書くのが面倒くさくなりましたね？(私もですｗ)
そこでこの部分を掛け算にすると、こうなります。
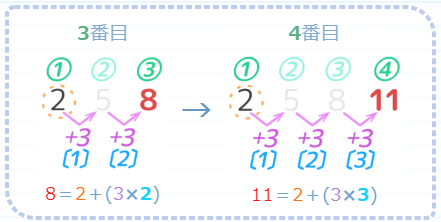
上の図を見て「あれ？」と思ったあなたは鋭い！
そうです。3番目の数を出すのに+3を3回ではなく2回、4番目の数を出すのに+3を4回ではなく3回足しているのですね。
つまり、等差数列に出てくる数は「自分の番目より1つ少ない回数分の公差を「初めの数」に足した数」になります。
例えば、100番目の数なら100-1で公差を99回足し、1000番目の数なら1000-1で999回足すことになります。
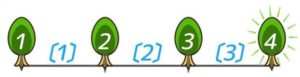
なぜ公差の回数が番目より1少なくなるかというと、植木算と同じです。
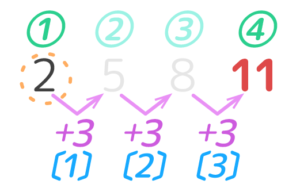
木が4つなら間の数は1少ない3つになりました。(図1)。数列の場合は数が4つなら公差は1少ない3つになります(図2)
興味がある人復習したい人は「植木算の基本：直線状に並べた植木」を読んで下さい。
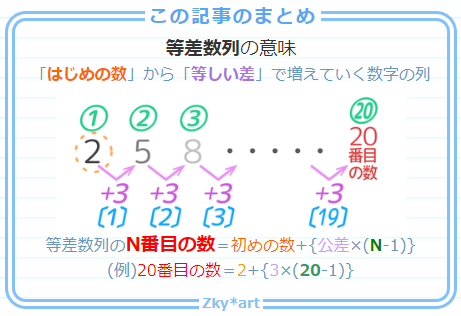
「N番目の数」の公式
今の考え方を、もう少し覚えやすい形の「公式」に直すと、等差数列のN番目の数は「初めの数+{公差×(N-1)}」と表すことができます。
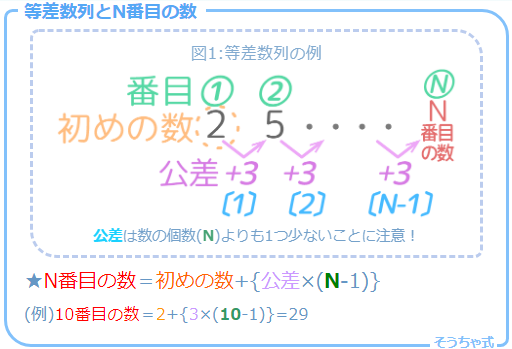
この公式を使えば、1000番目でも計算で出せますね!
試しに20番目の数を出しましょう。
●例題1-2
公式「N番目の数＝初めの数+{公差×(N-1)}」を使います。
公式を使うときは公式の形を崩さずに、数字を入れていきます。
これを「代入(だいにゅう)」と言います。(くわしく読むには▼をクリック)
「代入」はハンバーガーの中身だけをハンバーグからテリヤキチキンに変えるような作業です。
チキンバーガーに変わっても、全体の「形」は上から「パン→中身→パン」と変わっていません。
関連記事「算数が苦手な子には『公式』と『代入』を」を見て下さい。
この問題では公式の最初の「N番目の数」の「N」の代わりに20を入れて「20番目の数＝」にします。
続いて、「初めの数」に2、「公差」に3，「N」に20を入れて、答えを出すと…(▼をクリック)
20番目の数＝2+{3×(20-1)} という形になります。{3×(20-1)} の部分を先に計算することに注意して下さい。
これを計算すると2+{3×19}＝2+57＝59です。59
爽茶このように、等差数列の「N番目の数」は公式に入れれば簡単に出すことができます。
類題で公式の使い方を練習しましょう！
練習問題で定着！
類題1
「N番目の数＝初めの数+{公差×(N-1)}」
はじめの数は3、公差は7、Nは13 です。
公式に入れると、13番目の数＝3+{7×(13-1)} です
計算すると3+7×12＝3+84＝87です。87
次はルールが少し変わった問題です。
類題2
公式が変わります。
N番目の数＝初めの数－{公差×(N-1)}
減っていく数列では、もとの公式
「N番目の数＝初めの数+{公差×(N-1)}」
のプラス(+)をマイナス(ー)に変えて、こうなります。
N番目の数＝初めの数－{公差×(N-1)}
初めの数＝98、公差＝3、N＝15 をこの公式に入れると、15番目の数＝98－3×(15-1)となります。
これを計算すると98-3×14＝98-42＝56です。
56
次は文章題です(作成中)。
貯金(貯水)の問題
バネの問題
ろうそく(消費・排水)の問題
最後は、応用問題です。
●応用類題
この類題では植木算で学習した「番目」と「番差」を使います。「番目」は植木「番差」は間と同様に考えて、こうなります
「番差」＝「番目」－1
「番目」＝「番差」+1
忘れた方、未見の方は関連記事「番号付き植木算」を見て下さい。
類題1(1)
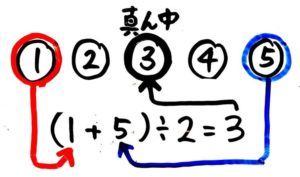
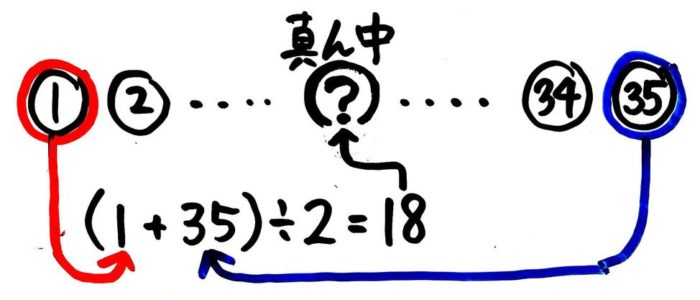
まず、真ん中が何番目か(N)を求めます。
奇数(1,3,5…)個の物が並んでいる場合、最初の番号と最後の番号の合計を2で割った答えが真ん中の番号になります。
奇数(1,3,5…)個の物が並んでいる場合、最初の番号と最後の番号の合計を2で割った答えが真ん中の番号になります。5個並んでいる場合を思い浮かべれば分かります(図1)。
この問題では最初=1で最後=35なので(1+35)÷2＝18より真ん中は18番目と分かります(図2)。
5個の真ん中は(1+5)÷2
35個の真ん中は(1+35)÷2
↓
N=18と分かったので、18番目の数を求めます。
初めの数＝1、公差＝6、N＝18で公式の形を作ると、18番目の数＝1+6×(18-1) となります。
これを計算すると1+6×17＝1+102＝103です。
103
類題1(2)
順番の計算には「番目」ではなく「番差」を使います。9番目=9-1＝8番差です。
まず「真ん中から数えて9番目」が、はじめから何番目の数なのか(Nがいくつか)を求めます
9番目＝9-1＝8番差なので、真ん中(18番目)から9番目は18+8＝26番目になります。
↓
次に26番目の数を求めます。
初めの数＝1、公差＝6、N＝26で公式の形を作ると、18番目の数＝1+6×(26-1) となります。
これを計算すると1+6×25＝1+150＝151です。
151
類題1(3)
これも、まずNを求めます。
後ろから数えて6番目の数は、前に35-6＝29個の数があります。
後ろから数えて6番目の数は、前に35-6＝29個の数があるので、前から数えると、29+1＝30番目になります
後ろから6番目→前には35-6=29個ある→30番目
↓
N=30と分かったので、30番目の数を求めます。
初めの数＝1、公差＝6、N＝30 を公式に入れると、30番目の数＝1+6×(30-1)となります。
これを計算すると1+6×29＝1+174＝175です。
175
爽茶AI作成問題に挑戦！
そうちゃ式AIが自動作成する問題が解けるか挑戦して下さい♪(「始める」を押すと別ウィンドウが開きます)
((作成中))
まとめとプリントダウンロート
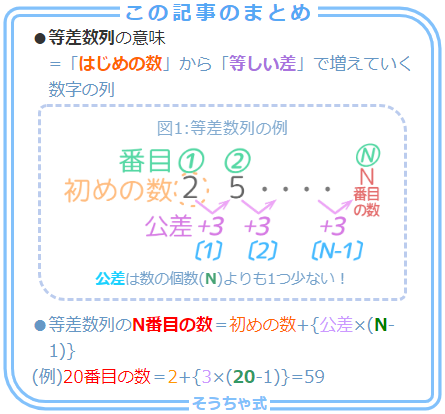
この記事で使った問題の「解答解説」プリントをダウンロードできます。書き込み可能な「問題」プリントはコチラでまとめてダウンロードできます。
無断転載引用はご遠慮ください。
爽茶他の数列の記事も「数列の総合案内」から見て下さい。
●数列だけを解きたい場合、低学年の入門用には「等差数列(上)」
●数列だけでなく算数全体の復習をしたい場合、小4受験生には「算数の基本問題4年」(日能研)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!