中学受験生で「仕事算が苦手！」な方へ。
確かに仕事算は5年で「比」と一緒に出てきて難しく感じることがあります。しかし、仕事算自体は「比」とは関係ありません。
そこで、4年生の方は「比」が出てくる前の先取りとして、５年生の方は一歩下がった基礎固めとして「比なしの仕事算」を学習することをオススメします
「比」無しの仕事算だけを学んでみると意外と簡単でしょうから、その後「比」ありの仕事算を学べばラクに身につけることが出来るでしょう♪
この記事では東大卒講師歴２０年の図解講師「そうちゃ」が「比なしの仕事算」から「比ありの仕事算」まで分かりやすく解説します。
記事を読んで例題を解けば仕事算が苦手では無くなっているでしょう♪
スキマ時間に復習したい人や親塾用に無料プリントもダウンロードもできますよ♪
具体量が示される仕事(受験小4)
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
2023年度の生徒さん募集中です
仕事「算」と聞くと難しそうだと思う人もいるかもしれませんが、別に特別な考え方ではありませんよ。
仕事算の「仕事」
普通、「仕事」と聞くと、お金をもらうために働くことを思い浮かべるでしょう。
しかし、仕事算の「仕事」はお金をもらえるかどうかは関係ありません。
100pの本を読むのも、チョコを20個食べるのも「仕事」です。
つまり仕事算では何かをすることを「仕事」と考えます。
考え方を理解♪
例題に答えながら、仕事算の考え方を理解しましょう
1-1:仕事算の基本
ヒント
気楽に答えて下さい
解答
48枚のクッキーを2枚づつ小さな袋に分けていくのと同じなので、48÷2=24日 ですね。
これが仕事算です。簡単でしょ？
考え方
この場合はクッキー48枚を食べるのが「仕事」です
そして「1日2枚」のような仕事をする(食べる)速さを「ペース」と呼びましょう
仕事を終わらせる(クッキーを食べ終わる)のにかかる時間はそのまま「時間」で良いでしょう。
●「仕事(量)」
→やるべきこと全体の量
●「ペース」
→1時間や1日でする仕事の量
●「時間」
→仕事を終わらせるのにかかる時間
今の問題では「時間」を「仕事(48)」÷「ペース(2個/日)」=24日 と求めました。
解説
48枚を16等分すれば良いので、48÷16＝3 で1日3枚ですね。
これは「ペース」を「仕事(48枚)」÷「時間(16日)」=3枚/日 と求めたことになります。
解説
1日3枚のペースで10日なので、クッキーは3×10＝30枚あったと分かりますね。
これは「仕事量」を「ペース(3枚/日)」×「時間(10日)」=30枚 と求めたことになります
このように、仕事算では3つの数値「仕事(量)」「ペース」「時間」を使って計算を行います。
途中で出てきた3つの数値の関係をまとめると、次のようになります(仕事算の公式)
●仕事(60枚)＝ペース(2枚/日)×時間(30日)
●時間(30日)＝仕事(60枚)÷ペース(2枚/日)
●ペース(2枚/日)＝仕事(60枚)÷時間(30日)
この公式を長方形のような面積図にするとこうなります
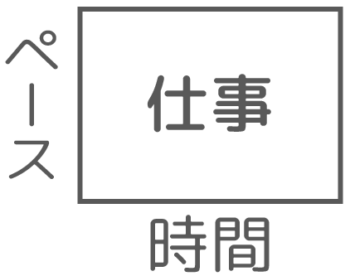
「仕事＝ペース×時間」を「長方形の面積=たてxよこ」にしています
では練習問題をどうぞ
1-1:仕事算の基本
解説
「アメ全部を食べる」のを仕事とすると、仕事量=ペースx時間=4×25=100個
解説
ペース=仕事量÷時間=100÷10=10個/日
ヒント
最後の計算に注意しましょう
解説
2週間=14日間で食べたアメは100-16=84個なので、食べるペースは84÷14=6個/日。
このペースで残り16を食べるのにかかる時間は16÷6＝2余り4より、2日(6個食べる)+1日(4個だけ食べる)=3日
最後の日だけは食べる個数(ペース)が変わってしまいました。
本格的な仕事算ではこの「ペースの変更」が問題になります。
「速さ」との類似
「速さ」を学習した人は気づいたかもしれませんが、「速さ」の公式と似ていますね！(まだ「速さ」を学習していない小4受験生は、関連サイト「そうちゃ式算数2号館」の「速さの基本」で速さの基礎だけ学習しておくとライバルに追いつく/差をつけられますよ♪)
●道のり(12km)＝速さ(4km/時)×時間(3時間)
●時間(3時間)＝道のり(12km)÷速さ(4km/時)
●速さ(4km/時)＝道のり(12km)÷時間(3時間)
「仕事→道のり」「ペース→速さ」「時間→時間」と変えれば同じですね。仕事算は速さの問題とほぼ同じです。
面積図も速さの面積図と似ています。
「仕事=ペースx時間」を「長方形の面積=たてxよこ」の面積図にすると、こうなります
と考えられる
ペースの変更
少し本格的な問題を考えます。途中で仕事のペースを変える場合です
1-2:ペースを途中で変更する
解説
「ペース=仕事量÷時間」に仕事量60枚、時間20分を入れて、ペース=60枚÷20分=3枚/分
解説
はじめの16分にした仕事は3×16=48枚で、残りは60-48=12枚。
それを終えるのに12÷2=6分かかるから全部で16+6=22分
今の様子を面積図にするとこうなります。ペースが変わると高さが異なる長方形が出来て、全体としてL字形になります
L字形の左部分は3枚/日のペースで16分仕事をした量(48)を右の部分は2枚/日のペースで6分仕事した量(12)を表しています。
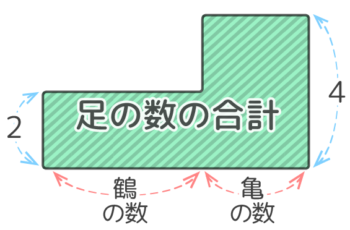
L字形の面積図といえば、つるかめ算の面積図を思い出します(よね？)
実際、解き方もつるかめ算と同じになるのを次の小問で確かめて下さい
解説
つるかめ算と同じように解きましょう
解説
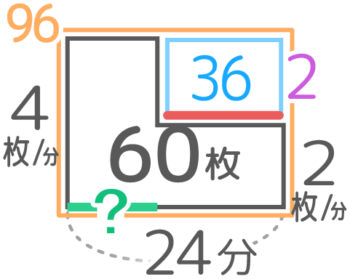
「はじめのペース4,あとのペース2,合計の時間24分、全部の仕事60」を面積図にするとこうなります
この図の「？」をつるかめ算と同じように求めます(解き方が分からない/忘れた人は「L字型の面積図」を見て下さい)
24分全部4枚/分で仕事すると4×24=96枚(大きな長方形)で、実際の仕事との差は96-60=36枚(欠け部分)。
1分ペースを2枚/分に変えると4-2=2(欠けのタテの長さ)減るので、2枚/分で仕事したのは36÷2=18分間(欠けのヨコの長さ)。
変更したのは24-18=6分後と分かります。
この「ペースの変更」が分かれば仕事算の問題を解く準備はほとんど終了といってよいです
ペースを途中で変更した仕事算
→L字形の面積図になる
(例)仕事開始16分後にペースを3から2に変更
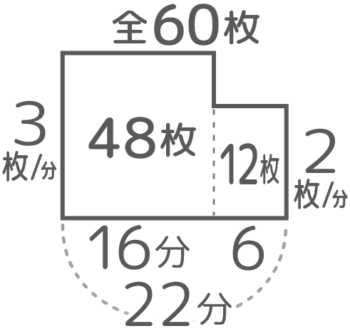
ちなみに、「仕事算」と「速さ」の問題は解き方が似ているので、「速さ」の速度を変更する問題も同様に解けます。興味がある人は関連記事「速さの基本」内の「速さのつるかめ」を見て下さい。
練習問題(2020.6.7作成中)
二人仕事算
1人だけで仕事をするのも寂しいので(笑)、2人以上で「仕事」をする場合を考えてみましょう♪
1-3:何人かで仕事
解説
まず、ABそれぞれのペースを出します。
Aのペースは120÷60=2個/日、Bのペースは120÷40=3個/日 です。
2人が同時に食べるとき、1日に減る量は2+3=5枚/日になります。これが2人分のペースになります。
この5枚/日のペースで120枚のアメを食べるので、時間=仕事(120)÷ペース(5)=24日で食べ終わると分かります。
解説
Aさんが10日で食べる量(仕事)は、ペース(2)×時間(10)=20個で、残りは120-20=100個です。
これを2人で5枚/日のペースで食べるので、100÷5=20日かかります。
全部で10+20=30日かかると分かります。
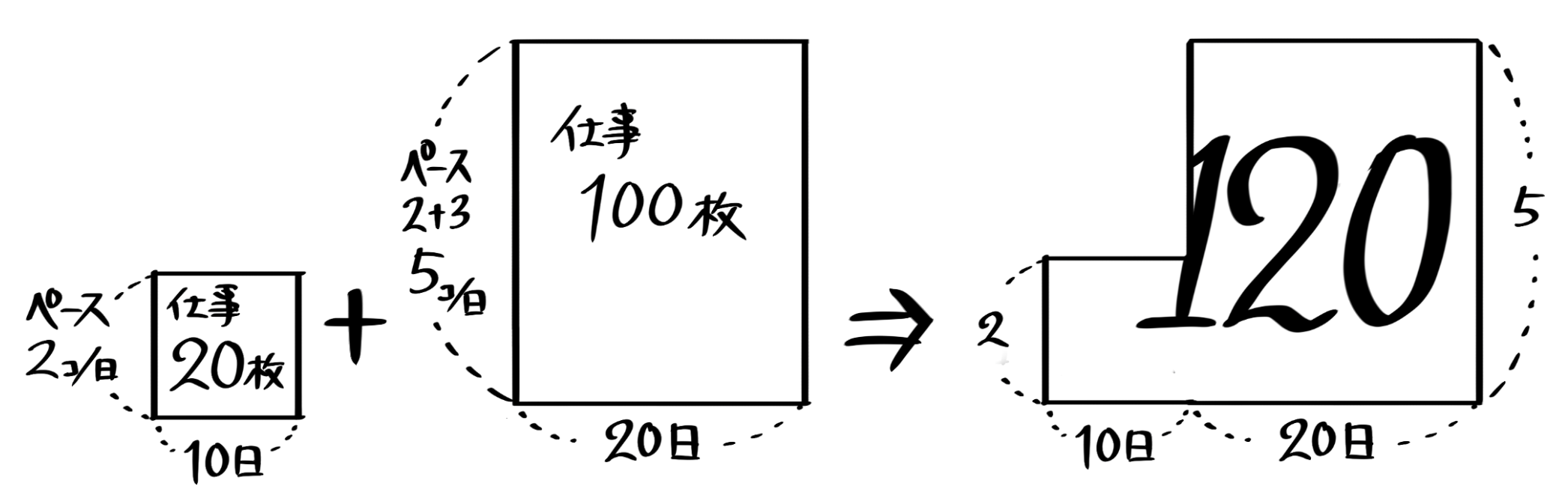
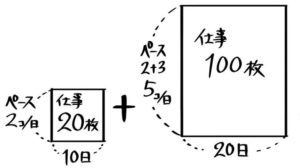
今計算したことは面積図に表すことができます。
最初の10日間は2(タテ)×10(横)=20(面積)の長方形、次の20日間は5×20=100の長方形
合わせると「L字型の面積図」になります。
↓
ということは…
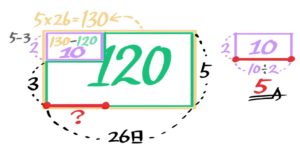
解説
小問(2)の面積図を見て「次はつるかめ算かな」と思った人は鋭いですね！
これは「チョコ3個入りの箱と5個入りの箱があわせて26個あって、中のチョコを出したら120個になった。3個入りの箱はいくつか？」と同じ問題です。
？を出すには、{(26×5)-120}÷(5-3)=5で5日と分かります。
面積図を使わない場合(置き換え法=差集め算)でも計算は同じです。
解き方が分からない/忘れた人は「L字型の面積図」を見て下さい。
このようにある人と他の人の「ペース」は足し算できます。(場合によっては、引き算もできます)
それぞれのペースを合計する
(例1)
製品を1日3個作るAと4個作るBが同時に仕事
→製品は1日に3+4=7個作られる。
(例2)
水を1分で2L汲むポンプCと3L汲むポンプDで
同時に汲み上げる
→水は1分に2+3=5L汲み上げられる。
これで仕事算の基本は終了です。
小まとめ
●3つの公式
・仕事(60枚)＝ペース(2枚/日)×時間(30日)
・時間＝仕事÷ペース
・ペース＝仕事÷時間
●複数人で同時に仕事→ペースを合計
●2人の仕事の合計時間しか分からない場合
→つるかめ算と同じ計算をする(面積図)
具体量が示されない仕事
(受験小4～)
仕事の量が示されていない場合、例えば「Aさんが3時間で終わる仕事」「Bさんが5時間かかる仕事」のような問題を解くには、全体の仕事量を自分で決めないと計算ができません。
ここで2種類の決め方を紹介します。
①仕事全体の量を「1」とする
②仕事全体の量を1以外の整数とする
②の方が簡単なのですが、②が分からないこともあるので、①も出来るようにしておく必要があります。
まずは簡単な②から説明します
仕事全体を1以外の整数とおく
たとえば「Aさん1人だと5日間、Bさん1人だと6日間で終わる仕事」の場合
仕事の全体量を5と6の最小公倍数30とおくと、Aのペース=30÷5=6、Bのペース=30÷6=5 とペースも整数になるので計算が簡単そうですね♪
あとは上と同じように解けばOKです。例題で試してみましょう
2-1-1:仕事を整数とおく
解説
仕事の全体量を10と15の最小公倍数30とおくと、Aのペース=30÷10=3、Bのペース=30÷15=2 で、AB2人で行うペース=3+2=5となる。
よって2人で仕事を終えるのにかかる時間は仕事30÷ペース5=6日
ヒント
途中でペースが変わる→つるかめ算ですね
解説
はじめはB1人でペースは2、途中からA+Bでペースは5、合わせて9日で30の仕事をしたので「仕事のつるかめ算」の面積図にするとこうなります。
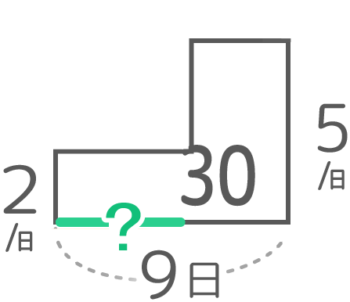
？がB1人で仕事をした日数です。これをつるかめ算の解法で求めると
?(Bが1人で仕事した日数)={(9×5)-30}÷(5-2)=5
練習問題(2022.6.14作成中)
仕事全体を1とおく
一方、仕事を終わらせるのにかかる時間(所要時間)が問題文からはっきり読み取れない場合があります。
例えばこんな問題です
2-2-1:所要時間が不明
こういうときは仕事全体を最小公倍数におけませんが、かわりに仕事全体の量を「1」とおけばペースを計算できます。
さっきの「Aは仕事全体の13を4時間で終わらせ、Bは仕事全体の12を5時間で終わらせる」なら、Aのペースは13÷4=112、Bのペースは12÷5=110 と決まります。
この場合、ペースは分数になるので計算が面倒くさく感じるかもしれませんが、解き方自体は上と同じです。
例題を解いてみましょう
2-2-1:仕事を1とおく
解説
仕事全体を1とおくと、Aのペースは13÷4=112、Bのペースは12÷5=110 と決まるAさん一人で仕事を終えるのにかかる時間は、1÷112=12日、Bさんは1÷110=10日です。
解説
二人同時のペースは112+110=560+660=1160です。
かかる時間は1÷1160=6011=5511日なので、終わるのは6日目(の途中)。
解説
「仕事のつるかめ」です。面積図にすると、L字型全体の面積が1、全体の横幅が11,左(A)の高さ(ペース)が112、右(B)の高さ(ペース)が110です。
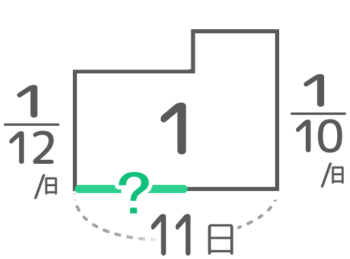
Aが1人で働いた日数「？」を出します。
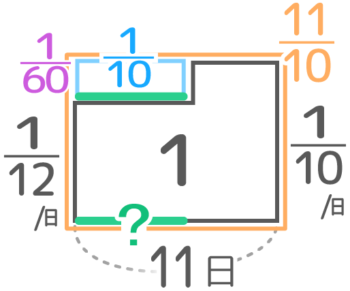
Aの日数は、{(110×11)-1}÷(110–112)=110÷160=6日、Bが11-6=5日と分かります。
確認テスト(2020.6.6作成中)
「具体量が示されない仕事」は以上です。
次は大勢の人で仕事をします
のべ仕事算(帰一算)
ここまでは2人以上で仕事をする場合に「Aさん」「Bさん」というように1人1人に個性がありました=1人1人ペースが違いましたが、個性の無い＝ペースが同じ複数の人間が共同で仕事をする場合があります。
このような仕事算を「のべ」仕事算と呼びます
1種類の人間
3-1:のべ仕事算
無名で個性のない人=ペースが同じ人達が出てくるのがこの問題の特徴です。
普通の仕事算と同じように、まずペースを出してみましょう。
仕事全体が具体的な数値でないので1とおくと、一日の仕事のペースは1÷5=15と求められますが、これは20人が一日でする仕事量です。
1人分の仕事量はこれをさらに人数(20)で割らないといけません。15÷20=1100が1人分の1日のペースになります。
*別解
5×20=100を仕事量にして、1人1日分のペースを100÷5÷20=1としても良い)
このような個性の無い複数の人が働く仕事算「のべ仕事算」では、1人のペースを出す式が「普通の仕事算」より少し複雑になります。
●ペース=仕事量÷時間
(例)A君がある仕事をするのに
20日かかった
→A君の1日の仕事のペース
=1÷20=120
●1人のペース=仕事量÷時間÷人数
(例)ある仕事をするのに
20人が働いて5日間かかった
→1人の1日の仕事のペース
=1÷5÷20=1100
この考えを使って、例題を考えてみましょう
3-1:のべ仕事算
解説
仕事全体を1とすると、1日分1人の仕事のペースは 1÷5÷20=1100です
25人で働くと、1日の仕事のペースは1100×25=14になります。
よって、終わるのにかかる時間は1÷14=4日と分かります。
解説
2日で終わらせるには、1日のペースは1÷2=12が必要
1人の1日のペースは1100なので、1日で12というペースを出すのに必要な人数は12÷1100=50人と分かります。
一応、公式セットを作るとこうなりますが、最初のペース以外は無理に憶えなくてもよいかもしれません。
●ペース=仕事量÷時間
(例)A君がある仕事をするのに
20日かかった
→A君の1日の仕事のペース
=1÷20=120
●仕事量=ペース×時間
●時間=仕事量÷ペース
●1人のペース=仕事量÷時間÷人数
(例)ある仕事をするのに
20人が働いて5日間かかった
→1人の1日の仕事のペース
=1÷5÷20=1100
●仕事量=1人のペース×人数×時間
●時間=仕事量÷(1人のペース×人数)
確認テスト(2020.6.6作成中)
2種以上の人間
上の問題は個性のない1種類の人間でしたが、2種類の人間、例えば大人と子どもがいる場合を考えます
3-2:のべ仕事算(二種類)
さっき解いたのべ仕事算と同様に、1日の1人あたりのペースを出すことからはじめます。
単純に仕事全体を1とすると、大人1人のペースは1÷12÷6=172、子ども1人のペースは1÷18÷10=1180になります。
また、仕事全体を6×12=72と10×18=180の最小公倍数360にすると、大人1人のペースは5、子ども1人のペースは2となります(今回はこちらで解きます)
あとは仕事算標準の解き方でいけるでしょう。
3-2:のべ仕事算(二種類)
解説
仕事全体を6×12=72と10×18=180の最小公倍数360にすると、大人1人のペースは5、子ども1人のペースは2となる。
大人2人と子ども7人のペースは(5×2)+(2×7)=24なので、かかる時間は360÷24=15分
別解
仕事全体を1とすると、大人1人のペースは1÷12÷6=172、子ども1人のペースは1÷18÷10=1180になる。
大人2人と子ども7人のペースは(172x2)+(1180x7)=115なので、仕事が終わるのにかかる時間は1÷115=15分
ヒント
「仕事のつるかめ」ですね
解説
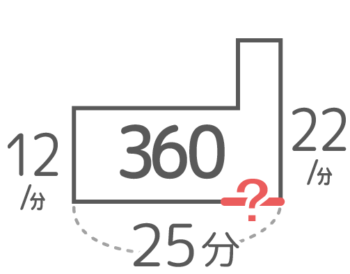
はじめのペースは2×6=12,あとのペースは(2×6)+(5×2)=22です
したがって、はじめのペース12,あとのペース22,合計時間が25分、仕事量360の「仕事のつるかめ算」です
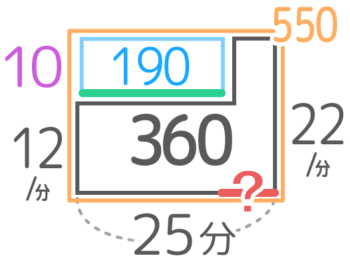
子供だけが働いた時間={(22×25)-360}÷(22-12)=190÷10=19分なので、大人が働いた時間？=25-19=6分間と分かりますね
練習問題(2022/7/5作成中)
場所取り問題
のべ仕事算と同じ方法で解く問題に「場所取り問題」があります。
こんな問題です
3-3:場所取り算
解説
席が3つで時間が40分なので「席に1分座るチケット」が3×40=120枚あると考える
これを5人で平等に分けるので、1人が座る時間は120÷5=24分になる
解説
子どもは1人が2人分なので、大人2人子ども6人の計8人家族で座る考える。
120÷8=15より、大人は15分、子どもは2人分なので15×2=30分座れることになる
練習問題(2022/3/25作成中)
ペースから決める仕事算
(受験小5)
ここまでは仕事の全体量を先に決めてからペースを求めていましたが「比」を学習した後は「速さと比」と同じような関係を利用してペースを先に決めることもできます。
●道のりと速さの比は等しい
●道のりと時間の比は等しい
●速さと時間の比は逆になる
●仕事全体と仕事ペースの比は等しい
●仕事全体と時間の比は等しい
●仕事ペースと時間の比は逆になる
三番目の公式を使って、2人の時間の比などから仕事の比を求め、その数字を元に仕事全体の量を決めます。
直接記述がある場合
仕事全体の記述がある場合
例えば、こんな問題です
X-0-1:ペースから決める
この場合、時間の比が3:4なのでペースの比は逆の4:3と分かるので、Aのペースを④にBのペースを➂とおくことが出来ます
6時間
Bだけで
8時間
ただ、このように仕事全体を基準にする場合は、上の方で使った方法「仕事全体を6と8の最小公倍数24とおいてからペースを出す」でも解けてしまうので、比を使う意味は少ないです。
全体の記述がない場合
一方、全体の仕事量が分からない、こんな問題もあります。
X-0-2:ペースから決める
この場合も、「等しい量から逆比を求める」考え方を使えば、時間比3:4の逆比でAのペースを④にBのペースを➂とおいて
Bが4日働く
「とりあえず」問題を先に解き進めることが出来る♪ので、複雑な問題を解くのに便利です。
ペースそのものが記述されている場合
もちろん、2人の関係が直接的に「AはBの43倍働く」と書いてある場合もAのペース:Bのペース=43:1=4:3 とおくことができますね。
←全体が分からなくても、
割合や比からペースを決められる場合
(例1)Aが3日休んだ分をBが働くと4日間働かなくてはならない
→Aのペースは④、Bのペースは③(逆比)
(例2)AはBの43倍働く
→Aのペースは④、Bのペースは③
では、以上の考え方で例題を解いてみましょう。
X-1:明示のペース先行型
解説
「Aが6日休むとBが5日余分に働かないといけない」の部分で、AのペースとBのペースは6:5の逆比で⑤と⑥と決められます。
解説
「A1人が12日働いたあとB1人が5日働くと完成する仕事」は⑤x12+⑥x5=60+30=90で、
ペース⑤のA1人で仕事をするとかかる時間は90÷⑤=18日です。
解説
はじめAB2人のペース⑤+⑥=11、途中からB1人のペース⑥で全部で10日、仕事量は90なので面積図にするとこうなる
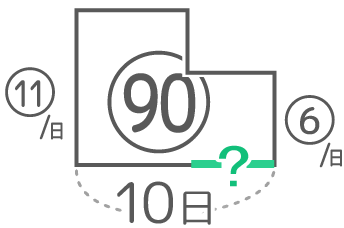
これをつるかめと同様に解くと、?={(11x10)–90}÷(11-⑥)=20÷⑤=4日と分かる
=20÷⑤=4日
練習問題(2022.7.13作成中)
直接記述がない場合
難しいのは、全体の仕事を(最小公倍数などの)数字におくことが簡単にできず、時間やペースの比も書いていない場合です。
例えばこんな問題です。
4-1:黙示のペース先行型
なんとなく「消去算」のような感じがしないでしょうか?(汗)
消去算のように式を2つ作ると「仕事=Ax16+Bx6」と「仕事=Ax10+Bx15」となり、これらは等しいので「Ax16+Bx6=Ax10+Bx15」という関係になります。
これを線分図等にして比べると、Ax6=Bx9が等しいと分かります。
Ax10+Bx15 が等しい
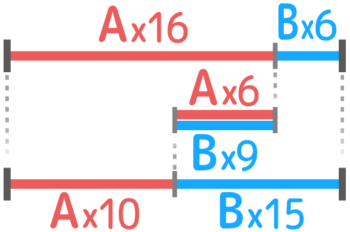
ここから逆比の考えで、AとBのペース(の比)が分かって、このペースを「Ax16+Bx6」に使って仕事全体も分かるので、あとは今までの仕事算のように解けるでしょう。
では解いてみましょう！
4-1:黙示のペース先行型
解説
Aのペースを「A」Bのペースを「B」として仕事全体を2通りで表すと「Ax16+Bx6」と「Ax10+Bx15」になり、この2つは等しいので「Ax16+Bx6=Ax10+Bx15」という関係が分かる
式を観察したり線分図を書いたりして考えると、Ax6=Bx9 と分かる。線分図だとこうなります。
Ax10+Bx15 が等しい
これは「A6日分とB9日分が等しい」ので、6:9=2:3の逆比で、AとBの仕事のペースは③:②と分かる。
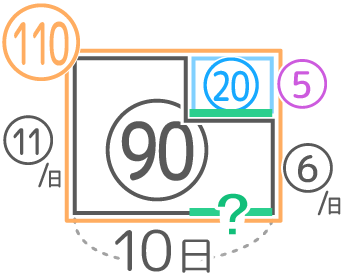
解説
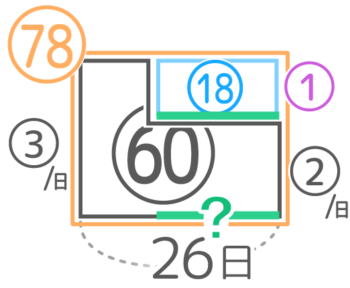
AとBの仕事のペースが③:②と分かったので、これを仕事を表した式「Ax16+Bx6」に使うと仕事全体は③x16+②x6=60となる
60の仕事を、はじめのペース③とあとのペース②の合計26日で完成させる「仕事のつるかめ」になりますね。
Bが働いた日数?={(26x③)–60}÷(③-②)=18÷①=18日なので、Aも26-18=8日と分かりますね♪
すぐ忘れちゃう…という方へ
仕事算は以上です♪理解できましたね？
ただ…一旦理解しても、他の分野を学習している間に記憶が薄れてしまいます。特に算数が苦手な方は「忘れて」しまうのも珍しくありません。
(参考)なぜ「忘れてしまう」のか？
実は、「忘れてしまう」と言っても頭の中から消えるわけではありません
誰でも、何かを学ぶ=新しい知識を「頭の棚」に入れると古い知識はちょっと奥に隠れますが、算数が得意な人は無意識に「頭の棚」を整理して古い知識も取り出せるようにしているので「忘れる」ことがありません。
一方、算数が苦手な人は整理が出来ないまま知識を詰め込むので古い知識はどんどん奥に追いやられ、時間が立つと取り出せくなる=「忘れてしまう」のですね…
だから、算数が苦手な人は、新しく学ぶだけでなく、意識的に頭を整理しないといけません。でも、どうやって整理すればいいのか？それが「復習」なのですね
今まで学んだ知識を広く取り出すことで、知識が取り出しやすいように頭が整理されて「取り出せない！」=「忘れた」ということが無くなっていくのです♪
こういうわけで、算数が苦手な人は新しい知識を学ぶだけでなく、定期的に復習しないといけないのです！
とはいえ、塾や習い事で忙しくて復習の時間がとれないし、復習に何を使えばいいの？。という人も多いでしょう。
そこで東大卒講師歴20年の図解講師「そうちゃ」が生徒さんの復習用に作成している教材を再構成デジタル化して「そうちゃ式 復プリ」として提供します♪(→復プリの紹介記事)
この記事と仕事算の応用「ニュートン算」の記事を合わせて収録しています。
これを定期的に復習しておけば、摸試入試の前に見直すだけで試験中に公式・解法が頭の棚からサッと引き出せるようになりますよ♪
今ならα版特別価格200円！で2022年度内のアップグレード版は無料でダウンロードできます♪
購入はコチラ(購入ページにジャンプします)
まずは体験版を♪
「復プリ」なんて聞いたこともない…効果あるの？という方や3・4年生の方向けに無料の体験版を用意しました！
この記事の仕事算の問題/解説プリント3枚をご利用いただけます。著作権は放棄しておりません。無断転載引用はご遠慮下さい。
ダウンロードにはパスワードが必要です。こちらからDL登録すると、このページ共通のパスワードを自動返信メールで受け取れます。
*「パスワードを入れてもダウンロードできない」という方はブラウザや使用機種を変えて再度お試し下さい
オススメ教材
爽茶●仕事算だけを解きたい場合は「仕事算」(中学入試まんが攻略BON)
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題」シリーズ(日能研)
●小6受験生には「算数ベストチェック」(日能研)
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!