中学受験生で「ニュートン算て何？！」という小4の方から「ニュートン算習ったけど全然分かんない…」という小5・小6の方へ
確かに「ニュートン」という名前！が難しそうで、解答に使う理屈もやや複雑なので苦手な人が多いんです…
でも、他の特殊算と同じように問題のパターンは限られていて(3つとちょっと)、5年までにそのうち2つができれば大丈夫です(残りのパターンは入試までの間にできるようにすればOK♪)
2つのパターンを出来れば良いと考えると気がラクになりませんか？(なりましたよね)
塾で習っても分からなかった人は「塾の教え方が悪かったんだ」と思って、この記事で学びなおしましょう！
この記事では東大卒講師歴20年の図解講師「そうちゃ」がニュートン算の基礎から応用問題まで分かりやすく解説します。
記事を読んで例題を解けばニュートン算が得意になっていることでしょう
ニュートン算とは
ニュートン算は○○算の一種
さっそくニュートン算の基礎問題を見て下さい(見るだけでいいですよ♪)
0-1:ニュートン算(基礎)
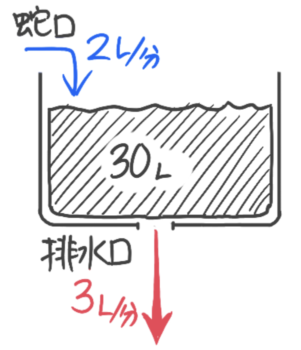大きな水そうがあります。この水そうの底には排水口が2つあり、それぞれ毎分3Lの水を出します(始めは２つとも閉まっています)。この水そうに蛇口から毎分2Lの水を入れていき、30Lの水がたまったところで、蛇口を開いたまま排水口を1つ開きます。何分で水がなくなりますか？これがニュートン算の基礎問題で、溜まった水を減らすという「仕事算」です。
つまりニュートン算は仕事算の一種です。
ちなみに仕事算の公式はこうでした。
(例)50個のクッキーを10日で食べる「仕事」
→仕事の量は50個。時間は10日。
→食べるペースは50÷10=5個/日
●仕事量(50)＝ペース(5)×時間(10)
●時間(10)＝仕事量(50)÷ペース(5)
●ペース(5)＝仕事量(50)÷時間(10)
忘れたという人は参考記事「仕事算まとめ」を読んで下さい。
「差し引き」でペースを決める
さっきの問題をもう一度
0-1:ニュートン算(基礎)
解説
この問題では単純に水を減らすのではなく、「水を入れながら出す」というプラスとマイナスの仕事を同時に行っています。
仕事算の応用問題で、プラスとマイナスが同時に行われている場合に「差し引き」の考え方を使いました。
仕事算の一種であるニュートン算でも、この差し引きの考えを使います。
この問題で差し引きの考えを使うと「2Lの水を入れながら3Lの水を出すのは3-2=1Lの水を出すのと同じ」と言えます。
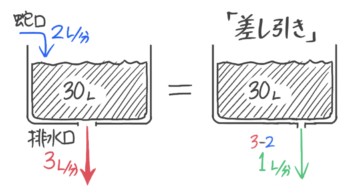
「1L/分で排水する」のと同じ
つまり、この問題での水が実際に減るペースは1L/分ということです。
よって30Lの水を全部出すのには仕事算の公式「時間=仕事量÷ペース」で30÷1=30分かかると分かります。
このように、ニュートン算は実際のペースが単純に決まらず「差し引き」をしないといけません。
→「増やすペース」と「減らすペース」を
「差し引き」して決める
(例1)2L/分で注水しながら3L/分で排水する
→水が実際に減るペースは差し引き3-2=1L/分
(例2)毎日100円貯金するが、毎日30円づつ使う
→お金が実際に増えるペースは差し引き100-30=70円/日
今度は排水口を2つ開いてみましょう
0-2:ニュートン算(基礎)
注意
排水口の数が2つ(2倍)になれば、空になる時間は半分のような気もしますが…
解説
さっきと同じ差し引きの考え方を使います。
2L入れながら3×2=6L出すので、実際には差し引き6-2=4Lの水を出すのと同じです。
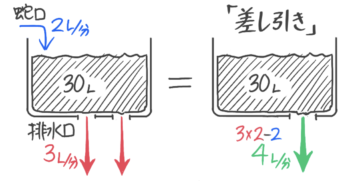
「4L/分で排水する」のと同じ
水そうが空になるのは30÷4=7.5分後=7分30秒後です。
始めの場合と比べると、排水口の数は2倍になったのに、水の出し入れを差し引きした結果は「3-2=1」から「(3×2-2)=4」で4倍にもなっています！
もし排水口が3つあったら差し引きの結果は(3×3)-2=7で7倍に、4つあったら(3×4)-2=10で何と10倍に！なります
→「増やすペース」と「減らすペース」(いくつかあることも)
を「差し引き」して決める
(例1)2L/分で注水しながら3L/分の排水口2つで排水
→水が実際に減るペースは差し引き(3×2)-2=4L/分
(例2)2L/分の蛇口2つで注水しながら、
3L/分の排水口3つで排水
→水が実際に減るペースは差し引き(3×3)-(2×2)=5L/分
○○算との違い～3つのキー
このように溜まっているモノを「差し引き」のペースで減らしてゼロにするのが「ニュートン算」です。
ここまででニュートン算には重要な3つの数字が出てきました。
①最初の量(溜まっていた水)
②増やすペース(1つの蛇口の注水ペース)
③減らすペース(1つの排水口の排水ペース)
で、これらを「3つのキー(key:鍵)」と呼びましょう。
ニュートン算の基礎問題では、この3つのキー全てが分かっていたので、仕事算とあまり変わりませんでしたが、この後の問題では3つのキーのうち分からないものを求めること自体が問題になります
→仕事算の一種で、
差し引きしたペースで減らしていく問題
●出てくる3つのキー
➀最初の量(溜まっている水)
➁増やすペース(蛇口から注水)
③減らすペース(排水口から排水)
★普通は3つのキーのどれかが分からず、
まずそれを求めないといけない
●「実際のペース」はキー②とキー③の差し引きで決める
(例)2L/分の蛇口4つで注水しながら、
3L/分の排水口5つで排水
→水が実際に減るペースは差し引き(3x5)-(2×4)=7L/分
●ニュートン算の公式(仕事算改)
・実際のペース=③減らすペースx個数-➁増やすペースx個数
・時間=最初の量÷実際の実際のペース
爽茶これでニュートン算の仕組みが分かりましたね♪
けっこう簡単でしょう？
・1つが分からない場合を「基本」
・2つが分からない場合を「標準」
・3つとも！分からない場合を「応用」
という分類で、問題を解いていきます。
ニュートン算(1)基本問題
基本問題は3つのキー「 ①最初の量 ②増やすペース ③減らすペース 」のうち1つ(普通は③)が分からない場合、例えばこんな問題です
1-1:ニュートン算(基本)
①最初の量＝60,②増やすペース=3とわかりますが③減らすペースが分かりません。
仕事算の延長として解く
まずは慣れた仕事算として解いてみましょう
1-1:ニュートン算(基本)
解説
仕事算の公式「ペース=仕事÷時間」を使うと、60÷4=15 で実際に減るペースが15L/分と分かりますが、この実際のペースは1分間で注水される量(3L)と排水される量の差し引きの結果です。
つまり、1つの排水口から出る水の量を□とすると、
「(□×2)–3=15」
が成り立ちます。この逆算を解けば、排水口1つが排水する量は □=9L/分と分かります♪
以上の解き方で基本問題は解けるのですが、この後の標準・応用問題ではキツくなります。
そこで「関係式(線分図)を使った解き方」もマスターしましょう。
計算は同じですが難しい問題にも対応でき、標準的な入試問題なら余裕で解けます♪
線分図を使って解く
さっきの例題を少しだけ改造した問題を解いてみましょう
1-1:ニュートン算(基本)
解説
①最初にあった水は60L(最初の量) です。
また、②4分間で蛇口から出た水の量は3×4=12L(増やした量)
さらに③排水口から出た合計は□×2×4=8(減らした量)
この①②③の間には
③減らした量=①最初の量+②増やした量
の関係が成り立ちます。
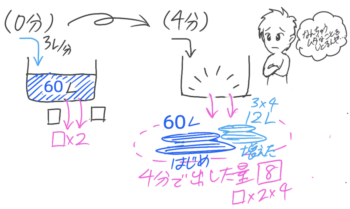
この問題では「8=60L+12L」になります。これを線分図にするとこうなります。
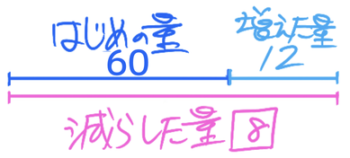
あとは分配算の要領で8=72→1=9L と分かります。
解説
3つのキーである最初の量(60),増やすペース(3),減らすペース(9)がすべて分かっているので、あとは差し引きの仕事算として解きます。
排水口を3つにすると、減らすペースは9×3=27L/分になります。
ここに毎分3Lの水を注ぐので、差し引きして27-3=24が実際に減るペースと分かります。
したがって、水が無くなるのにかかる時間は60÷24=6024=212分=2分30秒です
このように、3つのキー全てが分かるまでは線分図を書き、3つのキーが分かったら仕事算で解く、というのがニュートン算を解く流れになります
●3つのキー
①最初の量 ②増やすペース ③減らすペース
●3つの量(空になるまでの時間=T)
➊最初の量(①そのもの)
❷増やした量(②増ペース×T)
❸減らした量(③減ペース×T)
●3つのキー・量の関係
❸減らした量=➊最初の量+❷増やした量
(③減ペース×T)=①最初の量+(②増ペース×T)
練習問題をどうぞ
練習問題1(2022.6.15作成中)
増やすペースが分からない場合
練習問題2(2022.6.15作成中)
はじめの量が分からない場合
ニュートン算(2)標準問題
ニュートン算の3つのキー「①最初の量②増やすペース③減らすペース」のうち2つ(普通は②と③)が分からない、こんな問題です
2-1:ニュートン算(標準)
3つのキーのうち①最初の量だけが書いてあり、②増やすペースと③減らすペースは分かりません
特徴は、2つの場合が書いてあることで、この2つの場合について3量の関係式「❸減らした量=➊最初の量+❷増やした量」を作るのが、解答の第一歩になります。
では、解いてみましょう
2-1:ニュートン算(標準)
方針
ニュートン算の3つのキー・量の関係を使います
❸減らした量=➊最初の量+❷増やした量
(③減ペース×T)=①最初の量+(②増ペース×T)
解説
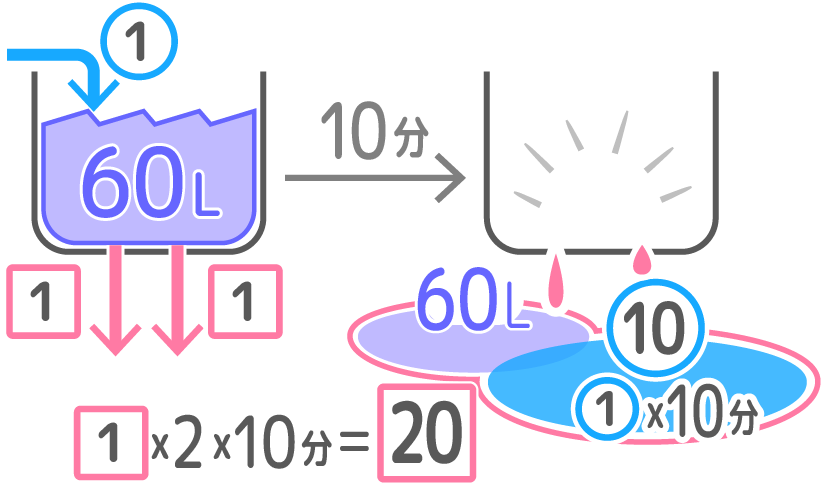
この問題では、2つの場合が書いてあるので、注水ペースを①、排水口1つの排水ペースを1として、それぞれで「(③減ペース×T)=①最初の量+(②増ペース×T)」の関係式を作ります。
まずA:T=10分で空になった場合
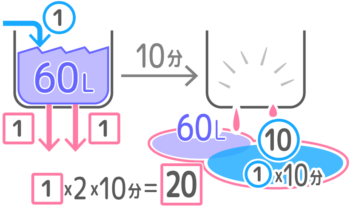
と溜まっていた60L+10分で注水した量⑩が等しい
この図を見て「(③減ペース×T)=①最初の量+(②増ペース×T)」の式を作ると「1×2個×10分=60+(①×10分)」になり、整理すると「20=60+⑩」ができます。
もう一方のB:T=6分で空になった場合は
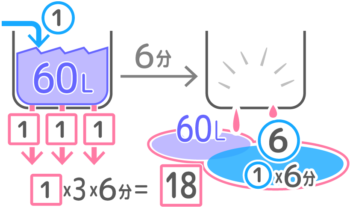
と溜まっていた60L+6分で注水した量⑥が等しい
式を作ると「1×3個×6分=60+(①×6分)」で、整理すると「18=60+⑥」になります
整理した2つの式を並べるとこうなります。
A:20=60+⑩
B:18=60+⑥
2つをあわせて線分図にするとこうなります。
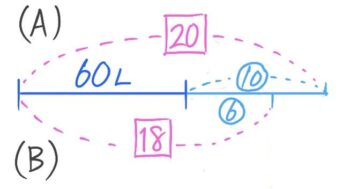
3つの量の関係を1つの線分図に合わせる
この線分図のオレンジ色の部分は④=2の関係になっているので、②=1と分かります。
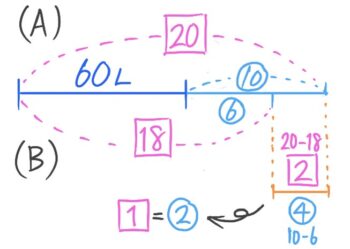
これで□を○で表すことができるので、○に書き換えます
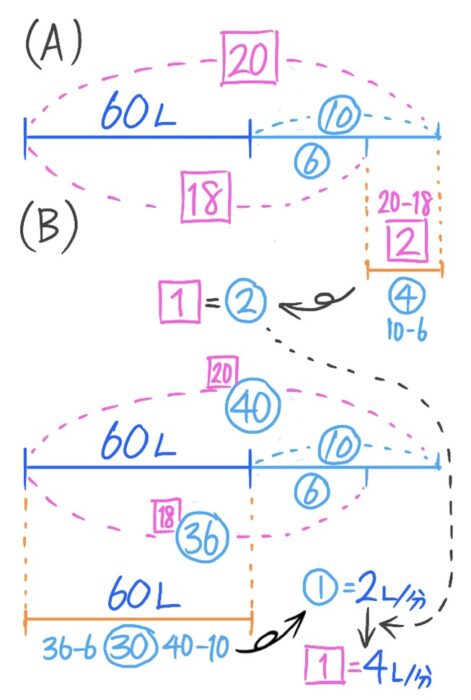
すると、60L=㉚なので①=2,1=4と分かりました。
別解
線分図が苦手な場合は
A:20=60+⑩
B:18=60+⑥
これを消去算にして解いても良いでしょう
Aの式とBの式の差を出すと「2=④」になるので、全体を÷2して「1=②」と分かります。
これを20倍した「20=㊵」をAの式に入れると「㊵=60+⑩」になるので㉚=60から①=2、1=②=4と分かります。
このように、2つのキーが分からない標準問題には2つの文章があるはずなので、それぞれを関係式にして線分図か消去算にして分からないキーを求めれば良いのです。
練習問題1
キー1と2が分からない場合
練習問題2
キー1と3が分からない場合
ニュートン算(3)応用問題
ニュートン算の3つのキー ①最初の量②増やすペース量③減らすペース の全部が!分からない場合です
3-1:ニュートン算(応用)
溜まっている水、注水ペース、排水ペースの全部が分かりませんね
標準問題と同様に2つの場合の関係式を作って比べてみましょう
3-1:ニュートン算(応用)
ヒント
注水ペースを1、排水口1つのペースを1として
排水した量=溜まっていた水(溜)+注水した量 の式を2つ作りましょう
解説
排水口を1つ開いた場合の関係は「1つの排水口で36分で排水した量=溜まっていた水+36分で注水した量」です。
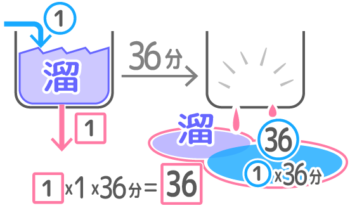
溜まっていた水+36分注水した量㊱が等しい
この関係を式にすると、1x1x36=溜+①x36
整理すると、36=溜+36(この式をAとします)
排水口を2つ開いた場合の関係は「2つの排水口で9分で排水した量=溜まっていた水+9分で注水した量」です
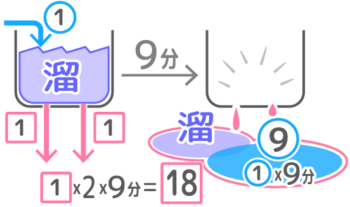
溜まっていた水+9分注水した量⑨が等しい
これを式にすると 1x2x9=溜+①x9
整理すると 18=溜+9(式Bとします)
式Aと式Bを見比べます。
36=溜+36(式A)
18=溜+9(式B)
「消去算」を思い出して差を出すと18=27 と分かりますね？
「＝」の左右ともに÷18すると1=1.5なので排水ペースは注水ペースの1.5倍(または112倍)と分かりました。
次にBの式「18=溜+9」の18の代わりに18x1.5=27を入れると27=溜+9より、溜=18で、溜まっていた水は注水ペースの18倍と分かりました！
これで、注水ペース、排水ペース、溜まっていた水 の比が「①:1.5:18」と分かったので、後は差し引きの仕事算として解けますね♪
ヒント
まず「(差し引きした)実際のペース」を出しましょう
解説
3分以内に空にするためには、差し引きした実際に減るペースが18(溜)÷3=6以上は必要。
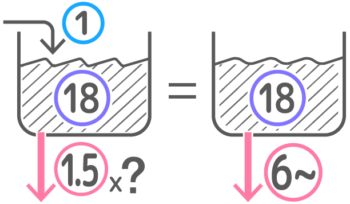
排水口の数を？とすると「(1.5x？)-1=6」
これを逆算で解くと?=4.～(4と5の間)なので4個では足りず、最低5個は排水口を開ける必要があると分かりました！
練習問題をどうぞ(2022.6.16作成中)
応用問題は以上です。
いろいろな具体例
爽茶問題文に出てくる数値のうち、3つのキー①最初の量 ②増やすペース ③減らすペース にあたるのはどれかが分かれば計算は全く同じです。
問題文を読みながら「処理した量=最初の量+増えた量」という式(線分図)を書いていきましょう
泉の問題
底から水が湧き出ている「泉」の水をポンプで汲み出して空にする場合。
3つのキーは、①最初の量=泉に溜まっていた水、②増やすペース=泉の底から水が湧き出るペース、③減らすペース=ポンプ1台で水をくみ出すペース です。
3つの量については次の関係が成り立ちます
❸くみ出した水=➊溜まっていた水+❷湧き出た水
(③減ペース×T)=①最初の量+(②増ペース×T)
例題(基本)
例題(標準)
例題(応用)
行列の問題
ニュートン算で一番有名なのはコレでしょう。
映画館で入場開始時に行列ができていて、入場開始後にも人が並んでいくとき、行列はいつなくなるかという問題
3つのキーは、①最初の量=入場開始時の行列の人数、②増やすペース=行列に人が加わるペース、③減らすペース=窓口1つで人を入場させるペース です。
3つの量の関係は次のようになります
❸入場させた人数=➊最初の列の人数+❷加わった人数
(③入場ペース×T)=①最初の列の人数+(②加入ペース×T)
例題(基本)2020.6.16作成中
例題(標準)
4-2-2:行列ニュートン(標準)
ヒント
2つの場合から関係式を2つ作りましょう
解説
行列の人数を①、1つの窓口から1分間に入場させる人数を1とする。
「入場窓口を1つ開けると5分で行列が無くなり」から、「5分で入場させた人数=入場開始時の行列+5分で加わった人数」という関係ができます。
これを式にすると、1x5=①+4×5 で、整理すると5=①+20 です(式Aとする)
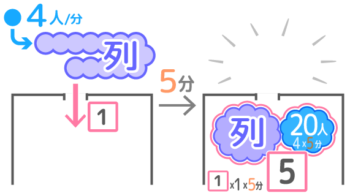
同様に「窓口を2つ開けると2分で無くなる。」から、「2分で入場させた人数=入場開始時の行列+2分で加わった人数」という関係ができます。
これを式にすると、1x2x2=①+4×2 で、整理すると4=①+8 です(式Bとする)
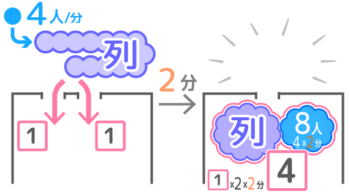
式AとBを(線分図を書いたりして)見比べると、
5=①+20(A)
4=①+8(B)
1=12 と分かります。つまり1分間に1つの窓口から入場させる人数は12人です。
さらに式Bの4の代わりに12×4=48を入れると、48=①+8 という式が出来て、①=40(開始時の行列)と分かります
これで、開始時の行列40人、列に加わるペース4人、入場させるペース12人と3つのキー全部が分かりました♪
ヒント
まず差し引きしたペースを決めましょう
解説
100人の行列を3分でなくすには差し引きして100÷3=33.3…のペースが必要です。
窓口を？個開けるとすると、差し引きのペースは(12x?)-4 なので、(12x?)-4が33.3…より大きくないといけない。
(12x?)-4=33 の逆算を解くと、?=3.~ なので、窓口3つでは足りずに4つ開ける必要があると分かります。
練習(応用)2020.6.16作成中
牧草の問題
すでに草が茂っていて引き続き草が生えてくる牧場に牛を放って草を食べてもらうと、いつ草がなくなるかという問題で、応用問題の例として問題集によく載っています。
3つのキーは、①最初の量=放牧開始時に茂っていた草の量、②増やすペース=1日に草が生えるペース、③減らすペース=牛1頭が1日に草を食べるペース です。
3つの量の関係は次のようになります
❸牛が食べた草=➊最初に茂っていた草+❷新たに生えた草
(③食べるペース×T)=①茂っていた草+(②生えるペース×T)
練習(基本)
練習(標準)
応用問題もどうぞ
4-3-3:ニュートン(牧場)
ヒント
2つの事例から2つの関係式を作りましょう
解説
牛1頭が一日で草を食べるペースを①、草が生えるペースを1、茂っていた草を「茂」として「❸牛が食べた草=➊最初茂っていた草+❷新たに生えた草」関係式を2つ作る
「11頭放して草を食べさせると30日で草が無くなる」
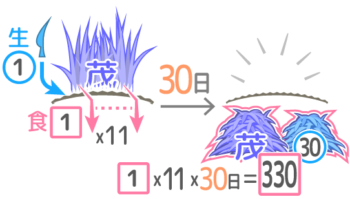
→「①x11x30=茂+1x30 」で整理すると「330=茂+30」(式A)
「21頭放すと10日で草が無くなる」
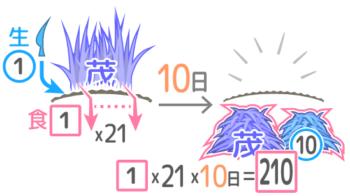
→「①x21x10=茂+1x10 」で整理すると「210=茂+10」(式B)
式AとBを見比べて…
330=茂+30(式A)
210=茂+10(式B)
差をとると120=20
全体を÷20して「6=1」つまり、草が生えるペースは牛1頭が1日に食べる草の6倍と分かります
さらに「6=1」より1の代わりに6を式Bに入れると「210=茂+10」→「210=茂+60」となるので「茂=210–60=150」つまり茂っていた草は牛1頭が1日に食べる草の150倍と分かりました。
ヒント
「差し引きペース」を出しましょう
解説
草が生えるペース1=6なので(差し引きした)実際に草が減るペースは①x16-6=10で、茂っていた草は1=150です
よって草が無くなるのにかかる時間は、150÷10=15日です
ヒント
まず「差し引きしたペース」を出しましょ
解説
150÷7=21.~ が必要な(差し引きした)ペース
?頭を放つとして差し引きしたペースは?–6 なので、?–6=21.~ という逆算を解くと?＝27.~
つまり27頭だと足りず、28頭放つ必要がある
すぐ忘れちゃう…という方へ
ニュートン算は理解できましたね？
ただ…一旦理解しても、他の分野を学習している間に記憶が薄れてしまいます。特に算数が苦手な方は「忘れて」しまうのも珍しくありません。
(参考)なぜ「忘れてしまう」のか？
実は、「忘れてしまう」と言っても頭の中から消えるわけではありません
誰でも、何かを学ぶ=新しい知識を「頭の棚」に入れると古い知識はちょっと奥に隠れますが、算数が得意な人は無意識に「頭の棚」を整理して古い知識も取り出せるようにしているので「忘れる」ことがありません。
一方、算数が苦手な人は整理が出来ないまま知識を詰め込むので古い知識はどんどん奥に追いやられ、時間が立つと取り出せくなる=「忘れてしまう」のですね…
だから、算数が苦手な人は、新しく学ぶだけでなく、意識的に頭を整理しないといけません。でも、どうやって整理すればいいのか？それが「復習」なのですね
今まで学んだ知識を広く取り出すことで、知識が取り出しやすいように頭が整理されて「取り出せない！」=「忘れた」ということが無くなっていくのです♪
こういうわけで、算数が苦手な人は新しい知識を学ぶだけでなく、定期的に復習しないといけないのです！
とはいえ、塾や習い事で忙しくて復習の時間がとれないし、復習に何を使えばいいの？。という人も多いでしょう。
そこで東大卒講師歴20年の図解講師「そうちゃ」が生徒さんの復習用に作成している教材を再構成デジタル化して「そうちゃ式 復プリ」として提供します♪(→復プリの紹介記事)
今回は、この記事と前提になる「仕事算」を合わせて収録しています。
これを定期的に復習しておけば、摸試入試の前にサッと見直すだけで試験中に公式と解法が頭の棚からサッと引き出せるようになりますよ
購入はコチラからどうぞ
オススメ教材
爽茶分かりやすい！と評判のスタディサプリにもニュートン算の授業動画(5年(応用)27回)がありますよ。今なら14日間無料。
興味がある人は「先取りや予習・復習に！ スタディサプリ そうちゃ式のオススメ利用法」へ
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題」シリーズ(日能研)
●小6受験生には「算数ベストチェック」(日能研)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!