「差集め算」が分からない!とお悩みの中学受験生の方へ
確かに「差集め算」は線分図の系統の問題の最終段階なので、けっこう難しいです…が、実は「解き方のコツ」はたった1つしかありません!
「線分図を書いて「ある2つの部分」を比べる」これだけ!
もちろん、線分図の集大成なので書くのが面倒くさい問題もあります。ですが、ここをマスターすれば大抵の入試問題の線分図にも歯が立つようになるので、志望校合格可能性を上げるために頑張る価値はありますよ!
この記事では東大卒講師歴20年の図解講師「そうちゃ」が「ある2つの部分」は何なのか、色々な差集め算を解ける図を見せながら分かりやすく説明します。
記事を読みながら真似して線分図を練習すれば、読み終える頃には「差集め算」が苦手ではなくなっているでしょう♪
四谷大塚「予習シリーズ」を使用している方は予シリを解説した「ヨリシス」シリーズを御覧ください
差集め算の基礎
 爽茶
爽茶「差を集める」考え方
20人の生徒に鉛筆を9本配るとき(計画A)と7本づつ配るとき(計画B)の必要な本数の差は何本でしょうか?
単純な考え方
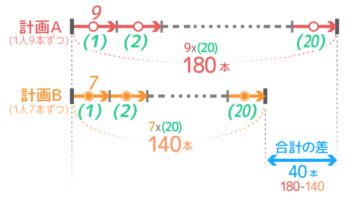
普通は、計画Aでは9×20=180本必要、計画Bでは7×20=140本必要なので、差は180-140=40本と「引き算」で求めますね。
線分図にすると下のようになります
これで大正解なのですが、チョット違う求め方もあります。それが「差集め」です
「差を集める」考え方
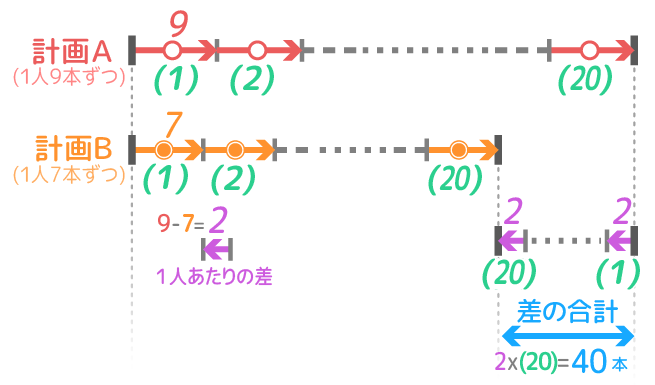
計画AとBで配る鉛筆の1人あたりの差は9-7=2本。20人に配ると、この差2本が20人分集まって20×2=40本。これが本数の差と分かります。
線分図にすると下のようになります
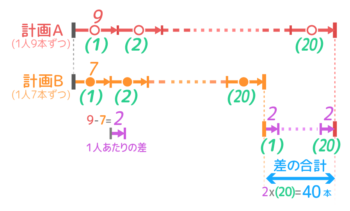
最初のやり方と違って、計画ABそれぞれの合計を出していません。
1人あたりの差を人数分あつめて、差の合計を求める
これが「差集め」の考え方です。
(例)20人の生徒に鉛筆を7本配った時(A)と
9本づつ配った場合(B)の必要な鉛筆の本数の差
○単純な考え方(かけ算→引き算)
9×20-7×20=180-140=40本
●「差を集める」考え方(引き算→かけ算)
1人に配る本数の「差」は9-7=2本
この差を20人分集めて…
→合計の違いは2×20=40本
差集め算の基本図
もう一度、線分図を見て下さい(図を詰めて字を大きくしてあります)。これが「差集め算の基本図」です
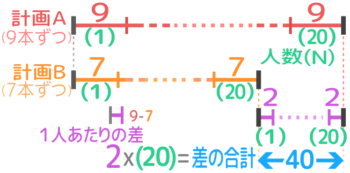
間の長さが差の合計になる
計画AとBの線分図は長さ9と7の小さな「区切り」が20個つながったもので、それぞれ最後の(20)番目の区切りの右端が太くしてあるのに注目です。この2つの太い区切りの間の長さが「差の合計」を表しています。
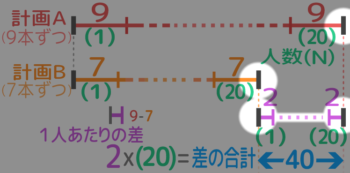
「同じカッコ数字(この場合は20)の区切りを太くして差を見つける」というのが差集め算の基本なので必ず憶えて下さい。
練習してみましょう(ノートなど紙に書いて!)
0:差集め算の基本図
解説
7人ずつ座る計画Aと5人ずつ座る計画Bの線分図を書き、(6)の右端の区切りを太くします。
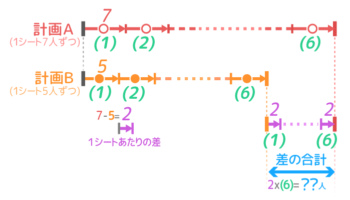
太くした区切りの間の長さ(青い矢印)が差の合計=座った人数の増加分になります
1シートの差=2人、シートの個数=6 なので、差の合計=2×6=12人と分かります。
分かりましたか?
面積図にもできる
差集め算は面積図にもできます。
合計個数の面積図
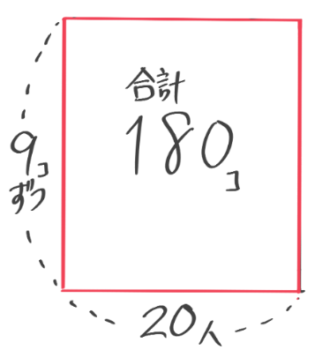
「合計個数=1人に配る個数 x 人数」という関係を「長方形の面積=縦x横」として表現します。
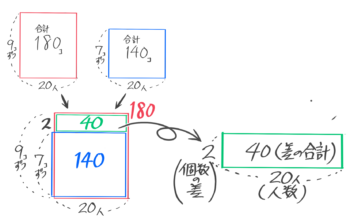
差集め算の面積図
「9本ずつ20人に合計180本配る」と「7本ずつ20人に合計140個配る」2つの面積図を重ねて、1人にくばる個数の差9-7=2と合計の差180-140=40を書き込むと
2つの面積図の間に差集め算の面積図(差集め算の公式:1つの差x人数=差の合計)ができているのが分かります♪
線分図と面積図どちら?
では線分図と面積図どちらを使うのが良いかというと…
解ければどちらでも良いのですが、線分図が長さしかない「1次元」の図であるのに対して、面積図は幅と高さがある「2次元」の図なので、面積図の方が書くのが難しいのです。
ですから、学習が進んで複雑な条件の問題が出てくると、面積図では表すのは難しくなってきます。
従って「差集め算」の基本解法は線分図にしておくのが良いでしょう。
差集め算の基本問題
 爽茶
爽茶差集め算の三公式
上で使った「差の合計=1個(人)あたりの差×個(人)数」という関係式から公式を作ると次のようになります。
●差の合計=1個あたりの差×個数(N)
○個数(N)=差の合計÷1個の差
○1個の差=差の合計÷個数(N)
2番目の公式を一番使いますが、1番目の公式だけを憶えて逆算で2番目・3番目を出しても良いでしょう。
「基本図」と並べるとこうなります。
「N」というのは人数が分からないときの「?」のようなものです。(「X」でもなんでも良いのですが、「そうちゃ式」では「N」にします)
たいていの場合は2番目の式でNを求めますが、一番上の式だけを覚えておいて「?」を入れて式を作って逆算で解いてもOKです。
この基本図と三公式を使って問題を解きましょう
差集め算の基本解法
二段階で求める
1:差集め算(基本)
解説
計画AとBの線分図を書きます。人数が分からないので最後の区切りには(N)と書いて右端は太くします。
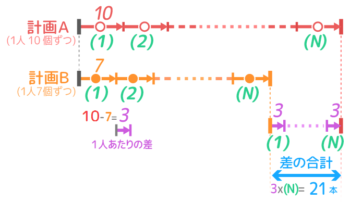
そして太くした区切りの間の長さを線分にします。これが差の合計=21になります。
差集め算の公式「差の合計=1人あたりの差×人数(N)」と1人に配る個数の差が10-7=3を合わせると
「21=3xN」という関係ができるので、N=21÷3=7人と分かります♪
解説
はじめの計画(B)の線分図全体の長さを求めます

計画Bの線分図は長さ7の区切りがN個つながっていて、(1)でN=7と分かったので、計画B全体の長さは 7x7=49個 と分かります♪
このように、Nを求めてから計画AかBの合計を求めるのが差集め算の基本問題です(どちらかしか聞かれない場合もあります)。
分かりましたか?次は誘導無しでどうぞ
練習で定着♪
1:差集め算(基本)
解説
例題の数字変え問題。まず生徒(N)を求めます
一人の差=4本、差の合計=104個なので「104(差の合計)=4(一人の差)xN(人数)」になり、生徒の人数(N)=104÷4=26人
26人の生徒に12本ずつ配るので必要な鉛筆は 12×26=312本 と分かりました。
解説
問題を読みながら線分図を書くと、部屋数(N)は9、差の合計=36人と分かっていますが、1部屋の差(D)が分からないのに気づきます。
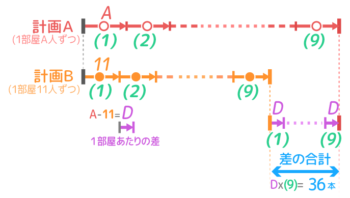
「差の合計36=1部屋の差(D)x部屋数9」なので、1部屋の差(D)=差の合計(36)÷部屋数(9)=4人と分かります。
したがって、今日の1部屋あたりの人数は11+4=15人と分かります
(この問題は計画AやB全部の長さを聞かれませんでした)
基本の差集め算は以上です♪
個数の異なる(不揃いの)差集め算
基本の差集め算が出来るようになったので、少し応用です
個数がそろっていない…
例えば
「妹が1個65円のペンを何本か買い、姉は80円のペンを妹より2本多く買った。」
とか
「リンゴをちょうど8個買える金額を用意して買い物に行った、気が変わって40円高い洋梨を買うことにしたところ6個買えて20円余った。」
のように買った個数(N)が揃っていない場合はどうすれば良いでしょうか?
この場合も線分図等を利用して同じ「N」同士を比ると簡単に解けます
2つの問題のタイプ
①Nを求める問題
②一方の単価を求める問題
があるので順に見ていきます。
Nを求める問題
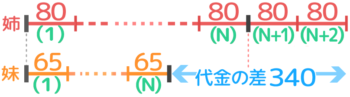
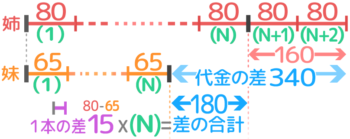
妹は65円の鉛筆を何本か買い、姉は80円の鉛筆を妹より2本多くかったところ代金が340円高くなった。妹は何本買ったか?
少ない妹の本数を「N」にして姉は「N+2」とします。姉の線分図は(N)で終わらずに(N+1)(N+2)まで続けます。
姉妹の(N)の右端の間の大きさが差の合計です。
340-160=180円と分かる。
1個の差は80-65=15円なので、本数(N)=180÷15=12本
一方の単価を求める問題
例題
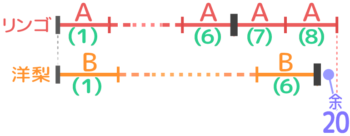
リンゴをちょうど8個買える金額を用意していたが、気が変わって40円高い洋梨にしたところ6個買えて20円余った。リンゴは1個何円か?
個数(N)が全部書いてあるのが特徴です。
まずリンゴと洋梨の線分図を描きます。少ない方の個数(6)を両方の線分に描きましょう
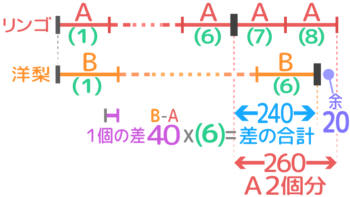
いつもは(N)の右端を比べますが、今回はリンゴと洋梨の(6)の右端同士を比べましょう
差の合計は240円で、これに余り20を加えた260円がA2つ分なので、リンゴは260÷2=130円と分かります。
「不揃いな差集め算」は以上です
つるかめ算を差集め算で解く
「つるかめ算」の解き方としては面積図をつかうものがよく知られています
(詳しく見たい人は「つるかめ算まとめ」を見て下さい)
しかし実は面積図よりも線分図で解く方が応用が利くのです。そして、この線分図は「差集め算」そのものなのです
基本のつるかめ
「100円のピザまんと80円の肉まんを合わせて20個買ったら1860円だった」場合
全部ピザまんだった場合の仮合計(2000)と実際の代金(1860)の合計の差140は、1個をピザまんから肉まんに買えた場合の差(100-80=20)がN個集まった(つまり肉まんをN個買った)もの、と考える。
80円の肉まんを
合わせて20個買ったら
1860円だった」
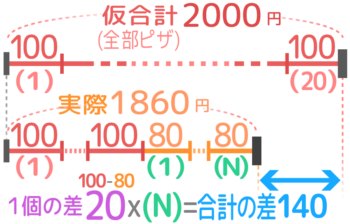
140÷20=7が肉まんの個数
関連記事「つるかめ算を面積図でないやり方で解く」も見て下さい。
マイナスがある場合(弁償算)
「皿洗いの仕事で洗うと賃金・割ると罰金」や「クイズに正解すると得点・不正解だと失点」などの場合。
例えば、「クイズに正解すると100円もらえるが、不正解だと30円の罰金になる20問のクイズで1350円もらえた場合、何問正解したか?」という問題
差集め算の基本パターンで、公式Bを使って
「全問正解の場合の仮合計」と「N問不正解の場合」の差の合計を1問を不正解になった場合の差(100+30=130:足し算になることに注意)で割ってNを出します

N=650÷130=5で、不正解は5問と分かります。
詳しくは関連記事「つるかめ算のまとめ」内の「弁償算の解き方」を見て下さい。
個数取り違え
「取り違え」とは、例えば、「アメ3個とガム5個」を買うつもりが、間違えて「アメ5個ガム3個」を買ってしまうことです。
個数を取り違えると、予定と実際で合計代金が当然変わりますが、ポイントは「取り違えても個数が共通する部分は変わらない」ことです。
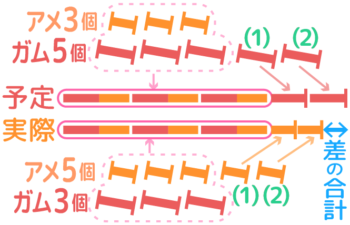
「アメ3個ガム3個」の個数共通部分は取り違えても変わらずに、個数が違う部分(2個分)で代金の差が生まれていますね
取り違え問題では、この「個数が違う部分」を差集め算にします
例題を解いてみましょう
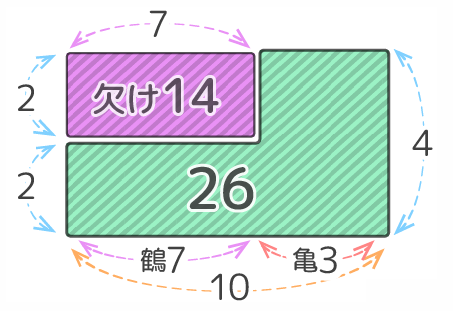
90円のピザまんと120円の肉まんを合計20個買うのに、ピザまんと肉まんの買う個数を予定と逆にしてしまったので、予定よりも180円高くなってしまった。 ピザまんと肉まんをそれぞれ何個ずつ買う予定だったか
線分図を書きます。個数が共通する部分はテキトーでも構いません(使わないことが多いので)
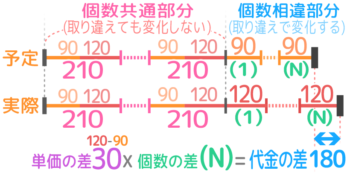
個数が違う部分では個数の差を(N)として差集め算の線分図を書くと、(N)=6と分かるので、ピザまんと肉まんの個数は和20,差6の和差算になる
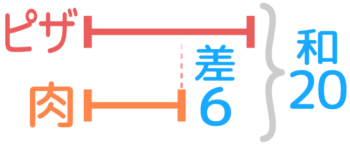
ピザまん13個、肉まん7個と分かります。
詳しくは関連記事「個数を取り違えたつるかめ算」を見て下さい。
次のステップへ
これで差集め算は大丈夫ですね?
差集め算が分かったら、いよいよ線分図の終着点「過不足算」へ進んで下さい!
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ