「算数の図が上手に書けない…」とお悩みの小学生と保護者の方へ。この記事では線分図の基礎の基礎である「線分の二等分」さらに「四等分」「八等分」の方法を図解します。小学校低学年のお子さんに「長さ」「量」の感覚を身につけてもらうのにはモチロン、分数の学習にも役立ちます。
保護者の方も紙と鉛筆を用意して、気楽に、お子さんと一緒にチャレンジしてみてはいかがでしょうか?もしかしたらお子さんが何が苦手なのか、教え方のヒントが得られるかもしれませんよ!
はじめに
 爽茶
爽茶「文章問題を得意にするには線分図を書くと良い」よく耳にすると思います。
しかし、線分図の「書き方」を教えてくれる先生は少ないのではないでしょうか?
そこで、当ブログではまず、線分図そのものに絞って書き方を練習していきます
なぜ等分しないといけないの?
では、どうして「等分」を練習するのでしょうか?それは「等分」が図を上手を書く一番のコツだからです。
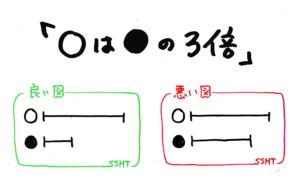
上手な線分図とは数量の関係が見た目の長さにも反映されているものです。例えば「◯は●の3倍」と書いてあったら見た目もそうなってないといけません。
この時、小さい方(●)を先に書いて、その3つ分を◯にするのが簡単です。
しかし、他の事との関連で◯を先に書く場合もあります。そのような時は◯を三等分しなくては行けません。線分を上手に三等分できないと上手な絵を書くことができませんね?
「等分」が上手な絵を書くコツだと思えてきませんか?思って下さい(汗)
では、はじめましょう!
二等分
最初は、二等分です。半分にすることですね。
「二等分なんて簡単に出来る!」
と、どの生徒も言いますw確かに線分の真ん中辺りに印を付けるだけです。
ところが!上手に出来ない生徒が多いです。そこで、まずコツを2つ説明します。
図を上手く書くコツ
アタリをつける
図がうまく書けない一番の原因は、いきなり濃く強く書こうとするから
絵を書くときは、必ず「アタリ」をつけます。
「アタリ」とは薄く書くことで、なれてくると頭の中で「アタリ」をイメージできるので、端から見るとスラスラ書いているようにみえます。
正しい姿勢で書く
二番目に、姿勢も大切です。スポーツと同じ!
ダメな例。その1

戦闘中じゃないんだから…
顔を紙に近づけすぎ!
図全体を視界に入れないと正確に判断できません
ダメな例。その2
右手で線分が隠れている。これでは正確に測れません
正しいやり方

余裕がありますね
顔を十分に紙から離して線分全体を視界に入れ、鉛筆は軽く持ちます。
二等分の手順
4ステップです。
- 芯先で探る
- 弱くアタリをつける
- よく観察する
- 強く区切る
①芯先で探る
まず、鉛筆の先を紙に「つけずに」線分の真ん中を探ります。
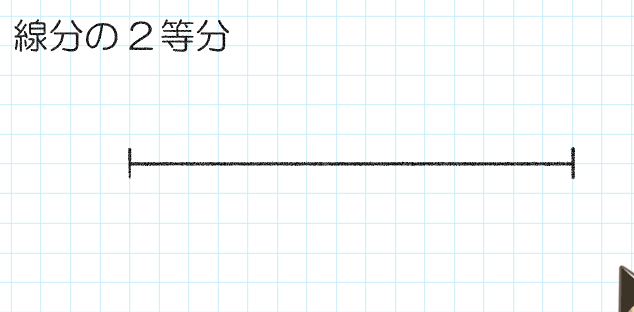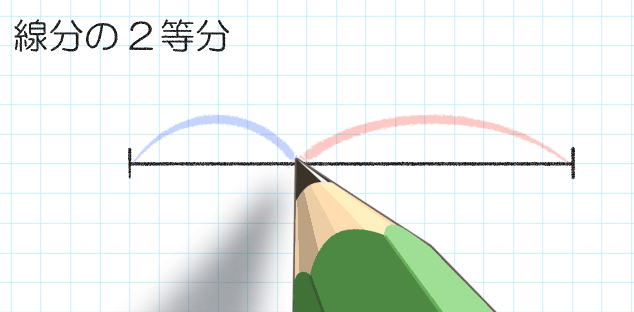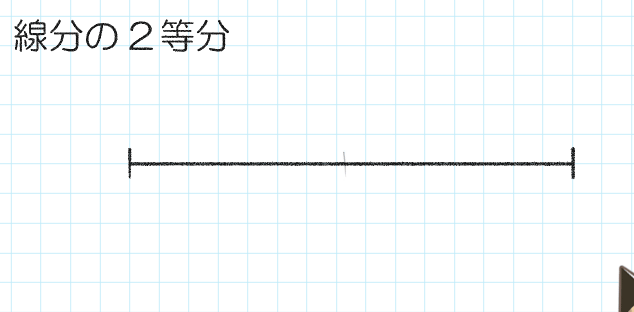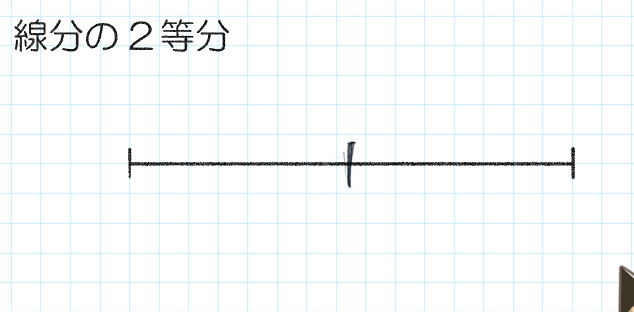
②弱くアタリをつける
真ん中と思えた辺りに薄く印(アタリ)をつけます。自分にしか見えないくらい薄~くです。
③バランスを見る
紙から目を話して、アタリが真ん中になっているかバランスを確かめます。
④濃く書く
今度は濃く、しっかりと「区切り目」を入れます。
アタリはあくまでも手がかりなので、このように、ずれてもOKです
では、最後に動画で見てみましょう
いかがでしたでしょうか?
最初はうまく書けなくて当たり前。何回か練習していればだんだん上手くなりますよ!
次は、二等分を利用して四等分を書いてみましょう。
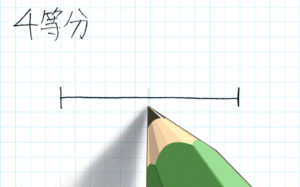
四等分
二等分の次は四等分です。
いきなり左から4つに分けようとしないで下さいね(^_^;)
4=2×2
二等分は「半分」でしたね。四等分は「半分の半分」です。
ですから、まず二等分して、それからまた二等分すればよいのです
(*^ー゚)b
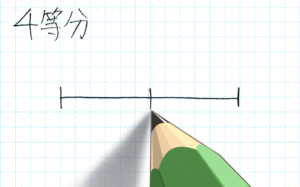
まず、2等分します。
探って弱くアタリ…眺めて濃く区切る
そして2つ出来た線分それぞれを2等分すると…
これで、四等分が出来ますね。
今見たように「4=2×2」というようにかけ算に分解できれば、どういう順番で切ればよいか分かるのです。この考え方はずっと使うので覚えておきましょう。
二等分・四等分と来たので、次は…カンのいい人なら分かるでしょうね
八等分
二等分、四等分の次は八等分です。
8をかけ算に直すと…8=2×4と直せますね。
が、さらに!
4=2×2なので、8=2×4=「2×2×2」 と直せます。
これで、どういう順番で切ればよいか分かりますね?
そうです。まず2等分して、さらにそれぞれを2等分して、またさらにそれぞれを2等分すれば良いとわかりますね!
では始めましょう。
まず、2等分します。イメージして、区切る
つぎに左右それぞれをさらに2等分
八等分が出来ました!

完成した八等分
さらに、16等分、32等分…とできますが、今回は、これで終了です。お疲れ様でした!
二等分のやり方が
理解できましたか?
 爽茶
爽茶今回の二等分シリーズは、全ての等分の基本ですので、何度も練習してみましょう。
次回は三等分のシリーズ「線分の三等分・九等分」です。
→線分図基礎の総合案内に戻る
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ