小学生】等差数列の応用問題！並行する数列(１)【中学受験

「ライバルに差をつけたい！」という中学受験生の方、お任せ下さい！東大卒講師歴20年の図解講師「そうちゃ」が数列の応用問題を分かりやすく教えます♪難関中学の入試問題にも刃が立つようになるでしょう！

等差数列の基本公式(復習)

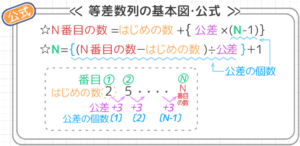
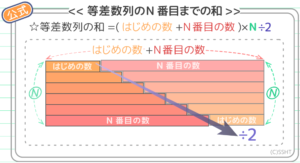
過去の記事の要点です。最低限、これらを頭に入れて下さい。

基本公式1と2

和の公式

では早速はじめましょう！

隠れた並行数列
(強い暗示)

例題1

この数列「1,3,4,5,7,7,10,9」は等差数列ではありません。

そこで、前回学習した階差数列を作ってみると…階差は 2,1,1,2,0,3,-1!!!
もうメチャクチャですね
(+_+)
では、どうしたらよいのでしょうか？！

小問1

表を埋めると…表を埋めると、こうなりますね

この表を落ち着いて観察すれば、
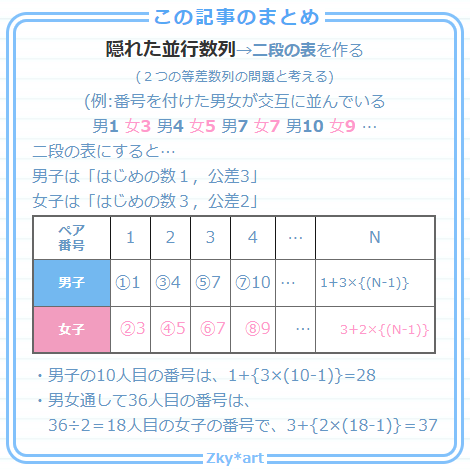
男子は 「はじめの数１，公差3の等差数列」
女子は 「はじめの数３，公差2の等差数列」
と分かります。

さて、このように数列の規則性が分かれば、あとは基本公式や和の公式を駆使して答えを出すことが出来ますね！

では次の小問に進みましょう

小問2

前半は等差数列の問題だから簡単ですね

男子7人目の番号は 1,4,7,10… という等差数列の7番目なので
[su_spoiler title=”いくつですか？” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]

「はじめの数１、公差３の等差数列」の「７番目の数」ですから、公式：N番目の数=はじめの数+{公差×(N-1)} を使って
1+{3×(7-1)}=19 と分かります

[/su_spoiler]

↓
次に、小問の後半部分「男子七人目の全体の順番」を考えます。

男女合わせた順番を「通番(つうばん、通し番号)」と呼び、①②のように丸数字で表しましょう。
表を見ると気付きますが、男子は奇数、女子は偶数になります。

また、男子と女子を２人ずつ「ペア」と考えて「ペア」にも番号をつけます。
この「ペア」番号は、そのペアの男子と女子の男女別の順番と言っても同じです。

例えば、③と④の二人は2番ペアにいて、③は男子の２人目、④は女子の2人目です。

表にするとこういう感じです
①↘②↗③↘④…とジグザグに進むイメージ

この表を使えば、男子7人目が男女合わせたら何人目か分かりますね？

[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]

男子7人目は、7番ペアにいるので…

男女合わせてだと13人目と分かります。

答: 番号19,男女合わせて13人目

[/su_spoiler]

反対に、通番からペア番号を出す方法を考えてみましょう。表をよく見て下さい。

女子は分かりやすいですね。通番÷２すると、ちょうどペア番号になります。
例えば、上の表で通番⑥の女子は⑥÷2＝3で3番ペアで女子の3人目です。

男子の場合は、本人よりも同じペアの女子に注目します。同じペアにいる女子の通番つまり(自分の通番+1)÷２がペア番号になります。
例えば、上の表で通番⑤の男子は、(⑤+1)÷2＝3で3番ペアなので男子の3人目と分かります。

以上の関係を使って問題を解いていきます。

小問3

表を活用しましょう

まず、通番20番の生徒は男女どちらの何番目でしょうか？

[su_spoiler title=”答えを表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]

通番⑳は偶数なので女子ですね
そして、⑳÷2＝10より、ペア番号が10なので、１０人目の女子と分かります。

[/su_spoiler]

これで、胸につけている数字も分かりますね
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]

女子の10人目が胸につけている番号は、「はじめの数3、公差2の等差数列」の「10番目の数」なので
公式：N番目の数=はじめの数+{公差×(N-1)} を使って
3+{2×(10-1)}=21 と分かります

答: 21[/su_spoiler]

小問4

まず、「52」を付けているのが男女どちらか考えます。
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]

表を眺めると…女子の番号は奇数しかありませんが、男子には偶数の番号の生徒がいるのが分かります。よって「52」は男子とわかります。[/su_spoiler]
↓
あとは、「はじめの数１、公差３の等差数列」で「52」になるのは何番目か、等差数列の「N」を求める問題になります。

[su_spoiler title=”Nはいくつ？” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]

公式：N={(N番目の数-はじめの数)÷公差}+1 を使って、{(52-1)÷3}+1=18 と分かります。
つまり「52」は男子の18人目です。

[/su_spoiler]

あとは、男子18人目の通番がいくつか出せば良いですね

[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]

男子の18人目は女子の18人目と18番ペアを組んでおり、女子の18人目は通番が18✕２＝㊱です。
男子はその１つ前なので㉟、全体では35番目と分かります。

答: 18人目の男子で 通番35番目

[/su_spoiler]

隠れた並行数列の解き方は以上です。表を使って落ち着いて考えるのがポイントです。

類題で練習して下さい。

類題1

隠れた並行数列
(弱い暗示)

例題2

一見普通の数列ですが、大きな数と小さな数が交互に並んでいて
２つのルールが混ざっていることがうっすらと暗示されています。

まずは差と階差数列が等差になっていないのを確認したら、先ほどと同じように2段の表を作ってそれぞれのルールを確認しましょう。

小問1

前章の問題と違って男女の区別が無いので、奇数番(①③⑤…)を数列A、偶数番(②④⑥…)を数列Bとして、表を作ります。

[su_spoiler title=”表を埋めると？” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]

こうなりますね。

A: はじめの数10,公差2の等差数列
B: はじめの数1,公差3の等差数列
と分かりました。

ペア番号と通番の関係は前章と同じです。
数列Bは通番はペア番号×2。例えば第3ペアにいるBは3×2＝通番⑥
数列Aは同じペアにいる数列Bの通番-1です。例えば第3ペアにいるAは、同じ第3ペアにいるBが3×2＝通番⑥なので⑥-1＝通番⑤と計算します

[/su_spoiler]

小問2

まず、12番目の数はABどちらの何番目でしょうか
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]

12は偶数なので、⑫は数列Bです。そして12÷2＝6で、⑫は第6ペアにあるので数列Bの6番目と分かります。

[/su_spoiler]

あとは、?を出すだけですね[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]

等差数列の基本公式
N番目の数＝はじめの数+{公差×(N-1)}　に 初めの数=1、公差=3,N=6 を入れて、Bの6番目(⑫)＝1+{3×(6-1)}＝16 と分かります。

[/su_spoiler]

小問3

まず、21番目の数はABどちらの何番目か求めます
[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]

21は奇数なので、㉑は数列Aです。
同じペアにある㉒を基準に、22÷2＝11で、㉑は第11ペアにあり、数列Aの11番めと分かります。

[/su_spoiler]

これで答えは出ますね。
[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn orange”]

等差数列の基本公式
N番目の数＝はじめの数+{公差×(N-1)}　に、はじめの数＝10、公差＝2、N=11 を入れて
Aの11番目(㉑)＝10+{2×(11-1)}＝30 と分かります。

[/su_spoiler]

小問4

(ヒント)
問題の語句から、数列Aと数列B両方に「100」があるのだろうと予想はつきますね。

まず、数列Aの方が「100」になるのはペア番号で何番か、そして通番で何番かを出しましょう

[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]

N={(N番目の数-はじめの数)÷公差}+1 で求めると、{(100-10)÷2}+1＝46　です。

そして、同じ46番ペアの数列Bが46×2＝92なので、「100」はその一つ前の91と分かります

[/su_spoiler]

次に、数列Bが「100」になるのはペア番号で何番か、そして通番で何番かを出しましょう

[su_spoiler title=”答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]
N={(N番目の数-はじめの数)÷公差}+1 で求めると、{(100-1)÷3}+1＝34　です。
そして、第34ペアの数列Bは34×2＝68と分かります

以上より、68番目と91番目が答えと分かります。

[/su_spoiler]

小問5

(ヒント)
旅人算的に考えましょう

[su_spoiler title=”解答を表示” style=”fancy” icon=”chevron-circle” class=”std no-trn pale”]

はじめはAの方が9大きいですが、Aは2ずつBは3ずつ増えるのでBが1づつ追いついて行きます。
(9m先を歩く速さ2ｍ/秒のAを速さ3m/秒のBが追いかける旅人算と同じ)

差が0になるには(9-0)÷(3-2)=9番後なので、1+9=10ペア目がABが同じになります。

10ペアはBが10×2＝⑳でAは20-1=⑲です。(ちなみに、AもBも同じく28になります)

答: 19番目と20番目[/su_spoiler]

理解できたでしょうか？類題で練習しましょう

類題2

まとめ

二種類の数列が並んでいる平行数列は、二段の表をサッと書いて整理すると分かりやすい。

爽茶そうちゃ

平行数列には続き(2)もあります。「数列の総合案内」から見て下さい。

追記1(2018/8/26)

今回は初めて本格的に「表」を使った記事だったので、非常に手間取りました…
(^_^;)

追記2(2019/1/6)

私の中では、この記事は一番時間がかかる大変な記事。だから類題が2つとも手が回っていない…

ブログ更新時のリライトでも、丸数字を表現するCSSを改善(こういうのN)するのでまーた手間取りました。

歴史の点数を上げたい受験生と保護者の方へ

年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ

2023年度生徒さん募集

2023年度の生徒さんの募集を開始しました(対面授業の一次募集)

東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。

詳しくはコチラのページを御覧下さい

新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから

中学受験でお悩みの方へ

そうちゃ

いつもお子様のためにがんばっていただき、本当にお疲れさまです

受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など

様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。

自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…

そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。

最後まで読んでいただきありがとうございました♪
この記事があなたの役に立てたなら嬉しいです!