「等差数列がよく分からない…苦手」という中学受験生の方、もしかしたら多くの事を覚えようとし過ぎなのかもしれませんよ。
実は、たった3~4個の公式で数列の半分以上の問題は解けてしまうのです。だから、その3~4個の公式と使い方をしっかり覚えるのが大切です。
この記事では東大卒講師歴20年の図解講師「そうちゃ」が数列の最重要項目と公式・その使い方を分かりやすく説明します。
記事を読みながら練習問題を解いていけば数列が苦手ではなくなるのは間違いなし!もしかしたら得意になっているかもしれませんよ!
目次の好きな箇所をクリックするとジャンプできます。
「Nを求める」の確認問題の答えが誤っておりました(S様がメールでご指摘下さいました。有難うございました。)。混乱なさった方に心よりお詫び申し上げます。
数列入門(~小3)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
はじめに低学年の生徒さん向けに、数列を得意にする準備です低学年のうちに数字を並べて書くことに慣れておくと、きっと数列が得意になりますよ!!
倍数を書いてみる
まず、かけ算の九九を延長して倍数の列を書いてみると良いでしょう。
3, 6, 9,12,15,18,21,24,27,30
33,36,39,42,45,48,51,54,57,60
……
10個並べたら改行する。
はじめの20個を書きながら縦・横のリズムをつかみます。(横に3ずつ・縦に30ずつ増えているのが分かります)
途中の省略を覚えて、100番目・200番目も書けるようになったらOKです。
書き方の例は参考記事「数列入門」を見て下さい。
等差数列を書いてみる
はじめの数を決めて、それに同じ数を足していきます。
3ずつ増えていく数列
5, 8,11,14,17,20,23,26,29,32
35,38,41,44,47,50,53,56,59,62
……
10個並べたら改行する。
これもはじめの20個を書きながら縦・横のリズムをつかんだら途中の省略を覚えて、100番目・200番目も書けるようになったらOKです。
等差数列の基本(受験小4)
中学受験を始めた小4のお子さんが対象ですが、小さい整数を使えば小3からの受験準備にも使えますよ♪
等差数列の意味
等差数列は等しい差で増えていく(減っていく)数字の列です。
=「はじめの数」から「等しい差(公差)」で増えていく
数字の並び
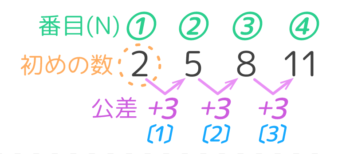
数列を見たら「差」と「番目」を書いて等差数列か見分けます。
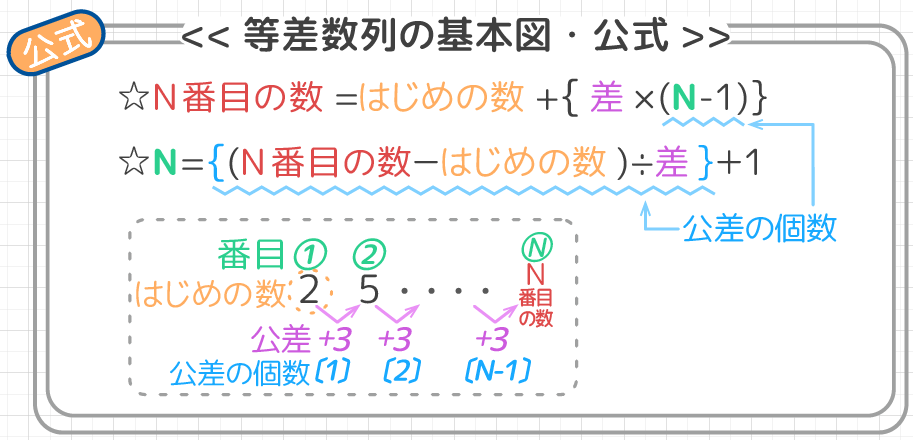
上の図を見ると、等差数列には4つの要素があるのが分かります。
①「はじめの数」…上の図の「2」
②「公差」…等しく増えていく数。上の図の「3」
③「N」(「番目」)…上の図の丸数字
④「N番目の数」…「2」「5」「8」と並んでいる数字そのもの
等差数列の基本問題は、この4つのどれかを聞かれるクイズだと思えばよいでしょう。
「等差数列」以外の数列
受験算数で一番よく出てくる数列は等差数列(単純な倍数を含む)なので、数列を見たらまず「差」を書き込んで等差数列でないか考えましょう
もちろん等差以外の規則を持った数列もあります。「階差数列」についてはコチラで、それ以外はコチラで説明しています。
「N番目の数」を求める
「はじめの数」と「公差」が分かれば「N番目の数」が自由に求められます。
この公式は絶対に覚えましょう!
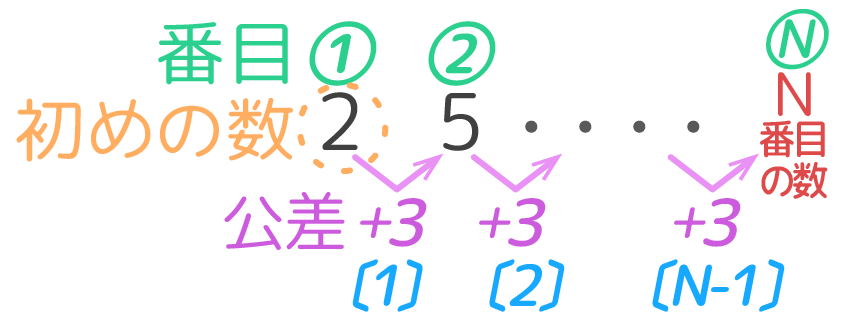
★N番目の数=初めの数+{公差×(N-1)}
(例)10番目の数=2+{3×(10-1)}=29
「公差」が「数字の個数=N」より1つ少ないことに注意します。
例えば3番目の数(N=3)は「はじめの数」に「公差」を3-2=2回プラスしたものです。
等差数列「1,4,7…」の8番目の数は?
→はじめの数+{公差×(N-1)}=( 1+{3×(8-1)}=22 )
等差数列「4,9,14…」の21番目の数は?
→はじめの数+{公差×(N-1)}=( 4+{5×(21-1)}=104 )
詳しい説明や応用問題が解きたい人は「等差数列とは?N番目の数の出し方」を見て下さい。
なお、この記事の一番下でプリントをダウンロードできます。
Nを求める
上とは反対に、ある数字が数列の何番目か=Nを求めることもできます。
ある数が数列のN番目の数である時
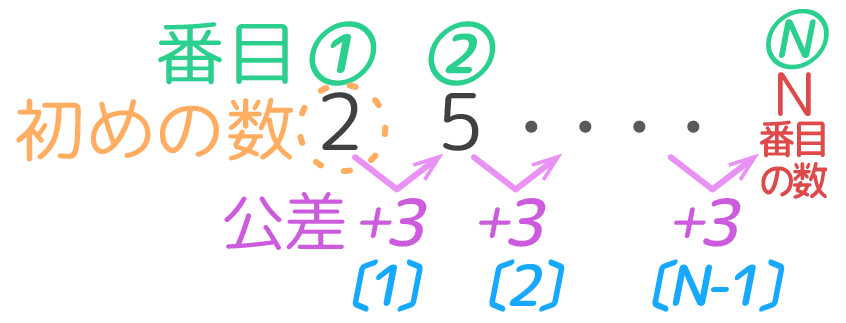
●数列での番目(N)
={N番目の数–はじめの数)÷公差}+1
==↑{…}は公差の回数を表す↑
(例)数列2,5,8…の32は何番目か?
→{(32–2)÷3}+1=11番目
「数字の個数=何番目か=N」は「公差」よりも1つ多いことに気をつけます。例えば「はじめの数」に「公差」を2回足した数は3番目の数です(N=3)。
この公式は、算数が得意な人は覚えなくても大丈夫です。苦手な人は覚えましょう。
80は数列「2,5,8…」の何番目ですか?
→公差の回数=(N番目の数–はじめの数)÷公差
=( (80–2)÷3=26 )回
→80は( 26+1=27 )番目
389は数列「11,20,29…」の何番目ですか?
→公差の回数は( {(389–11)÷9}=42 )回
→389は( 42+1=43 )番目
詳しい説明が読みたい・応用問題を解きたい人は「等差数列上の位置(N)を求めるには?」を見て下さい。
この記事の一番下でプリントをダウンロードできます。
公差を求める
数列の途中が抜けていても、数字が2個書いてあれば公差を求めることができます♪
=(N番目の数-はじめの数)÷(Nー1)
*(Nー1)が公差の回数になっています。
(例)等差数列「4,◯,◯,◯,32…」の公差?
→5番目の数が32,はじめの数なので、(32-4)÷(5-1)=7
公式自体を暗記しなくても問題が解ければOKです!
詳しい説明が読みたい人は「数列の初項・公差を求めるには?」を見て下さい
この記事の一番下でプリントをダウンロードできます。
初めの数を求める
はじめの数が分からない場合も、求めることができれば基本はカンペキです。
=N番目の数-{公差×(Nー1)}
*(Nー1)が公差の個数になっている
(例)等差数列「○,○,26,○,42」の「はじめの数」は?
→公差は(42-26)÷2=8
→はじめの数は26-{8×(3-1)}=10
公式を覚えずとも問題が解ければOKです。
詳しい説明が見たい人は「」を見て下さい。「数列の初項・公差を求めるには?」
なお、この記事の一番下でプリントをダウンロードできます。
数列の和(受験小4)
等差数列の「はじめの数」から「N番目の数」までの合計(和)を次の公式で求めることができます。
この公式は絶対に覚えてください。
等差数列の和=(はじめの数+N番目の数)×N÷2
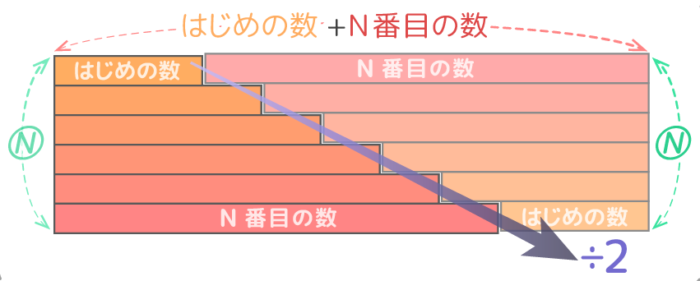
(問題を解く手順)
- はじめの数、公差、N(合計を求める個数)を確認
- N番目の数を はじめの数+{公差×(N-1)} で求める
- 数列の和を (はじめの数+N番目の数)×N÷2 で求める
確認テストをどうぞ
等差数列「5,16,27…」のはじめの数から14番目の数までの和は?
→14番目の数は( 5+{11×(14-1)}=148 )
→合計は( (5+148)×14÷2=1071 )
2,9,16,23,30…という数列がある。50番目までの数の合計は?
→50番目の数を求めると( 2+7×(50-1)=345 )
→50番目までの合計は( (2+345)×50÷2=347×25=8675 )
はじめから520までの数を足すといくつになるか?
→520の番目(N)を求めると( (520–2)÷7+1=75番目 )
→520までの合計を求めると( (2+520)×75÷2=522÷2×75=261×75=19575 )
詳しい説明が見たい人、もっと問題を解きたい人は「等差数列の和の求め方は?」を見て下さい。
この記事の一番下でプリントをダウンロードできます。
この後は、等差数列を利用した数列を見ていきます
階差数列の利用(受験小5)
4,5,7,10,14,19…
のように、差を並べてみると等差数列になっているような数列は公式が使えます。
(差を並べてできる数列が「階差数列」です)
この公式は覚えましょう!
差が等差数列(B)になる数列AのN番目
=Aのはじめの数+Bの(N-1)番目までの和
(例:A④=A①(1)+B①~B③の和(1+4+7=12)=13
*B④ではなくB③までなのがポイント!
確認テストをどうぞ
「6,7,9,12,16」という数列の13番目はいくつか?
→(もとの数列(A)の差を並べると「1,2,3,4…」という等差数列(B)になっている。Aの13番目=Aのはじめ+(Bの1番目から12番目までの和)=6+(1+2+3+…+12)=6+(1+12)×12÷2=6+78=84 )
「5,8,13,20,29…」という数列の27番目はいくつか?
→(もとの数列(A)の差を並べると「3,5,7…」という等差数列(B)になっている。Aの27番目=Aのはじめ+(Bの1番目から26番目までの和)。Bの26番目は3+2×(26-1)=53なので、Aの27番目=5+(3+53)×26÷2=5+754=759 )
問題を解きたい人は関連記事「階差数列の利用」を見て下さい。
この記事の一番下でプリントをダウンロードできます。
並行数列(受験小5)
二種類の数列が並んだり混じったりしている問題です。
分数の数列
分数の分母と分子がそれぞれ二種類の数列になっています。
約分があるのに気をつけて表にして(イメージして)解きます。
問題を解きたい人は関連記事「分数数列」を見て下さい。
暗示的な並行数列
一見、並行していると分からない場合です。
表などにして考えます。
二種類の数列が混じって並んでいる場合
→それぞれの数列を二段の表に分けてペア番号で考える。
(例) (男)1 (女)3 (男)4 (女)5 (男)7 (女)7 (男)10 (女)9 …
と並んでいる場合の前から15番目は?
| ペア番号 | 1 | 2 | 3 | … | N | |||
|---|---|---|---|---|---|---|---|---|
| 男子 | ①1 | ③4 | ⑤7 | … | 前から(N×2-1)番目 | |||
| 女子 | ②3 | ④5 | ⑥7 | … | 前から(N×2)番目 | |||
→男子は「はじめ1公差3」女子は「はじめ3公差2」の等差数列
→男子はペア番号×2-1(奇数)、女子はペア番号×2(偶数)
→前から15番目は15=8×2-1より8番ペアの男子で、
その番号は「はじめ1公差3」の等差数列の8番目
=1+3×(8-1)=22番
問題を解きたい人は関連記事「隠れた並行数列」を見て下さい。
群(グループ)数列(受験小5)
グループに分かれている数列です。何種類かに分類して考えます。
(クリックでジャンプ)
●等差数列を区切ったもの
(例1:均分) (2,4),(6,8),(10,12)…
(例2:均分) (2),(4,6),(8,10,12)…
●AかBの倍数
(例1)2か3の倍数を並べた数列
2,3,4,6,8,9,10,12,14…
(例2:2と3の倍数を除いた数列)
1,5,8,11,13,17…
●区切りごとに並びがリセットされるもの
(例1:整数)1/1,2/1,2,3/1,2,3,4/…
(例2:分数) 11,12,22,13,23,33,14,24,34,44…
等差数列を元にする連続型
等差数列をグループに分けたもので、周期算に出てきた三種類の番号(通番、周期番号、周期内番号)を意識すると簡単になります。

これがラクに解くコツです。
周期算を復習したい人は参考記事「周期算の公式・解き方まとめ」を見てください。
等差等分型
等差数列を同じ個数に区切った、こういう数列です。
6-1-0:等差等分型の群数列
この数列は「2,4,6,8,10…」という等差数列(はじめの数=2、公差=2)を2個ずつに区切ったものです。
2,4,/6,8,/10,12/…
これに、周期算で使ったのと似た三種類の番号(通し番号、群番号、群内番号)をつけてみます。
これを眺めると、数列と周期番号に特別な関係が見つかります。
それは第Nグループの最後(2番め)がN×4になっていることです。
これを利用すると、例えば第100グループの最後(2番目)の数、通し番号では2×100=200番目は100×4=「400」と分かりますし
逆に「400」は100×4であることから100グループ目の最後の数で2×100=200番目とも分かります。
この性質を使って問題を解いていきましょう。
例題
(2,4),(6,8),(10,12)…という数列について以下の問いに答えなさい
Q.第 グループの最初の数は何か?
Q.第10グループの合計はいくつか?
→第10グループの最後(2番め)は40。
→第10グループは(38,40)なので合計は78
等差不等分型
等差数列を、不等分に区切ったタイプ
(例)
(2),(4,6),(8,10,12)…この数列も「始めの数2、差2の等差数列」を元にしているが、区切りが1個、2個、3個と増えている。
ここでも三種類の番号(通し番号、群番号、群内番号)をつけてみます
各群の最後の数に注目すると、ルールが分かります。各群には群番号と同じだけの数が入っているので、各群の最後の数の通し番号はそれまでの群番号の和になっています。
例えば第4群の最後の数「20」の通し番号は1+2+3+4=10番目になっています。
また、この数列ではどの数も自身の通し番号の2倍になっています。
例えば5番目の数は「10」、9番目の数は「18」になっています。
以上のルールを使うと、第N群の最後の数(グループ内N番目)は、もとの数列の(1+2+3+…+N)番目で、(1+2+3+…+N)×2になるのが分かります。
Q.第7グループの前から3番目の数はいくつか?
→第6グループの最後の数は(1+2+…+6)×2=42、そこから右に3つ進むと第7グループの3番目になる。
→ 42),(44,46,48…
Q.第10グループの合計はいくつか?
→第9グループの最後は(1+2+…+9)×2=90 なので第10グループの最初(左端)は、92。
→第10グループは10個の数が並び、初めの数92公差2の等差数列なのでグループ最後(右端)の数は92+2×(10-1)=110
→第10グループの合計は(92+110)×10÷2=1010
等差数列でない連続型
等差数列以外では、連続する整数から2つの数の倍数だけを並べたもの(A)や、反対に2つの数の倍数だけを除いたもの(B)がよく出題される。
倍数だけの並び
(例)2か3の倍数を並べた数列
2,3,4,6,8,9,10,12,14,15,16,18…
2と3の公倍数6までの4個の数を1周期と考えると、第N周期の最後がN×6になっている
2,3,4,6/8,9,10,12/14,15,16,18/…
この最後の数を基準にすると、各グループの4個の数は-4,-3,-2つまりN×6-4,N×6-3,N×6-2 で表されるのが分かる。一つ前のグループの「(N-1)×6」を使って、+2,+3,+4と考えても良い。

倍数を除いた並び
(例1:2と3の倍数を除いた数列)
1,5,8,11,13,17…
2と3の公倍数6までの2個の数を1群として、第N群の最後にN×6が隠れていると考える。
1,5,(6)/7,11,(12)/13,17,(18)…
この隠れた数を基準にすると各群の2数は-5,-1 つまりN×6-5,N×6-1 で表されるのが分かる。一つ前のグループの「隠れた(N-1)×6」を使って、+2,+5と考えても良い。

(例2:3と4の倍数を除いた数列)
1,2,5,7,10,11,13,14,17,19,22,23,…
3と4の公倍数12までの6個の数を1周期として、第N周期の最後にN×12が隠れていると考える。
1,2,5,7,10,11,(12)/13,14,17,19,22,23,(24)/…
すると各グループの数はN×12-11,N×12-10,N×12-7,N×12-5,N×12-2,N×12-2 で表されるのが分かる。一つ前のグループの「隠れた(N-1)×12」を使って、+1,+2,+3と考えても良い。
Q1.40番目の数はいくつか?
→この数列は3と4の最小公倍数12で割った余りが1,2,5,7,10,11になる6個の数の周期になり、第N番グループの数は12×(N-1)に+1,+2,+5,+7,+10,+11 したものになっている。
→40番目の数は40÷6=6…4より第7グループの4番目なので、12×(7-1)+7=79
Q2.119は何番目の数か?
→119÷12=9…11 より、あるグループの最後と分かる。
→N番グループの最後とすると、12×(N-1)+11=119
なのでこの逆算を解いてN=10。第10グループの最後と分かった。
→119は6×10+0=60番目
断続型
グループの区切りごとに並びがリセットされるタイプ。
例1 1/1,2/1,2,3/1,2,3,4/… (実際は区切り線は無い)
通し番号、グループ番号、グループ内番号を整理しないと上手に解けない。
整数
(例1)一番単純なパターン
(例2)
2,2,4,2,4,6,2,4,6,8…
「2,4,6,8…」という「もとになる数の並び」が、1個、2個、3個と区切られるたびにリセットされている。
第Nグループの最初の数の「通し番号」は(1+2+3+…+(N-1))番で、最後の数の「通し番号」は(1+2+3+…+N)番。グループ内番号を「もとになる数の並び」で使えば数字が求められる。
Q1.17番目の数はいくつか。17番目のグループ番号をまず考えると、1+2+3+4+5=15より、通し番号15が第5グループの最後の数で、通し番号17は第6グループの2番目と分かる。各グループの2番目は全て4なので、通し番号17は「4」
Q2.第グループの合計はいくつか
Q3.17番目の数から27番目の数までの合計はいくつか
分数
分数の場合は、分母を基準に群を分けて、同様に考える。
11,12,22,13,23,33,14,24,34,44…
詳しくは関連記事「群数列」を見て下さい
その他の問題
差が等しくない,または差が等差になっていない数列
フィボナッチ数列
1,2,3,5,8,13…
①1+②2=➂3、②2+➂3=④5、のように2つの和で3つ目を決めていく数列。(→ウィキペディアの説明)
たまに入試で出ます。
見分け方
差を取ると1,1,2,3,5…と最初の1個以外はもとの数列と同じになっています。
4,7,11,18,…という数列の7番目を求めなさい
→( (差を取ると)3,4,7と最初の1個以外はもとの数列と同じなのでフィボナッチと分かる。2つの和で次の数字を順番に決めていくと、4,7,11,18,29,47,76で76と分かる)
等比数列
1,2,4,8,16,32…
①1×2=②4、②2×2=➂4、➂4×2=④8、のように次々に何倍かしていく数列
入試にはあまり?出ません。
カードのシャッフル
トランプ(カード)を「切る」(=英語でシャッフル)
(公式)
はじめの状態で一番上を除いたカードに上から順番(「差番」と呼びましょう)をつける
1回シャッフルすると、そのカードの「差番」が2倍される。差番が「カードの枚数-1」=「最大差番」を超えた場合は、「カードの枚数-1」で割った余りが「差番」になる。
例えば、10枚のカードがある場合、上から2枚目のカードの「差番」は①で、一番下(10枚目)のカードの差番は⑨(=最大差番)です。
1回シャッフルすると、上から2枚目にあったカードの「差番」は①→(x2)→②になるので、上から②+1=3枚目に位置します。
2回目のシャッフルでは、②→(x2)→④なので上から5枚目に、3回目のシャッフルでは、④→(x2)→⑧なので上から9枚目に位置します。
次の3回目のシャッフルでは⑧→(x2)→⑯で最大差番の⑨を超えるので、⑯÷⑨=1…⑦より差番は⑦になり、上から8枚目に位置します。
4回目のシャッフルでは⑦→(x2)→⑭,⑭÷⑨=1…⑤より差番は⑤、上から6枚目に位置します。
最初の位置に戻るのは、はじめの差番①をx2x2…した数を⑨で割って余りが①になるときです。書き出してみます。カッコ内が余りです。
①→②→④→⑧→⑯(7)→㉜(5)→64(1)
となって、6回目で元の位置に戻ると分かりました。
継子立て(ままこ だて)
円形に並べたものを1つおきに取り除いて行く遊び。(なんだそりゃw)
ちなみに「継子」というのは「ママの子供」ではありません(それはただの子供や…)。血がつながらない「義理の子」のことで、逆に血がつながらない義理の母は「継母」(ままはは:「ママのお母さん」ではありません。それは おばあちゃん や…)です。
童話では意地悪な継母にいじめられる女の子の話が出てきます。例えば、シンデレラをいじめていたのが「継母」です
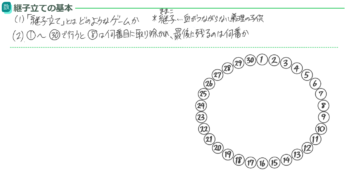
練習
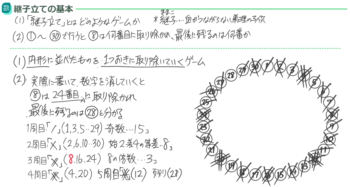
入試では書き出してみるのが結局一番安心できるので、書き出し(実際に消していく)の練習をどうぞ(クリックで拡大)
で、答えは下のようになります。
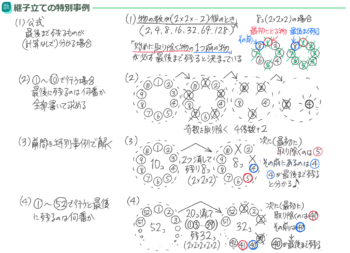
特殊事例(一発判明)
物の個数が「素因数分解すると2だけのかけ算になる数」例えば2,4,8,16,32,64…のときは最後に残るものが一発で分かります。
それを利用する方法(クリックで拡大)
物が100個くらいになると、この方法を使わないと無理でしょう。
ちなみに100個の場合は、36個(36個目の奇数は1+2×35=71)を取って残り64(2x2x2x2x2x2)個で特殊事例になり、次に取るのは73なので、その前の72が最後まで残る、と暗算で分かりますね♪
これだけ知っておけば「難関校にトップで合格したい人」以外は大丈夫でしょう。
プリントダウンロード
このサイトで使用した数列プリントの問題形式5枚と解答5枚あわせて10枚をまとめてダウンロードできます♪
zipファイルの中に問題だけのPDFと解答だけのPDFが入っているのでご利用下さい。
著作権は放棄しておりません。無断転載引用はご遠慮下さい。
ダウンロードにはパスワードが必要です。こちらから会員登録すると自動返信メールですぐパスワードを受け取れます。
*「パスワードを入れてもダウンロードできない」という方はブラウザや使用機種を変えて再度お試し下さい
これで数列のまとめは終了です
オススメ教材
 爽茶
爽茶●数列だけを解きたい場合、低学年の入門用には「等差数列(上)」
●数列だけでなく算数全体の復習をしたい場合、小4受験生には「算数の基本問題4年」(日能研)
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
保存セクション
す。
=「はじめの数」から「等しい差(公差)」で増えていく
数字の並び

数列を見たら

★N番目の数=初めの数+{公差×(N-1)}
(例)10番目の数=2+{3×(10-1)}=29
れれれ