中学受験を目指す小学5年生の方へ。数列の差が等しくないつまり等差数列でない場合は公式がつかえません。では、どうすればよいでしょうか?実はある条件を満たせば等差数列の公式を使うことができるのです!
東大卒講師歴20年の図解講師「そうちゃ」が送るこの記事を読めば、数列の「差」を並べた数列「階差数列」の使い方が分かってライバルに差をつけられますよ!
目次で好きな箇所をクリックするとジャンプできます。
(復習)等差数列の確認
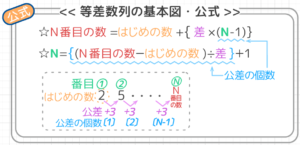
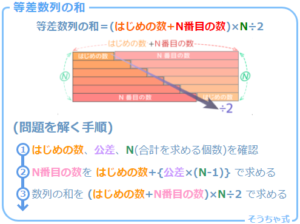
等差数列の基本をちょっとだけ確認。特に「等差数列の和」は絶対に思い出してください。
上の図を見ても「思い出せない…」人は「等差数列の基本とN番目の数の出し方」と「等差数列の和の公式と問題の解き方」を見て下さい。
差で作る数列(階差数列)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
今まで「数列を見たら等差数列と思え!」という勢いで問題を解いてきましたが、差が等しくない場合はどうしたらよいでしょうか。
階差数列を理解する
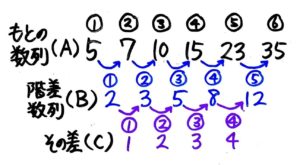
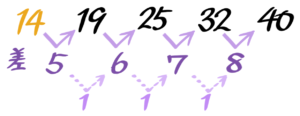
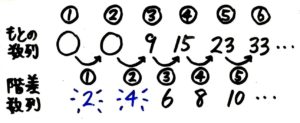
はじめの数(2)と2番目の数(3)の差は1ですが、2番目の数(3)と3番目の数(5)の差は2です。
差が等しくないので等差数列ではありません。
このように差を並べた数列を「階差数列」と呼びます。
→タイトルではもとの数列を階差数列のように書いていますが、
もとの数列の差を並べたものが階差数列です…
(^_^;)
階差数列を作る練習
少し練習してみましょう。「↓開く↓」にポインタをのせるか(パソコン)クリックすると(スマホ)、解答を見ることができます。
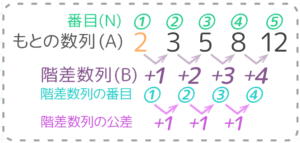
差を並べると2,4,6,8…となります。
これは「はじめの数が2、差が2の等差数列」になります。
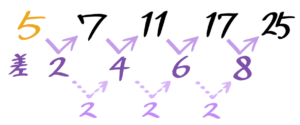
差を並べると5,6,7,8…となります。
これは「はじめの数が5、差が1の等差数列」になります。
階差数列が分かったと思うので、これを利用した問題を解いてみましょう。
階差数列の利用
ここからが本番です。階差数列を利用して問題を解いてみましょう♪
解き方を理解
Aのはじめの数「2」から4番目の数「8」までは6増加しています。
この増加分の6と階差数列Bの関係を考えると、
Bのはじめの数「1」2番めの数「2」3番目の数「3」の合計(和)です。
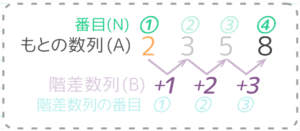
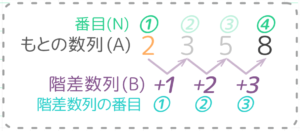
Bの4番目までの和ではなく、3番目までの和になることに注意です。植木算からずっと出てくる「木の数」と「間の数」の関係ですね
Aの10番目の数を求めなさい
先程の考え方を使うと、Aの10番目の数=Aのはじめの数+Bの9番目までの和 です。
➀まず「Aのはじめの数」は2です。
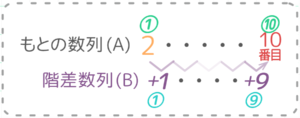
➁次に「Bの9番目までの和」を求めます。等差数列の和の公式 (はじめの数+N番目の数)✕N÷2 をB:1,2,3,4…にあてはめると、「はじめの数」=1,「9番目の数」=9「N」=9なので
「Bの9番目までの和」=(1+9)✕9÷2=45 になります。
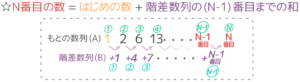
何度も言いますが、N番目の数を出すときは(N-1)です。
「80」はAの何番目か
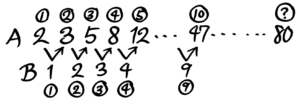

この続きの図を、Aに「80」が出てくるまで続ければ良いのです。
Aの12番は57+11=68、Aの13番は68+12=80(はい!出ました)。
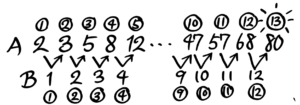
これで「80」はAの13番と分かりましたね。
計算間違いをしないように、図に書き込みながら解くことが重要です!
以上が階差数列を使った問題の解法です。
- ある数列(A)の差が等しくなくても…
- 差を並べた階差数列(B)が
等差数列になっていれば - もとの数列AのN番目の数を
階差数列Bを使って表現できる

- ある数のAでの位置(番目(N))
は地道に調べるしかない
分かりましたね。類題で練習して下さい。
練習問題で定着
類題2-1
(1)20番目の数を求めよ
(2)「396」は何番目の数か?
小問1
もとの数列(Aとします)の差を調べると等しくありませんが、とりあえず並べます。階差数列ができました(Bとします)。
Bは「2,5,8,11,14…」という数列で差を調べると全部3なので、はじめの数=2、公差=3の等差数列でした。
((図))
ここでさっきの公式を用いると、Aの20番目の数=Aのはじめの数+Bの19番目までの和 になります。
Bの19番目=はじめの数2+公差3✕(19-1)=56 で、Bの19番目までの和は、(Bのはじめ+Bの19番目)✕19÷2=(2+56)✕19÷2=551
これで答えが出ますね。Aの20番目の数=Aのはじめの数+Bの19番目までの和=4+の551=555 と分かります。
答: 555
小問2
番目=Nを出すので地道に調べますが、今まで分かった情報を元に「396」が、どの辺りにあるかを予想します。
設問で「44」が6番目、小問1で「555」が20番目と分かっているので、「396」は20番よりも前で、「555」から戻るように探すのが良いと分かります。
((図))
「555」の直前にあるBの19番を求めると、2+3×(19-1)=56と分かるので図を描きます。
((図))
計算した結果をこの図に書き込んでいきましょう。
Aの19番目は555-56=499
Aの18番目は499-53=446
Aの17番目は446-50=396 はい出ました!
「396」はAの17番目と分かりました。
答: 17番目
次は、少し変わった階差数列です
類題2-2
問題の数列(Aとします)の差を並べると、20,18,16,14,12 となります(階差数列=B)。Bの差は全て2で「減る」タイプの等差数列になっています。
減るタイプは公式が少し変わって「N番目の数=はじめー{差×(N-1)}」になることに気を付けましょう。
Aの10番目=Aのはじめの数+Bの9番目までの和 です。
Bの9番目=Bのはじめの数20-{Bの公差2✕(9-1)}=4、Bの9番目までの和=(Bはじめの数20+Bの9番目の数4)✕9÷2=108 と分かります。
これで、Aの10番目=Aのはじめの数+Bの9番目までの和=1+108=109と分かりました。
答: 109
次は少し応用です。
類題2-3
(1)はじめの数を求めよ
(2)15番目の数を求めよ
小問1
(ヒント)
問題の数列(A)が分かっている部分の差を調べて並べます
問題の数列(A)が分かっている部分「9,15,23,33」の差を並べる(階差数列を作る)と「 6,8,10」 という等差数列になっていました♪
きちんとAとBを並べて書くと、Bの3番=6、4番=8、5番=10と分かるので、そこから遡るようにBの2番=4、Bのはじめ=2 も分かります
次にAをさかのぼってAの2番は9-4=5,Aのはじめは5-2=3 と分かります。
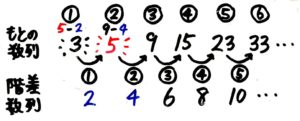
答: 3
小問2
(ヒント)
Aのはじめの数が分かったので、階差数列の公式が使えますね
Aの15番目=Aのはじめの数+Bの14番目までの和 です
↓
Bの14番=Bのはじめの数2+{Bの公差2✕(14-1)}=28、Bの14番目までの和= (Bのはじめの数2+Bの14番目の数28)✕14÷2=210 と分かります。
↓
これで、Aの15番目=Aのはじめの数3+Bの14番目までの和210=213とと分かりました。
答: 213
応用問題に挑戦
最後の類題は…応用です。
ひと目見れば等差数列ではないと分かります。
そこで階差数列を調べてみても、2,3,5,8,12…これも等差数列ではありません。
そこで、階差の差を調べると1,2,3,4… 見事に!等差数列になっていました。
つまり、この数列は「階差の階差が等差数列である数列」だったわけですね。
それでは10番目をどのように求めればよいでしょうか?
6番まで出ているので、10番までは少し頑張って図を完成させれば出せそうですね。
完成させると…
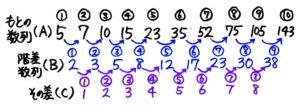
こうなって143と分かりました。
小学生は、このように書き出すのが良いと思います(高校生になれば、これも公式にできるのですが…)。
階差数列の問題は以上終了です!
まとめとプリント

この記事で使った問題の「解答解説」プリントをダウンロードできます。書き込み可能な「問題」プリントはコチラでまとめてダウンロードできます。
 爽茶
爽茶オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
(管理者用)保管セクション
す。
- ある数列(A)の差が等しくなくても…
- 差を並べた階差数列(B)が
等差数列になっていれば - もとの数列AのN番目の数を
階差数列Bを使って表現できる

- ある数のAでの位置(番目(N))
は地道に調べるしかない
分かりましたね。類題で練習
数列
「階差数列」の公式
差が等差数列(B)になる数列AのN番目
=Aのはじめの数+Bの(N-1)番目までの和

(例:A④=A①(1)+B①~B③の和(1+4+7=12)=13
*B④ではなくB③までなのがポイント!
平行数