「過不足算が難しい」図の書き方が分からない」という中学受験生の方へ
確かに「過不足算」は「人が座っていない長イスが2脚あり、5人がけなのに3人しか座っていない長椅子が1脚あって…」等の複雑な問題が出てきます
(>_<)
でも大丈夫!東大卒講師歴20年の図解講師「そうちゃ」が「過不足算」の基本から複雑な問題まで解けるような図の書き方を分かりやすく説明します。
記事を読んで図を真似しながら問題を解けば「過不足算」が苦手でなくなるのは間違いなし、得意になってしまうかもしれませんよ♪
四谷大塚「予習シリーズ」を使用している方は予シリを解説した「ヨリシス」シリーズを御覧ください
過不足算の準備
 爽茶
爽茶過不足算は差集め算の応用
過不足算は「差集め算」の2本の線分図にもう1本線分図が加わった応用です。差集め算が苦手・忘れた人は関連記事「差集め算」を見直すのをすすめます
余りと不足の表現
「余り」と「不足」を線分図にする練習です
二本の線分図の長短
「余り」「不足」は「配ろうとする計画で必要な個数」と「実際にある個数」の大小関係で、線分図にするとこんな感じ
「計画」と「実際」どちらの線分図が長いか(多いか)を考えると分かりやすいでしょう。
この考え方で線分図を書く練習をしてみましょう
練習問題
例1
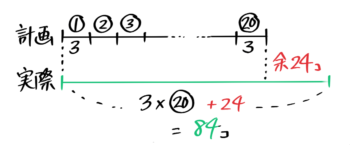
20人の生徒にアメを3個づつ配ろうとしたら24個余った。アメは実際に何個あるか?線分図を書いて解きなさい
余ったので「実際」が「計画」より長くなります。
まず、配ろうという「計画」の線分を3の長さの区切りがつながった形で書き、その下に24長い「実際」の線分を書く
これで「実際」のアメの個数は3×20+24=84個と分かります。
例2
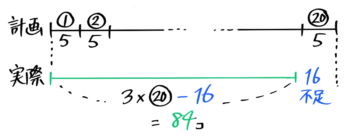
20人の生徒にアメを5個づつ配ろうとしたら16個足りなかった。アメは実際に何個あるか?線分図を書いて解きなさい
足りない場合は「計画」が「実際」より長くなります。
まず、配ろうという「計画」の線分を書き、その下に区切りの長さ(5)を基準にして16短い「実際」の線分を書く
そして「実際」の長さは20×5-16=84個です
確認テスト
面積図
面積図にすることもできます。
上と同じ「20人の生徒にアメを3個づつ配ろうとしたら24個余った」「20人の生徒にアメを5個づつ配ろうとしたら16個足りなかった」で示します


2つの図を重ねて書くので線分図よりも書くのが難しいですね。線分図が書ければ大丈夫です
準備は整ったので、いよいよ「過不足算」の問題に挑戦です
基本の過不足算
単純な「余り」と「不足」が書けたら、
「基本の過不足算」は決まった人数にアメを配ることを「計画」した時にアメが余ったり不足したりする問題です。
余ったり不足したり
一番目は、はじめの計画(計画A)だと余り、つぎの計画(計画B)で配る数を増やしたら足りない、という場合(一般に「過不足算」と言って連想されるのはこのタイプ)
1-1:余ったり不足したり
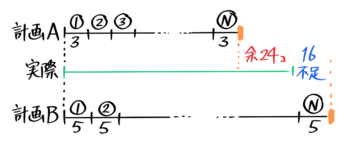
クラスの生徒にアメを3個づつ配ろうとしたら24個余ったので、5個づつ配ろうとしたら16個足りなかった。アメは実際に何個あるか?
線分図(差集め算)で解く
文章の順に「計画A」「実際」「計画B」三本の線分を書きます。長さの関係が「計画A」<「実際」で「実際」<「計画B」になるように書きます。
差の合計はa+bになる
さらに、AとBの差を四本目として書き込むと図が完成です。
これを頭に入れて、先程の例題を解いていきます。
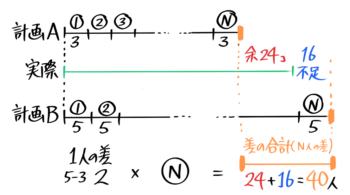
クラスの生徒にアメを3個づつ配ろうとしたら24個余ったので、5個づつ配ろうとしたら16個足りなかった。アメは実際に何個あるか?
生徒の人数が分からないのでNとして区切りを書きます。この時、Nの区切りの右端を濃く書いて下さい。
1人の差は2個、人数は?(N)、「差の合計」はNの区切りの右端の差で24+16=40個になります。
これで、差の合計(40)=1つの差(2)×人数(N=?) という関係が分かるので、N=40÷2=20人と求めます。
さらにアメの個数は3×20+24(Aを使った計算)または5×20-16(Bを使った計算)で84個と分かりました。
確認テスト
何人かの子どもたちにアメを6個ずつ配ると11個余り、8個ずつ配ると3個足りない。アメと子供の数を求めよ
面積図で解く(準備中)
基本の過不足算は面積図で解説するテキストもあるので、そのやり方も載せておきます
この基本の過不足算だけならば、面積図で解いても良いですが、線分図も書けるようにしておきましょう。
また余る
「はじめの計画(計画A)で余り、つぎの計画(計画B)で配る数を増やしたのにまた余る」場合です
さっきは「計画A」<「実際」<「計画B」という関係でしたが、今度は「実際」が「計画A」だけでなく「計画B」よりも多いので「計画A」<「計画B」<「実際」という関係になります。
b
差の合計はa-bになる
例2
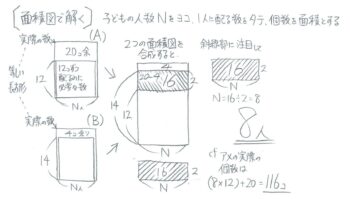
何人かの子供たちにアメを12個ずつ配ると20個余り、14個ずつ配ると4個余る。
1人の差は2個、人数は?(N)、「差の合計」はNの区切りの右端の差で20-4=16個になります。
これで、差の合計(16)=1つの差(2)×人数(N=?) という関係が分かるので、N=16÷2=8人と求めます。
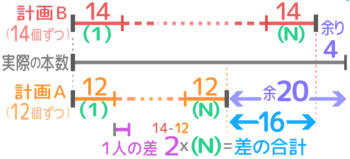
さらに実際のアメの個数は12×8+20(Aを使った計算)または14×8+4(Bを使った計算)で116個と分かります。
面積図の場合
こんな感じで解けますが、線分図で解けるほうが大事
また不足
「はじめは不足し配る数を減らしたのにまた不足」という場合です
今度は「実際」<「計画B」<「計画A」という関係になります。
差の合計はb-aになる
例
何人かの生徒にアメを8個ずつ配ろうとしたら33個足りなかったので6個ずつ配ろうとしたが、まだ1個足りなかった。アメは何個か?
1人の差は2個、人数は?(N)、「差の合計」はNの区切りの右端の差で33-1=32個になります。
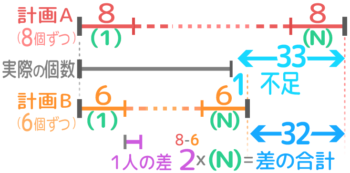
差の合計(32)=1つの差(2)×人数(N=?)なのでN=32÷2=16人です。
さらにアメの個数は8×16-33(Aを使った計算)または66×16-1(Bを使った計算)で95個と分かります
確認テスト(作成準備中)
小まとめ
これまで出てきた3つの場合を並べるとこうなります。
●余ったり不足したり
はじめの配り方(A)ではモノが余るので
1人あたりの個数を増やして配ったら(B)モノが足りなくなった
または
はじめの配り方(A)ではモノが足りないので
個数を減らして配ったら(B)モノが余った
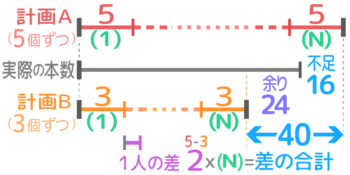
●また余る
はじめの配り方(A)ではモノが余るので
個数を増やして配ったが(B)まだ余っている

●また不足
はじめの配り方(A)ではモノが足りないので
少なく配ったが(B)まだ足りない

不ぞろいの過不足算
配る人数が予定よりも増えたり減ったり、つまり予定と実際の「N」が揃っていない問題。
Nを求めるタイプと単価を求めるタイプがある
Nを求める
(例題)
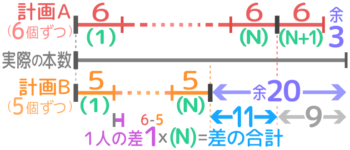
何人かの生徒にチョコを6個ずつ配ると3個余るはずだったが、当日1人が欠席し配るのも5個づつに減らしたので20個余った。チョコは何個あるか?
当日の人数を「N人」、計画時の人数は「N+1」と書き、その前の区切りには「N」と書きます
★このように線分図に(N)を2つ書くのが最大のコツです
Nが2つあれば、基本の過不足算と同じように、(N)の右端を見比べて差の合計を20-(3+6)=11個と求めて、1人の差が1個なので、当日の人数(N)=11÷1=11人と求められます。
そして、チョコは5×11+20=75個(計画Bを使った場合)または6×12+3=75個(計画Aを使った場合)と分かりますね。
練習問題
買い物に行ったAさんは1本150円のジュースを何本か買って100円余る予定だったが、1本が120円になっていたので予定よりも2本多く変えて40円余った。はじめに何円持っていたか
予定の線分は150円の区切りをN個つなげて所持金より100円少なく、実際の線分は120円の区切りを(N+2)個つなげて所持金より40円少ない
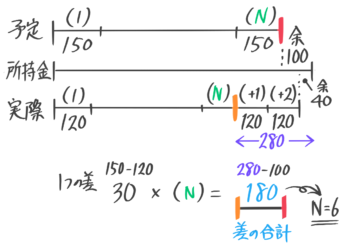
(N)の右端同士を比べると差の合計は180円,1個の差は30円なので、N=180÷30=6個。
所持金は150×6+100(予定から)または120×8+40(実際から)=1000円と分かります。
単価を求める
例題
Aさんが持っているお金でサインペンを買うと8本買えて80円あまり、ボールペンを買うと13本買えて30円あまる。サインペン1本がボールペンより50円高い。(1)サインペンとボールペンはそれぞれいくらか
(2)Aさんの所持金はいくらか
問題文を線分図にして、8本の区切りの右端を比べると差の合計=50×8=400円、ボールペン5本分=450円と分かる
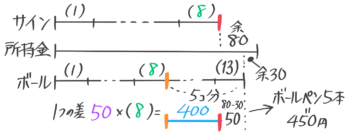
ボールペン1本=450÷5=90円、サインペン=90+50=140円
所持金は90×13+30=1200円と分かります
端数の過不足算
現実世界で何かを配ってみると、予定通りにもらえない人や、全くもらえない人が出てくることがありますよね?これが「端数の過不足算(Nがそろっているが端数がある)」です。
この「端数」のせいで面積図にするのが難しくなるので、線分図で解きましょう。
準備(端数の表現)
端数を線分図にする練習をしてみましょう
例1
生徒にアメを6個づつ配ったところ、1人の生徒は4個しかもらえず、まったくもらえない生徒も1人いた。アメは何個足りないのか
「計画」の線分図は6個づつ配ったように書きますが、「実際」の線分図は「計画」の最後から2人目の途中まで(4人)の長さになる。

不足しているのは、最後から2人目のあと2個と最後の1人の6個を合わせた8個と分かります。
次に長イスの問題で端数を表す練習です
例2
子供たちを長イスに7人ずつ座らせたところ、1人しか座らないイスが1つと誰も座らないイスが2つできた。あと何人座れるか
「計画(7人ずつ座らせたときに全部で座れる人数)」の線分を基準に「実際の人数」の線分の長さを考えると、「計画」の最後から3脚目の途中まで(1人)の長さになる。
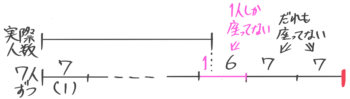
あと座れるのは、最後から3脚目のあと6人と最後の2脚の7×2=14人を合わせた20人と分かりますね
「半端」の表し方が分かったので、この書き方で問題を解いてみましょう
余って足りない
例
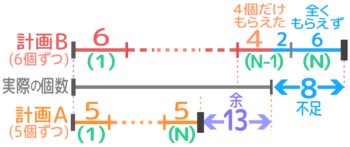
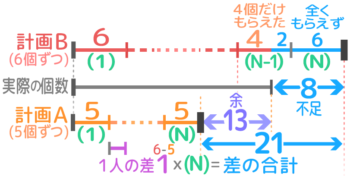
何人かの生徒にアメを5個ずつ配ったところ13個余ったので、今度は6個ずつ配り直したところ1人の生徒は4個しかもらえず、まったくもらえない生徒も1人いた。アメは何個あったか
計画Aでは13個余り、
計画Bでは「4個しかもらえない生徒」と「全くもらえない生徒」の分が2+6=8個足りない
これをに線分図を書くとこうなります。
2つの(N)の右端を比べると…差の合計は21と分かります。
1人の差は6-5=1個なので、人数(N)=21÷1=21人。
アメの個数は6×21-8=118個
例2
子供たちを長イスに5人ずつ座らせたところ、4人座れなかったので、今度は7人ずつ座らせたところ、1人しか座らないイスが1つと誰も座らないイスが2つできた。子供の人数とイスの数を求めよ
子供の人数を真ん中にして、計画AとBの線分図を上下に書く
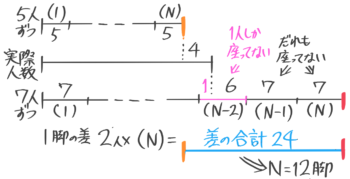
計画AとBの(N)の区切りの右端の間=差の合計は5人ずつのときの余り4+7人ずつのときのあと座れる人数6+7+7=20人の合計24人なので、1脚の差(2)x(N)=24よりN=12脚
子供の人数=5×12+4=64人と分かります
まだモノが足りない/席が余る
例題
生徒たちを長イスに12人ずつ座らせたところ、誰も座っていないイスが1つと8人しか座っていないイスができた。そこで10人ずつ座らせたところ、最後のイスには8人しか座らなかった。生徒の人数とイスの数を求めよ
はじめに(N)脚に12人がけで座れる人数の線分図を書くと、実際の人数の線分は最後から2番目のイスの8人までの長さになる。そして10人がけで座れる人数は最後のイスの8人まで

1脚に座る人数の差は2人、(N)の右端の区切りの間の長さは4+12-2=14人なので、N=14÷2=7脚、生徒の人数は10×7-2=68人
半端で不揃いの過不足算
いよいよ面倒くさくなってきました(汗)
ペアを作る過不足算
けっこうな応用です。
二種類の量を別々の線分図に書いていたのを
二種類の量ひとつづつをセットにして、一本の線分にする
例えばクラスの男女それぞれに違う量を与える場合
人数の差が分かっている場合
例題
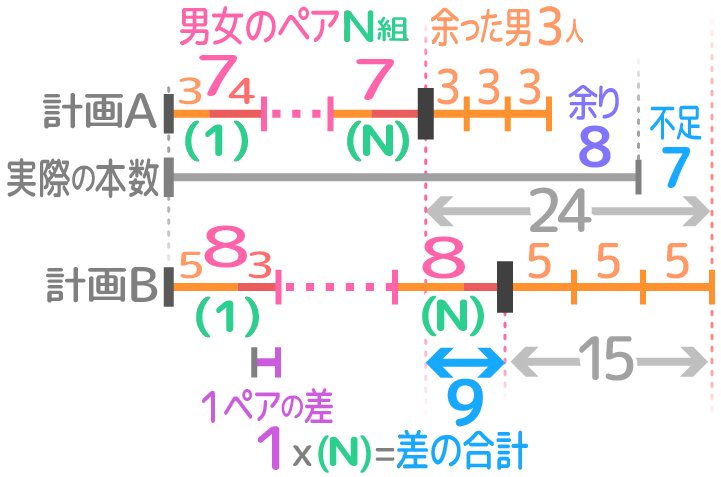
男子が女子より3人多い。男子に3個、女子に4個ずつアメをあげると8個余る。一方、男子に5個、女子に3個ずつあげると7個足りない。
男子と女子をペアにする(N組できたとする)。3人の男子はペアになれない。
最初の計画では1ペアに7個ずつ、3人の男子には計9個のアメを配って8個余る
二番目の計画では1ペアに8個ずつ、3人の男子には計15個のアメを配って7個足りない
アメの個数を真ん中に三段の線分図を書き、ペアの個数(N)の右端を比べる
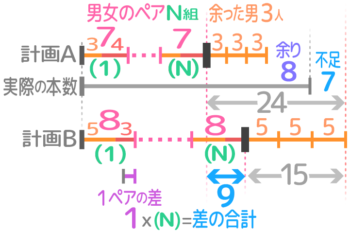
差の合計は9になり、一つの差は1なので、N=9÷1=9で、ペアは9組(女子の人数と同じ)で、男子は9+3=12人になる。
合計が分かっている場合
男女差が分からず男女の合計が分かっている場合は、二種類の事例での男女の配布量の合計が等しくなっている
例題
男女の合計が18人。男子に4個、女子に4個ずつアメをあげると7個余る。一方、男子に3個、女子に5個ずつあげると5個余る。
問題文から、女子に増やした計画の方が必要なアメの個数が多くなるので女子の人数が多いと予想できる(N人多いとしておく)。
ペアをつなげると、どちらの計画でも1ペアのアメは8っ子なので、ペアの部分は長さが同じになる。
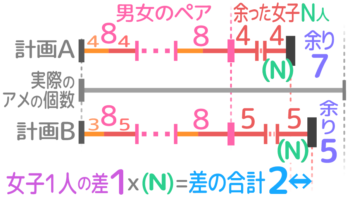
余った女子N人の部分で差の合計が2になり、1人の差が1なので、N=2÷1=2で余りの女子が2人、つまり女子が2人多いと分かる。
男女の和が18で差が2なので和差算の計算により、男子8人・女子10人と求められる。

オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■算数(割合、食塩水、売買、仕事/ニュートン算、時計算、すい体 etc)
★理科(月の満ち欠け、星の動き、電流、水溶液/気体の性質 etc)
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ