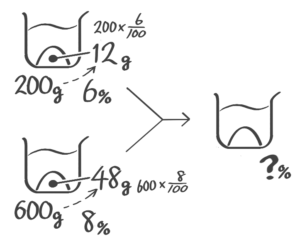
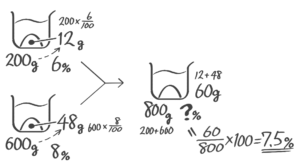
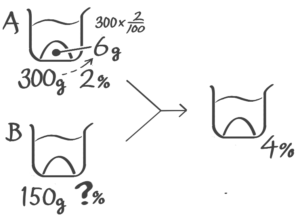
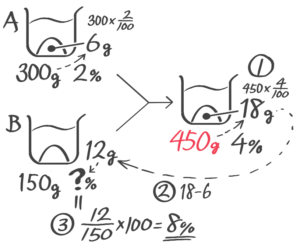
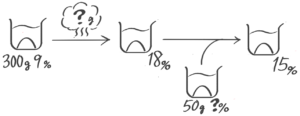
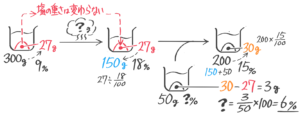
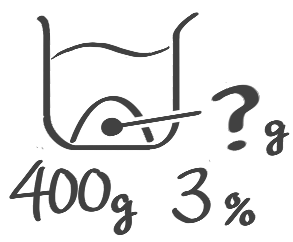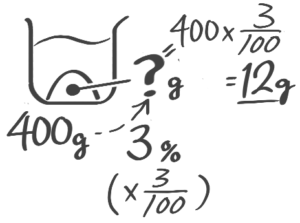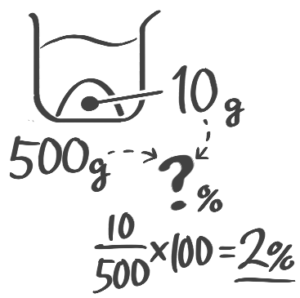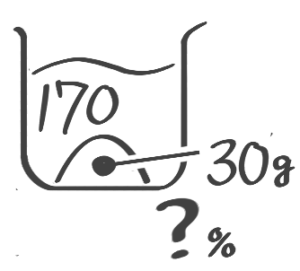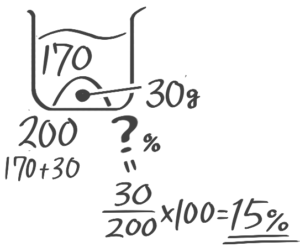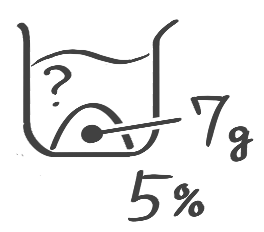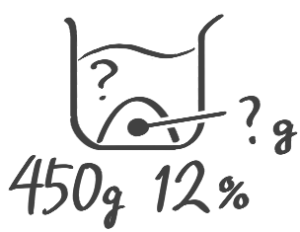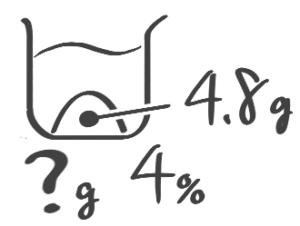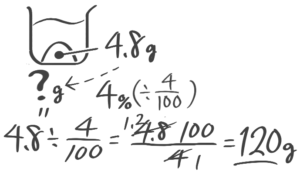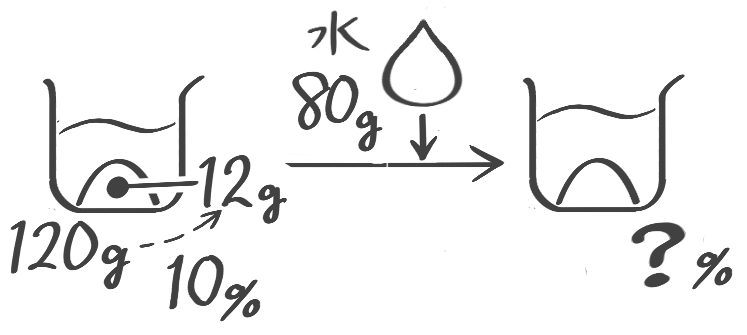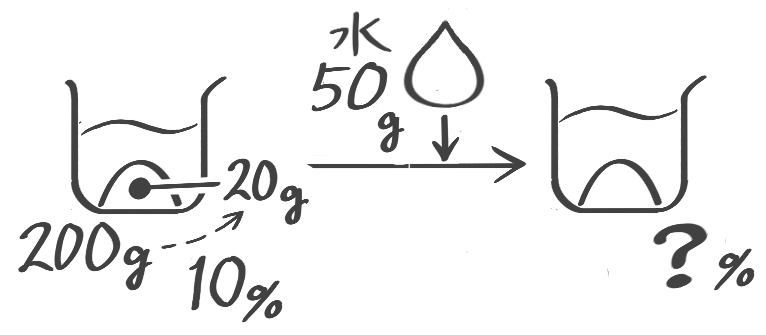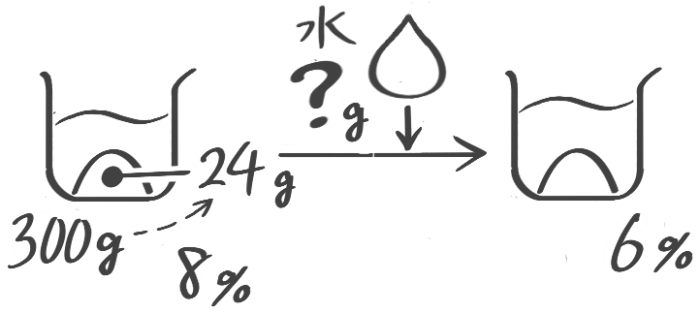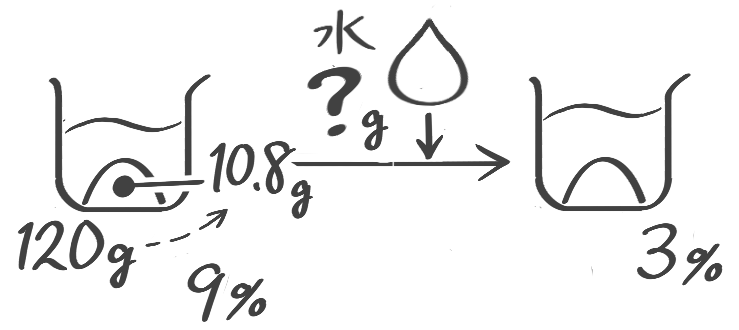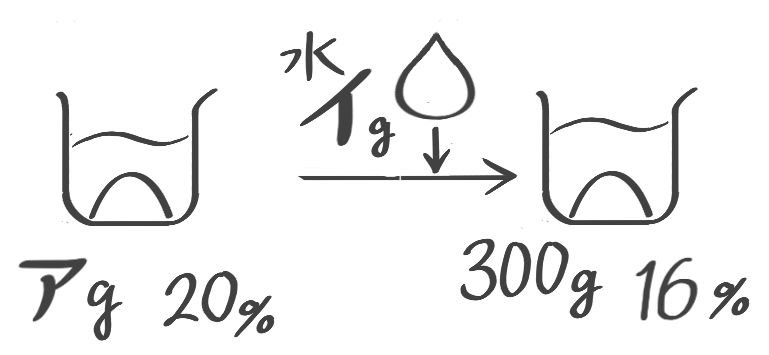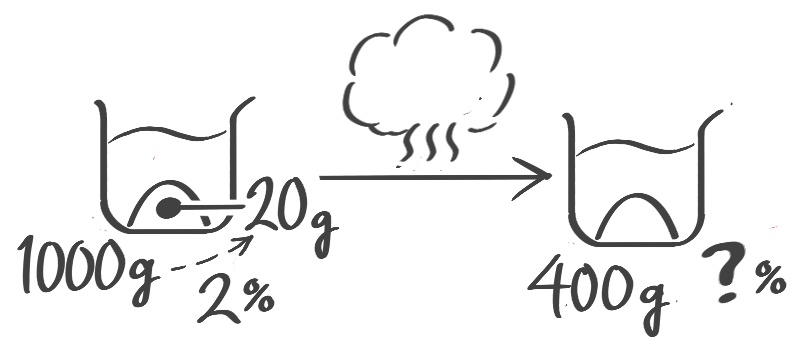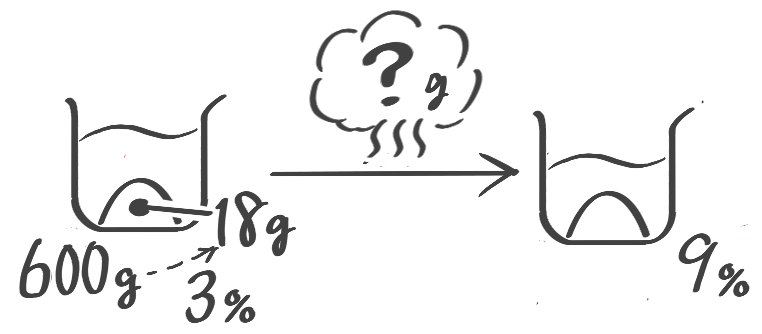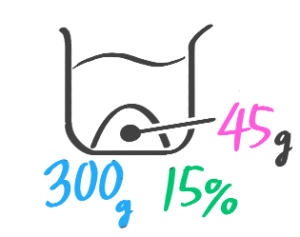「濃度の問題が苦手！」という中学受験生の方へ。確かに食塩水を作ったり混ぜたり…色んな問題・色んな計算があってややこしく感じられるかもしれません
でも、実は使う公式は3つ(1つ)だけ、問題の種類も基本は5種類くらいしかなく、そして食塩水の問題では、2つの図の書き方をマスターすれば大部分の問題に対応できます。
これらの公式・図の書き方をしっかり練習して、その使い方として問題を解けるようにすれば標準までは必ず解けるようになりますよ
この記事では東大卒講師歴20年以上の図解講師「そうちゃ」が濃度の基本公式や図の書き方から入試問題の解き方まで分かりやすく説明します
記事を読んで例題を解けば「濃度」の問題が得意になって、入試本番でも他の受験生に負けないでしょう♪
この記事は非常に長いです。目次をクリックして好きなところから読んでもいいでしょう。
濃度の基本
割合(復習)
濃度は割合の一分野で、図と公式は割合とほぼ同じです。
割合の図(矢印図)
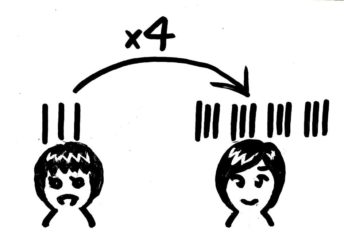
姉は妹の4倍持っている」
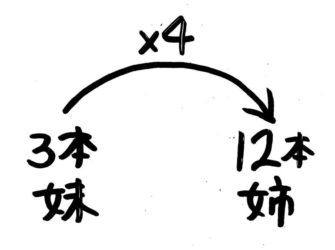
3×4=12を表す
図と三公式
矢印図
→3つの数が「A×B=C」の関係にある時に、
矢印の向きに沿って「A」「B」「C」を並べた図
(例)「2×3＝6」の矢印図
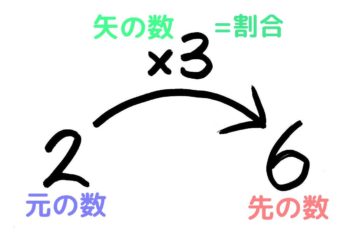
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
学校などで習う「割合の三公式」(中身は矢印図の公式と同じ)
➊割合＝くらべる量÷もとにする量
❷くらべる量＝もとにする量×割合
➌もとにする量＝くらべる量÷割合
この辺りがアヤシイ人は関連記事「割合まとめ(姉妹サイトに飛びます)」を見ると良いかも
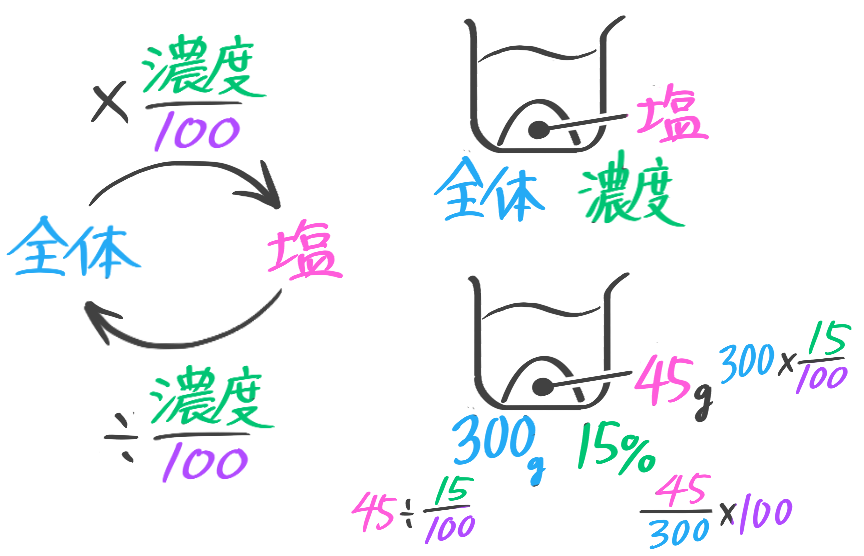
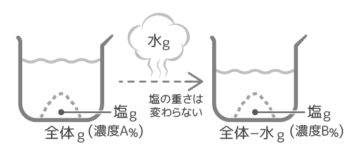
食塩水の図と公式
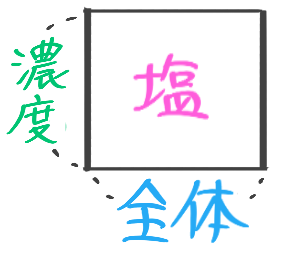
ビーカー図
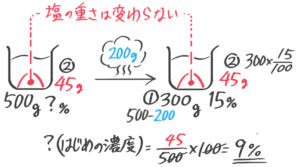
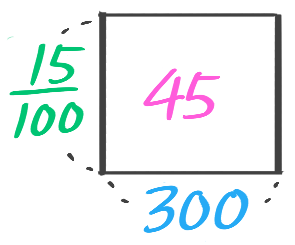
食塩水全体に含まれる塩の量、例えば「15%の食塩水300gに含まれている塩の重さ」を求める矢印図にビーカーや塩の絵をつけると図1のようになります。これを一つにまとめたのが「ビーカー図」(図2)。
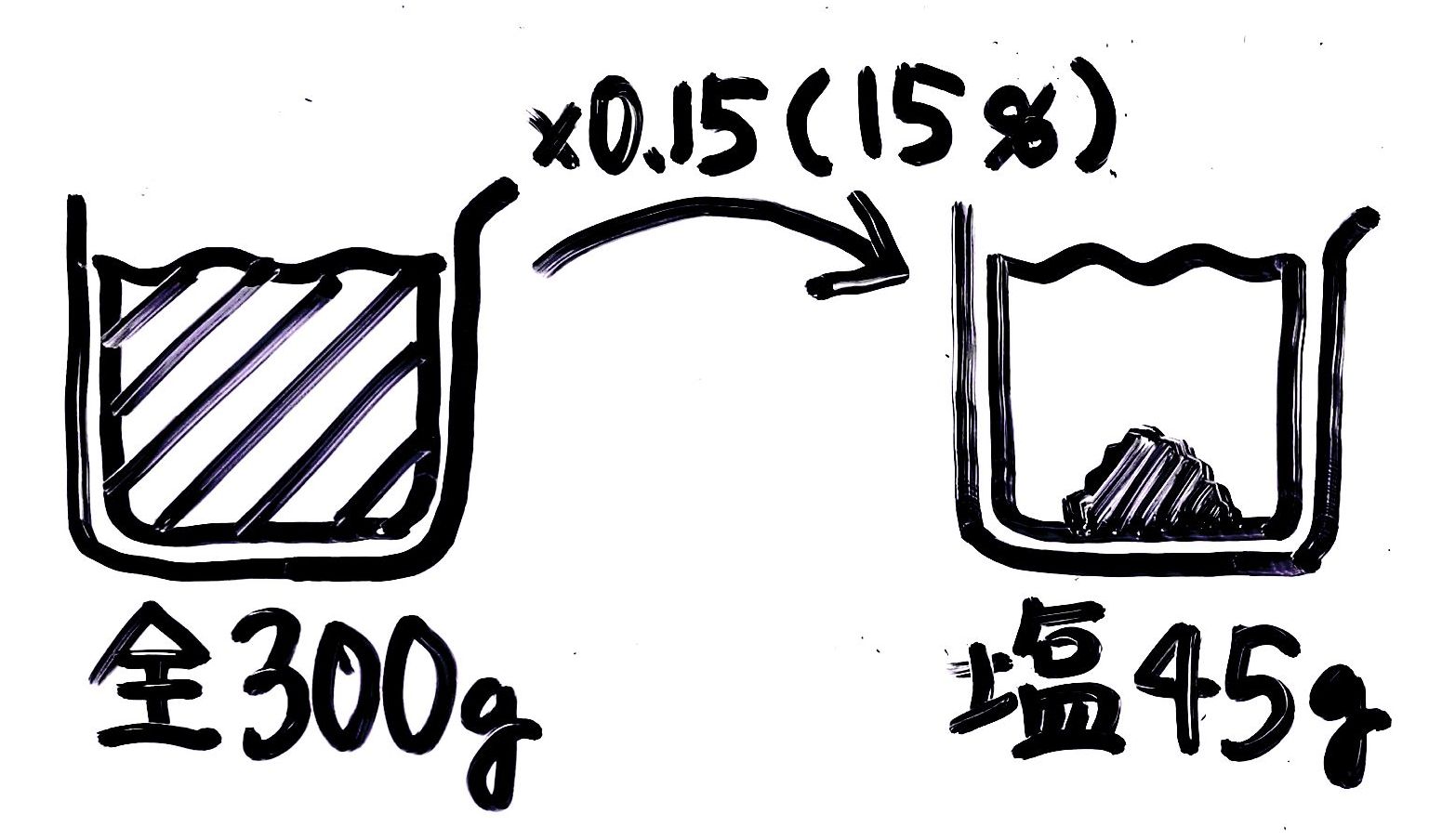
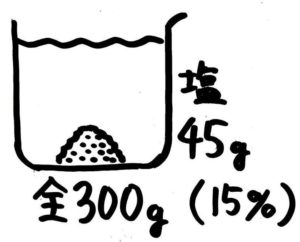
ビーカー図では一つにまとまっている。
食塩水の公式
ビーカー図に登場する三種類の数値「食塩水の重さ」「濃度」「塩の重さ」の関係は割合の三公式の「もとの数」「矢の数(割合)」「先の数」とほぼ同じですが…
➊矢の数=さきの数÷もとの数
❷さきの数=もとの数×矢の数
❸もとの数=さきの数÷矢の数
➊濃さの割合=塩の重さ÷食塩水全体の重さ
❷塩の重さ=全体の重さ×濃さの割合
❸全体の重さ=塩の重さ÷濃さの割合
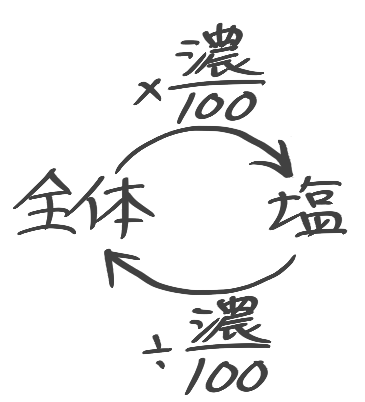
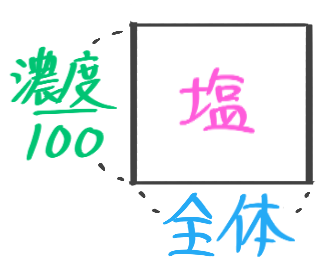
食塩水の濃度(%)は濃さの割合を×100倍したものなので(1%=0.01)、計算に使う時は÷100して「濃度100」の形で使います。また割り算は分数の形にして、プロトタイプの公式を完成させるとこうなります
➊濃度=塩の重さ食塩水全体の重さ×100
❷塩の重さ=全体の重さ×濃度100
❸全体の重さ=塩の重さ÷濃度100
ビーカーの右下に、矢印図を小さくしたものができています(300→(×0.15)→45)。
この公式を覚えれば食塩水の問題はほぼOKなので、理解したら暗唱と書き取りで身につけて下さい。
水の濃度
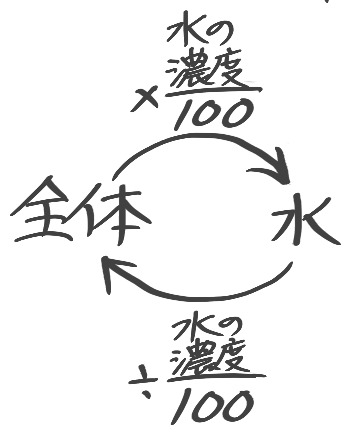
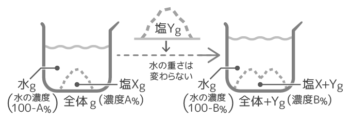
普通は塩の重さに注目して問題を解きますが「水の重さ」に注目する場合もあります。
「水の重さ」は食塩水全体の重さから塩の重さを引けば分かりますね。
さらに「水の濃度」(変な言葉…)を考えます。例えば「濃度15%」の食塩水は全体100%のうち15%が塩なので、残りの85%が「水の濃度」になります。
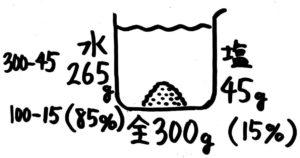
水に注目したビーカー図
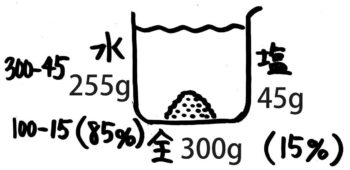
濃度15%の食塩水の
「水の濃度」は85%になる
ビーカーの右下に左向きの矢印図ができているのが分かります。(全体の重さ300g→(×0.85)→水の重さ265g)。
水の重さ・水の濃度を使った公式を作ると、こうなります。水の重さと水の濃度から全体の重さを求める❸が大事です。
➊水の濃度=100－塩の濃度
❷水の重さ=全体の重さ－塩の重さ
❸全体の重さ=水の重さ÷水の濃度100
基本の三公式を覚えた人は、こちらも「作れる」ようにしておきましょう。
その他の図
ビーカー図が描ければ十分ですが、他の図に興味がある人は(開く)を押して下さい
3つの数ABCが「A=B×C」の関係になる時には面積図が出来ました。(詳しくは参考記事「」を見て下さい)食塩水でも「塩」「全体」「濃度/100」が「A=B×C」の関係になっているので面積図ができます。
ただ、食塩水に関してはもう一つ「てんびん図」というのがあって、コチラのほうが直感的に解けて便利です。
もっとも、てんびん図の方は「比(ひ)」という単元を学ばないと使えないかもしれないので、5年の二学期までは面積図を使っても良いでしょう。
食塩水の要素の決定
濃度の公式を使って、三つの要素「全体の重さ」「塩の重さ」「濃度」のうち2つがわかっている場合に、残り1つを出すのが「要素の決定」です
➊濃度=塩の重さ食塩水全体の重さ×100
❷塩の重さ=全体の重さ×濃度100
❸全体の重さ=塩の重さ÷濃度100
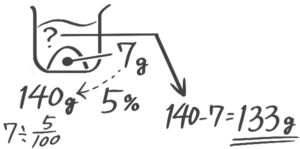
塩を求める
全体の重さと濃度は分かっているが、塩の重さがわからない場合
❷塩=全体×濃度100を使います
X-1:全体,濃度→塩
[予5上6例題1′(2)]
解説
問題文の「濃度3」「全体400」をビーカー図に書く。聞かれている塩は「？」にする
公式❷塩=全体×濃度100より、塩は12gと求められる
これ自体が入試問題になることは少ないのですが、問題に答えるためにこの作業を最初に行います。
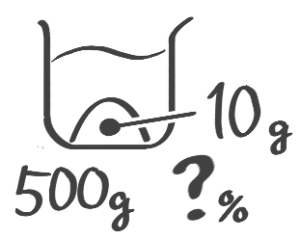
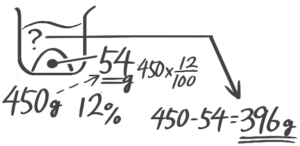
濃度を求める
濃度を求める(全体と塩から)
公式❶濃度=塩全体×100 を使います
X-1:全体,塩→濃度
[予5上6補完例題1-1][予5上6基本問題1(1)]
解説
問題文の「塩10g」「全体500g」をビーカー図に書く。聞かれている濃度は「？」にする
公式❶濃度=塩全体×100 の「塩」に10と「全体」に500を入れて計算し、濃度は2%と求められる
x100を忘れないこと！
濃度を求める(水と塩から)
「塩+水=全体」という関係を利用
X-1:水,塩→濃度
[予5上6例題1′(1)][予5上6基本問題1(2)]
解説
「水の重さ170」はビーカー図の塩の「山」の上のあたりに書き、求める濃度は「？」にする
全体の重さ=塩+水なので200と分かる。
全体と塩が分かれば、公式❶濃度=塩全体×100 で濃度も15%と求められる
X-1:水,塩→濃度
解説
❶濃度=塩全体×100 の「塩」に20を「全体」に200(塩20+水180)を入れて計算します
図:塩と水から濃度を出す
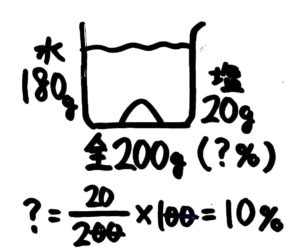
「塩塩+水×100」
水を求める
基本公式では二段階で出します。
X-1:水の重さを求める
[予5上6例題1′(3)][予5上6基本問題1(6)]
解説
「濃度7」と「塩7」をビーカー図に書く
公式❸全体=塩÷濃度100 で全体=140gと出して
塩7gを引けば水133gと求められる
X-1:水の重さを求める
解説
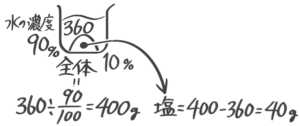
公式❸全体=塩÷濃度100 の塩に「40」を「濃度」に10をいれて計算して「全体」=400g。
全体400-塩40=水360gと分かる
別解
水の濃度は100-10=90%です。塩10%,水90%ということは、塩は水の1/9です。したがって40×9=360gと分かります
X-1:濃度,全体→水,塩
[予5上6基本問題1(4)’]
解説
ビーカー図に「濃度12」「全体450」「塩？」を書く
基本公式「塩=全体x濃度100」から塩を54gと出して
全体450gから塩54gを引いて、水=396gと求められる
食塩水全体を求める
塩から全体を求める
公式❸全体=塩÷濃度100 を使います
X-1:塩→全体
[予5上6補完例1-1(2)][予5上6基本問題1(5)]
解説
問題文の「濃度4」「塩4.8」をビーカー図に書く。聞かれている全体は「？」にする
公式「全体=塩÷濃度100」で食塩水全体は120gと求められる
途中で分数の中に小数が入っていてもOKです。
水から全体を求める
水の濃度を使えば…
X-1:水→全体
[予5上6補完例題1-2]
解説
ビーカー図に「水360」「濃度10」「塩？」を書くが
水と濃度を使った公式は知りませんね…そこで「水の濃度」を考えます！
全体100%のうち塩が10%なので残りの90%が水ですね。この90%が「水の濃度」です
水360gが全体の90%なので、全体は 360÷90100=400g 、塩は 400-360=40g と求められます
別解
食塩水にこだわらず割合で考えると、水90%,塩10%ということは、塩は水の1/9です。したがって360×1/9=40gと分かります
この問題は「水の公式」を使うと簡単です。10%の食塩水の「水の濃度」は100-10=90%です。
➊水の濃度=100－塩の濃度
❷水の重さ=全体の重さ－塩の重さ
❸全体の重さ=水の重さ÷水の濃度100
X-1:要素の決定
[予5上6基本問題5]
解説
ビーカー図に水の重さを書いて…
「水の濃度」は100ー塩の濃度20=80%
解説
水の重さ400と水の濃度80%から全体の重さは500gと求められる。
解説
次に、塩の濃度20%と全体500gから塩の重さも100gと求められる
爽茶これで問題を解く準備が終了しました。
いよいよ問題を解いてみます。
要素の増減
完成した食塩水に水や塩を増やしたり、水を蒸発させて減らしたりします。
考えるコツは
❶2つのビーカー図をつなげた絵を書いて考える
❷増えたり減ったりしていないモノに注目する
です
水を加える(加水)
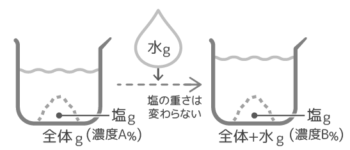
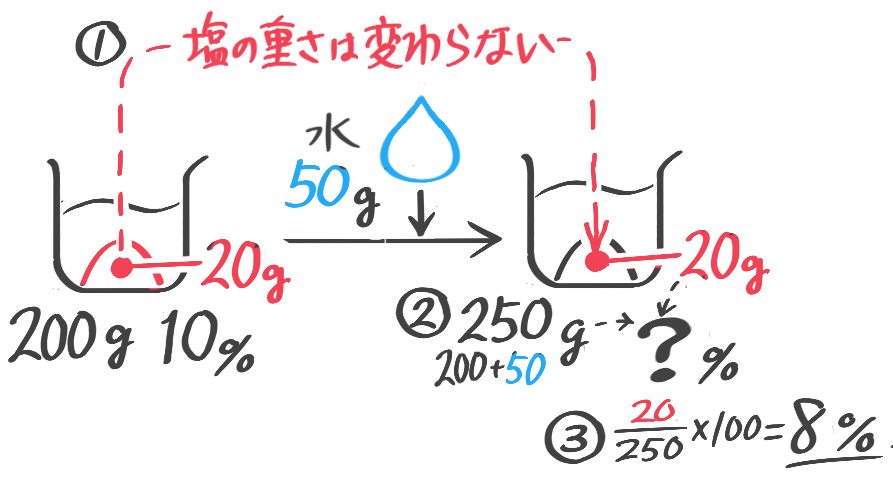
食塩水に真水を加えて薄める(濃度を低くする)場合です。
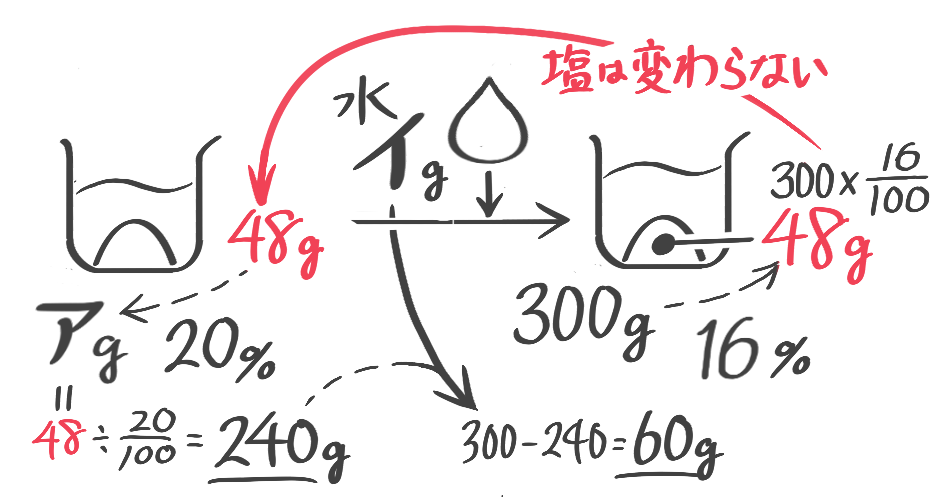
水を加えても塩は変わらないことに注目する
全体の重さは増えますが、塩の重さが変わらないことに注意してビーカー図を書き、公式を使います
濃度Bは「塩全体+加えた水×100」で求められる
濃度を求める問題
X-1:加水後の濃度
[予5上6例題2′(1)]
ヒント
(ここにヒントが入ります)
解説
まずAの塩の重さを 120x10100=12g と出してBe数に書いておく
加水前の食塩水全体が120gで加えた水が80gなので、加水後の食塩水全体は200g。塩は変わらず12g。
ここで「濃度=塩全体x100」の公式を使って、加水後の濃度は12200x100=6%と求められる。
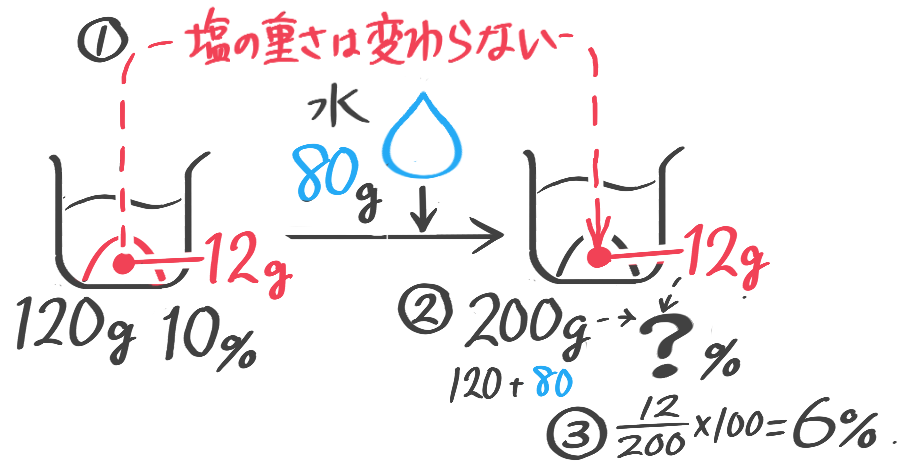
水80gを入れる
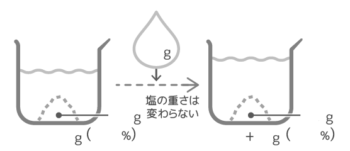
水を加える前後で変わらない
X-1:加水後の濃度
[予5上6基本1(7)]
ヒント
(ここにヒントが入ります)
解説
ビーカー図を書くときに塩の重さは 120x10100=12g と出しておく
水を加えても塩の重さは変わらず20g。全体の重さは50g増えて250gになる
全体250,塩20より濃度は8%と求められる
加えた水を求める問題
X-1:加水量を求める
[予5上6例題2′(2)][予5上6基本2(1)]
ヒント
塩の重さは変わりません
解説
塩の重さは300x8100=24
水を加えた後も塩の重さは変わらず24gで、濃度は3%なので、全体の重さは「全体=塩÷濃度100」の公式を使って24÷6100」=400gと分かります。
水を加える前が300g、後が400gなので、加えた水は400-300=100gです。
数値を変えた類題を解いてみましょう
X-1:加水量を求める
[予5上6例題2′(2)][予5上6基本2(1)]
解説
塩の重さは120x9100=12 x 910=10.8(あとで約分するので、わざと分数にしておいても良い)
水を加えた後も塩の重さは変わらず、濃度は3%なので、全体の重さは「全体=塩÷濃度100」の公式を使って=360gと分かります。
水を加える前が120g、後が360gなので、加えた水は360-120=240gです。
水を入れたら3%になった
水を加える前後で変わらない
X-1:濃度を求める
[予5上6練習4]
ヒント
(ここにヒントが入ります)
解説
ビーカー図で状況をつかむ
加水後の塩=加水前の塩を求めれば、加水前の全体が240gと分かるので
加えた水の重さも60gと求められる
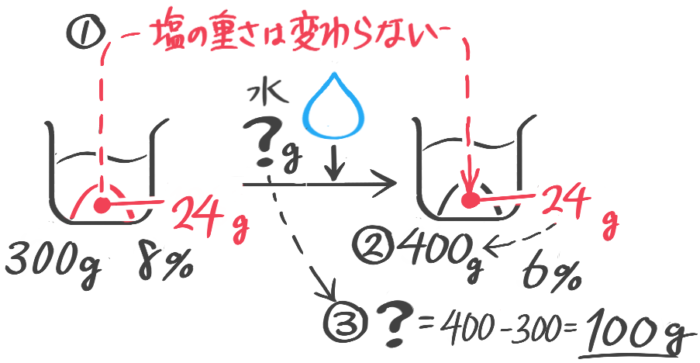
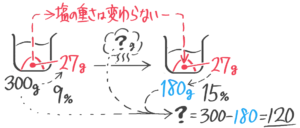
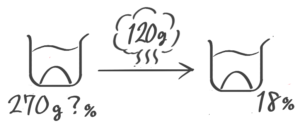
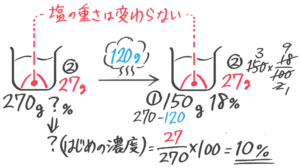
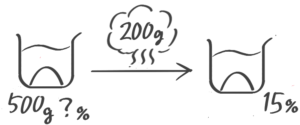
水を蒸発させる(減水)
食塩水を煮ると水だけが減り濃度が高くなります(煮詰める)。
熱して水だけを蒸発させて減らす。塩の重さが変わらないことに注意してビーカー図を書き、公式を使います。
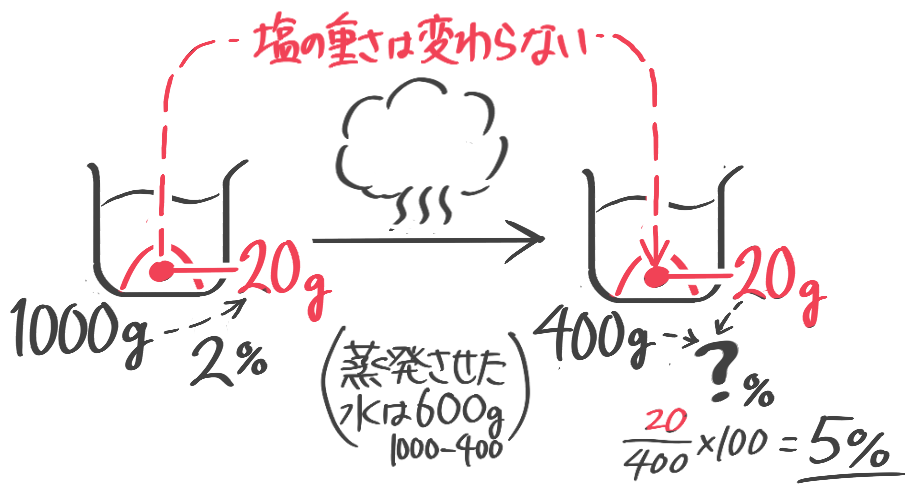
濃度Bは「塩全体-蒸発させた水×100」で求める
濃度を求める問題
X-1:濃度を求める
[予5上6補完例題2-1(1)][基本問題1(8)]
ヒント
(ここにヒントが入ります)
解説
まずAの塩の重さを、1000x2100=20g と出してビーカー図に書き込んでおきます
煮詰めた後の食塩水が400g、塩は変わらず20gなので、後の濃度は、濃度の公式「濃度=塩全体x100」を使って20400x100=5%です。
蒸発させた水量を求める問題
X-1:濃度を求める
[予5上6例題2′(3)]
ヒント
(ここにヒントが入ります)
解説
塩の重さを 600x3100=18g と求めてビーカー図に書き込んでおきます。
水を蒸発させた後も塩の重さは変わらず18g、濃度は9%なので、蒸発させた後の全体の重さは「全体=塩÷濃度100」の公式を使って、18÷9100=200gと分かります。
水を蒸発させる前が600g、後が200gなので、蒸発させた水は600-200=400gです。
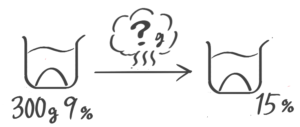
X-1:濃度を求める
[予5上6練習1(1)]
ヒント
(ここにヒントが入ります)
解説
状況をビーカー図にする
蒸発前の塩=蒸発後の塩を出して
公式で蒸発後の全体を出せば、蒸発した水の量も分かる
前の濃度を求める問題
X-1:濃度を求める
[予5上6補完例題2-1(2)]
ヒント
(ここにヒントが入ります)
解説
問題文の状況をビーカー図にする
蒸発させた後の全体は270120=150gなので塩の重さは150×18//100=27と分かる。
そして塩の重さは水を蒸発させる前も変わらず27gなので、濃度は27//270×100=10%と分かります
X-1:濃度を求める
[予5上6基本2(2)]
ヒント
(ここにヒントが入ります)
解説
ビーカー図を書きます
全体の重さが300gに減った全体の重さと濃度15%から塩の重さは45gと分かります
そして塩の重さは減水前も変わらず45gなので、全体500gと合わせて、濃度は9%と求められます。
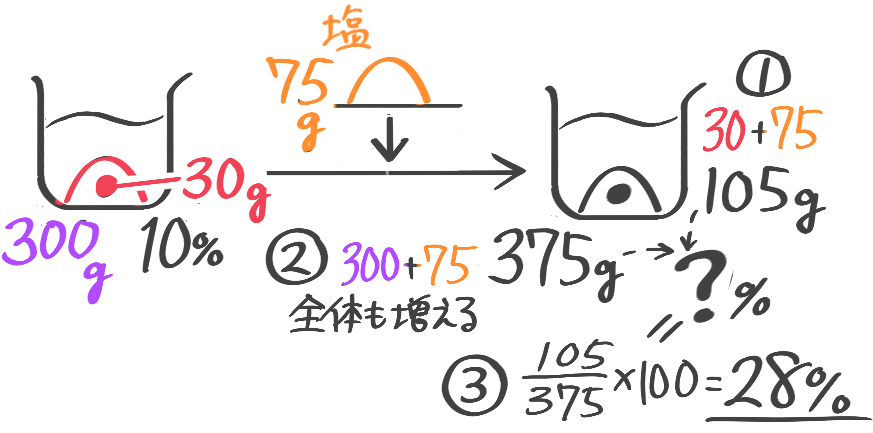
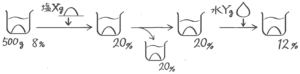
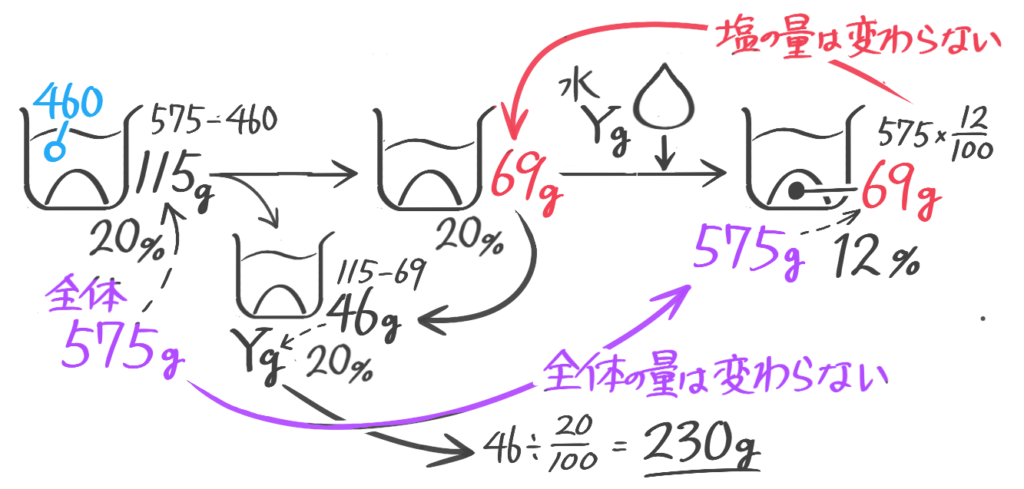
塩を加える(加塩)
塩の場合は「増やす」(濃度を高くする)しかありません。変わらないのは水ですが…
水の重さが変わらないことに注意して
「水の重さ÷100-B100」で全体+Yを求める
濃度を求める
X-1:濃度を求める
[予5上6例題3′(1)][予5上6基本1(9)]
ヒント
(ここにヒントが入ります)
解説
ビーカー図に初めの塩 300x10100=30g を書き込んでおきます。
ここに塩75gを加えると、全体は375g、塩は105gに増えるので(全体も増えることに注意！)、
濃度=105375x100=28%と求められました。
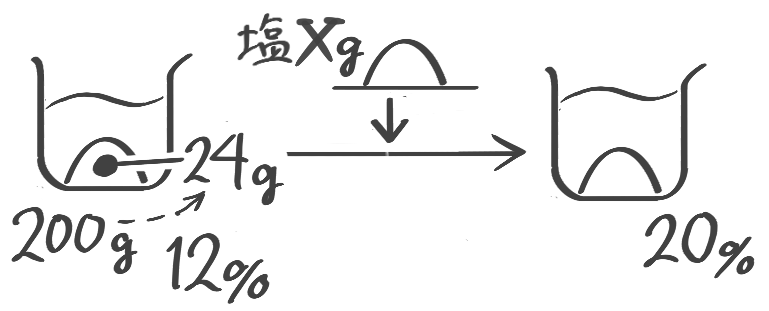
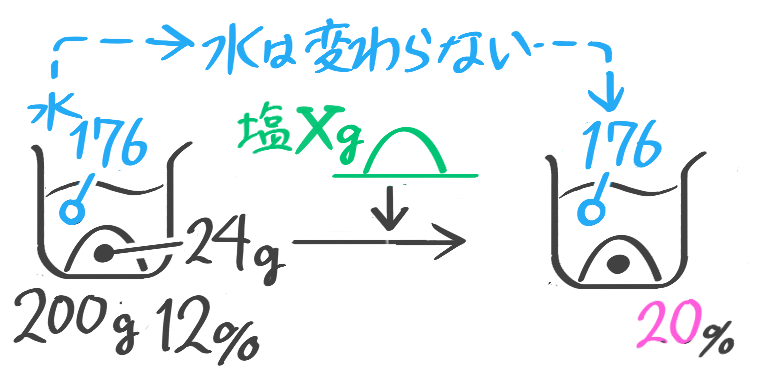
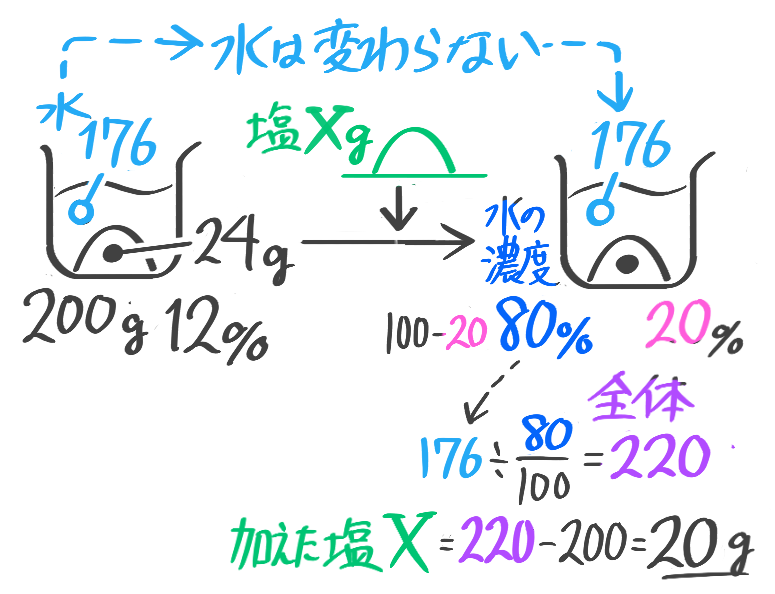
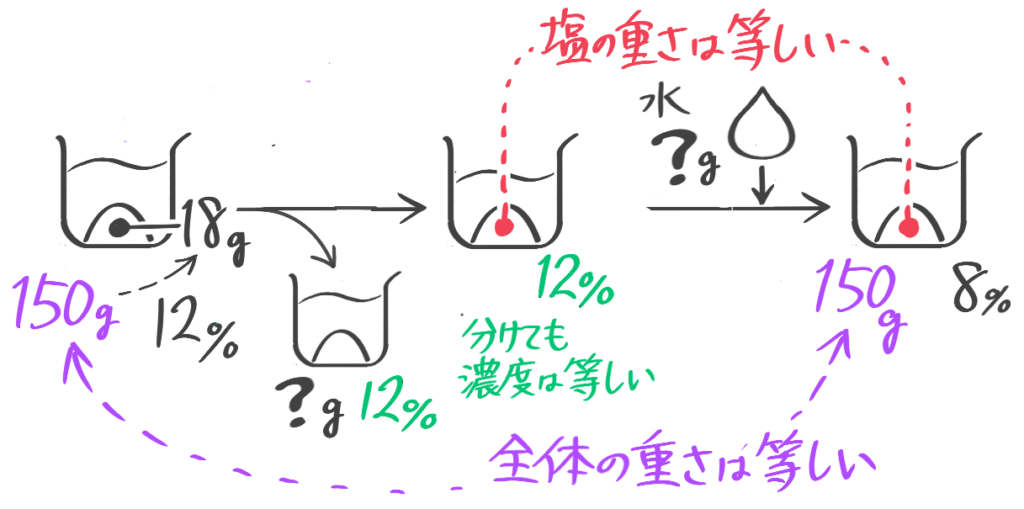
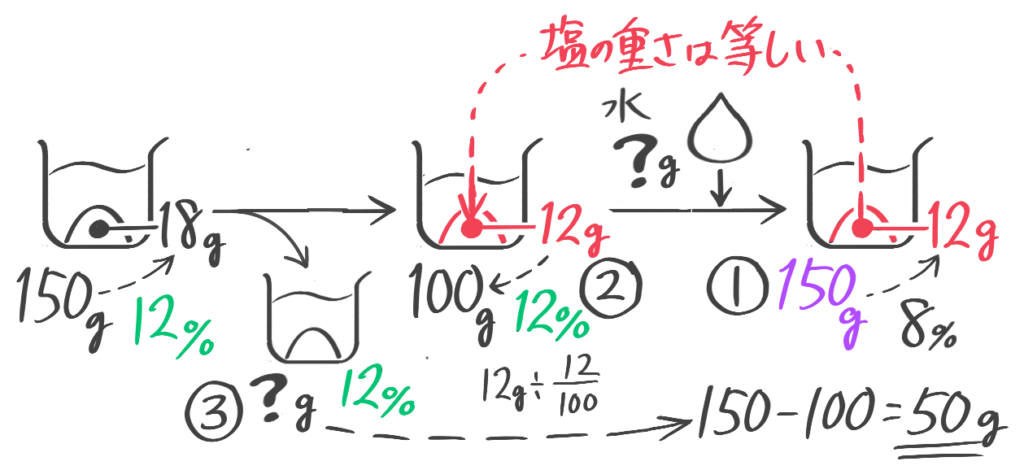
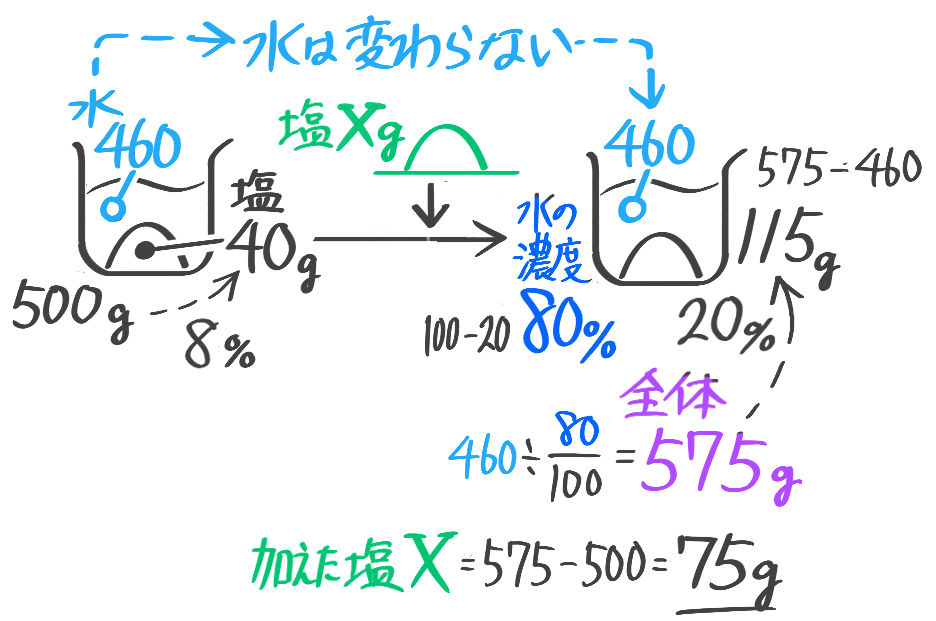
加えた塩を求める
こちらは基本公式だけでは難しいので一工夫必要です
X-1:濃度を求める
[予5上6例題3′(2)]
ヒント
(ここにヒントが入ります)
解説
初めの塩の重さ24gをビーカー図に書きます
水の重さが変わらないので、水の重さを書き込みますが
基本公式ではこれ以上計算ができそうにありません。そこで、上で使った水の濃度の公式をつかいます。
➊水の濃度=100－塩の濃度
❷水の重さ=全体の重さ－塩の重さ
❸全体の重さ=水の重さ÷水の濃度100
はじめの水の量200-24=176gは塩を混ぜた後も変わらず、濃度が20%になると「水の濃度」は100-20=80%になるので、
塩を加えた後の全体=176÷80100=220gで、加えた塩は220-200=20gと分かりました。
この場合は全体の重さも塩の重さも増えてしまうので、「基本(塩の)の公式」は使えません。
一方、水の重さは変わりません。そこで「水の公式」を使いました。
➊水の濃度=100－塩の濃度
❷水の重さ=全体の重さ－塩の重さ
❸全体の重さ=水の重さ÷水の濃度100
面積図やてんびん図を使うやり方
ビーカー図で解けるのであまり必要ではありませんが、面積図や「てんびん図」でも解くことは出来ます。
水を加える場合は、「濃度0%の食塩水との混合」と考え
塩を加える場合は、「濃度100%の食塩水との混合」と考えます
この後、詳しく述べます(→ジャンプ)。
食塩水の1回混合
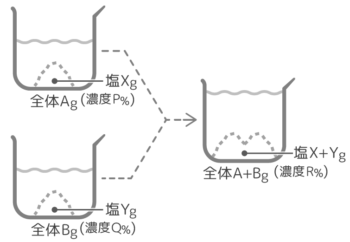
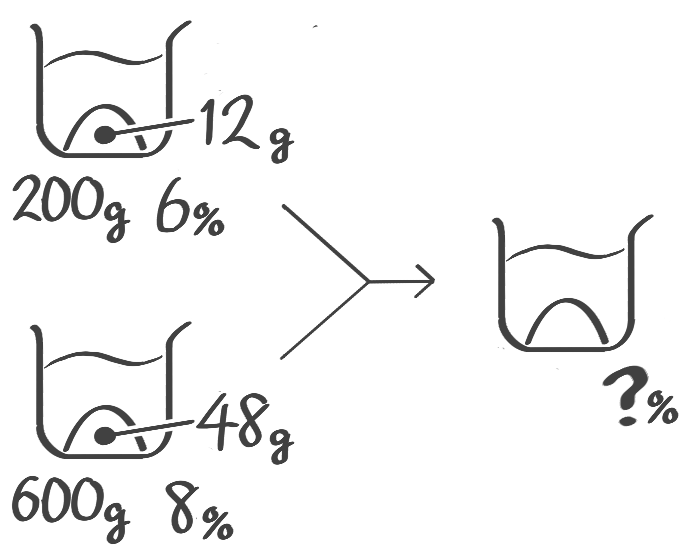
濃度が異なる2つ以上の食塩水を混ぜる問題です。ここからが本番です。
「やりとり算」と同じで、混ぜる前後で塩の重さ,全体の重さの合計は変わらないのを利用できると簡単に解けますが…
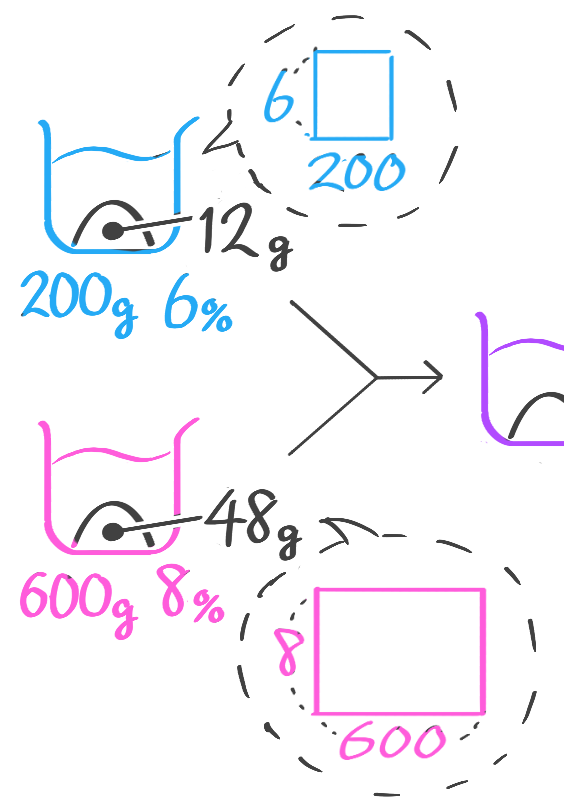
一回混合をビーカー図で解く
登場するビーカー3つのうち、2つの重さが分かっている基本的な問題は、ビーカー図を丁寧に書けば解ける。
濃度は和にならないのに注意する
混合後の濃度を求める
X-1:一回混合後の濃度
[予5上6例題5′(1)][予5上6基本3(1)]
ヒント
(ここにヒントが入ります)
解説
ビーカー図を書きながら塩の重さを出すと、12gと48gなので、
混ぜ合わせてできるのは全体の重さが200+600=800g、塩の重さが12+48=60g の食塩水なので、
濃度は60800x100=7.5%と分かります。
混合前の濃度を求める
X-1:一回混合前の濃度
[予5上6例題5′(2)][予5上6基本3(2)]
ヒント
(ここにヒントが入ります)
解説
2%の食塩水の塩を出しながら、ビーカー図を書きます
合わさった食塩水の全体は450gなので塩の重さは18gです
そこから「さかのぼって」150gの食塩水に含まれていた塩が18-6=12gと分かるので、濃度も8%と求められます
連続作業
2回混合をしたり、混合の前後に作業がある問題
X-1:濃度を求める
[予5上6練習1(2)]
ヒント
(ここにヒントが入ります)
解説
ビーカー図で状況をつかみます。
前半の作業で18%の食塩水150gになり、後半の作業で15%300gの食塩水になると分かるので、
基本混合の考え方で、混ぜた50gの食塩水の中の塩が3g，濃度は6%と分かります。
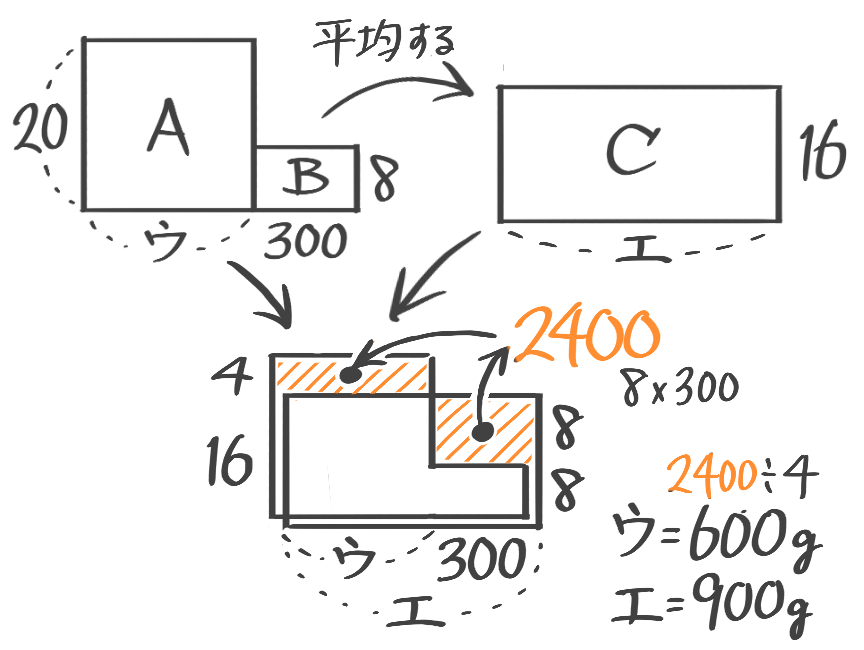
応用混合(面積図)
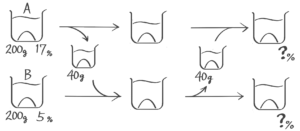
混合に登場する3つの食塩水(ビーカー)のうち、1つしか全体の重さが分からない場合、ビーカー図をどんなに丁寧に書いても解けません。
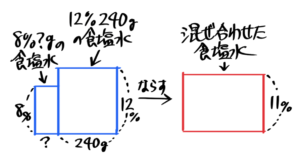
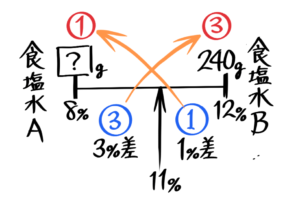
例えば「8%の食塩水□gと12%の食塩水240gを混ぜ合わせると11%の食塩水になった。□を求めなさい」という問題です。
ビーカー図を書いても
((ビーカー図))
8%の食塩水の全体が分からないので塩の重さも分からず、□が出ませんね。
このように全体の重さ(または塩の重さ)が書いていない時は応用図(「面積図」か「てんびん図」)を使いま
てんびん図の方がオススメですが、比を習う前(5年の前期)には面積図を使った解法が出てくるので初めに面積図を説明します
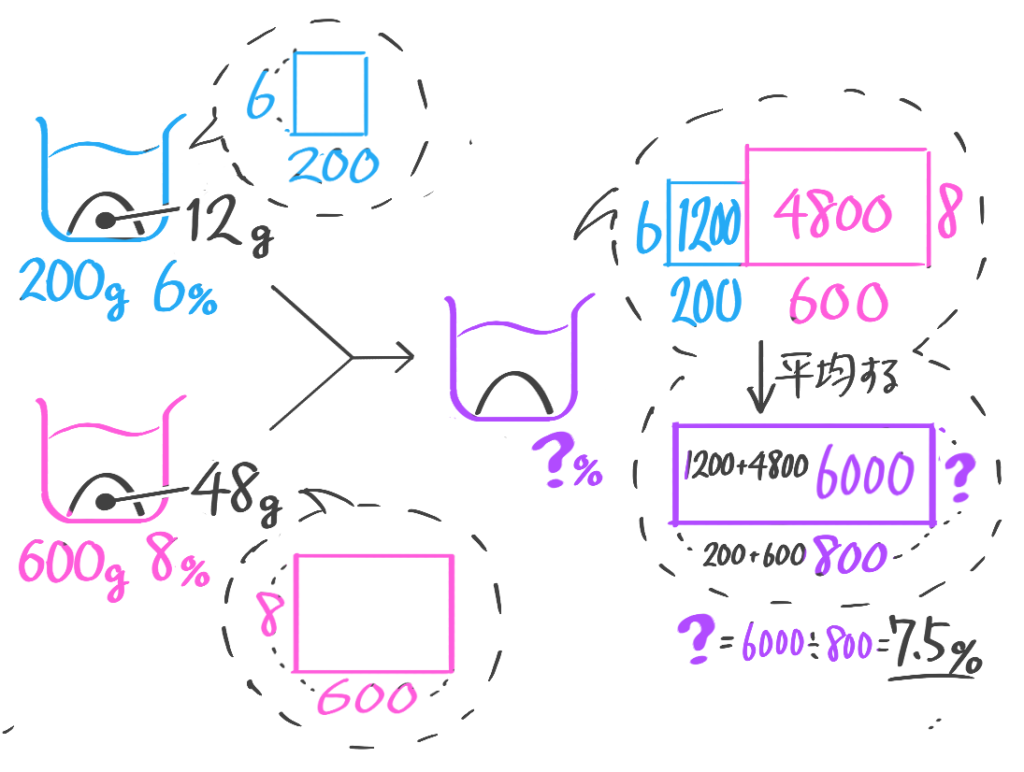
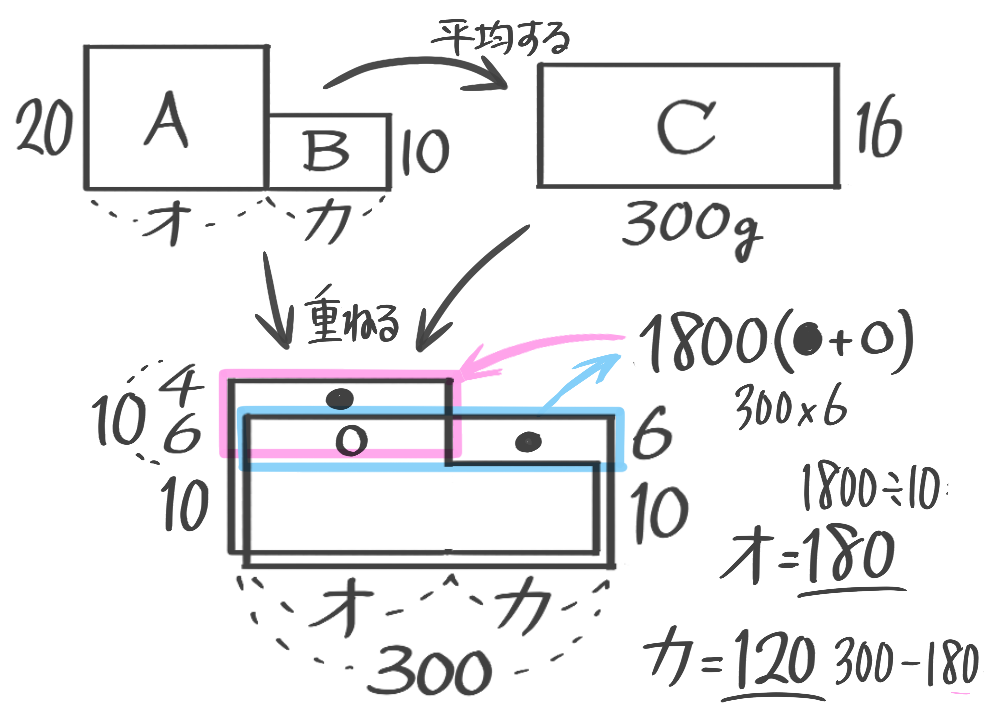
濃度の面積図
平均算で書いた面積図と同じ考え方ですので、習っていない・忘れた人は参考記事「平均算」内の面積図をまず読んで下さい。
X-1:濃度の面積図
[予5上6補完例題6-1(1)]
ヒント
平均算で書いた面積図と同じ考え方
解説
塩=全体x濃度100は45gと求められます。
今の公式「塩=全体x濃度100」を「長方形の面積=縦x横」と同じように考えると、全体が横、濃度100が縦、塩が面積の面積図にできます。
この食塩水の場合は、こうなりますね
ただ混合で使う場合は濃度をそのまま縦にしても解けます(後でコチラを使います)。
次に面積図を使ってみましょう
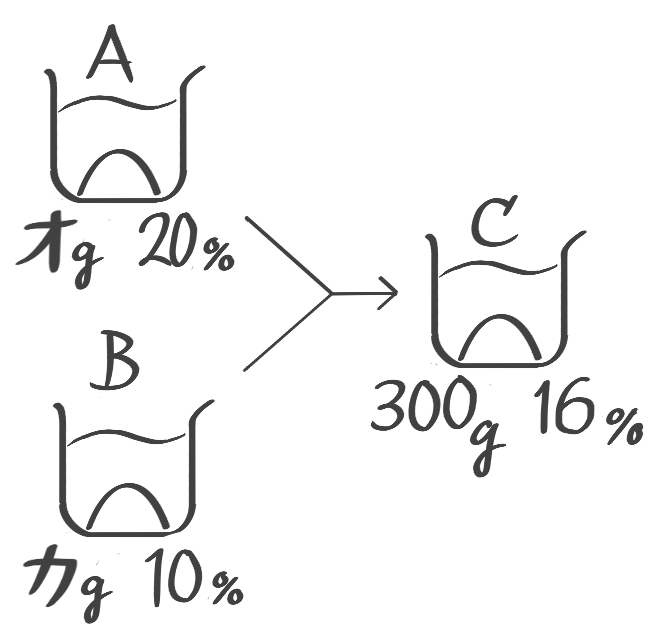
面積図1(はみ出た部分)
混ぜる2つのうちの1つの重さが分かっている場合
まず混合を面積図で表してみましょう
X-1:混合を面積図で表す
[予5上6補完例題6-1(2)]
ヒント
平均算と似てます
解説
ビーカー図はこうでした
200gと600gの食塩水を面積図にします。濃度をそのまま縦にしています。
くっつけるとL字形の面積図が出来て面積は6000です(これは塩を100倍した数値です)。これを平らにならします。
その高さが混合してできる食塩水の高さです。ここでは6000÷800=7.5%と求められました。
この書き方で問題を解いてみましょう
X-1:応用混合(面積図1)
[予5上6例題6′(1)]
ヒント
(ここにヒントが入ります)
解説
2つの食塩水の面積図をくっつけてから、平らにならします
以前「等しい面積の図形を重ねると、はみ出た部分の面積は等しい」と学んだのを思い出して…
ならす前と後の図を重ねて、はみ出た部分(緑色の長方形)の面積が等しいことを利用すると
?=80と分かります
X-1:応用混合(面積図1)
[予5上6練習4(2)]
ヒント
(ここにヒントが入ります)
解説
ビーカー図を書いて状況をつかむと…
全体の重さが1つしか分からず基本混合は無理と分かるので、面積図を書いて重ねて「はみ出た部分●」が等しいことを利用する
ウが600g,エは900gと求められる
X-1:応用混合(面積図1)
[予5上10練習2(2)]
ヒント
(ここにヒントが入ります)
解説
描いているうちにビーカー図だけでは解けないと分かる
A+Bの面積図とCの面積図を重ねて、はみ出た部分が等しいことを利用すると、b=150と分かる
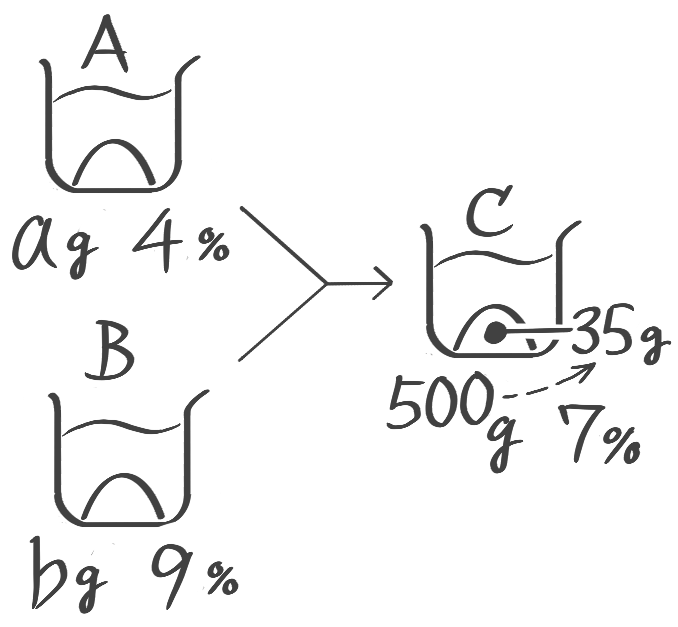
面積図2(はみ出た部分+共通部分)
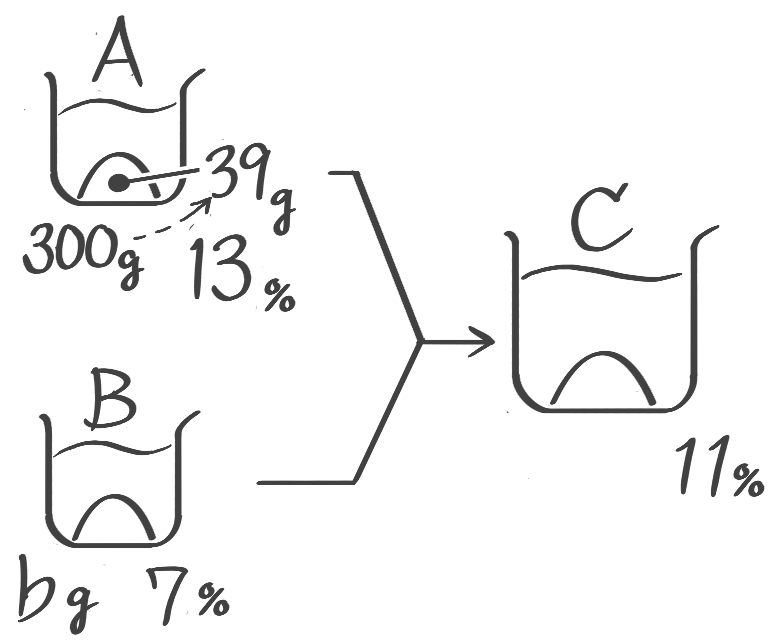
混合で出来た食塩水の重さしか分からない場合「比を使わない面積図」で解くにはさらに工夫が必要です。
X-1:応用混合(面積図2)
[予5上6例題6′(2)]
ヒント
(ここにヒントが入ります)
解説
ビーカー図を書いてみると…これ以上は計算ができないので応用的な図(ここでは面積図)を書きます。
AとBを表す2つの長方形をくっつけたL字形と、それを平らにならした長方形を重ねます
ところが、さっきまでの面積図と違い「はみ出た部分(●)」の面積が出せません。
そこで「○」の部分を共通部分として加え「●+○」が等しいことを利用すると、最初にbが300g、次いでaが200g と分かります。
X-1:応用混合(面積図2)
[予5上6練習4(3)]
ヒント
(ここにヒントが入ります)
解説
ビーカー図を書くと、基本混合は無理と分かるので応用混合の図(ここでは面積図)を書きます
はじめの食塩水が2つとも重さが分からず「はみ出た部分(●)」だけだと比べることができないので、
「○」の部分を共通部分として加え「●+○」が等しいことを利用すると、最初にオが180g、次いでカが120g と分かります
てんびん図(比を習った後)
面積図よりも直感的で便利な図が「てんびん図」です。
((図))
これは理科でならう「てんびん」の考え方を使っています。例えば「支点から6cmの位置に20gのおもりがぶら下げてある時、支点から10cmの位置に何gのおもりを下げればつりあうか」という問題では、支点からの距離と重りの重さが逆比になることを使うと簡単に解けます。
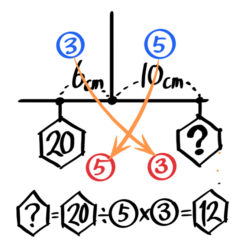
これを食塩水でも利用するのが「てんびん図」です
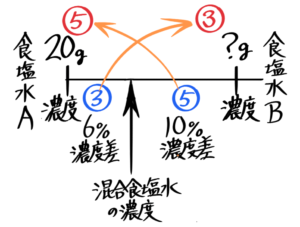
もとの食塩水の「重さの比」が逆比になる
この考え方でさっきの問題を解いてみます。
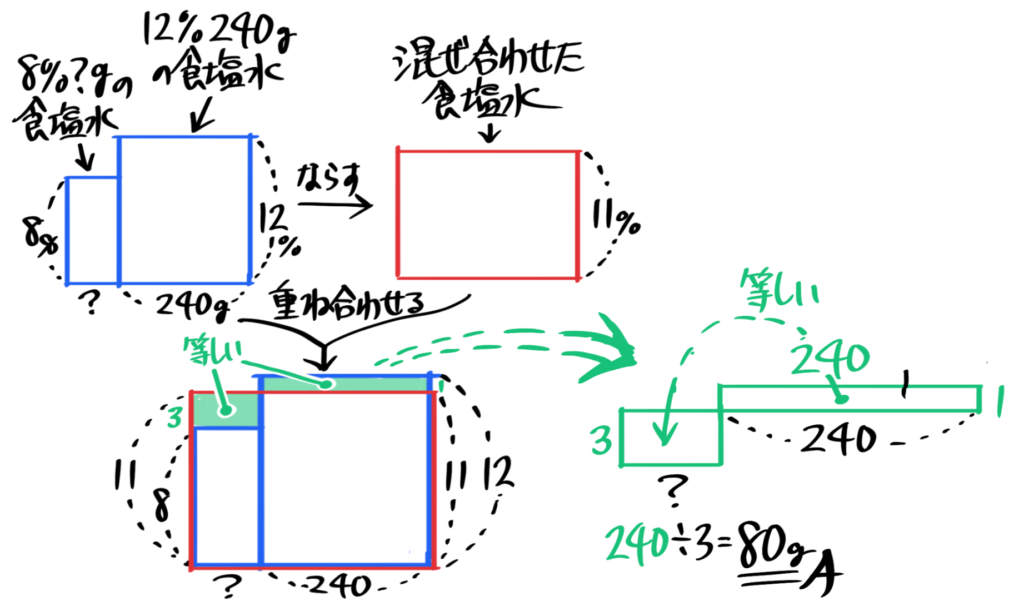
「8%の食塩水□gと12%の食塩水240gを混ぜ合わせると11%の食塩水になった。□を求めなさい」
重さの比は➀:➂になる。
240=➂より➀は80gと分かる
２回以上の混合
２回以上混ぜ合わせる場合は、分かりやすい図を書くのが大切です。以前学習した「やり取り算」を思い出すと良いでしょう。
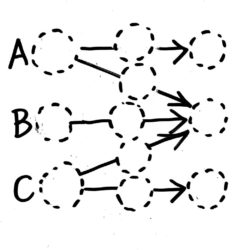
点線マル内に数値を書きます
まず、図だけを各練習を繰り返すのが良いでしょう。
例えば「」の場合の図を書いてみます。
(2021.2.11作成中)
練習問題で定着♪
確認テスト(作成中)
食塩水の置き換え
食塩水の一部を捨てて、同じ重さの水や他の食塩水を入れます。全体の重さが変わらないのがポイント。まずはビーカー図を書きましょう
ビーカー図の書き方
水で置き換え
X-1:食塩水の水との置き換え
[予5上10練習問題2]
ヒント
とにかくビーカー図を書きましょう。考えるのはそれから。
解説
置き換えの性質を思い出しながらビーカー図を書く。
分けても濃度は変化しない、水を加える前後で塩の重さは変化しない、さらに「最初と最後の重さは等しい」
最後の状態での「塩」=12を出せば、真ん中の「全体」=100gと分かるので、捨てた重さは50gと求められる
X-1:食塩水と水との置き換え
[予5上6練習問題3]
ヒント
(ここにヒントが入ります)
解説
ビーカー図を書いて状況をつかみます
前半は「水の濃度」を使って、加塩後の全体の重さを575gと求めれば、加えた塩の重さも75gと分かる
ヒント
(ここにヒントが入ります)
解説
その後、一部を水に置き換えても全体の重さは変わらないので最後の全体の重さも575gのままで、塩の重さが69gと分かり、これは一部を捨てた直後も変わらない。
これで、小分けして捨てた食塩水の塩の重さが46g(濃度は20%のまま)と分かるので全体の重さYも230gと求められる
全体像
他の食塩水で置き換え
食塩水のやり取り
複数の濃度が違う食塩水で「やり取り」をします。まずビーカー図を書けるように練習して下さい
ビーカー図だけで解けてしまうこともありますが、解けない時は面積図やてんびん図を使います。
やり取り算の考え方
①やり取りしても合計(食塩水全体の合計,塩の合計,水の合計)は変わらない
②食塩水は分けても濃度は変わらない
基本やり取り
ビーカー図を書けば解けるものです。
ポイント①「全体や塩の合計は変わらない」を使いましょう
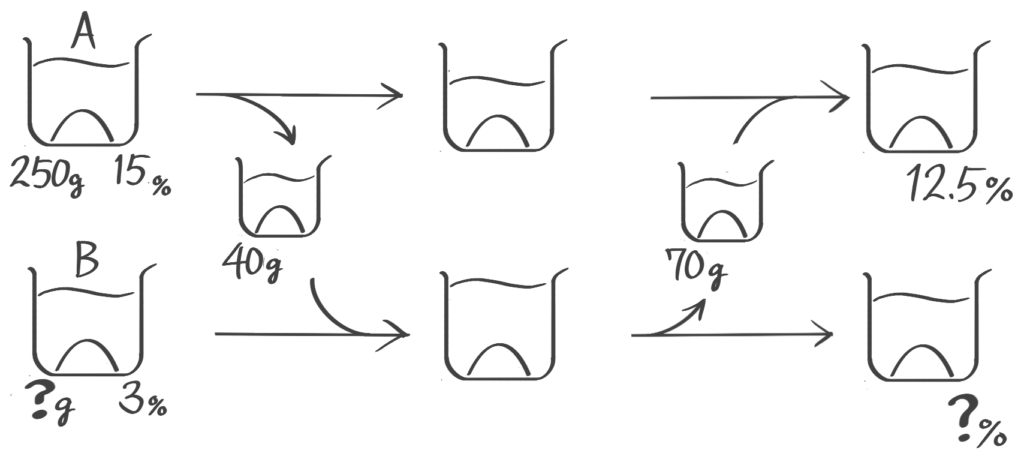
X-1:基本やり取り
[予5上6練習問題2]
ヒント
(ここにヒントが入ります)
解説
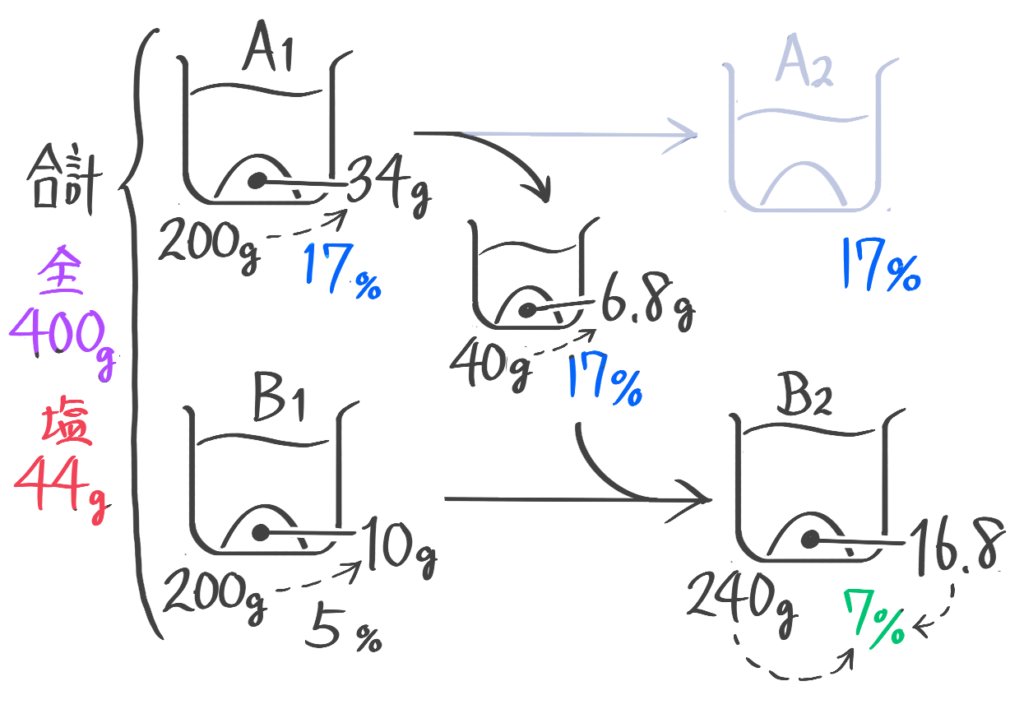
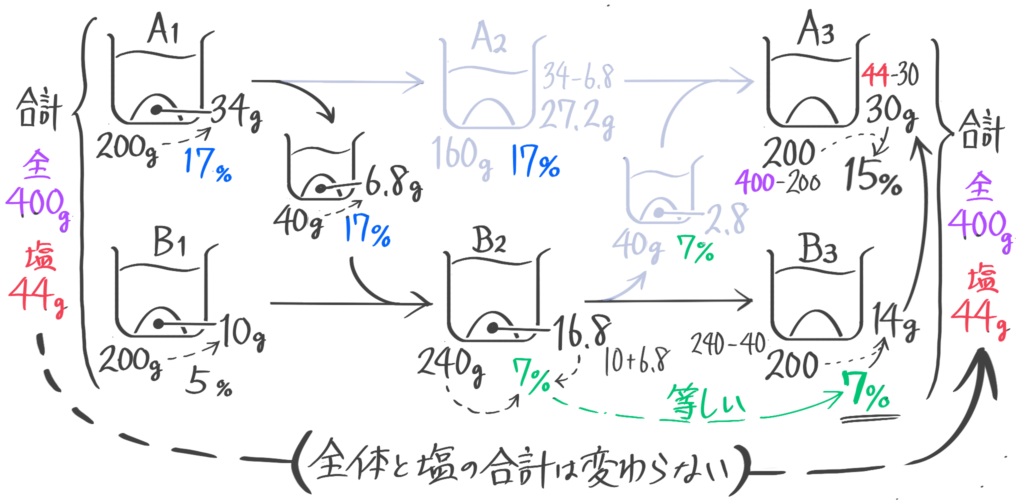
ビーカー図をサッと書いて状況を確認。
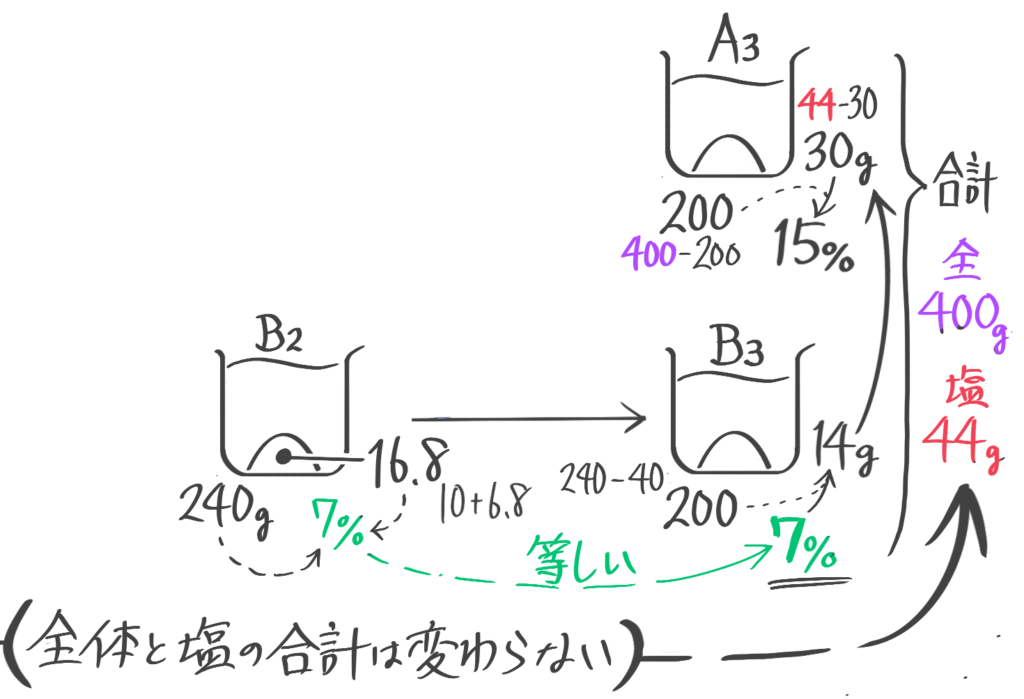
最初の状態(A1,B1)の塩を計算すると、AとBの合計は全体400g,塩44gと分かる
また、等しい量をやり取りするので、AもBも最後は最初と変わらず200gになります。
まず、Aから分けた40gのaとBを混合してできるB2は全体240塩16.8から濃度=16.8240x100=7%と分かります。
ヒント
分かったところを使って答えを出しましょう
解説
その後、小分けして残ったB3の濃度も7%なので塩が14gと分かります。
さらに、全体の合計400gと塩の合計44gからAの最後(A3)の全体200g,塩30gと分かるので濃度も15%と計算できる
(解答の全体像)
Aの途中A2やBから分けたビーカーは全く使わずに解けたのが分かります。
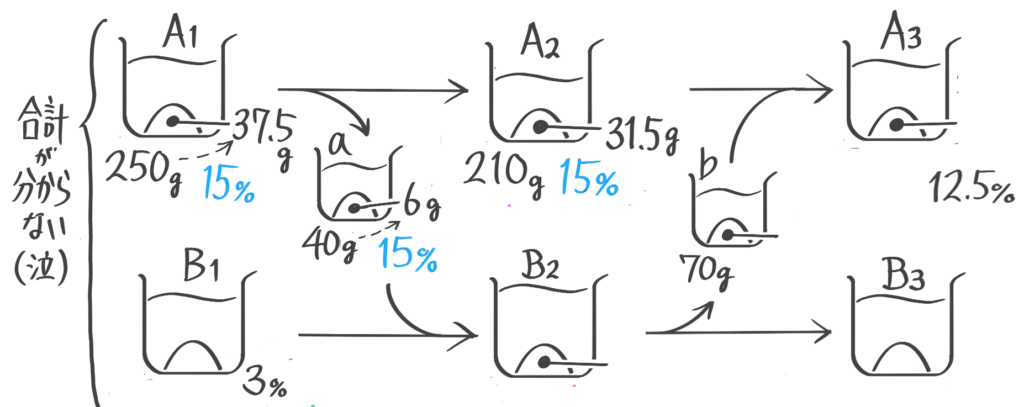
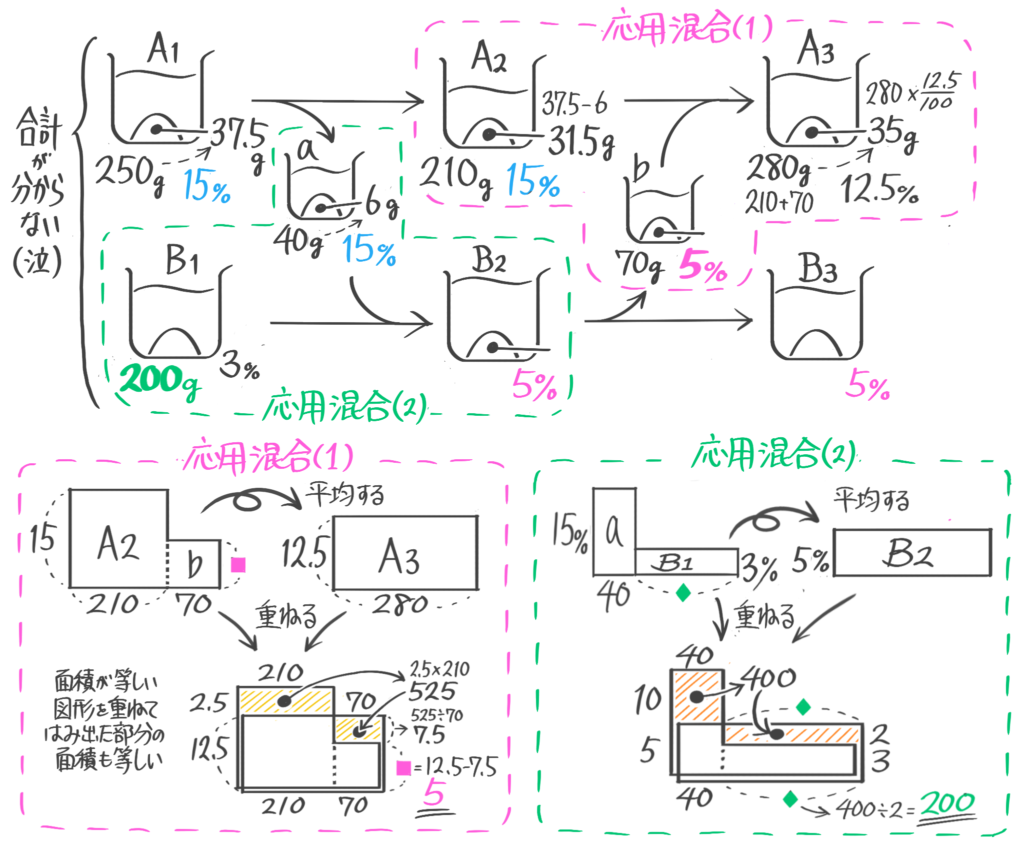
応用やり取り
ビーカー図プラス応用図(「面積図」か「てんびん図」)を使って解くもの
X-1:応用やり取り
[予5上6練習問題5]
ヒント
(ここにヒントが入ります)
解説
ビーカー図を書き「やり取り」と判断する
まず三公式で出せるような数値を全部出してしまう
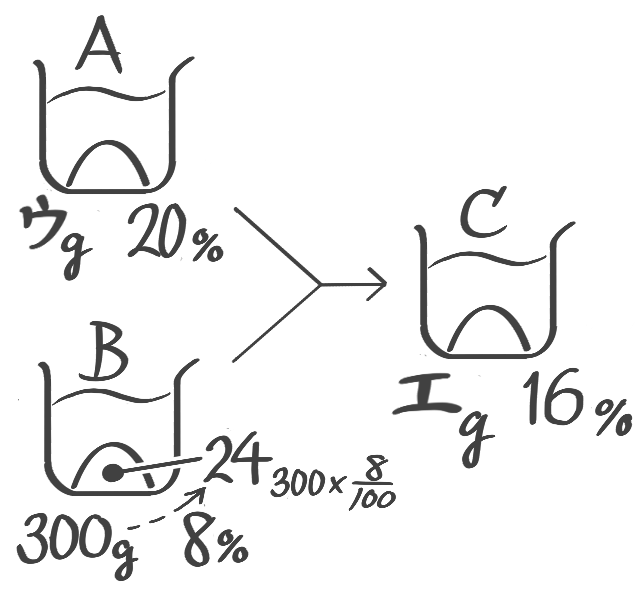
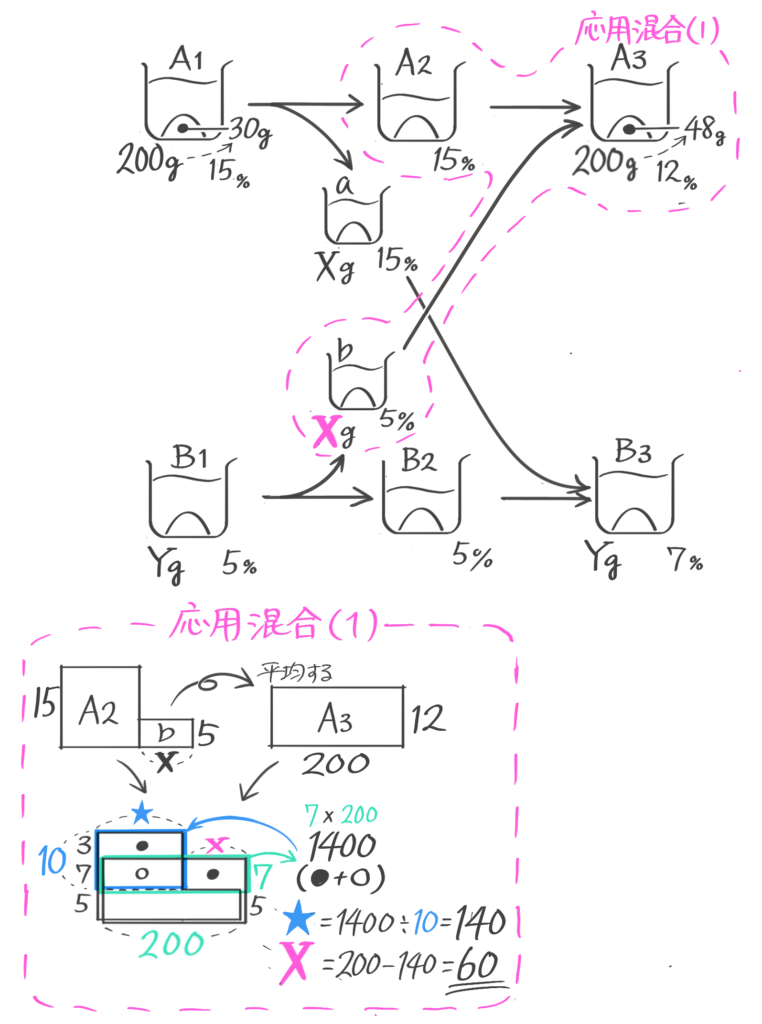
ビーカー図の限界になったので、A2とbを混合してA3を作る部分で面積図を作ってbの濃度を5%と求める(これはB2,B3の濃度でもある)
ヒント
(ここにヒントが入ります)
解説
さらにaとB1を混合してB2を作る部分でも面積図を使ってB1の重さを200gと求めます
次も難しめ…
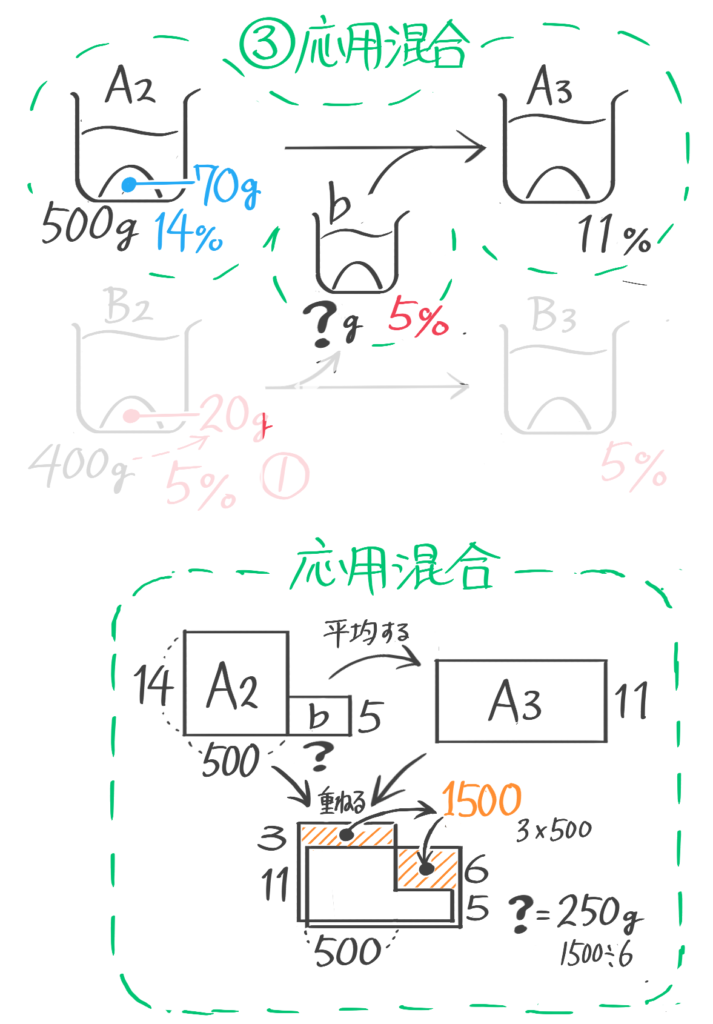
X-1:応用やり取り
[予5上10練習問題4]
ヒント
(ここにヒントが入ります)
解説
計算出来ることを書き込みながら、ビーカー図を書きます。
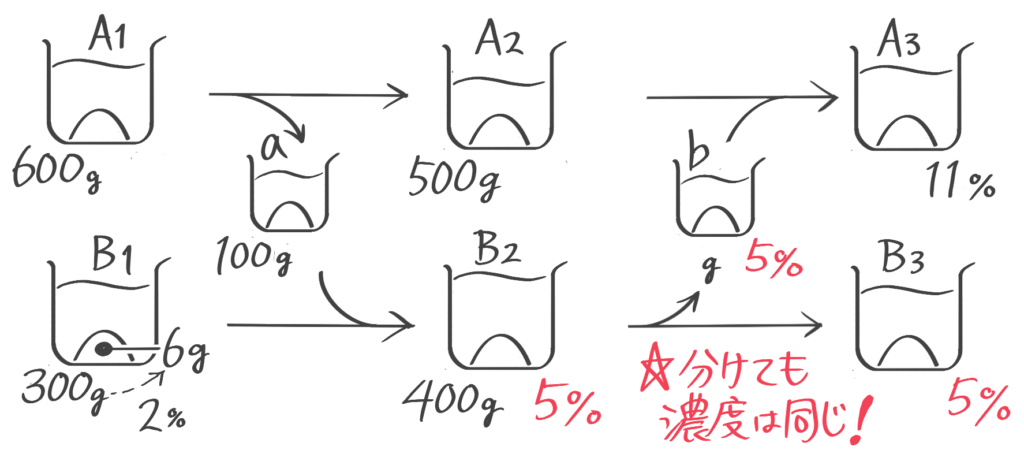
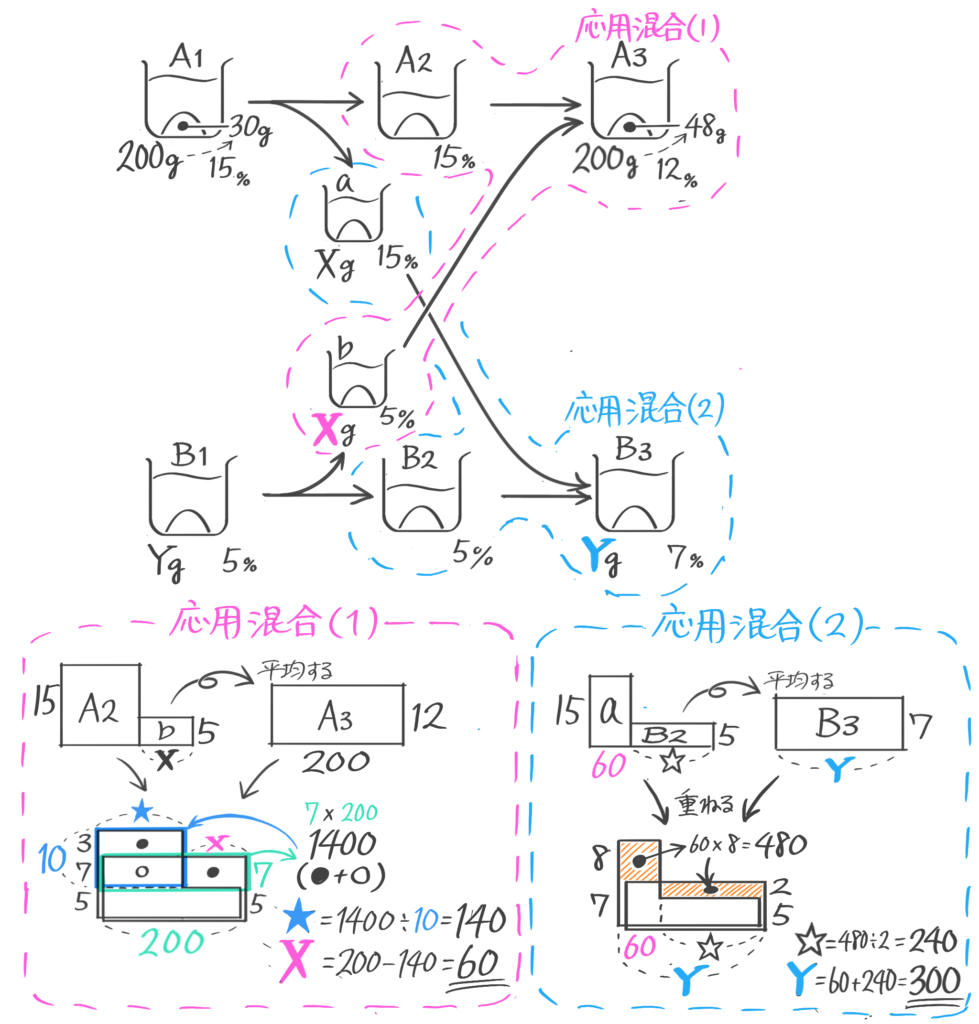
ポイントは、分けても濃度が変わらないのでB2,b,B3の濃度は等しい(5%)ことです。
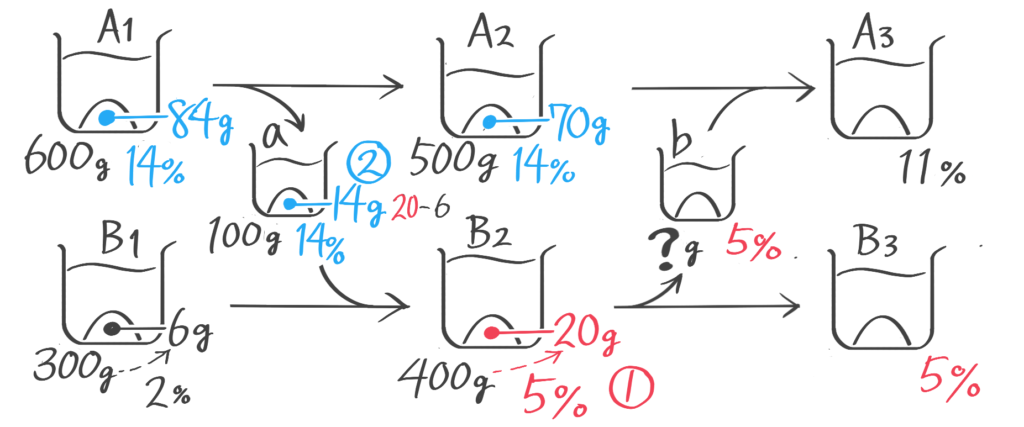
B2が5%400gなので塩の重さが20gで、aに入っている塩の重さは14gと分かるので、a,A1,A2の濃度が14%と分かります。
ヒント
(ここにヒントが入ります)
解説
そこで14%500gのA2と5%のbを混合して11%のA3を作る作業を面積図にしてみます
はみ出た部分が等しいことを利用してbの重さが250gと求められました♪
食塩水のやり取りは以上です
食塩水の交換
「やり取り」は小分けして混合、小分けして混合…を繰り返しますが、「交換」はお互いに小分けしたものを同時に混合します。
ポイントは「やり取り」と同じく
①食塩水全体の合計・塩の合計は変わらない
②食塩水を分けても濃度は変わらない
です
では、さっそく問題を解いてみましょう
基本交換
ビーカー図を丁寧に書けば解けるもの
[補完例題A]
応用交換
ビーカー図だけでは解けないもの
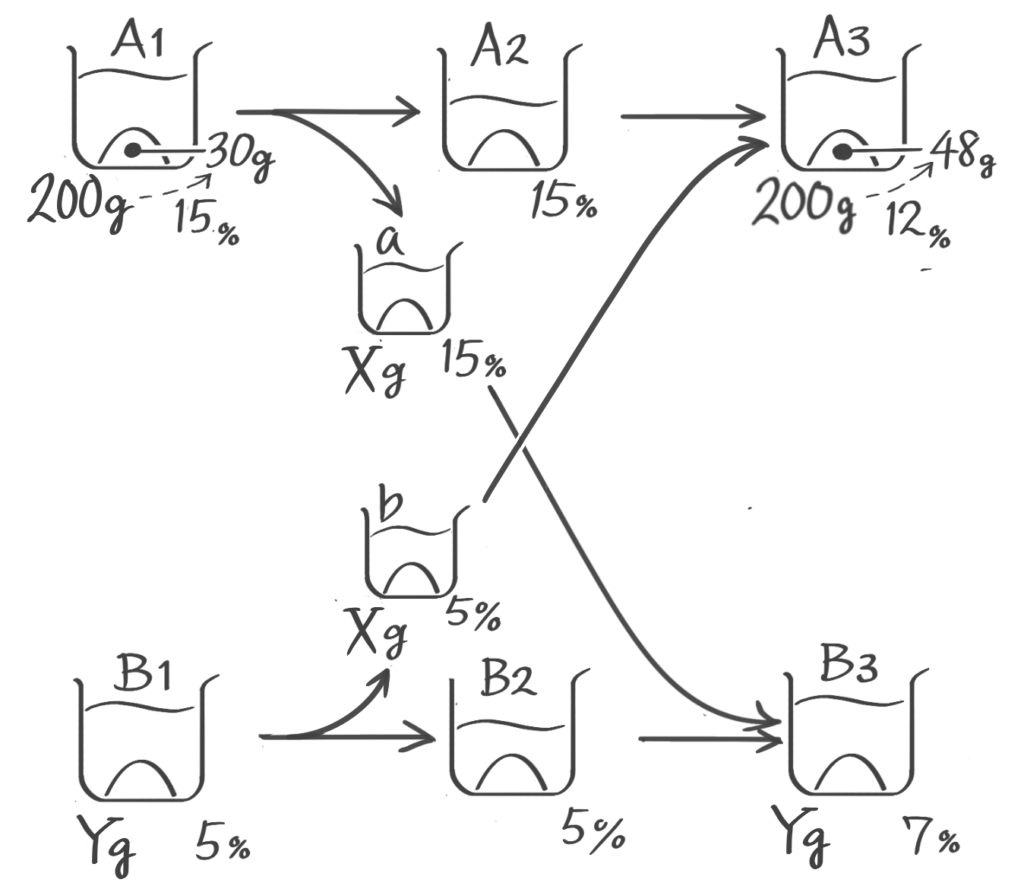
X-1:食塩水の交換(応用)
[予5上6練習問題6]
ヒント
ビーカー図を書いて、どこかで面積図を使いましょう
解説
問題を読みながらビーカー図を書くと「やり取り」ではなく「交換」と分かります。各ビーカーに名前をつけておきます
この問題では2つの混合が両方とも「応用混合」なので面積図を2セット書いて求めます(面倒くさい！)
まずA2とbを混合してA3を作る作業を面積図にすると
bの重さ(X=aの重さ)が60gと分かります。
ヒント
(1)で出したaを使いましょう
解説
(1)で求めたaを使って、aとB2を混ぜてB3を作る作業を面積図にすると
B3の重さ(Y)が300gと分かります
作業の全体像はこうでした(面倒くさかった!!!)
体積の問題
体積が数値に入っている場合
「水に食塩を混ぜても体積は変わらない」という条件がある(頌栄2020-1)
おすすめ教材
爽茶●(濃度だけの問題集は現在調査中…作ろうかな？)
●算数全体の学習もしたい場合
○基本から学習したい人には「算数の基本問題(小5)」(日能研)
○基本は大丈夫なら「算数ベストチェック」(日能研)
○詳しい説明が欲しい人には「中学入試 塾技100(算数)」
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!
保管セクション
rerere
矢印図
→3つの数が「A×B=C」の関係にある時に、
矢印の向きに沿って「A」「B」「C」を並べた図
(例)「2×3＝6」の矢印図
➊さきの数(6)=もとの数(2)×矢の数(3)
❷矢の数(3)=さきの数(6)÷もとの数(2)
❸もとの数(2)=さきの数(6)÷矢の数(3)
れれれ
(15%の食塩水300gに含まれる塩)
(15%の食塩水300g)
(3つの数が右下にまとまっている)
れれれ
➊矢の数=さきの数÷もとの数
❷さきの数=もとの数×矢の数
❸もとの数=さきの数÷矢の数
➊濃さの割合=塩の重さ÷食塩水全体の重さ
❷塩の重さ=全体の重さ×濃さの割合
❸全体の重さ=塩の重さ÷濃さの割合
れれれ
➊濃度=塩の重さ食塩水全体の重さ×100
❷塩の重さ=全体の重さ×濃度100
❸全体の重さ=塩の重さ÷濃度100
れれれ
図1:水に注目したビーカー図
説明書き
れれれ
➊水の濃度=100－塩の濃度
❷水の重さ=全体の重さ－塩の重さ
❸全体の重さ=水の重さ÷水の濃度100
れれれ