中学受験】やり取り算の図の書き方・解き方

「やりとり算って面倒くさい」と思っている中学受験生の方、あなたは和差算や分配算のような線分図を書いていませんか？

じつは「やりとり算」では線分図よりも「やりとり図」を書いた方が簡単に解けるんですよ！

この記事では東大卒講師歴20年の図解講師「そうちゃ」が「やりとり図」を使った解き方を分かりやすく説明します。記事を読んで真似すれば「やりとり算」が解けるようになっているでしょう♪

また「やりとり算」と似ている「ワリカン」の問題もあるのでこれも解けるようにして下さい。

やりとり算の基本

やりとり算=和が等しい

例えば下のような問題です。

1:やりとり算の例

「仲良しのABC三人が36個のアメをテキトーに分けた後、6個しか持っていないBに対してAが4個、Cも何個かのアメを分けてあげたらABCのアメの数がぴったり同じになった。はじめABCは何個ずつ持っていましたか？」

この問題の特徴は、三人の間でだけアメをあげたりもらったりしているのでアメの合計が36個のまま変わっていないことです。

「合計(和)が等しい」のは「やりとり算」を解くのに使うので、必ず覚えて下さい。

「やりとり図」

さっきの問題を実際に解いてみます。

まず、三人の「やりとり」の様子を図にしますが、線分図だとゴチャゴチャして非常に書きにくいです。そこで「やりとり図」を書いてみます。

三人のやり取りなので、三人の名前に続けて横向きに三本の矢印を書いて、矢印の根本と先にに「分けた直後」と「等しくなった時」の数字を書くスペースを作ります。さらにAからBへ、CからBへとアメが移動しているのでその様子も矢印で書き、すべての矢印に数字を書くスペースを作ります。

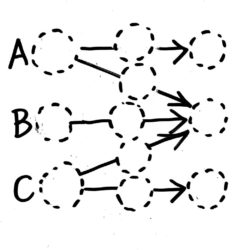
図を使った解き方を理解

今作った「やりとり図」に数字を書いていきます。

➊まず三人でやり取りをしてもアメの合計は36個のまま変わらず、最後は3人のアメの個数が同じになったので、36÷3で最後は3人とも12個になります。これを一番右端の3つの空欄に書き込みます。

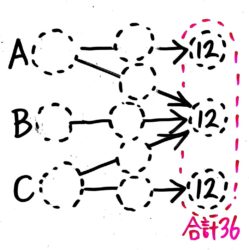
このようにやり取り算は後ろから数字を埋めていくことが多いです。

➋次に、Bははじめの個数6個を誰にもあげていないので、初めのスペースと矢印に6と書き込みます。

➌さらに、AがBに4個あげているのでAからBの矢印に4と書き込みます。

➍またAとCの横向きの矢印は最後の12に一本だけつながっているので12と分かります。

これで問題文の数字は全て書き終わりました。これを見て考えれば答えは出ますね。

初めのAからは12と4の矢印が分かれて出ているので、初めAは12+4=16持っていたと分かります。そして最初も3人の合計は36なので、初めのBは36-6-16=14個と分かります。

A:16個,B:6個,C:14個

このように三人の間(内部)だけでお金のやり取りをする場合には、合計金額(和)が変わらないのを利用して、終わり(右)から初め(左)に「さかのぼって」図を書きます。

やりとり算

❶「和が一定」なことを利用する

❷「さかのぼって」図を書くことが多い

問題で定着

(2020.10.28作成中)

[作成中]割合のやりとり算

受け渡しの量を「○割あげた」○%」のような割合で表現する場合です。

作成中です(2020.10.28)

 

[作成中]食塩水のやりとり算

濃さが違う二種類以上の食塩水の間で行うやり取り算です。

図を書く難しさに加えて濃度の基本計算が加わってくるので、非常に面倒なことが多いです。

まず「食塩水の濃度」をしっかりマスターして下さい。

作成中です(2020.10.28)

 

ワリカン算

(大人の方は知っていると思いますが)「ワリカン」とは、レストランでのパーティーのように何人か一緒にお金を使った時に全部の代金を人数で割って払うことです。

例えば「AB2人で遊びに行って、飲み物売り場でAが二人のジュース代400円を払い、チケット売り場ではBが二人のチケット代2000円を払った」場合、代金の総額2400をワリカン(÷2)した1200円が一人分の代金なので、Aは800円払い足りずBは800円払い過ぎです。そこでAがBに800円払います。これを「精算」といいます。

このような「精算」も二人の間でお金のやり取りをするので「やり取り算」と似ていますが、解き方(図)が異なるので当サイトでは「ワリカン算」と呼ぶことにします。

よく出題される三人のワリカン算を解いてみます。

前置の文章。

2:ワリカン算の例

ABCが映画を見に行って、チケット代金三人分はAが、パンフレット代金三人分はBが、ジュースとポップコーンのセット代金三人分はCが支払った。翌日CがAに800円、Bに200円払って精算は終了した。チケット代金が食事のセット代金の3倍だった時、当日にかかった全費用はいくらか？

まず線分図を「それらしく」書きます。精算の様子から、当日払った金額はCが一番少なく、次がBで一番多く払ったのはAと分かります。またA(チケット代)がC(食事代)の3倍とも書いてあるので、それらを表現します。

次に、一人分の金額を表す線分を下に書きます。この長さは精算時に「払った人(C)」よりは長く、精算時に「もらった人(A.B)」より短くなります。

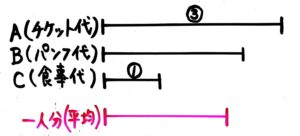
この線を上に伸ばして超えている分が「当日払いすぎて精算時にもらった代金」なのでAは800、Bは200です。一方線が足りていない分がCが精算時に払った代金800+200=1000円です。これらを書き込みます。(書き込んだ数字に合わせて線分図を書き直すことも多いです。)

図が出来上がったら、観察して「丸数字＝数値」を見つけます。ここでは「➁＝1800円」と分かります。

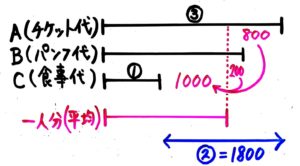
あとはいつもの流れで➀(C)＝1800÷2＝900、➂(A)＝900×3＝2700　と分かります。残りのBの金額も900(C)+1000+200または2700(A)-(800-200)で2100円と分かるので、全代金の合計はA2700+B2100+C900=5700 円になります。

このように、ワリカン算はやりとり算と違って線分図を作って、そこに支払い額の線を引いて解きます。

以上で、「ワリカン算」も終了です。

「やり取り算」と「ワリカン算」は正直に言うと図を書くのがけっこう難しいです。2年間で書けるようになればOKです(汗)

中学受験でお悩みの方へ