「紙のテープやリングをつなぐ問題の解き方を忘れた…」という中学受験生と保護者の方、安心して下さい！
東大卒講師歴20年の図解講師「そうちゃ」が一番簡単な解き方を分かりやすく教えます。読み終えればスラスラ解けるようになりますよ！
テープやリングは
○○算でない方が簡単
こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
テープやリングを「つなぐ」問題を「植木算」の応用としているテキストやサイトが多いです。(単元の順序的にやむを得ない面もありますが)
しかし!植木算の考え方では複雑な計算をしないと答えが出せない場合があります(テープの枚数を求める問題)。
そこで、本サイトでは、どのタイプの問題にも対応できるような植木算では「無い」解法を紹介致します。(植木算の目次は最後にあります)
植木算「でない」解き方！
えっ？「のりしろ」を！？
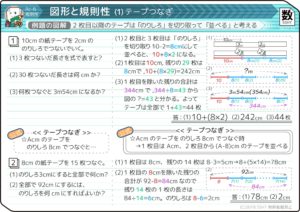
例として、10cmのテープを２cmの「のりしろ」でつないていく場合を考えます。
この問題が面倒くさいのは「のりしろ」があるせいですね。
そこで…思い切って２枚目以降のテープの「のりしろ」を切り取っちゃいます！
そしてつなぐ代わりに、隙間なくピッタリと並べてみます
すると、長さは等しいままで、紛らわしい「のりしろ」は消えました。これで考えやすくなりますね
このように「はじめの１枚はそのまま、２枚目以降は「のりしろ」を切り取って並べていく」と考えるのがコツです。
この問題の場合は、テープからのりしろを取ると10-2＝8cmになるので、テープをつないでいくと合計の長さは「10+8+8+8+・・・」と増え続けていくことになります。
気づいた方もいらっしゃるでしょうが、これは「等差数列」風の考え方です。初項=10,公差=8 ですね。
公式として、カード等の暗記素材にしておくのが良いでしょうね
先頭の一人だけを除いて「カット」してもらい
サッパリしたテープ達
では、上記の考え方で「テープをのりしろでつなぐ」問題を実際に解いていきましょう！
合計の長さを求める
まずはテープの合計の長さを求める問題です
？が求める長さで、？＝10+(8×29)=242cmですね！
テープの枚数を求める
次は、テープの枚数を求める問題です。
？＝344÷8＝43ですが、これは2枚目以降の枚数なので1枚目を加えた43+1=44枚がテープ全部の枚数になります。
わかりましたか？
のりしろを求める
最後は「のりしろ」の長さを求める問題です。
？=84÷14＝6cmで、これはテープの長さ8cmから「のりしろ」を引いた長さなので、のりしろは2cmになりますね。
これでテープの「合計の長さ」「枚数」「のりしろの長さ」のどれを聞かれても答えることができます！(よね？…)
練習問題をどうぞ
爽茶「リング」をつなぐ問題
リングは「●●●」を切り取る
リングを鎖のようにつなぐ問題も、同じ考え方で解けます。
例えば、外側の直径(外径)が8cm、リングの太さが1cmのリングをつなぐとします。
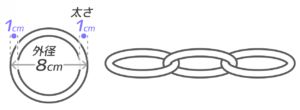
リングの場合、のりしろに当たる部分「つなぎ」は太さの2倍、この場合1×2＝2cmになります
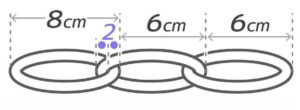
このつなぎのせいで長さがどうなっているのかよく分かりませんね…
そこで、2個目以降は「つなぎ」を切り取ってしまいましょう。するとリング全体の長さは8+6+6+・・・と増えていくことが分かります。
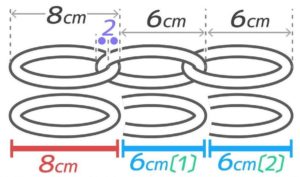
2個目以降はリング-つなぎ2個分になる
それでは、この考え方で問題を解いてみましょう。
はじめはリングの外径も太さも今と同じです。
解き方を理解
2個目以降はリング-つなぎ2個分になる
類題で練習！
次は、リングの太さが分からない問題です。こういう問題では最初に太さを求める小問が出ます。出ない場合は自分で太さを求めましょう。
長さの単位(1cm=10mm)と小数(0.1を10倍すると1になる)を思い出して下さい。
このリングの太さは何mmですか？
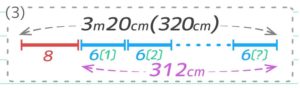
この問題でははじめの1個は外径のまま6cm、残りは外径から太さ2つ分を取った長さ(?とします)なので
6+?+?+? …とつながっていきます。
リング10個だと6cm1個と?cm9個がつながり、これが51cmなので、51cm-6cm＝45cm が?9個分と分かります。
?＝45÷9＝5cmで、これは外径から太さ2つ分を取った長さなので、太さ2つ分＝6cm–5cm=1cmです。
よって、太さ1つは1cm÷2＝10mm÷2＝5mm です。
6+➀5+➁5+…?5 が1m56cm=156cmなので、5×？＝156cm-6cm＝150cm。？＝150÷5＝30個。
よって、リングは全部で30+1＝31個
爽茶「離して並べる」問題
は少し難しい
似た考え方で解く問題がまだあります。それは掲示板に一定間隔で紙を貼っていく問題です。
考え方を理解
例題3-1 幅が8cmの掲示物を2cmの間隔で貼っていく。
(1)7枚貼るのには何cmの幅が必要か？
(2)何枚貼ると1m62cmになるか？
(1)8cm幅の掲示物を2cmの間隔で貼るとこのようになります。
これを、テープやリングと同じように「はじめの1枚」と「残りの全て」の2種類に区切ってみると
はじめの区切りは12cm、2枚目からは10cmの区切りを並べると考えることができます(一枚目は12cm、2枚目からは10cmのテープを貼っていくのと同様)。
従って、7枚貼ると、12cmの区切りが1つ、10cmの区切りが7-1=6つ で、合計の幅は12+10×6=72cmになります。
(2)1m62cm=162cmのうち、はじめの区切りが12cmなので、残りの区切りは合計幅が162-12=150cm、これは150÷10=15個分と分かります。
結局、掲示物は1+15=16枚となります。
間隔が分からない場合
ただ、この「離して並べる」問題の場合はテープやリングと少し違うので複雑です。
テープやリングの場合は1つ目はテープやリングそのものの長さでしたが、掲示物の場合は1つめの長さに間隔が含まれています。
したがって、間隔が分からない場合は等差数列の考え方で単純には解けません。
ただ、間隔が分からない場合は掲示物の数が分かっているはずなので、植木算で解くことができます。
例えば「幅210cmの掲示板に幅30cmの掲示物を5枚貼るとき、間隔を何cmにすれば良いか」という問題の場合
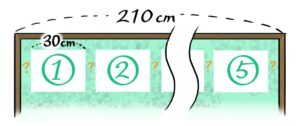
掲示物自体の幅の合計が30×5＝150cm、掲示板の長さ210cmから150cmを引いた残りの60cmが間の長さの合計です。
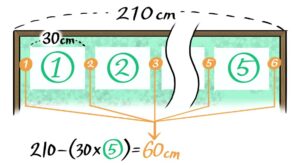
間の数は5+1=6個あるので
間隔=60÷6=10cm
そして掲示物の間の数が5-1＝4、両端も空いているので、間の数は全部で4+2＝6個なので、間の長さ1つは60cm÷6＝10cmと分かりますね。
このように「離して並べる」問題は、図を書きながら「植木算」と「等差数列」のどちらで解くか判断しないといけません。
図を書いて、少し悩めば解けると思いますが…
爽茶まとめ/プリントダウンロード
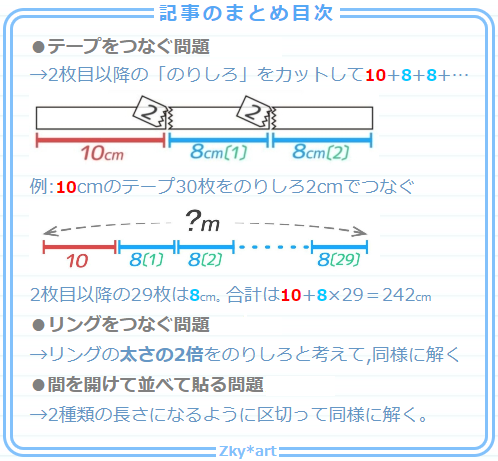
プリントダウンロード
この記事だけでなくサイトで使っている植木算の問題をコチラでまとめてダウンロードできます。
おすすめ教材
「植木算」(サイパーシリーズ)
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!