中学受験生で「平均算の面積図が面倒くさい・難しい」と思っている人がいますが、面積図を使う問題は正しく練習すれば誰でも解けるようになります。
実は、もっとやっかいな問題があります！それは、「平均」という言葉がある問題には線分図で解く問題が混じっていること。
つまり「平均」の問題では面積図と線分図どちらで解くのかを考えないといけないのです…
そこで、この記事では東大卒講師歴20年の図解講師「そうちゃ」が学校で習う平均の基本から、線分図タイプと面積図タイプの見分け方と解き方、度数分布表など平均に関する問題全部を分かりやすく説明します。
この記事さえ読めば、平均算はOK。入試問題だって解けるようになりますよ！
この記事は非常に長いので、目次で好きなところをクリックして好きなところを読んでもいいでしょう。
平均の基礎知識(学校5年)
爽茶念の為、学校でも習う基礎知識を確認します。
分かるよ！という人はジャンプして下さい
平均の意味
「平均」とは、いくつかの数値の「合計」を数値の「個数」で割ったもの。テストの「平均点」でおなじみ？
→いくつかの数値の「合計」を「個数」で割ったもの
平均＝合計÷個数
平均の三公式
「平均＝合計÷個数」から「合計」と「個数」を導くと、こうなります。
●合計＝平均×人数
●平均＝合計÷人数
●個数＝合計÷平均
速さの公式と同じように「かけ算→割り算→割り算」の順で覚えるのが簡単
確認テストをどうぞ。
1:平均の三公式
解説
(4科目の点数の合計を4で割るので、(78+94+57+71)÷4=300÷4=75点
解説
平均72点、回数5回なので、合計=平均72点×回数5回=360点
解説
合計210kg、平均35kgなので、人数=合計210kg÷平均35kg=6人
小まとめ
●平均=いくつかの数値の「合計」を
「個数」で割ったもの
●平均の三公式
○合計＝平均×人数
(例)4科目の平均が75点のとき
→合計点は75×4=300
○平均＝合計÷人数
(例)4科目の合計が300点のとき
→平均は300÷4=75点
○個数＝合計÷平均
(例)テストの合計が300点で平均が75点
→科目数は300÷75=4
この後は、中学受験の「平均算」です
平均算
線分図と面積図どちらで解くか
実は、同じ「平均」という言葉を使った問題でも、解き方は一通りではありません。
なぜなら下図のように、平均の式「平均=合計÷個数」は線分図と面積図の2つに表すことができるので…
平均算には「線分図系」と「面積図系」の2種類の解き方があるのです。
したがって問題を見たら線分図と面積図どちらで解くかを判断する必要がある。図の書き方を覚えても、どちらを使うのか判断しないといけないのが面倒くさい！のです
そこで、最初に判断の基準を理解して下さい。
ザックリ言うと、
①人数が少なかったり(5人以下)、個別の差が書いてある場合→線分図
②人数が多い場合や、個別の差がかいていない場合→面積図
と判断します
具体的な問題文を見たい人は↓(開く)↓をクリックして下さい
①線分図で解く問題の文章
「ABの所持金の平均が650円で、AがBより300円多い…」
「AとBの平均点は66でABC三人の平均点は8点高かった。またAはBより8点高かった…」
「AとBの平均点が84,BとAの平均点が76,AとCの平均点が83…」
「ABCDの平均点が76,ABCの平均点が72,AとDの平均点が75…」
「ABC3人がテストを受けた。Aは平均より2点低く、Cは平均より7点高く、Bの点数は76点だった…」
「ABC3人の平均点は74、AはBより2点高く、CはAとBの平均より15点高かった…」
どれも3～4人しか出てきていませんね？こういうのは線分図で解きます
②面積図で解く問題の文章
「全10回のテストで9回目までの平均が80点だった。最後のテストで90点をとると…」
「全5回のテストで4回までの平均が70点だったのが、最後のテストを受けたら平均が75点に…」
「何回かテストを受けて平均点が73点だったが、最後のテストで100点を取ったので平均点が76点に…」
これらは回数(個数)が分からないか、少ない(5回)場合でも個別の差が書いてありませんね？
または、このような問題
「30人のクラスで、男子16人の平均点が57点、女子14人の平均点が72点…」
「男子が18人、女子が21人のクラスでテストをして、クラス全体の平均は74点、男子の平均は67点…」
「男子25人女子20人のクラスでテストをしたら、クラス全体の平均は75点で男子の平均は女子の平均より9点低かった…」
「あるテストを実施したところ合格者は100人でした。合格者の平均点は受験者全員の平均点より10点高く、不合格者の平均は合格者より14点低かった…」
これらは人数が多いですね？
さらにこのような
「ある印刷工場では、ポスターを印刷してもらうのに枚数によって値段が変わります。10枚までは1枚○円、11枚以上30枚までは1枚●円、31枚以上は1枚◉円で印刷してもらえます…」
このような問題も面積図で解きます
小まとめ
「平均」の問題は、解き方で2つのタイプに分けられます。図の書き方と同時に、解き方の区別を覚えるのも大切です。
では、それぞれの問題の解き方を見ていきましょう
線分図で解く平均算
さらに2つのタイプに分ける
3～4人(個)の数値の平均や個別の差が書いてある場合は線分図を使いますが、図の書き方で更に！2つのタイプに分けられます。
「平均との差」が書いていない場合は、和(合計)=平均x個数を利用して和差算として解きます。
「平均との差」が書いてある場合は平均を表す線を書き込みます(教義の平均線分図)。
●人数が少なく個別の差が書いてある
A:「平均との差」が書いていない→「和差算」
B: 〃 書いてある→平均線を書き込む(狭義の平均線分図)
●人数が多いか個人間の差が書いていない
→面積図を使う
「和差算」タイプ
単純な問題
平均と人数(個数)が分かっている場合は合計も分かるので、和差算の「和」のように書き込みます。
たとえば「A君とB君の所持金の平均が650円」なら、2人の合計(和)=650×2=1300と書き込みます。
さらに差が分かっていれば、和と差が分かるので和差算になります(和差算の解法を知らない忘れた人は「和差算まとめ」を見て下さい)
例題を解いてみましょう
ABの所持金の平均が650円で、AがBより300円多い場合、それぞれの所持金はいくらか？
合計(和)が650×2=1300円、差が300円なのでこうなります。
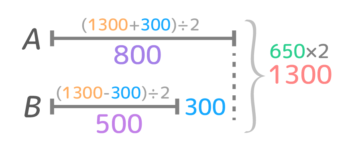
B=(1300-300)÷2、A=(1300+300)÷2でした。
図が出来たらあとは和差算の解法で解けますね()。
もっと問題を解きたい人は、関連記事「線分図で解く平均の問題」を見て下さい。
テストで試してみましょう！
太郎・次郎・三郎の所持金の平均は900円。太郎は次郎より200円少なく、次郎は三郎より100円多い。三人の所持金は？
→( 三量の和差算になる。三人の合計は900×3=2700円。一番多いのが次郎で、太郎は200円差、三郎は100円差。差の部分を埋めて÷3すると,次郎の金額が(2700+300)÷3=1000円。太郎は1000-200=800円、三郎は1000-100=900円。
)
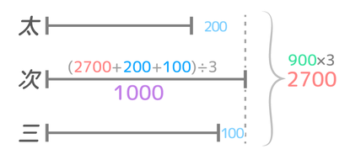平均がいくつか出ている問題
全員の平均だけでなく何人かの平均も分かっている場合はその差で一つの値を出したり、二重の和差算にして解きます。
例えばこんな問題です。
ABC3人がテストを受けた。ABの平均は66点だがABC三人の平均は8点高かった。またAの点数はBの点数より8点高かった時、それぞれの点数を求めよ
AB二人の平均が66点なのでABニ人の合計は66×2=132点、ABC三人の平均が66+6=74点なのでABC三人の合計は74×3=222点と分かります。AがBより8点高いのも書き込みます(図1)。
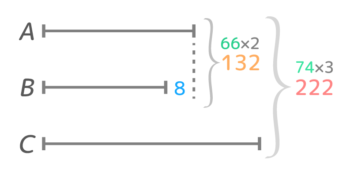
図を見るとABは和差算になっていて、A=(132+8)÷2=70点、B=(132-8)÷2=62点と分かります。(図2)。
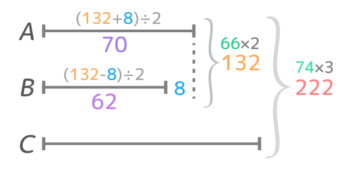
さらに、ABCの合計222からABの合計132を引いた90点がCの得点と分かります(図3)。
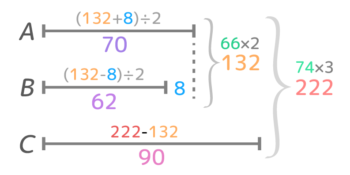
詳しい説明を見たい人は参考記事「和差算まとめ」内「二重の和差算」を見て下さい。
もっと問題を解きたい人は、関連記事「線分図で解く平均の問題」を見て下さい。
全員の平均が分からない問題
全員の平均が分からず何人かの平均しか分からない場合は、和差算で出てきた「和和和算」と同じように式を比べて値を求めます。
例えばこんな問題
3-2-1:平均しかない問題
解説
「合計=平均x人数」を使って、A+B=168,B+C=152,A+C=166 という3つの式ができるので、3つの式の和を÷2してA+B+Cを求めます
(A+B)+(B+C)+(A+C)={(A+B+C)+(A+B+C)}=486
A+B+C=486÷2=243
A+B+C=243とA+B=168,B+C=152,A+C=166の差で、A:91点,B:77点,C:75点と分かります。
もっと問題を解きたい人は、関連記事「線分図で解く平均の問題」を見て下さい。
もう1問
3-2-2:平均しか無い問題
ABCの平均が72点,ADの平均が75点のときAの点数は？
解説
「合計=平均x人数」を使うと式が3つできます
①A+B+C+D=76×4=304
②A+B+C =72×3=216
③A +D=75×2=150
これらを見比べて…
①-②でD=304-216=88点
③よりA=150-88=62点と分かります。
ちなみに、この問題ではBとCの点数は分かりません
次は「和差算」タイプの問題は以上です
平均線を書くタイプ(狭義の線分平均算)
問題文に「平均との差」が書いてある場合は、線分図に平均を書き入れます。2つの書き方(2-1と2-2)があります。
書き方1(ワリカン算)
自分を含む平均との差が書いてある場合、L字で各線分の中ほどを縦断するタテの線として平均を書きます。
線分が二本の場合は平均のタテ線と各線分の差は等しくなり(図1)、
平均は線分を横切るタテ線になり、
赤と青の長さは等しい
線分が三本以上の場合は平均より高い部分の合計と低い部分の合計が等しくなる(図2)。
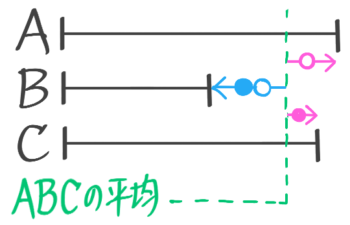
線分が三本以上の場合、赤の合計と青は等しい
これは「ワリカン算(ABC3人が遊園地に行ってAが乗り物代全部をBが食事代全部をCが交通費全部を支払い、翌日に清算した…みたいな問題)」の書き方です。
この図を頭に入れて、例題を解いてみましょう
3-3-1:平均(ワリカン)
解説
Cの平均との差が+7、Aの平均との差が-2なので、上記の関係を思い出すと、Bは平均との差が-5と想像できます。
高い部分は等しくなるハズ
よって平均点は76+5=81点と分かります
平均点は81点
分かりましたか？もう1問どうぞ
3-3-2:ワリカン算タイプ
4つの数ABCDは、ABCの平均とAが等しく、BCDの平均とBが等しい。DがAより48大きいとき、CとDの差はいくつか
ABCの平均とAが等しいので、Aの右端をL字の縦とそろえる
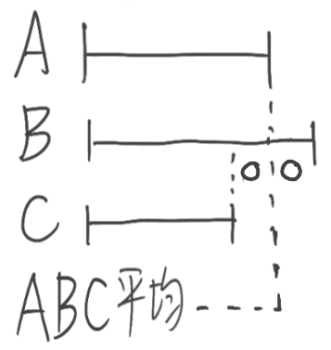
AとBの差(○)とAとCの差(○)が等しいと分かる。
さらにBはBCDの平均と等しいので
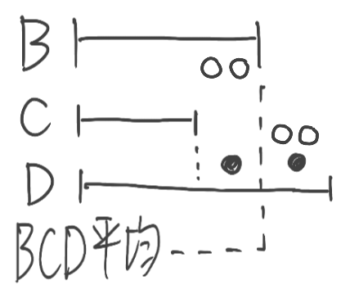
BとCの差(○○)とBとDの差(○○)も等しいと分かる
そしてADの差が48なので…
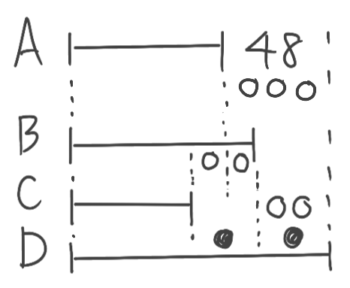
○○○=48と分かり、○=16です。
したがってAとCの差(○○○○)は16×4=64です
もっと問題を解きたい人は、関連記事「線分図で解く平均の問題」を見て下さい。
書き方2
自分を含まない平均との差が書いてあるこんな場合です
1-1:サブタイトル
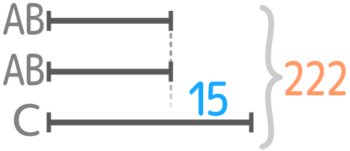
「CはABの平均より15点高かった」この部分に注目して下さい。Cと自分を含まないABの平均との差が書いてあります。
こういう場合は、「ABの平均」の線分を2本書いてしまうと良いでしょう。
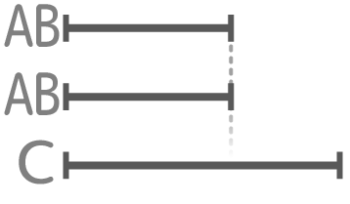
といてみましょう。
3-3-2:平均線分図(II)
解説
3人の合計点は74×3=222点は分かるが、これ以上の具体的な点数は分からない
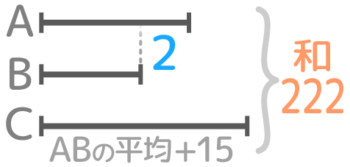
AとBを2人の平均「AB」2本の線として書くとこうなる(ABの差は後回しにする)
3量の和差算を解いて、C=84、ABの平均=69と分かる
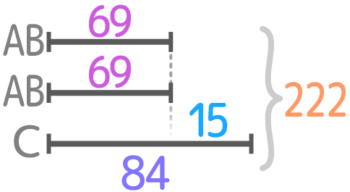
ABの合計=ABx2=69×2=138になるので、AとBは和138、差2の和差算になる
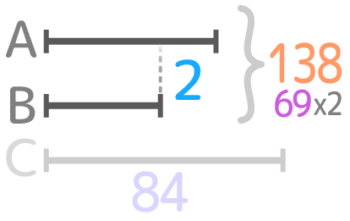
これを解いて、A=70,B=68とわかります
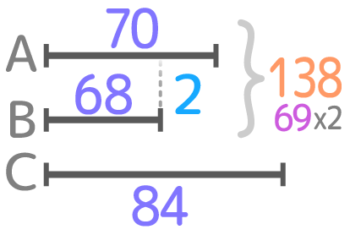
もっと問題を解きたい人は、関連記事「線分図で解く平均の問題」を見て下さい。
平均算の線分図解法は以上です。
面積図で解く平均算
人数が多い場合は面積図を使います。
●人数が少なく個別の差が書いてある
→線分図を使う
●人数が多いか個別の差が書いていない
→面積図を使う
面積図の基本
面積図の作り方
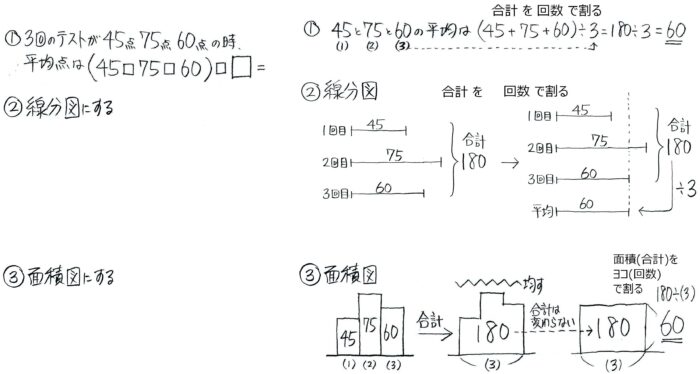
全4回のテストを受けたところ78点,94点,57点,71点だった場合、点数を棒グラフにすると凸凹になります(図1→図2)。
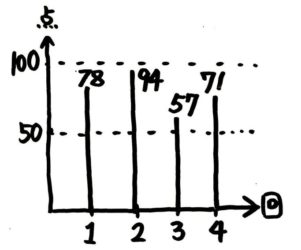
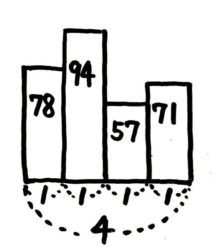
この凸凹をならすと長方形になります(図3→図4)。そして形を変えても面積(合計300)と横幅(4)は変わらないので高さが300÷4=75 と分かります。
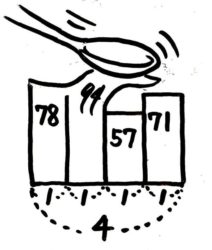
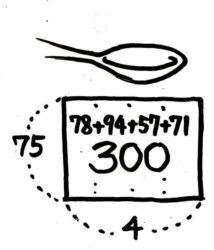
これが平均算の面積図です。長方形の面積が「合計」、タテが「平均」、ヨコが「人数(個数)」になります。
●平均＝合計÷人数
●個数＝合計÷平均
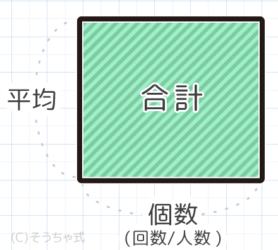
最初に公式の一番目を「合計＝」にしたのは、面積図が書ける公式を覚える際には面積にあたる用語を最初にするのが覚えやすいからです。(参考記事「単純な面積図」)
また幅1の長方形は線分と同じなので、線分図の代わりにもなります。
面積図の重ね合わせ
平均算の応用問題では面積(合計)が等しい二つの面積図を重ねて考えることがあります。この時、重なっていない部分の部分の面積が等しいことを利用します
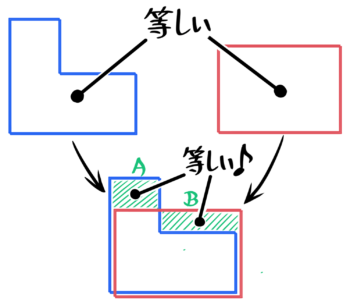
詳しくは参考記事「重なる面積図」を見て下さい
爽茶ここからは受験で出題される平均算をタイプ別に見ていきます。
「最後のテスト」
何回かテストを受けて最後にもう一回テストを受けるような問題です。使う式はこちら
合計点数＝前回までの合計+最後の点数
=(前回までの平均×前回までの回数)+最後の点数
公式の使い方・図の書き方
一番簡単な問題で公式と図を使う練習
1-1:最後のテストの面積図
解説
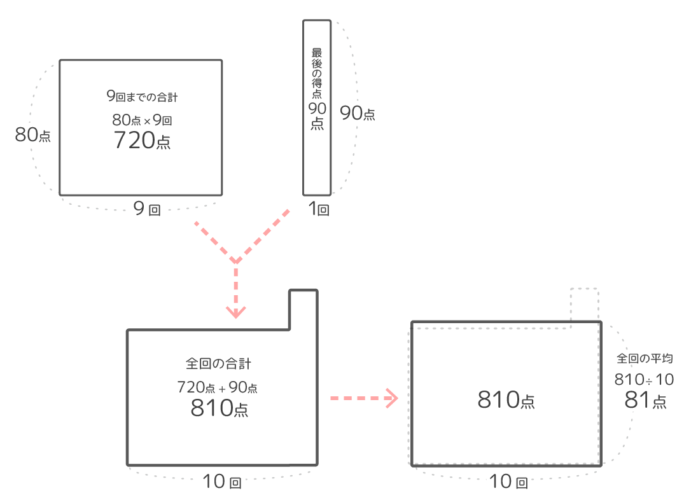
今までの回数と平均から80×9=720の長方形の面積図を書き(図1)。右端に最後のテスト(1×90の長方形)をとりつけます(図2)。この時の合計は80×9+90×1=810点になっています。
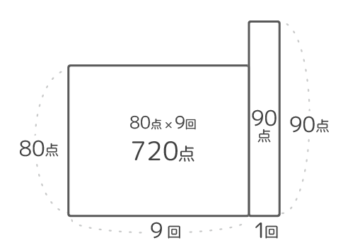
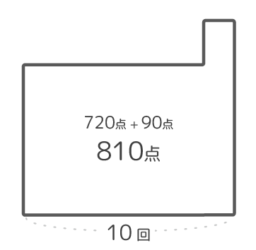
平らにならした高さが全回の平均で、810÷10で81点です。(図3)。
→
ならす
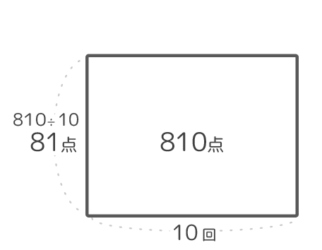
図の書き方の全体像を示します。
実際には最後の絵を書けばOK
難しい問題では、この図が約に立ちます。
簡単な問題
次のような回数が分かっている場合は図を書かなくても解けます。
1-1:サブタイトル
解説
五回全部の合計から四回目までの合計を引いたものが最後の点数です。
四回目までの合計点は70×4＝280点、五回全部の合計点は75×５＝375点なので、375－280＝95点が五回目のテストの点数と分かる。
図にするとこういう感じですね。
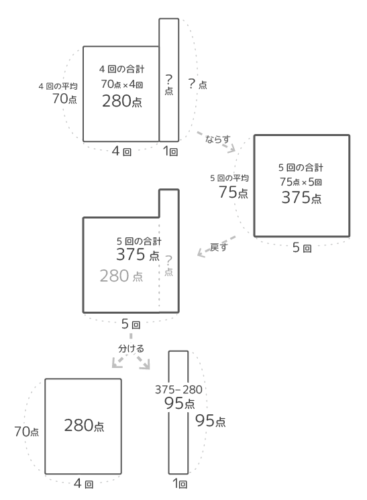
デコボコを一回ならして合計を出してから
もう一度デコボコに戻して
さらにもとの２つの面積図に分けています。
応用問題
次のように、回数が分からない場合は2つの面積図を重ねて解きます。「等しい面積を重ねると、はみ出た部分が等しくなる」のを利用します(詳しい説明は「面積図の重なり」を見て下さい。
1-1:サブタイトル
解説
今までのテストと最後のテストをくっつけた面積図を平らにならします(図1)
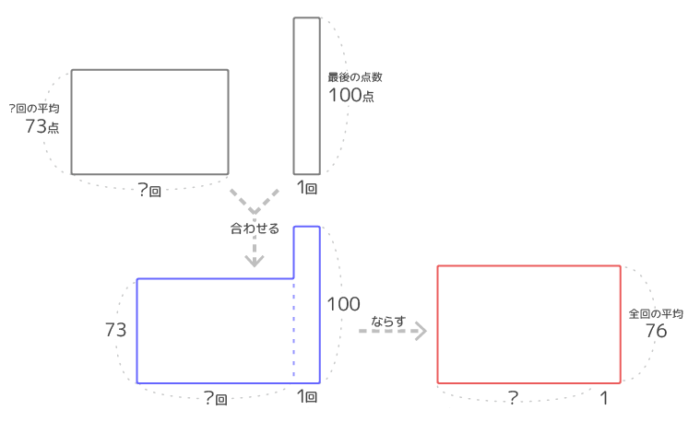
いつものパターンです
「ならす」前の凸凹の青い面積図と「ならした」後の赤い長方形の面積図を重ねると、2つの図は面積が等しいので「はみ出た部分(A,B)」の面積が等しくなります(図2)。
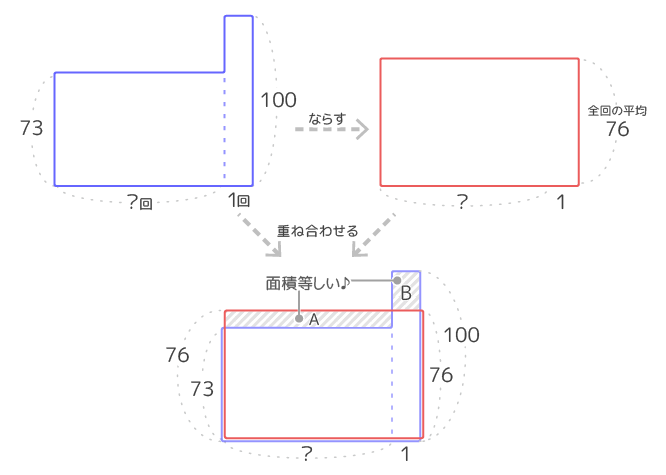
AとBは面積が等しくなる
Bはタテ24ヨコ1なので面積が1×24=24になり、Aの面積は同じく24でタテは3なのでヨコは24÷3=8と分かります。(図3)
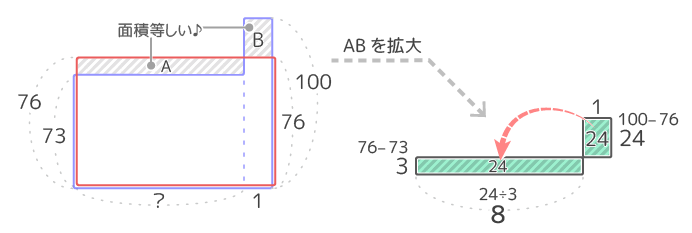
?が分かりました。
図の?=8なので、テストは全部で8+1=9回になります。
確認テスト(1)
何回かテストを受けて平均84点だったが、最後のテストで60点をとってしまい、全体の平均点が80点に下がってしまった。全部で何回テストを受けたか
→( 面積図を重ねて、等しい長方形を比べると、？×(84-80)=1×(80-60)なので、?=5回と分かる。テストは全部で6回 )
「2つのグループ」
クラスを男子と女子に、受験者を合格者と不合格者に、というように、集団を2つのグループに分け、集団全体とそれぞれグループの平均の関係を考える問題です。
公式/図の書き方
●グループAの合計=Aの平均×Aの人数
●グループBの合計=Bの平均×Bの人数
●全体の合計
=全体の平均×全体の人数(A+B)
=グループAの合計+グループBの合計
例題を解いてみます
1-1:2つのグループ(基本)
実際には最後の図を書けばOK
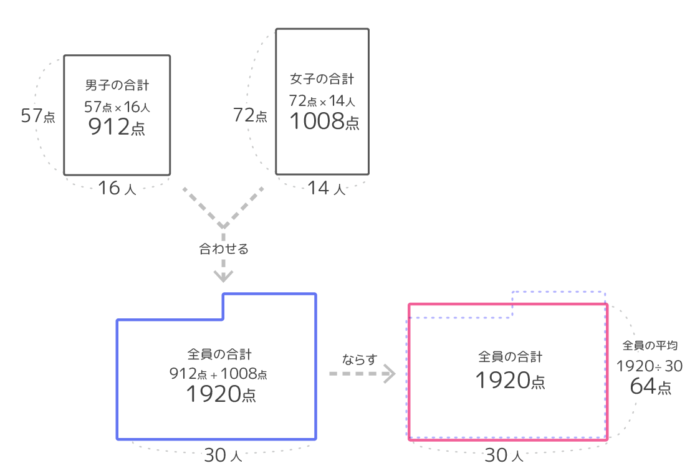
クラス全体の合計点=男子の合計点+女子の合計点です。男子の合計点＝57×16=912点、女子の合計点＝72×14=1008点なので、全体の合計点は912+1008=1920点と分かります(図1)
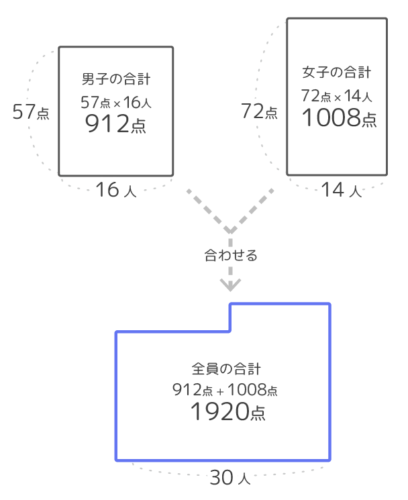
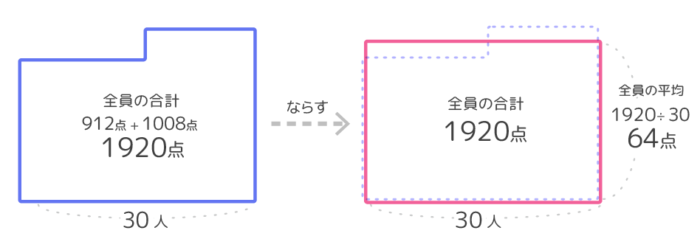
クラスの平均＝クラス全体の合計÷クラスの人数です。全体の合計＝1920、人数は16+14=30人なので、クラスの平均=1920÷30=64点です(図2)。
基本問題
人数や平均点が詳しく分かっている場合は面積図を使わなくても公式だけで解けることもあります。
2-1:2つのグループ(基本)
解説
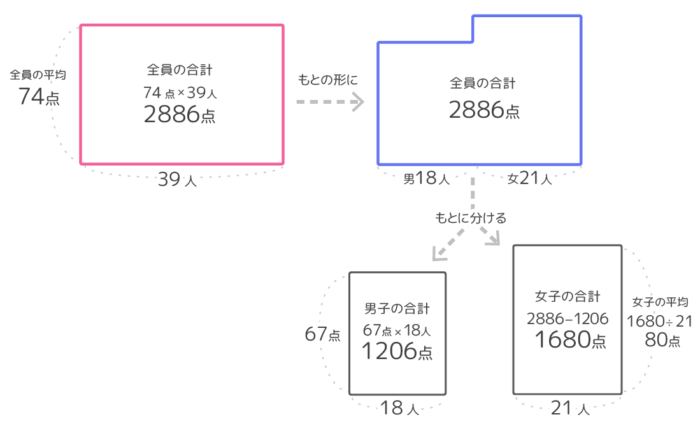
クラス全体の合計=(18+21)×74=2886点、男子の合計=18×67=1206点です。
そして女子の合計=全体の合計2886-男子の合計1206=1680なので、女子の平均は1680÷21=80点です。
さっきの問題と逆向きになっている。
確認テスト(2021.8.20作成中)
応用問題
数値が少なく、計算だけでは解けないな…と感じたらすぐに「重ね合わせ図」を書きます。
その1
2-2-1:2つのグループ(応用)
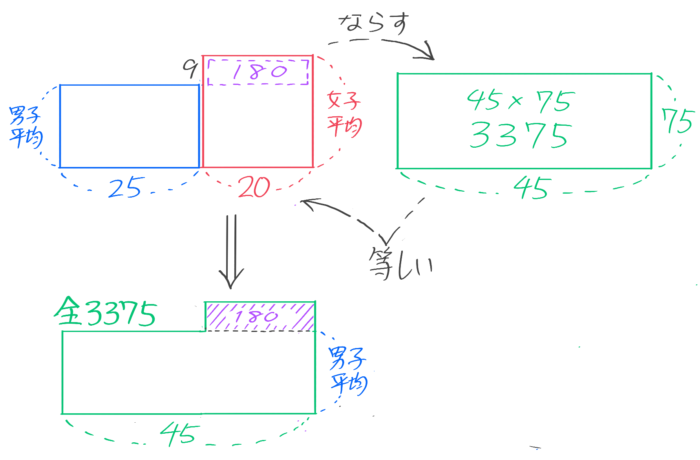
クラス全体の合計点=45×75=3375点なので、男女別の面積図をあわせたL字形の面積も3375点。
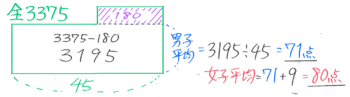
女子の高い部分は縦9横20なので面積は9×20=180点なので、残りの長方形の面積は3375-180=3195点
この長方形は横が45で縦が男子の平均点なので、男子の平均点は3195÷45=71点と分かる。
女子の平均は71+9で80点
その2
さらに具体的な得点が書いてない問題もあります。
2-2-2:2つのグループ(応用)
解説
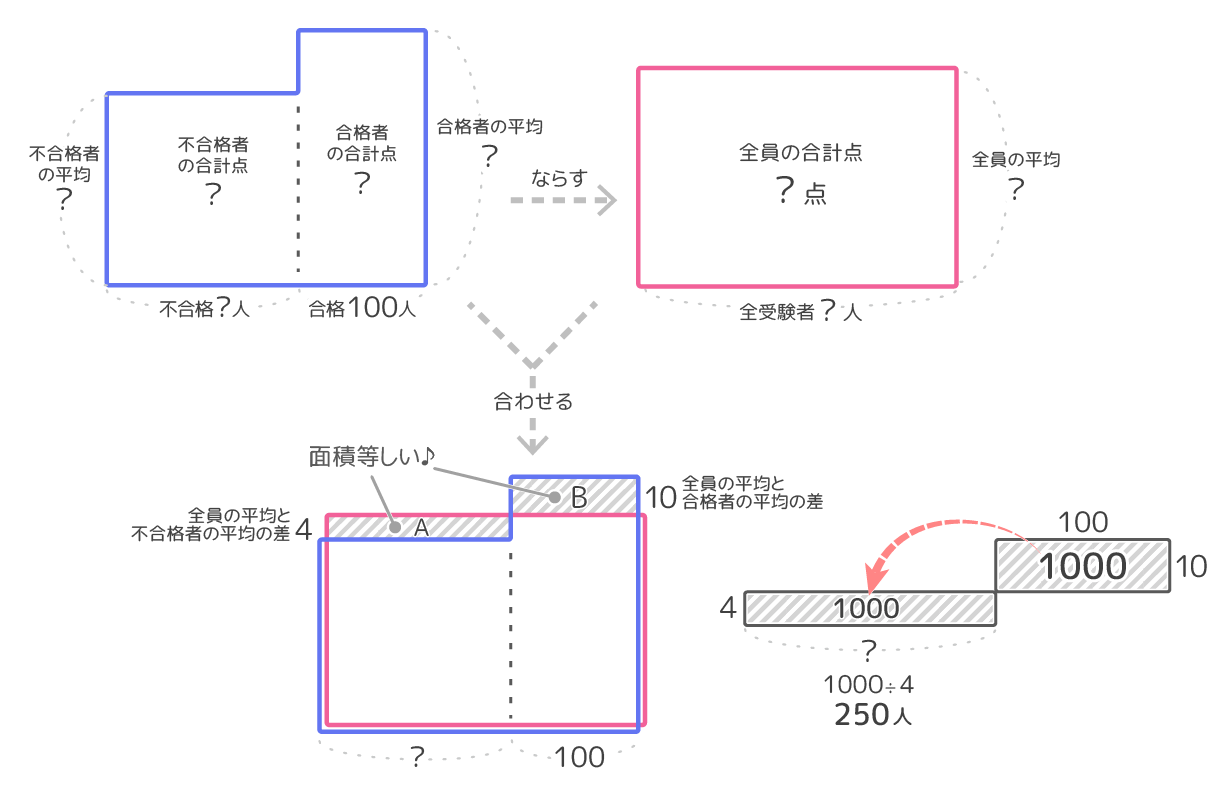
まず大きさはテキトーで良いので不合格者の面積図と合格者の面積図を合わせた図(青)とならした図(赤)を書きます。この二つの面積は当然同じです。
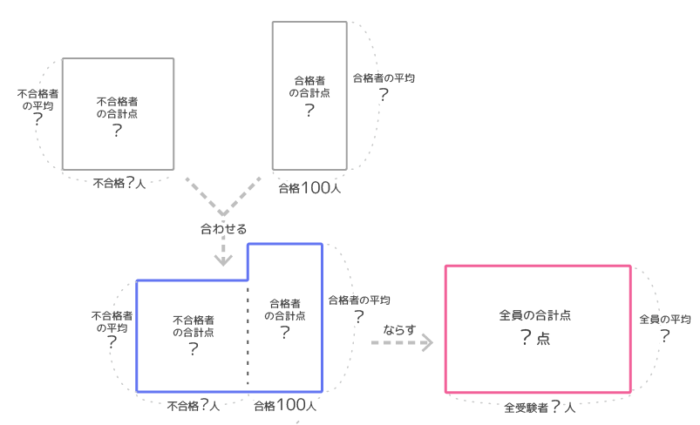
赤と青の面積は等しい
次に2つの面積図が重なった「重ね合わせ図」を作ります(図2)。等しい面積を重ねたので、はみ出たAとBの面積(斜線部分)は等しくなります。
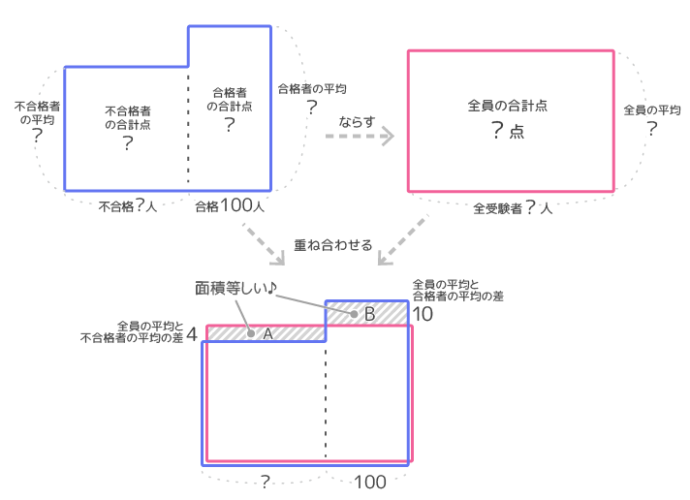
合格者の平均点は受験者全員の平均点より10点高いのでBのタテは10、不合格者の平均が合格者より14点低いのでAのタテは14-10=4です。また合格者の人数が100人なのでBのヨコは100です(図3)。
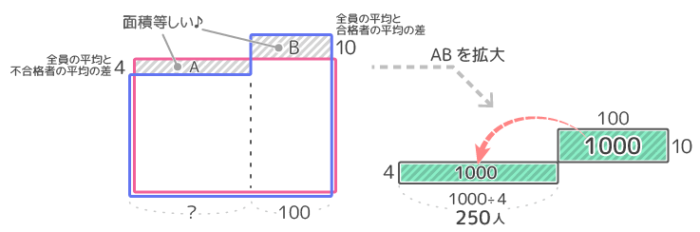
不合格者の人数が分かります
これでBの面積は10×100=1000と分かり、Aの面積も1000です。Aのタテが4なのでヨコは100÷4=250と分かります！これが不合格者の人数です(結局、平均点そのものは最後まで分かりません)。
以上より受験者の人数は、合格者100人+不合格者250人=350人です。
確認テスト(2021.8.20作成中)
その3(受験小4)
さらに分からないことが多い場合はさらに工夫が必要
その3(受験小5)
比(→参考記事「比の基本」)を習ったあとは工夫なしでも解ける
「段階式の価格」
例えば「ある印刷工場では、ポスターを印刷してもらうのに枚数によって値段が変わります。10枚までは1枚○円、11枚以上30枚までは1枚●円、31枚以上は1枚◉円で印刷してもらえます。1枚あたりの値段が◆円以下になるには何枚以上印刷してもらう必要がありますか？」という問題です。
例題1
チラシの印刷を工場に頼む。1枚目から100枚目までは1枚20円、101枚目から300枚目までは10円、301枚目からは更に安くなる。900枚印刷を注文したら1枚平均8円になった。301枚目からは1枚いくらだったか
→合計代金を順番に集計すると、(20円x100枚)+(10円x200枚)+(？円x600枚)=3000+(？x600)で、これを平均した8円を使って表すと8円x900枚=7200円になる。
つまり3000+(？x600)=7200 になるので、この逆算を解いて、？=7円と分かる
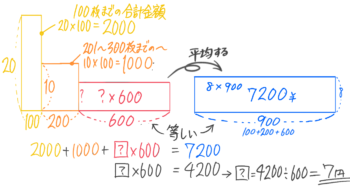
このように、多段階の価格の問題はグループ数が3つ以上になったつもりで面積図を書いて考えます。
練習問題をどうぞ
例題2
今度はパンフレットの印刷を工場に頼む。1冊目から100冊目までは1冊200円、101冊目から300冊目までは1冊150円、301冊目からは更に安くなる。700冊印刷を注文したら1冊平均100円になった。
(1)301冊目からは1冊いくらだったか
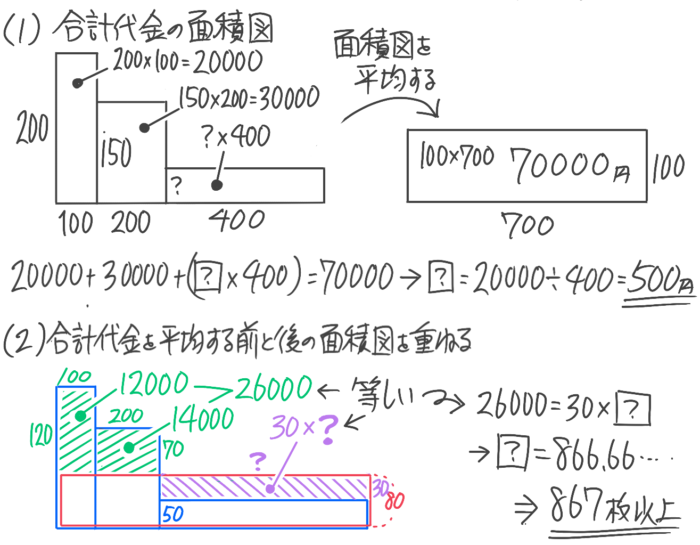
→700冊合計代金を2通りで表すと、(200×100)+(150×200)+(?x400)と700×100なので、
(200×100)+(150×200)+(?x400)=100×700
を逆算で解いて、→?=50円
(2)1冊平均80円より安くするには何冊以上注文すれば良いか
→ちょうど80円になるときの300冊を超える冊数を?として平均する前と後の面積図を重ねて、はみ出た部分の面積を求めると
A=(120×100)+(70×200)=26000、B=30x?
になり、
A=Bなので、26000=30x?
の逆算を解いて
?=26000÷30=866.66…円なので、867冊以上買えば良いと分かる
度数分布表
表を読み取って解く問題です。
度数分布表の使い方
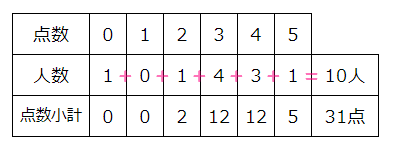
0点から5点までの点数がつくゲームを何人かでプレイした時の点数と人数を表にします(図1)
右から2列目は「4点を取ったのは3人」を意味する
右から2列目は「4点をとった人数が3人」をあらわしています。
この表を使って平均点を出してみましょう。
平均点=全員の合計点数÷人数なので、まず合計を求めます。
右から2列目の4点をとった3人の合計点(小計)は4×3=12点です。これを新しく作った三段目に書き込みます(図2)。
右から2列目の3人の小計は4×3=12点
同じように三段目を全て計算して、これらを合計すると全員の合計得点(総計)が31点と分かります！
列ごとの小計を合わせると全員の合計が出る
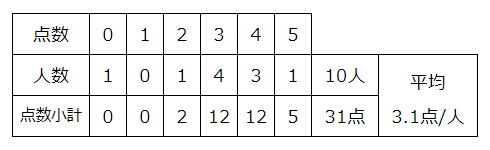
人数の合計は二段目を合計すれば10人と分かります(図4)。
二段目を合わせると人数の合計が出る
結局、平均点は合計31÷人数10=3.1点と分かります(図5)。
合計点(31)÷人数(10)で平均点(3.1)が出る
練習問題をどうぞ
9-1:度数分布表
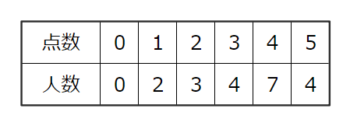爽くんのクラブで5点満点のゲームをした結果が右のような表になった。以下の問いに答えなさい解説
度数分布表をみたら、下に「点数の小計」欄、右に「人数・点数の合計」欄、右端に「平均」欄を書いてしまいましょう
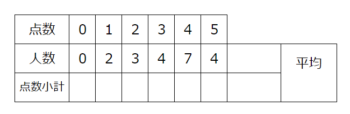
次に点数と人数をかけて点数の小計を出して…
それらを足すと合計点は68点になりました。
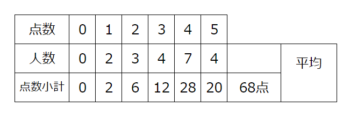
解説
さらに人数の合計を出して
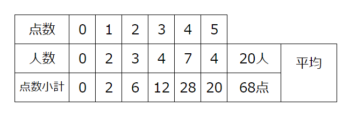
合計点÷合計人数で平均を出すと…
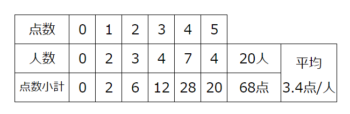
68÷20=3.4点と分かりました♪
度数分布表の見方が分かったと思うので、問題を解いてみましょう
基本問題(実質空欄が1個)
次の様に空欄がある度数分布表の問題を考えます。
9-2:度数分布表
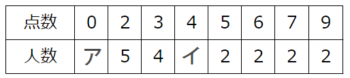22人の生徒が9点満点のテストを受けたところ全体の平均点はちょうど4点で、点数と人数は右の表のようになった。ア、イの人数を求めなさい人数に空欄が2つもありますが、合計人数と平均が分かっているので合計点数が分かりますね。それを利用します。
誘導形式で解いてみましょう。
9-2:度数分布表
22人の生徒が9点満点のテストを受けたところ全体の平均点はちょうど4点で、点数と人数は右の表のようになった。以下の問いに答えなさい。解説
さっきと同じように「下」と「右」に増築して、点数の小計を計算して書き込みます。さらに「0点」の人は何人いても点数小計は0点なので「0」と書き込めますね♪
また、問題文に書いてある合計人数と平均を書き込むと…
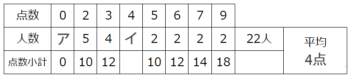
合計人数22x平均4で合計点数=88点と分かります。
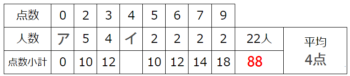
解説
ここで点数小計の空欄以外の点数を計算すると0+10+12+10+12+14+18=76点です。
ということは、空欄イの下の小計は88-76=12点と分かって
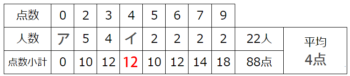
空欄イ=12÷4＝3人ですね!
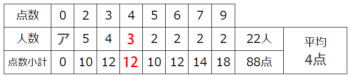
解説
空欄アは合計人数22から分かっている人数の合計5+4+3+2+2+2+2=20を引いて22-20=2人と分かります♪
分かりましたか？練習問題をどうぞ
9-2:度数分布表
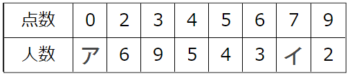34人の生徒が9点満点のテストを受けたところ全体の平均点はちょうど4点で、点数と人数は右の表のようになった。ア、イの人数を求めなさい図解
さっきと同じように「下」と「右」に増築して、点数の小計と合計人数と平均を書き込みます。
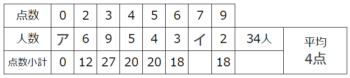
合計人数34x平均4で合計点数=136点と分かります。
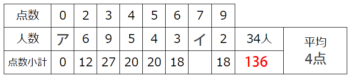
ここで点数小計の空欄以外の点数を計算すると115点なので、空欄イの下の小計は136-115=21点、空欄イ=21÷7＝3人です
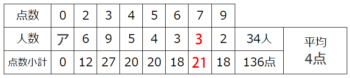
空欄アは合計人数34から分かっている人数の合計32を引いて2人と分かります♪
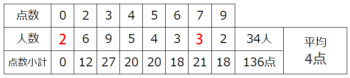
次は、もう少し難しい問題です
応用問題(空欄2個)
こんな問題です。
9-3:度数分布表
30人の生徒が100点満点のテストを受けたところ全体の平均点はちょうど58点で、点数と人数は上の表のようになった。ア、イの人数を求めなさい
今度は0点以外の2箇所が空欄になっています。このように空欄が(実質的にも)2つある問題は「つるかめ算」で解きます。
誘導式の例題で解いてみましょう
9-3:度数分布表(応用)
30人の生徒が100点満点のテストを受けたところ全体の平均点はちょうど58点で、点数と人数は上の表のようになった。以下の問いに答えなさい。
解説
例のごとく右と下に「増設」して小計と人数の合計を書き込みます。
解説
表の数字だけで分かるのはここまでですが、問題文に平均が58点とあり、これを使えば合計も58×30=1740と分かるので書き込みます。
解説
ここで、表の人数の合計は2+3+ア+8+イ+4=17+ア+イで、これが30になるのでア+イ=13人と分かります。
また表の点数小計を合計すると60+(40xア)+480+(80xイ)+400=940+(40xア)+(80xイ)で、これが1740になるので(40xア)+(80xイ)=800点と分かります。
つまり、「ア+イ=13人で(40xア)+(80xイ)=800」これは「40点の生徒と80点の生徒の人数の合計が13人で点数の合計が800点。40点の生徒は何人？」というつるかめ算と同じですね
解説
「40点の生徒と80点の生徒の人数の合計が13人で点数の合計が800点。40点の生徒は何人？」というつるかめ算を「面積図法」か「置き換え法」で解くと、ア={(80×13)-800}÷{80-40}=6人、イ=13-6=7人と分かります
完成した表は下のようになります。
分かりましたか？では練習問題をどうぞ
(2022.12.5作成中)
その他
●単元学習中の小4・小5には定評のある「算数の基本問題(小5)」(日能研)
●サッと復習したい小6受験生には「算数ベストチェック」(日能研)
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
そうちゃ受験に関する悩みはつきませんね。「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
自分だけで悩んでいると煮詰まってしまい、事態を改善できないかもしないこともあるでしょう…
そんな時は、講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインの授業/学習相談を受け付けているので、ご利用下さい。
この記事があなたの役に立てたなら嬉しいです!